پیش بینی سری زمانی به کمک شبکه عصبی در متلب
پیش بینی سری زمانی به کمک شبکه عصبی در متلب
خلاصه مبحث آموزشی :
پیشگویی سری زمانی یک مساله مهم کاربردی است که در بسیاری از زمینه ها نظیر پیش بینی وضع هوا، اقتصاد ، کنترل و … استفاده می شود .
در این پست ما از هوش مصنوعی (شبکه عصبی ، الگوریتم ژنتیک و الگوریتم فازی) برای مدل کردن سیستم ( مساله سری زمانی ) استفاده می کنیم و این روشها را با یکدیگر مقایسه می نماییم .
مساله سری زمانی به عنوان یک مساله شناسایی سیستم در نظر گرفته شده است ، درحالیکه ورودی های سیستم مقادیر گذشته سری زمانی اند و خروجی مطلوب مقدار آینده آن می باشد .
شبکه های عصبی backpropagation ، RBF (Radial Basis Functions) و PNN (polynomial neural network ) مورد بررسی قرار گرفته و سپس مدل پیشرفته PNN یعنی GBSON (genetic-based self organizing network) که تلفیقی از الگوریتم ژنتیک و شبکه عصبی PNN می باشد مورد بررسی قرار گرفته است .
در نهایت نیز یک مدل خاص از شبکه فازی برای تحلیل مورد استفاده قرار گرفته است .
مقدمه :
یک سری زمانی مجموعه ای از مشاهدات X(t) می باشد که هر کدام در یک زمان معین استخراج شده اند .
یک سری زمانی گسسته ، سری ای است که در زمانهای گسسته نمونه برداری شده است .
سری زمانی پیوسته سری ای است که با ثبت پیوسته مشاهدات در یک دوره زمانی بدست آمده است.[1]
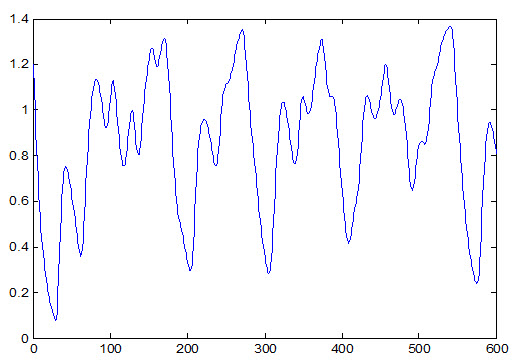
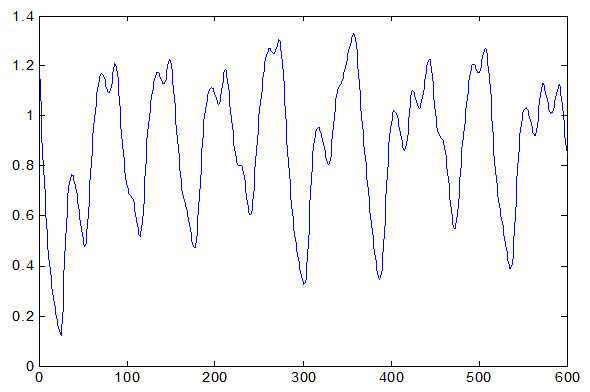
مثالی از یک سری زمانی در شکل (1) آمده است .
برای تحلیل داده های سری زمانی باید آن را به اجزایش تجزیه کرد .
هر جزء به عنوان یک فاکتور که در سری زمانی تاثیرگذار است در نظر گرفته میشود .
سه جزء اصلی سری زمانی مشخص شده اند .
1- Trend (تمایل) : گرایش به افزایش یا کاهش در دراز مدت را در یک سری زمانی نمایش می دهد .
2- Seasonality (فصلی) : رفتار تناوبی یک سری زمانی را در یک دوره معین از زمان نمایش می دهد .
3- Fluctuation (نوسان، تغییر) جزء بی قاعده سری زمانی می باشد . [1]
شکل (1) سری زمانی مکی گلاس
کاربردهای پیشگویی سری های زمانی را می توان در حوزه های تجارت ، اقتصاد ، کنترل موجودی ، پیش بینی وضع هوا ، پردازش سیگنال و کنترل و سایر زمینه ها پیدا کرد .
در این مقاله هوش مصنوعی برای حل مساله سری زمانی بکار گرفته شده است .
مساله سری زمانی به عنوان یک مساله شناسایی سیستم در نظر گرفته شده است ، درحالیکه ورودی های سیستم مقادیر گذشته سری زمانی اند و خروجی مطلوب مقدار آینده آن می باشد .
یک روش برای حل اینگونه مسائل استفاده از شبکه عصبی می باشد .
از میان شبکه های عصبی شبکه های عصبی TDNN و PNN بیشتر برای تشخیص سری زمانی بکار می روند در این مقاله شبکه های عصبی backpropagation ، RBF و PNN مورد بررسی قرار گرفته است و سپس برای رفع اشکالات آن از الگوریتم ژنتیک استفاده شده است و در نهایت نیز یک سیستم فازی برای حل مساله بکار گرفته شده است .
- سری زمانی مکی گلاس:
سری زمانی مکی گلاس با استفاده از فرمول زیر بدست می آید :
این سری برای T>17 حالت آشوبگونه و اغتشاشی از خود نشان می دهد و بنابراین در مسایل پیش بینی سری های زمانی چون پیش بینی نقاط بعدی این سری مشکل می شود از این سری جهت آزمایش استفاده می شود .
[2] نمونه این سری برای نقطه شروع 8/0 X=و 25T= به صورت زیر می شود :
2-شبکه های عصبی :
ایده شبکه عصبی در سال 1943 توسط مک کلوچ و پیتز ارایه شد.
این دو نفر مدل ساده نرون را ایجاد کردند که این نرون قابلیت ساخت دروازه های AND و OR را داشت .
سپس این مدل توسط دانشمندان دیگر توسعه پیدا کرد و از حالت تک نرون به شبکه ای از نرون ها توسعه یافت .
برای استفاده از یک شبکه عصبی باید ابتدا شبکه را تعلیم داد.
در سالهای گذشته ساختار های متنوعی برای شبکه های عصبی ارایه شده است.
شاید به مطالب زیر نیز علاقمند باشید:
- پیش بینی قیمت دلار و طلا با شبکه عصبی و الگوریتم ژنتیک در متلب
- شبیه سازی سیستم درایو کرامر استاتیکی با متلب
- سفارش شبیه سازی مقالات درس کنترل غیرخطی با متلب
- شناسایی سیستم غیر خطی ربات بازوی مسطح دو درجه آزادی توسط شبکه عصبی
- ماشین های القایی متقارن در متلب قسمت دوم
- آموزش دستورات متداول در متلب
- تشخیص فونم ها(لب خوانی) با SVM در متلب
- نوشتن و کار با فایل MEX. در متلب توسط زبان ++C
- سفارش شبیه سازی مقالات درس کنترل توان راکتیو
- تشخیص زن یا مرد بودن با پردازش تصویر در متلب و Avr
- انجام پروژه متلب با سایت متلبی
که از مهمترین آنها می توان به شبکه های بازگشتی و feedforward اشاره کرد .
برای این شبکه ها الگوریتم های مختلف تعلیم ارایه شده اند که می توان آنها را به دو دسته نظارتی و بدون ناظر تقسیم کرد .
از جمله کاربردهای شبکه های عصبی می توان به شناخت الگوهای مرئی (صوت،چهره،تصویر)، تقریب توابع، طبقه بندی، کنترل کننده ها و پیش بینی (وضع هوا،سریهای زمانی و…) اشاره کرد.
در بخش های بعد از شبکه های عصبی گوناگون برای پیش بینی سری زمانی استفاده شده است که ابتدا نوع شبکه ، ساختار آن و سپس الگوریتم تعلیم شبکه توضیح داده شده است .
2-1 شبکه عصبی RBF :
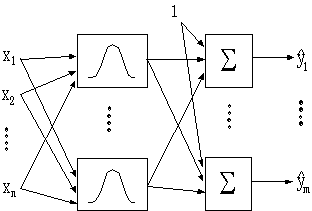
شبکه های عصبی بطور وسیعی در مسایل سری های زمانی و پیش بینی بکار می روند ساختارها و مدلهای گوناگونی از این شبکه ها برای این گونه مسایل طراحی شده اند یکی از این شبکه های عصبی شبکه عصبی توابع پایه ای شعاعی می باشد .
این شبکه یک لایه پنهان دارد که متشکل از نرونهایی است که تابع فعالیت آنها یک تابع گوسین ، چندجمله ای ، مکعبات و … می تواند باشد .
پارامترهای شبکه عصبی RBF وزنهای بین لایه پنهان و لایه خروجی ، مراکز توابع فعالیت وشعاع توابع فعالیت می باشند .
این شبکه برای مدلسازی سیستم سری زمتنی بکار برده شده است و نتایج آن در قسمت آزمایشات با بقیه شبکه ها مقایسه شده است .
الگوریتم تعلیم شبکه عصبی RBF :
ورودی الگوریتم:
حداکثر خطای مورد نظر ، الگوهای تعلیم و شعاع نرون های لایه مخفی
مراحل:
- l=1 تعداد یک نرون در لایه مخفی
- یک الگوی تعلیم را بطور تصادفی انتخاب کرده و آن را به عنوان مرکز نرون l قرار می دهیم .
- محاسبه وزنهای لایه دوم
- خطای شبکه به تمامی الگوهای تعلیم را بدست می آوریم
- اگر خطا از خطای مورد نظر کمتر است توقف کن
- در غیر اینصورت l=l+1 به گام 2 برگرد .
مزایا و معایب شبکه RBF :
- اشکالات RBF :
- این شبکه برای الگوهای تعلیم خطای نسبتا کمی دارد ولی برای الگوهای تست خطا زیاد می شود
- شعاع r باید ابتدا تعیین شود که با تغییر r وزنها خیلی تغییر می کنند .
هر چه تعداد نرون ها بیشتر شود تعمیم پذیری شبکه (جواب آن به داده های تست) بدتر می شود .
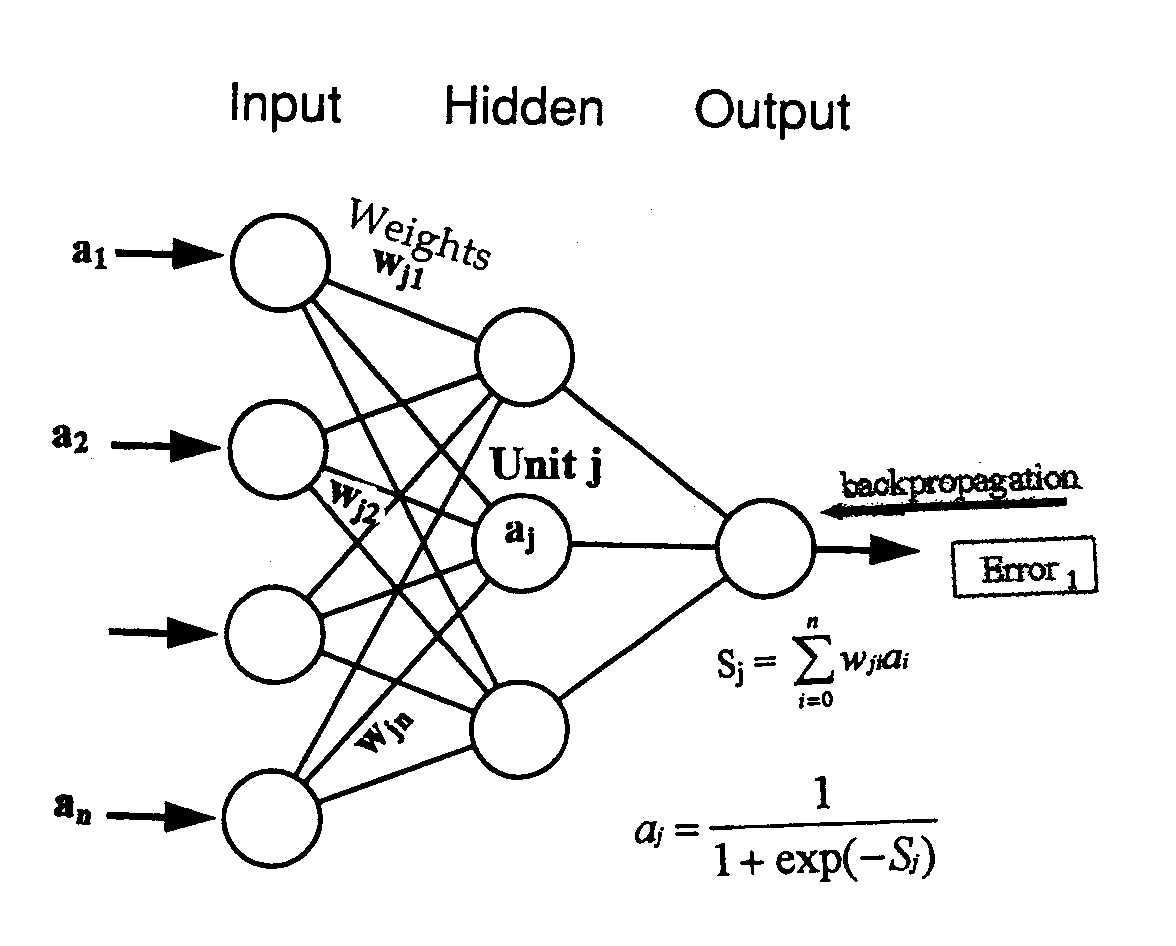
2-2- شبکه عصبی Backpropagation :
- الگوریتم شبکه عصبی Backpropagation :
الگوریتم دسته ای :
- وزنهای اولیه شبکه را در مقادیر تصادفی کوچک قرار می دهیم .
- برای تمام الگوهای تعلیم P=1,2,…,p مراحل انتشار مستقیم و معکوس زیر را تکرار کن
2-1) انتشار مستقیم : ورودی Xp را به شبکه اعمال و تمام خروجیها و خالص ورودیها (net)را حساب کن .
2-2) انتشار معکوس : ابتدا خطا را حساب می کنیم سپس را حساب مي كنيم .
يعنی از لايه خروجي شروع كرده و اين محاسبات را انجام مي دهيم و براي لايه های دیگر نيز محاسبات را به صورت زير انجام مي دهیم:
2-3) مقادیر را ذخیره می کنیم .
2-4) حساسیت نسبت به تک تک الگوها را حساب کرده و همه را با هم جمع می کنیم
- وزنهای جدید را محاسبه می کنیم :
- به قدم 2 برگرد تا شرط پایان برقرار شود. (ساده ترین شرط توقف تعداد تکرار الگوریتم یا رسیدن الگوریتم به یکخطای مطلوب است )
الگوریتم تکراری نیز دقیقا مانند این روش است با این تفاوت که بعد از بدست آوردن خطای یک الگو وزنها را عوض می کنیم .
البته الگوریتم تکراری همگرایی اش سریعتر است .
نظريه فازی برای اولين بار در سال 1960 توسط استاد ايرانی دانشگاه کاليفرنيا، پروفسور لطفی زاده مطرح شد.
درکنترل فازی برای هر پديده يک تابع در نظر مي گيرند که ميزان تعلق آن را به يک مجموعه بيان مي کند .
در این شيوه سه مرحله وجود دارد.
ابتدا مرحله فازی سازی است که مرحله تعريف مجموعه های فازی برای متغيرهای ورودی وخروجی است.
برای تعريف اين مجموعه های فازی، بايد دانش اوليه ای از دامنه تعريف هر کدام از اين متغيرها داشته باشيم .
در مرحله بعد يا مرحله استنتاج،تعدادی قاعده فازی بوجود مي آوريم و در مرحله آخر که مرحله غيرفازی سازی نام دارد،با توجه به مقادیری که در مرحله استنتاج بدست آمده است مقداری حقيقی برای خروجی بدست مي آوريم
الگوریتم تعليم (روش جدول جستجو):
- مجموعه های فازیی را تعیین می کنیم که زوج های ورودی – خروجی را پوشش دهد
- از روی هر زوج ورودی – خروجی یک قاعده تولید می کنیم.
- یک درجه به هر قاعده تولید شده در گام دوم نسبت می دهیم و از بین قواعد متضاد قاعده ای که بالاترین درجه را دارا می باشد نگه می داریم. که به این ترتیب تعداد قواعد کاهش می یابد.
- پایگاه قواعد فازی را ایجاد می کنیم.
- ساخت سیستم فازی بر اساس پایگاه قواعد.
این طراحی بر اساس سیستم فازی با موتور استنتاج ضرب، فازی ساز منفرد و غیر فازی ساز میانگین مراکز به صورت زیر خواهد بود:
اشکالات سیستم (روش جدول جستجو):
- در این روش توابع تعلق ثابت اند و به زوج های ورودی خروجی بستگی ندارند . بدین معنی که توابع تعلق با توجه به زوج های ورودی خروجی به طور بهینه ای به دست نمی آیند.
- پایگاه قواعد فازی در این روش ممکن است کامل نباشد که در نتیجه سیستم پاسخ خوبی به داده های تست نمی دهد.
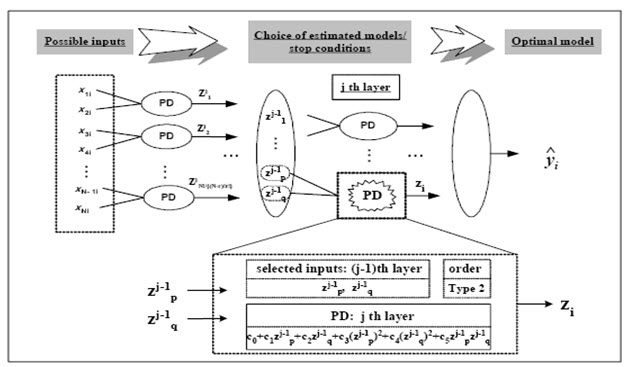
GMDH (Group Method Data Handling) :
در اواخر دهه 1960 توسط Ivakhnenko به عنوان وسیله ای برای شناسایی ارتباطات غیرخطی بین متغیرهای ورودی و خروجی ارائه شد .
الگوریتم GMDH یک ساختار بهینه از مدل را توسط نسلهای موفق توصیفات جزئی (PD) داده که به عنوان چندجمله ای های درجه دوم با دو ورودی در نظر گرفته شده اند را ارائه می کند .
البته این الگوریتم مشکلاتی نیز دارد که بعدها این مشکلات توسط ارائه شبکه عصبی چند جمله ای تا حدودی مرتفع شده است .
تابع انتقال هرPD از فرمول زیر بدست می آید :
اشکالات GMDH :
1- گرایش به ایجاد چندجمله ای کاملا پیچیده برای سیستمهای نسبتا ساده دارد .
2- به علت ساختار عمومی GMDH ( چند جمله ای دو متغیره درجه دوم ) ، گرایش به ایجاد یک شبکه (مدل) کاملا پیچیده وقتی که برای سیستمهای غیرخطی مراتب بالاتر بکار می رود دارد .
3- برای سیستمهای کمتر از سه ورودی ساختار مناسبی ندارد .
راه حل :
استفاده از شبکه عصبی چندجمله ای در این روش
2-3- شبکه عصبی PNN (Polynomial neural network):
شبکه عصبی چندجمله ای الگوریتم جدیدی است که قابلیت انعطاف بسیار زیادی دارد به طوریکه هر گره در این شبکه هم از لحاظ تعداد ورودی (حداکثر سه ورودی) و هم از لحاظ تابع انتقال آن (حداکثر سه ورودی) می تواند متفاوت باشد .
مرتبه چندجمله ای ها در هر گره شبکه می تواند متفاوت (خطی ، درجه دوم ومکعب)باشد .
معماری این شبکه از ابتدا ثابت نیست (هم ساختار و هم پارامترهای شبکه ) اما کاملا بهینه می شود ، بطور مثال تعداد لایه ها می تواند با اضافه شدن لایه جدید اگر لازم باشد افزایش یابد .
الگوریتمهای آموزش شبکههای چندجملهای
-
- Group Method of Data Handling (GMDH)
- Polynomial Network Training Routine (PNETTR)
- Algorithm for Synthesis of Polynomial Network (ASPN)
- همگی توسط A.G.Ivakhnenko معرفی شدهاند.
- انجام پروژه متلب با سایت متلبی
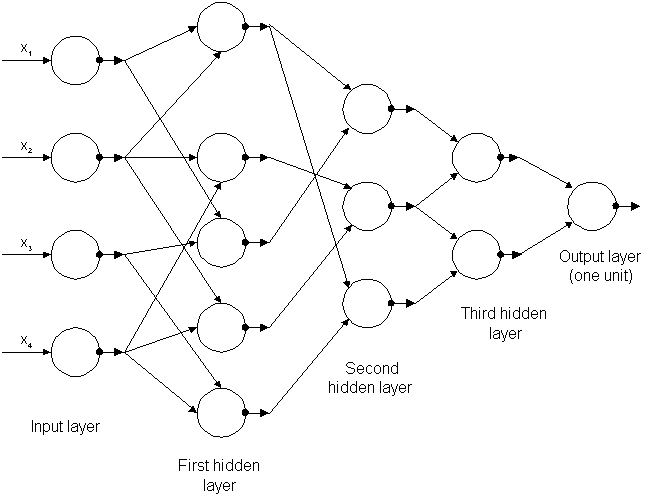
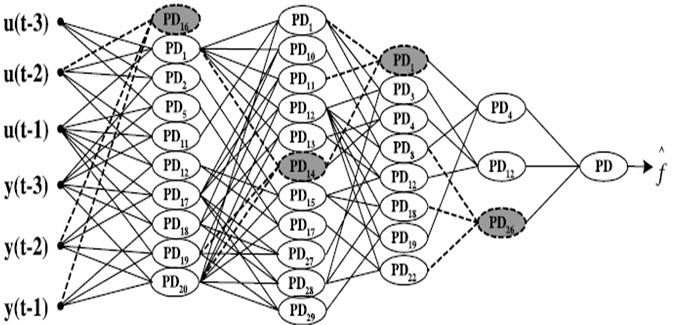
ساختار کلی شبکه عصبی PNN به صورت شماتیک :
الگوریتم تعلیم شبکه عصبیPNN :
ابتدا داده ها را به صورت زیر در می آوریم :
برای محاسبه خروجی تخمینی ، ما برای هر جفت ورودی یک PD تشکیل می دهیم. تعداد PD ها بر اساس تعداد ورودیها می باشد .
مثلا اگر 4 ورودی داشته باشیم تعداد آنها 6 عدد می شود . پارامترهای مدل از روی حداقل خطای داده های آموزش بدست می آیند .
بعلاوه ما بهترین مدل را برای تشکیل لایه اول انتخاب می کنیم.
در نهایت ما PD های جدید را از روی متغیرهای میانه (Zm ها) که در تکرار جدید واقع شده اند ایجاد می کنیم .
سپس ما یک جفت از متغیرهای ورودی جدید را گرفته و عملیات را روی آن انجام می دهیم تا زمانیکه به معیار توقف برسیم .
هنگامی که لایه پایانی ساخته شد گره با بهترین عملکرد به عنوان خروجی در نظر گرفته می شود . بقیه گره های آن لایه حذف می شوند . این عملیات در لایه های قبلی تا لایه اول انجام می شود .
مراحل طراحی شبکه PNN :
- ابتدا متغیرهای ورودی را نرمالیزه کرده و مطابق جدول زیر آنها را تقسیم می کنیم .
|
X متغیرهای ورودی |
خروجیY |
|
x1 x2 ….. xN |
Y |
2-داده ها را به دو دسته تست و آموزش تقسیم می کنیم :
|
X |
Y |
| x11 x21 ….. xN1 x12 x22 ….. xN2 . . . x1ntr x2ntr ….. xNntr |
Y1 Y2 . . . Yntr |
| x11 x21 ….. xN1 x12 x22 ….. xN2 . . . x1nte x2nte ….. xNnte |
Y1 Y2 . . . Ynte |
n=nte+ntr داده آموزش برای تشکیل مدل PNN استفاده می شود .
(محاسبه ثوابت هر PD گرههای موجود در هر لایه)سپس داده تست برای ارزیابی مدل PNN استفاده می شود .
شاید به مطالب زیر نیز علاقمند باشید:
- مدل فرایند گاورنر 4درجه آزادی جهت کنترل سرعت توربین
- آموزش نحوه اجرای برنامه متلب
- پیش بینی قیمت دلار و طلا با شبکه عصبی و الگوریتم ژنتیک در متلب
- فعالیت های متلبی در حوزه انجام شبیه سازی با Matlab
- چگونه تخفیف 25درصد از متلبی بگیریم
- انتخاب یک ساختار برای PNN :
ساختار PNN براساس تعداد ورودی ها و مرتبه PD هر لایه انتخاب می شود .
دو نوع ساختار PNN بنیادی و PNN اصلاح شده ، متمایز شده اند . هر کدام از آنها به دو دسته تقسیم می شوند : جدول زیر این دو ساختار را نشان می دهد .
- تعیین تعداد متغیرهای ورودی و مرتبه چندجمله ای تشکیل دهنده PD :
ما متغیرهای ورودی یک گره را ازبین N متغیر ورودی انتخاب می کنیم .
تعداد کل PD های لایه حاضر بر طبق تعداد متغیرهای ورودی انتخاب شده از گره های لایه قبل تغییر می کند .
در نتیجه تعداد گرهها برابر N!/(N-r)!r! می شود که r تعداد متغیرهای ورودی انتخاب شده است.
- تخمین ثوابت PD :
از رابطه زیر محاسبه می شوند :
i شماره گره ، k شماره داده ntr تعداد داده آموزش ، n تعداد ورودیهای انتخابی ، m ماکسیمم درجه، n’ تعداد ثوابت تخمینی .
5- انتخاب PD با بهترین عملکرد :
هر PD توسط داده های آموزش و تست تخمین زده شده و ارزیابی می شود .
سپس ما اینها را باهم مقایسه کرده و PD هایی را که عملکرد بهتری داشته اند جدا می کنیم .
معمولا ما یک تعداد W از قبل تعیین شده از این PD ها را انتخاب می کنیم .
6-چک کردن شرط توقف :
الف- اگر خطای مرحله بعدی از خطای مرحله قبلی بزرگتر باشد .
ب-اگر تعداد لایه ها به تعداد از قبل تعیین شده توسط کاربر برسد.
7- انتخاب متغیرهای جدید برای لایه بعد.
خروجی های لایه قبل را به عنوان ورودی لایه جدید در نظر می گیریم.
مراحل 4 تا 7 را تا رسیدن به شرط توقف تکرار می کنیم .
همان طور که دیده می شود ضرایب این شبکه به وسیله فرمول زیر به دست می آیند :
این ضرایب به صورت زیر بدست می آیند ، همانطورکه می دانیم خروجی به صورت زیر بدست می آید:
حال برای محاسبه ضرایب مراحل زیر طی می شوند :
هر چند این فرمول ضرایبی را می دهد که خطا را کاهش می دهد اما این خطا می نیمم خطا نیست و با تغییر ضرایب می توان به جوابهای بهتری دست یافت .
اما این ضرایب را چگونه می توان از میان انبوه اعداد یافت؟
یکی از راه حلها استفاده از الگوریتم ژنتیک برای بدست آوردن بهترین ضرایب جهت کاهش خطا می باشد .
حال به صورت زیر از الگوریتم ژنتیک برای بهبود ضرایب در شبکه عصبی PNN استفاده شده است :
الف – ورودیهای لایه اول را همان متغیرهای مستقل داده ورودی در نظر می گیریم .
ب – خروجی های هر لایه بهترین گره های بدست آمده توسط الگوریتم ژنتیک هستند که اینها خود ورودی های لایه بعد می شوند .
ج – ضرایب هر گره را به صورت جمعیت اولیه برای الگوریتم ژنتیک در نظر می گیریم و الگوریتم ژنتیک را برای یافتن بهترین ضرایب بکار می بریم .
پس از بدست آوردن بهترین ضرایب این گره های با بهترین ضرایب را از بقیه جدا می کنیم و ورودی را به اینها می دهیم تا خروجی گره های لایه اول بدست آید .
- انجام پروژه متلب با سایت متلبی
این خروجی ها را به عنوان ورودی لایه بعدی در نظر می گیریم .
این کار را تا زمانی که به خطای مورد نظر برسیم ادامه می دهیم .
روشی که در این تحقیق استفاده شده است به صورت زیر می باشد :
ابتدا سه گره را در نظر می گیریم .
سپس برای هر گره به ترتیب 20 جمعیت در نظر می گیریم .
هر فرد به صورت زیر در نظر گرفته می شود .
هر فرد را به عنوان یک رشته 128 بیتی در نظر می گیریم که هر 32 بیت آن مربوط به یک ضریب می باشد .
در اینجا 4 ضریب در نظر گرفته شده است .
بیت اول از هر 32 بیت به عنوان بیت علامت در نظر گرفته می شود (+ یا – ) .
2 بیت بعدی برای قسمت صحیح ضریب و مابقی بیت ها برای قسمت اعشاری در نظر گرفته می شوند .
حال ابتدا با استفاده از روش تورنمنت (q=6) 6 فرد را انتخاب کرده دو نفر را به عنوان والد انتخاب می کنیم .
سپس عمل تقاطع را با ضریب Pc=0.95 و بعد آن عمل جهش را با ضریب Pm=.05 انجام می دهیم ، تا دو فرزند جدید ایجاد شوند . این کار را تا زمان تولید P=20 فرزند تکرار می کنیم.
حال با استفاده از روش Elitism (نخبه گرایی) بهترین فرد نسل قبل را نیز به نسل جدید منتقل می کنیم . این کار را به تعداد نسل های لازم (3500 نسل ) تکرار می کنیم .
سپس بهترین فرد نسل آخر را به عنوان ضرایب برای این گره انتخاب میکنیم و به گره بعد می رویم .
بعد از این که لایه اول تمام شد اگر به شرط توقف رسیدیم می ایستیم در غیر اینصورت به لایه بعد می رویم .
خروجی های لایه اول را به عنوان ورودی لایه بعد در نظر گرفته و همین مراحل را برای لایه بعد تا زمان رسیدن به پاسخ مطلوب ادامه می دهیم .
در کلیه محاسبات برای شبکه ها تعداد ورودی ها را 3 در نظر گرفته ایم . یعنی جمله چهارم را بر اساس سه جمله قبل مشخص می کنیم .
– نتایج بدست آمده از شبکه BP :
در اینجا از شبکه عصبی BP با ساختار 3L 15N 1L استفاده شده است که نتایج زیر بدست آمده است.
نمودار تعداد تکرار اموزش شبکه وخطای بدست امده برای داده ها:
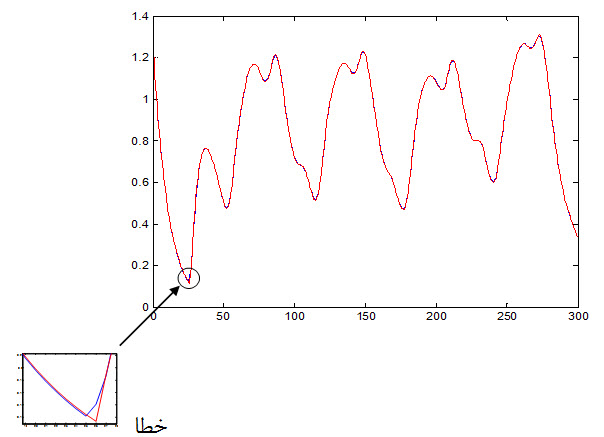
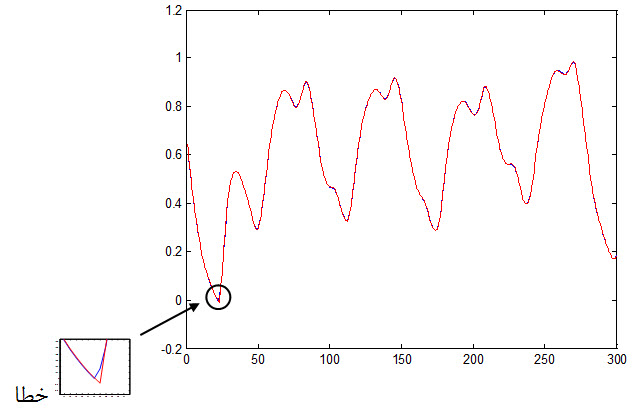
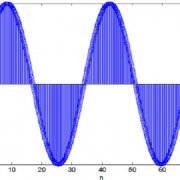
نمودار جواب مطلوب و جواب شبکه به داده آموزش که به صورت زیر می باشد ولی به علت خطای بسیار ناچیز با چشم قابل مشاهده نیست .
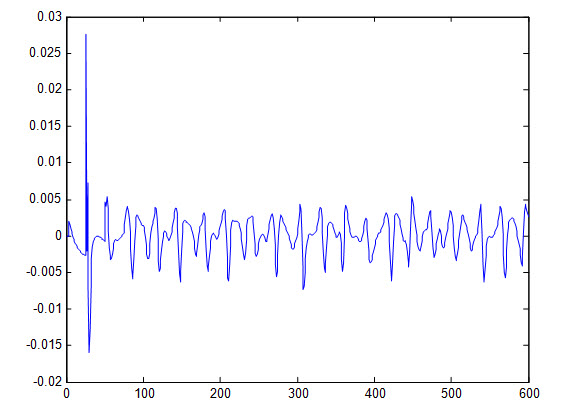
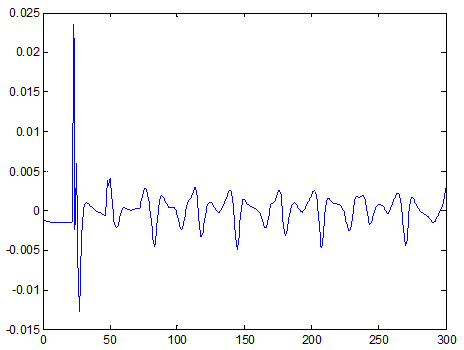
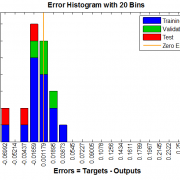
خطای بدست آمده از داده آموزش:
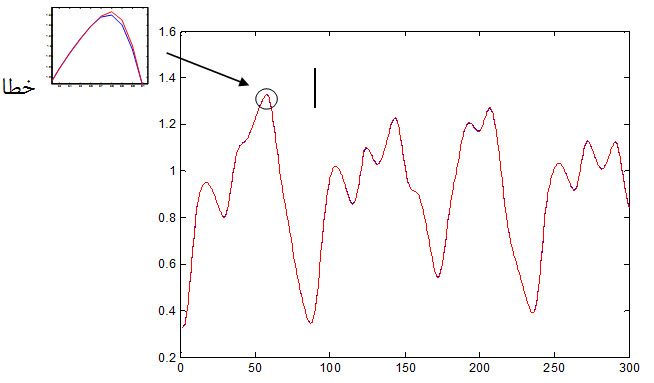
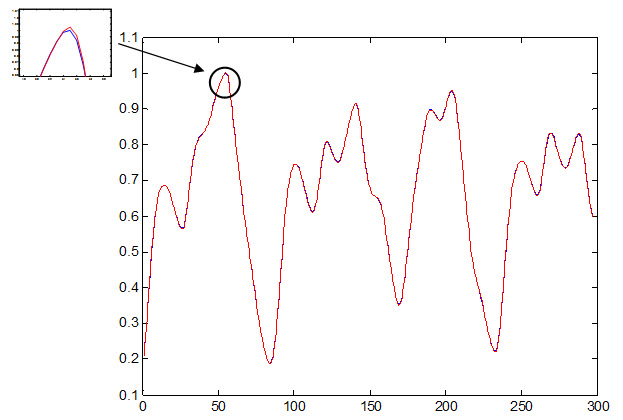
نمودار جواب مطلوب و جواب شبکه به داده تست که به صورت زیر می باشد ولی به علت خطای بسیار ناچیز با چشم قابل مشاهده نیست .
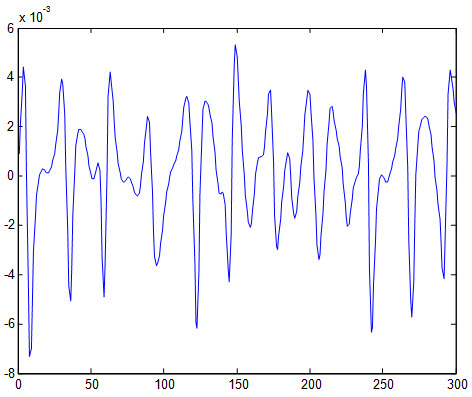
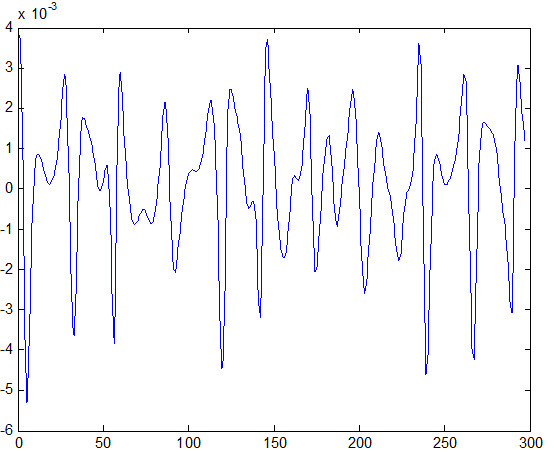
خطای داده تست:
2- نتایج بدست آمده از شبکه RBF:
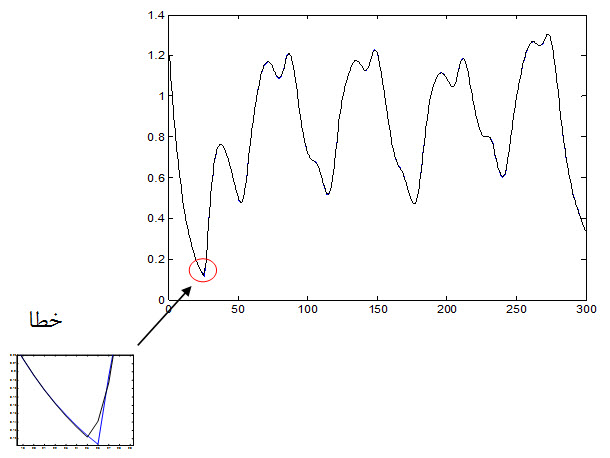
شکل زیر داده آموزش مطلوب و پاسخ شبکه به داده های ورودی را نشان می دهد.
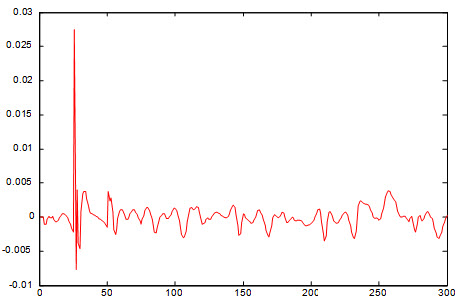
شکل زیر خطای شبکه نسبت به داده آموزش را نشان می دهد :
نمودار جواب مطلوب و جواب شبکه RBF به داده تست که به صورت زیر می باشد :
خطای داده تست:
3- نتایج بدست آمده از سیستم فازی (جدول جستجو):
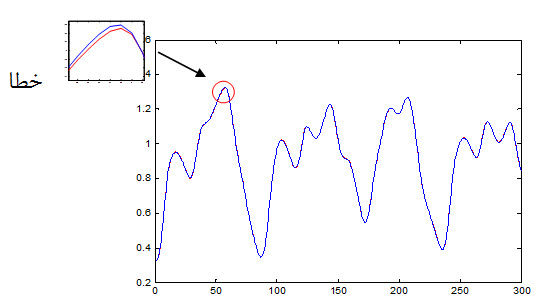
شکل زیر داده آموزش مطلوب و پاسخ سیستم به داده های ورودی را نشان می دهد:
به علت خطای زیاد سیستم فازی با چشم نیز این خطا قابل مشاهده است .
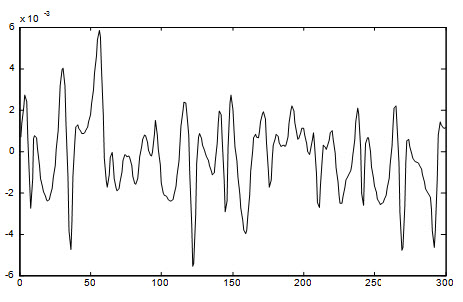
شکل زیر خطای سیستم نسبت به داده آموزش را نشان می دهد : 1246/0 = Etr
نمودار جواب مطلوب و جواب سیستم فازی به داده تست که به صورت زیر می باشد :
هر چند که در داده های تست سیستم فازی بهتر عمل کرده است اما باز هم خطا نسبت به شبکه عصبی زیاد است.
خطای داده تست: 032/0Ete =
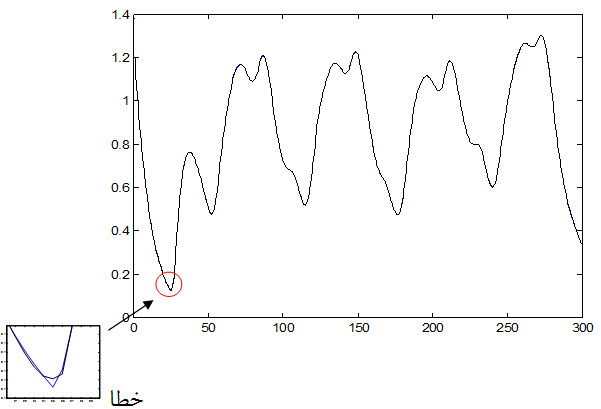
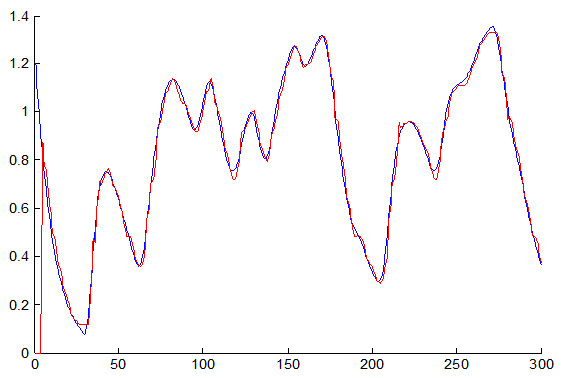
4- نتایج بدست آمده از شبکه عصبی PNN :
شکل زیر داده آموزش مطلوب و پاسخ سیستم به داده های ورودی را نشان می دهد:
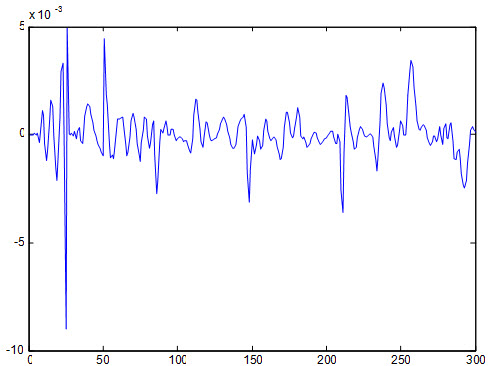
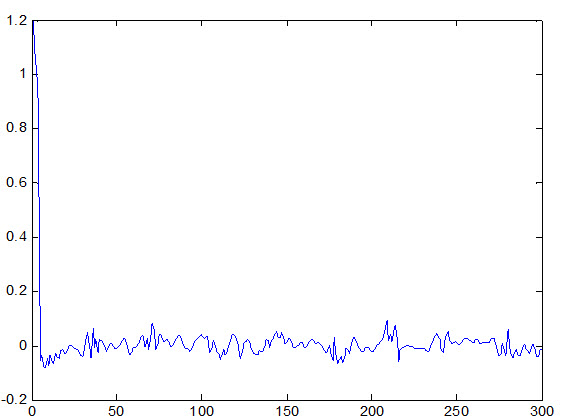
شکل زیر خطای شبکه نسبت به داده آموزش را نشان می دهد :
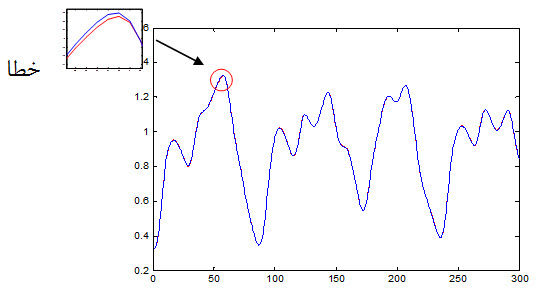
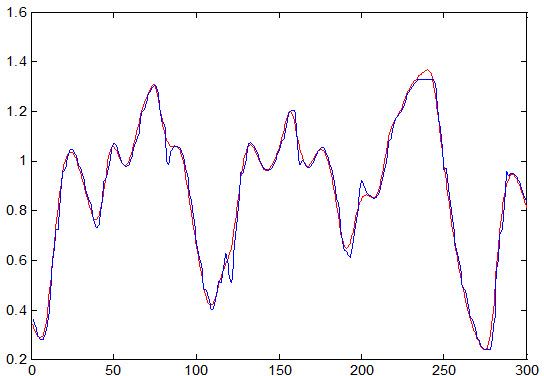
نمودار جواب مطلوب و جواب شبکه PNN به داده تست که به صورت زیر می باشد :
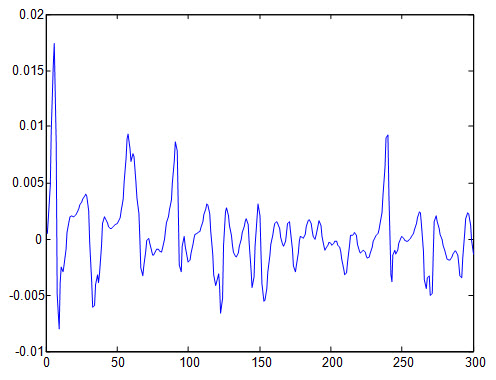
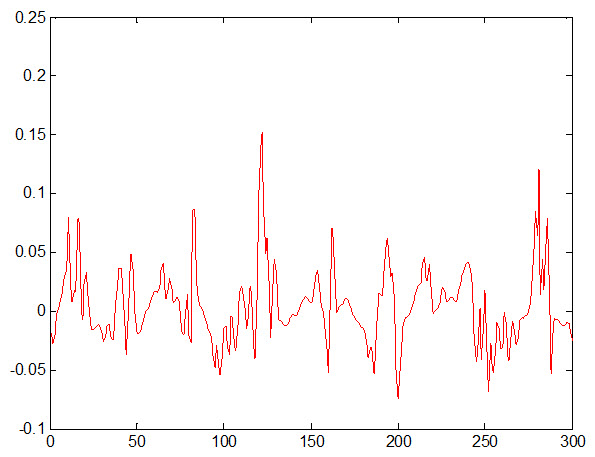
شکل زیر خطای شبکه نسبت به داده آموزش را نشان می دهد :
5- نتایج بدست آمده از شبکه عصبی GBSON:
شکل اصلی و شکل پیش بینی شده داده آموزش :
شکل زیر خطای شبکه نسبت به داده آموزش را نشان می دهد :
نمودار جواب مطلوب و جواب شبکه GBSON به داده تست :
خطای داده تست :
مقایسه عملکرد شبکه ها در پیش بینی سری زمانی
| شبکه عصبی ژنتیک GBSON | شبکه عصبی PNN | شبکه عصبی RBF | شبکه عصبی BP | سیستم فازی | |
| 0023/0 | 00245/0 | 0011/0 | 0023/0 | 1246/0 | خطای داده آموزش |
| 0016/0 | 00186/0 | 0031/0 | 0017/0 | 032/0 | خطای داده تست |
| 00195/0 | 0022/0 | 0022/0 | 002/0 | 0639/0 | میانگین خطا |
نتیجه گیری :
از لحاظ سرعت شبکه عصبی PNN بهترین سرعت را چه در مرحله آموزش و چه در مرحله تست دارا می باشد .
بهترین پاسخ برای داده آموزش را شبکه عصبی RBF دارا می باشد و بدترین پاسخ مربوط به سیستم فازی می باشد .
بهترین پاسخ برای داده تست را شبکه عصبی- ژنتیک GBSON دارا می باشد و بدترین پاسخ مربوط به سیستم فازی می باشد . البته سرعت آموزش شبکه GBSON بسیار پایین است .
از لحاظ میانگین خطا نسبت به داده تست و آموزش نیز بهترین پاسخ مربوط به شبکه GBSON می باشد .
MFILE ها :
1- برنامه نوشته شده برای شبکه BP در مطلب :
clc
clear
load(‘E:\shenasaey projeh\x’);load(‘E:\shenasaey projeh\xtr’);load(‘E:\shenasaey projeh\xte’)
load(‘E:\shenasaey projeh\ytr’);load(‘E:\shenasaey projeh\yte’);
xtr=xtr’;
ytr=ytr’;
xte=xte’;
net.trainParam.epochs = 500;
net.trainParam.goal = 0;
net.performFcn=’mse’;
net = newff(xtr,ytr,[15]);
net = train(net,xtr,ytr);
y = sim(net,xtr);
y=[x(1:3) y];
figure(1)
plot(y)
hold on
plot(x(1:300),’k’)
etr=(x(1:300)-y).^2;
figure(2)
plot(x(1:300)-y,’r’)
Etr=sqrt(sum(etr)/300)
figure(3)
yte=sim(net,xte);
plot(yte,’r’)
hold on
plot(x(301:600),’b’)
e=(x(301:600)-yte).^2;
figure(4)
plot(x(301:600)-yte,’k’)
E=sqrt(sum(e)/300)
2- برنامه نوشته شده برای شبکه RBF :
clc
clear
load(‘E:\shenasaey projeh\x’)
load(‘E:\shenasaey projeh\xte’)
load(‘E:\shenasaey projeh\xtr’)
load(‘E:\shenasaey projeh\yte’)
load(‘E:\shenasaey projeh\ytr’)
xtr=xtr’;
ytr=ytr’;
xte=xte’;
yte=yte’;
net=newrbe(xtr,ytr);
Y=[];
for i=1:297
Y =[Y sim(net,xtr(:,i))];
end
Y=[x(1,1:3) Y];
plot(x(1,1:300),’b’)
hold on
plot(Y,’k’)
figure(2)
plot(x(1,1:300)-Y,’b’)
Etr=sqrt(sum((x(1,1:300)-Y).^2)/300)
Y=[];
for i=1:300
Y =[Y sim(net,xte(:,i))];
end
figure(3)
plot(yte,’k’)
hold on
plot(Y,’b’)
Ete=sqrt(sum((yte-Y).^2)/300)
figure(4)
plot(yte-Y,’b’)
- برنامه نوشته شده برای سیستم فازی :
clc
clear
T=30;
x=[1.2];
delta=1;
for i=2:T
x(i)=x(i-1)/1.1;
end
for i=T+1:round(600/delta)
x(i)=(1/1.1)*(x(i-1)+0.2*x(i-T)/(1+x(i-T)^10));
end
max_x=max(x)+0.2;
min_x=min(x)-0.2;
n=4;
sin=15;
stp=(max_x-min_x)/(sin-1);
y=min_x:0.01:max_x;
cent=min_x:stp:max_x;
% for i=1:sin
% k=trimf(y,[cent(i)-stp cent(i) cent(i)+stp]);
% end
so=15;
stp_o=(max_x-min_x)/(so-1);
cent_o=min_x:stp_o:max_x;
% for i=1:so
% k=trimf(y,[cent_o(i)-stp_o cent_o(i) cent_o(i)+stp_o]);
% end
for k=1:296
for t=1:4
for i=1:sin
mu_a(i)=trimf(x(k+t-1),[cent(i)-stp cent(i) cent(i)+stp]);
end
rule(k,t)=find(mu_a==max(mu_a));
rule_d(k,t)=max(mu_a);
end
for i=1:so
mu_b(i)=trimf(x(k+4),[cent_o(i)-stp_o cent_o(i) cent_o(i)+stp_o]);
end
B(k,1)=find(mu_b==max(mu_b));
B_d(k,1)=max(mu_b);
end
D=prod(rule_d’)’.*B_d;
for i=296:-1:1
for j=i-1:-1:1
if rule(i,:)==rule(j,:)
if D(j)<D(i)
D(j)=-inf;
else
D(i)=D(j);
B(i)=B(j);
D(j)=-inf;
end
end
end
end
for i=296:-1:1
if D(i)==-inf
D(i)=[];
rule(i,:)=[];
B(i)=[];
end
end
l_rule=length(rule);
hold on;
for u=1:596
suming_s=0;
suming_m=0;
pro=ones(1,l_rule);
y=[x(u) x(u+1) x(u+2) x(u+3)];
for k=1:l_rule
for t=1:4
pro(k)=pro(k)*trimf(y(t),[cent(rule(k,t))-stp cent(rule(k,t)) cent(rule(k,t))+stp]);
end
suming_s=suming_s+pro(k)*cent_o(B(k));
suming_m=suming_m+pro(k);
end
f(u+4)=suming_s/suming_m;
end
plot(x(1,1:300),’b’)
hold on
plot(f(1,1:300),’r’)
figure(2)
plot(x(1,1:300)-f(1,1:300),’b’)
Etr=sqrt(sum((x(1,1:300)-f(1:300)).^2)/300)
figure(3)
plot(x(1,301:600),’r’)
hold on
plot(f(1,301:600),’b’)
Ete=sqrt(sum((x(1,301:600)-f(1,301:600)).^2)/300)
figure(4)
plot(x(1,301:600)-f(1,301:600),’r’)
- برنامه نوشته شده برای شبکه PNN :
clc
clear
load(‘E:\shenasaey projeh\x’);load(‘E:\shenasaey projeh\xte’);load(‘E:\shenasaey projeh\yte’)
load(‘E:\shenasaey projeh\ytr’);load(‘E:\shenasaey projeh\xtr’)
c=[];
[sx,lx]=size(xtr);
y_col=[ytr;yte];
zte=[]; % khoroji laye 1
ztr=[];
xpd=cell(1,3);
ff=0;preE=10^10;
while 1
ff=ff+1
t=0;
for i=1:lx-1
for j=i+1:lx
t=t+1;
xpd{t}=Xpd([xtr(:,i) xtr(:,j)]);
end
end
for k=1:3
c(k,:)=inv(xpd{k}’*xpd{k})*xpd{k}’*ytr;
end
for kk=1:297
ztr=[ztr quad(xtr(kk,:),c)];
end
for kk=1:300
zte=[zte quad(xte(kk,:),c)];
end
z=[ztr’;zte’];
E_col=[];
for k=1:3
e=0;
for jj=1:597
e=e+(y_col(jj,1)-z(jj,k))^2;
end
u=e/597;
E_col=[E_col sqrt(u)];
end
xtr=ztr’;xte=zte’;
zz=z;
z=[];
if min(preE)<=min(E_col)
break
end
preE=E_col;
ztr1=ztr;zte1=zte;
ztr=[];zte=[];
[sx,lx]=size(xtr);
xpd=[];
end
Etr=[];
for k=1:3
e=0;
for jj=1:297
e=e+(y_col(jj,1)-zz(jj,k))^2;
end
u=e/297;
Etr=[Etr sqrt(u)]
end
Ete=[];
for k=1:3
e=0;
for jj=298:597
e=e+(y_col(jj,1)-zz(jj,k))^2;
end
u=e/300;
Ete=[Ete sqrt(u)]
end
y_col=[x(1:3)’; y_col];
figure(1)
plot(y_col(1:300,1))
hold on
ztr1=ztr1′;
zte1=zte1′;
ztr=[ztr1(:,1);zte1(:,1)];
ztr=[x(1:3)’;ztr];
plot(ztr(1:300,1),’r’)
s=(y_col-ztr);
figure(2)
plot(s)
figure(3)
plot(y_col(301:600,1))
hold on
plot(ztr(301:600,1),’r’)
s=(y_col(301:600,1)-ztr(301:600,1));
figure(4)
plot(s)
5- M-FILE مربوط به آموزش شبکه عصبی – ژنتیک GBSON :
clc
clear
load(‘C:\Documents and Settings\PC\Desktop\New Folder\Dtr’)
load(‘C:\Documents and Settings\PC\Desktop\New Folder\Dte’)
x=Dtr(:,1:3); % dadeye vorodi
xte=Dte(:,1:3);yte=Dte(:,4);
[sx,lx]=size(x);ytr=Dtr(:,4); % khoroji matlob
y_col=[ytr;yte];cs=[];c_f=[];P=20;l=128;
yyte=[]; % khoroji laye
Pc=.95;Pm=.1;q=6;
a1=cell(1,3);
c=cell(1,3);
c_laye=[];
xu=cell(1,3);
for laye=1:15
E=[];
ztr_col=[];ztr=[];
aa=[];a_new=[];
n=300;
for i=1:3
a1{i}=randint(P,l); %matrice valedin
end
for node=1:3
k=node;
a=a1{node};
for g=1:3500
E=[];
i=1;
while i<5
for ii=1:P
c_f(ii,i)=2.^(-1:-1:-29)*a(ii,32*(5-i)-28:(32*(5-i)))’;
cs(ii,i)=bi2de(a(ii,32*(5-i)-30:32*(5-i)-29),’left-msb’)+c_f(ii,i); %halgheye ijade sabetha
if a(ii,32*(5-i)-31)==1
cs(ii,i)=-cs(ii,i);
end
end
i=i+1;
end
for i=1:P %halgheye be dast avardane khoroji
xpd=Xpd(x,k);
for kk=1:300
ztr=[ztr;sum(xpd(kk,:).*cs(i,:))];
end
ztr_col(:,i)=ztr;
ztr=[];
end
syy=0;
for i=1:P %halgheye be dast avardane khata
for j=1:300
syy=syy+(ztr_col(j,i)-ytr(j,1))^2;
end
E=[E;sqrt((1/n)*(syy))];
syy=0;
end
if rem(g,50)==0
g
laye
E(1:3,:)
cs(1:3,:)
end
e=E;
fd=[];
ii=0;
while ii<3
ii=ii+1;
fd=find(e==min(e));
if length(fd)>1
for j=2:length(fd)
e(fd(j,1),1)=10^5*e(fd(j,1),1);
end
end
a_e(ii,:)=a(fd(1,1),:);
[sa,la]=size(a_e);
e(fd(1,1),:)=10^5*e(fd(1,1),:);
cr=[];
if sa>2
cr=[];
for k1=1:sa
for k2=k1+1:sa
if k1~=k2
k3=1;
cu=0;
while k3<128
if a_e(k1,k3)==a_e(k2,k3)
cu=cu+1;
end
k3=k3+32;
end
if cu==4
cr=[cr k2];
end
end
end
end
end
if cr~=0
if length(cr)==3
a_e(2:3,:)=[];
ii=ii-2;
end
if length(cr)==1
a_e(cr(1),:)=[];
ii=ii-1;
end
end
fd=[];
end
for i=1:P %halgheye fitnes
f(i,1)=1/(E(i,1));
end
sum_f=sum(f(1,:));
ss=0;
m=0;
for tt=1:P/2 %halgheye tolide farzandan
o=[];
while m<2 %halgheye entekhabe 2 valed
ff=[];
for i=1:q
rd=fix(P*rand)+1;
o=[o;a(rd,:)];
ff=[ff;f(rd,1)];
end
sum_ff=sum(ff(1,:));
r=sum_ff*rand;
for i=1:q
if ss<r
ss=ss+ff(i);
end
if ss>r
aa=[aa;o(i,:)];
ss=0;
r=sum_ff*rand;
[m,vv]=size(aa);
end
if m==2
ss=0;
break
end
end
end
a_old=aa;
ri=fix((l-2)*rand)+1;
rr=rand;
if rr<Pc %halgheye entekhabe cross over
for j=ri:l
a_old(1,j)=aa(2,j);
a_old(2,j)=aa(1,j);
end
ii=i+1;
else
ii=l;
end
for j=1:2 %halgheye mutation
for i=ii:l
zz=rand;
if zz<Pm
if a_old(j,i)==1
a_old(j,i)=0;
else
a_old(j,i)=1;
end
end
end
end
a_new=[a_new;a_old];
a_old=[];
aa=[];
m=0;
end %payane GA
a=a_new;
[tss,tse]=size(a_e);
for i=1:tss % halgheye jaygozinie behtarinhaye nasle ghabl ba nasle bad
if i<4
a(i,:)=a_e(i,:);
else
break
end
end
a_e=[];
a_new=[];
ztr=[];
end
E=[];
for i=1:P % halgheye mohasebeye khorojiha
xpd=Xpd(x,k);
for kk=1:300
ztr=[ztr;sum(xpd(kk,:).*cs(i,:))];
end
ztr_col(:,i)=ztr;
ztr=[];
end
syy=0;
for i=1:P % halgheye mohasebeye khataye khorojiha
for j=1:300
syy=syy+(ztr_col(j,i)-ytr(j,1))^2;
end
E=[E;sqrt((1/n)*(syy))];
syy=0;
end
fd=find(E==min(E));
ztr(:,1)=ztr_col(:,fd(1,1));
E=[];
xu{node}=ztr;
c{node}=cs(fd(1,1),:);
ztr=[];
ztr_col=[];
end
for im=1:3
syy=0;
xdh=xu{im};
for j=1:300
syy=syy+(xdh(j,1)-ytr(j,1))^2;
end
E=[E;sqrt((1/n)*(syy))];
if E<.002
break
end
syy=0;
end
for i=1:3
x(:,i)=xu{i};
c_laye(i,:)=c{i};
end
c_col{laye}=c_laye
end
M-FILE مربوط به تست شبکه عصبی – ژنتیک GBSON در متلب :
clc
clear
load(‘C:\Documents and Settings\PC\Desktop\New Folder\Dte’);
load(‘i:\arshad\Genetic\genetic project\Gbson\tornoment\c_colbitavan62tr8001’);
xte=Dte(:,1:3);yte=Dte(:,4);E=[];
zte=[];Ecol=[];
for ij=1:4
css=c_col{1,ij};
zte_col=[];
for i=1:3 %halgheye be dast avardane khoroji
xpd=Xpd(xte,i);
for kk=1:297
zte=[zte;sum(xpd(kk,:).*css(i,:))];
end
zte_col(:,i)=zte;
zte=[];
end
syy=0;
for i=1:3 %halgheye be dast avardane khata
for j=1:297
syy=syy+(zte_col(j,i)-yte(j,1))^2;
end
E=[E;sqrt((1/297)*(syy))];
syy=0;
end
xte=zte_col;
Ecol=[Ecol E];
E=[];
end
zte1=xte(:,3);
figure(1)
plot(yte)
hold on
plot(zte1,’r’)
s=(yte-zte1);
figure(2)
plot(s)
مراجع:
1.A Design of EA-based Self-Organizing Polynomial Neural Networks using
Evolutionary Algorithm for Nonlinear System Modeling
Dong-Won Kim and Gwi-Tae Park
2. Implementation of Artificial Intelligence in the Time Series Prediction Problem, L. EKONOMOU, S.SP. PAPPAS, September 22-24, 2006
3. Time Series PredictionUsingEvolving Polynomial Neural Networks, Amalia Foka, 1999
تهیه این آموزش متلب با زحمت زیادی صورت گرفته لطفا در فضای مجازی نشر ندهید

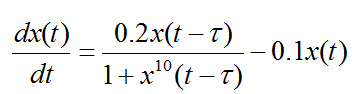
 هر چه تعداد نرون ها بیشتر شود تعمیم پذیری شبکه (جواب آن به داده های تست) بدتر می شود .
هر چه تعداد نرون ها بیشتر شود تعمیم پذیری شبکه (جواب آن به داده های تست) بدتر می شود .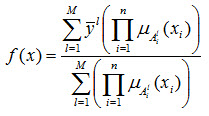
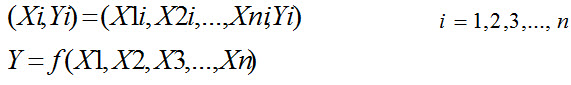
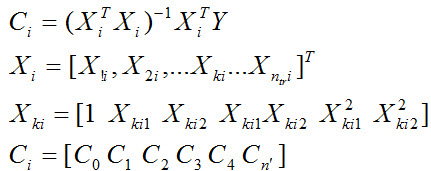






دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.