توضیحات
کنترل و پایدارسازی بازوی مکانیکی روبات با استفاده از تئوری معادلات ریکارتی وابسته به حالت
روش SDRE(State dependent ricatti equation) یک روش کنترلی وابسته به حالت می باشد. معادله ریکاتی وابسته به حالت یکی از ابزارهای قدرتمند برای طراحی کنترل کننده برای سیستم های غیرخطی می باشد. این کنترل کننده که می تواند یک کنترل کننده بهینه نیز تلقی شود بر اساس تبدیل معادلات غیرخطی به معادلات شبه خطی می باشد. هنوز هیچ کنترل کننده بهینه ای برای سیستم های غیرخطی به جز روش معادله ریکاتی وابسته به حالت SDRE ارائه نشده است. هدف از این روش کنترلی، یافتن ورودی کنترلی u است که با اعمال آن به سیستم تحت کنترل ضمن پایدار شدن سیستم و ارضا شدن قیود تعریف شده برای آن، تابع هزینه تعریف شده در معادله زیر مینیمم شود و ضمنا متغیرهای حالت سیستم با کمترین تلاش کنترلی به سمت صفر همگرا گردند
با تبدیل فرم معادله غیر خطی به فرم زیر ضرایب و ماتریس A و b در متلب تعریف میشوند.
برای اجرای برنامه ، SDRE_main اجرا میشود که در خط پنجم برنامه ،برنامه SDRE_Inputs فراخوانی میشود در SDRE_Inputs ثابتهای برنامه تعریف شده است.(ماتریس AوBوQوشرایط اولیه)
a1=0.0308;
a2=0.0106;
a3=0.0095;
a4=0.20907;
a5=0.0630;
g=9.8;
…
فقط قسمتی از کد متلب اینجا آورده شده است
Q=diag([1.2,0.005,1.5,0.005]);
R=diag(1);
H=zeros(4);
B='[0;(a2)/(a1*a2-a3^2*(cos(X(3))^2));0;(-a2-a3*cos(X(3)))/(a1*a2-a3^2*(cos(X(3))^2))]’;
در خط هفتم برنامه معادله دیفرانسیل غیرخطی در هر مرحله حل میشود. که معادله دیفرانسیل غیر خطی در هر مرحله به شکل زیر است.(sdre_ode45) برنامه زیر خط اول گین k را در هر مرحله طوری تععین میکند که تابع هزینه بالا مینیمم باشد سپس u را برابر –kx قرار داده و معادله دیفرانسیل dx=ax+bu را تشکیل داده و در برنامه sdre_main به حل این معادله میپردازد.
[~,~,K]=care(A1,B1,Q,R);%%%peyda kardane gaine K ke tabe hazine minimum bashad
u(:,I)=-K*X;…
یعنی در هر مرحله مقدار بهره فیدبک K آپدیت میشود تا با اعمال به سیستم غیر خطی حالت سیستم مشخص شود.
A1=eval(A);
B1=eval(B);
…
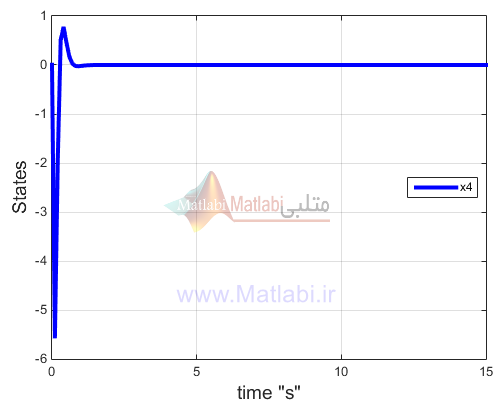
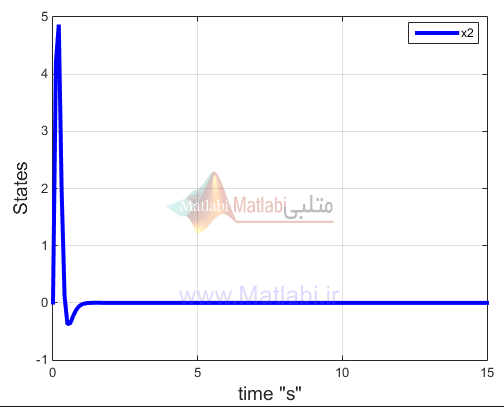
پس از آن برنامه به رسم حالتهای سیستم میپردازد. (sdre_plots)سیستم در کل 4 حالت دارد که هدف پایدار سازی این حالتهاست.با اجرای برنامه میبینیم که 4 حالت با گذشت زمان به سمت صفر میروند و پایدار هستند این 4 حالت همان تتا1 تتا2 و مشتقاتشان هستند.
نتیجه شبیه سازی کنترل کننده در سیستم روبات با شرایط اولیه x_initial=[-0.7,0.005,0.7,0.005]
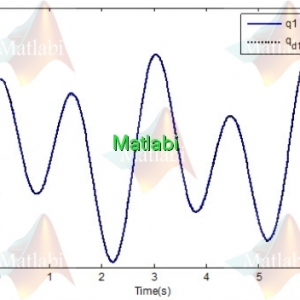
به شکل زیر است.) برای اجرا فایل main اجرا شود). شکل زیر متغیر حالت 1 یا همان x1=Ө1-pi/2 را نشان میدهد. همانطور که میبینیم با اعمال کنترل کننده سیستم پایدار شده است
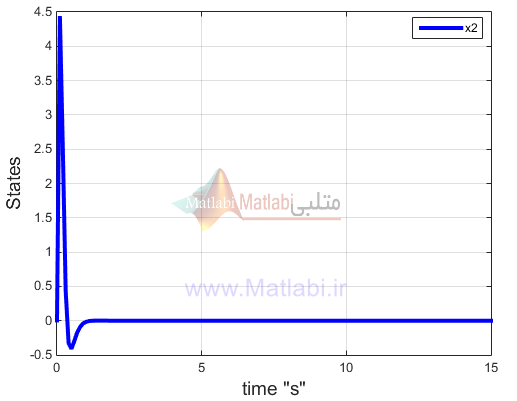
شکل زیر متغیر حالت دوم که همان مشتق تتا1 یا سرعت زاویه ای تتا1 است را نشان میدهد
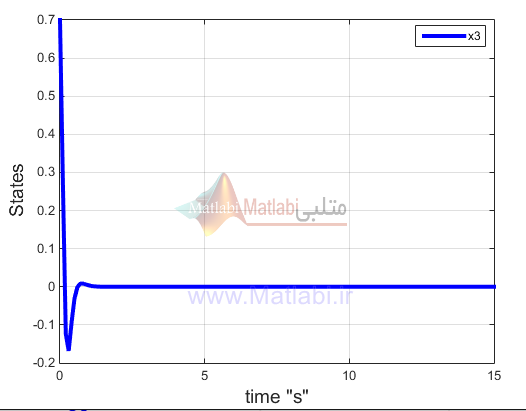
این شکل تتا2 را نشان میدهد که کنترل کننده این حالت از سیستم را پایدار کرده است
شکل زیر مشتق تتا2 را نشان میدهد
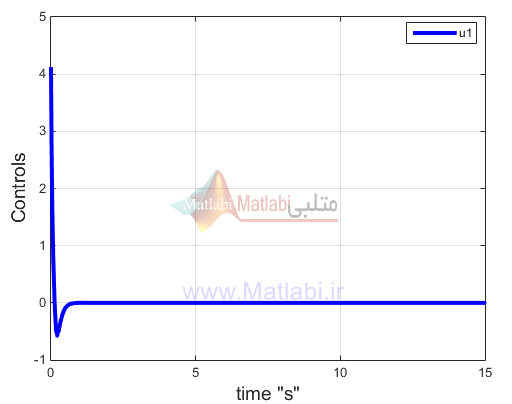
شکل زیر سیگنال کنترلی u اعمالی به سیستم را نشان میدهد که میبینیم سیگنالی یکنواخت است
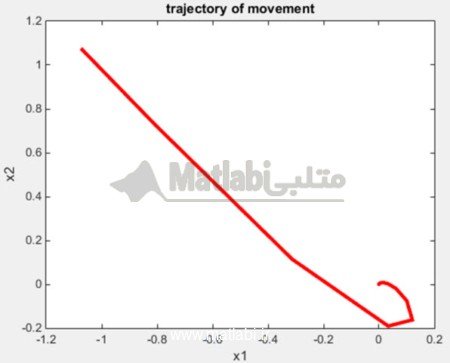
شکل زیر مسیر حرکت روبات را در صفحه نشان میدهد
حال شرایط اولیه را طبق خواسته مقاله عوض میکنیم میبینیم که باز هم سیستم پایدار است.
برای شرایط اولیه x_initial=[-1.7,0.005,1.7,0.005];پاسخها به شکل زیر است.
همانطور که مشاهده میکنیم پاسخ SDRE به شرایط اولیه بستگی دارد در کل تنظیم SDRE نسبت به تنظیم LQR همیشه هموارتر است و حاشیه پایداری مناسبی دارد همچنین چون از مدل غیرخطی استفاده میکند دارای دقت کنترل بالاتری میباشد
کلید واژه:پروژه متلب,شبیه سازی بامتلب
بازوی مکانیکی ربات, معادلات ریکاتی وابسته به حالت, تنظیم کننده مربعی خطی
شبیه سازی مقاله کنترل و پایدارسازی بازوی مکانیکی روبات با استفاده از تئوری معادلات ریکارتی وابسته به حالت
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.










دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.