توضیحات
Time-varying acceleration coefficients IPSO for solving dynamic economic dispatch with non-smooth cost function
در متن زیر روابط نیامده است ولی در گزارش وجود دارند.
مقدمه
برای حل مسائل پخش بار روش های بسیاری ارائه شده است که اکثر آنها بر اساس برنامه ریزی خطی روش لاگرانـژ و روشهای نیوتن- رافسون می باشد. یک مزیت مهم این روشـها سازگاری آنها با برنامه های توزیع اقتصـادی موجـود اسـت. علاوه بر این نیز روش های دیگری بر اساس برنامه ریزی خطـی ارائه شده است [3،2]. روش های بر اسـاس برنامـه ریـزی خطـی توابع غير خطی هزینه را خطی مـی کننـد و بـا حـل متـوالی مسئله اصلاح شده در هر تکرار جواب بهینه را پیدا می کنند.
محاسبه پخش بار يكي از اساسي ترين مسائل در صنعت برق است . در مسئله پخش بار پاسخ تكراري مجموعه بزرگي از معادلات خطي از قسمتهاي وقت گير شبيه سازي سيستم هاي قدرت ميباشد. عيب اصلي همه روشهاي پيشرفته مقدار بسيار زياد محاسبات مورد نياز مي باشد . اين امر به خاطرعمليات تجزيه ، تركيب و محاسبات ماتريس ژاكوبين مي باشد اجراي درست اين روشها در شبكه هايي با ابعاد وسيع نا كارا و منجر به حافظه و زمان محاسبات اضافي مي شود. بنابراين نياز ضروري به يك روش جديد تا بتواند نسبت به روشهاي موجود سريعتر حل گردد وجود دارد.
چنانكه ذکر شد مسأله پخش بار بهينه را ميتوان به صورت يك مسأله بهينه سازي غيرخطي با چند تابع هدف نشان داد. در بخش بزرگي از کارهاي تحقيقاتي که در اين زمينه انجام شده است يكي از سه هدف کاهش هزينه ها، بهبود امنيت سيستم و يا کاهش تأثيرات نامساعد زيست محيطي به تنهایي به عنوان تابع هدف مورد توجه قرار گرفته است و براي حل آنها از الگوريتم هاي برنامه ريزي غيرخطي متعددي که هر يك داراي محاسن و کاستي هايي باشند استفاده به عمل آمده است. در صورتي که بهبود عملكرد در يك بازه زماني مورد توجه باشد مسأله بهينه سازي وارد مرحله بسيار پيچيده اي مي گردد و در اين راستا مسائل گوناگون و عوامل متعددی بر رفتار سيستم مطرح مي گردد که در ادامه به اختصار و به طور اجمالي به چند مورد اشاره مي شود:
- برنامه ريزي ساعتي در مدار قرار گرفتن نيروگاه ها. بدين معني که در يك ساعت معين چه واحدهايي وارد مدار گرديده و يا ازآن خارج مي گرددند. اين مسأله به در مدار قرار دادن نيروگاه ها موسوم مي باشد.
- برنامه ريزي ساعتي توليد نيروگاه هاي آبي براساس محاسبات مربوط به سطح آب شيب مخازن آب و سدها جهت بهبود عملكرد سيستم. اين موضوع به هماهنگي نيروگاههاي آبي و حرارتي معروف مي باشد.
- برنامه ريزي ساعتي توليد واحدهاي حرارتي چند منظوره و پراکنده مثل نيروگاه هاي فتوولتائيك خورشيدي يا نيروگاه هاي بادي. اين مسأله به مسأله توليد واحدهاي پراکنده موسوم مي باشد.
- تعيين ميزان و ترتيب دورهاي واحدها، بدون نقض ظرفيت رزرو کافي و مناسب مورد نياز سيستم و در عين حال کمينه نمودن هزينه توليد. اين موضوع به برنامه ريزي تعميرات موسوم می باشد.
در مورد هر يك از گزينه های فوق، يك بازه زماني مناسب جهت بهينه سازي بايد انتخاب گردد. به عنوان مثال براي گزينه در مدار قرار دادن نيروگاه ها بازه زماني عملي و مناسب بين ٢٨ تا ۴٨ ساعت مي باشد در حالي که در گزينه هماهنگي واحدهاي آبي و حرارتي اين زمان از يك روز تا يك هفته، يك ماه و يا حتي يك سال متغير مي باشد. در برنامه ريزي تعميرات بازه زماني توأمأ بين يك تا سه سال انتخاب مي شود به طوري که بنا به ارتباطات قوي و وابستگي موارد مذکور به يکديگر نمي توان هريك از بخش هاي مورد اشاره را با توجه به بازه هاي زماني متفاوت به طور مجزا و مستقل از يكديگر مورد بررسي قرار داد. در جدول زیر بازه زماني عملي و مناسب هر يك از اين موارد و چگونگي ارتباط در سطوح مختلف بهينه سازي سيستم قدرت نشان داده شده است [4-7].
بازه زمانی ارتباطات و وابستگی در سطوح مختلف بهینه سازی سیستم قدرت
| زمان | فراِیند کنترلی | تابع بهینه شونده |
| ثانیه | کنترل خودکار تولید | بهینه سازی خطای کنترل ناحیه با درنظر گرفتن قیود دینامیکی |
| دقیقه | پخش بار اقتصادی | بهینه سازی لحظه ای بهره برداری با قیود معلوم |
| ساعت | اختصاص واحدهای آبی و حرارتی | بهینه سازی هزینه بهره برداری |
| هفته | هماهنگی تبادل ناحیه ها | بهینه سازی هزینه ها با در نظر گرفتن قیود قابلیت اطمینان |
| ماه | برنامه ریزی تعمیرات | بهینه سازی هزینه ها با در نظر گرفتن قیود قابلیت اطمینان |
| سال | طراحی تولید | بهینه سازی سرمایه گذاری و هزینه های ساخت |
اهمیت بررسی پخش بار اقتصادی و بهینه سازی آن
از آنجائي كه صنعت برق هر روز بيش از گذشته در عرصه رقابت تنگاتنگ گام بر می دارد اهميت و لزوم به کارگيري نرم افزارهاي پخش بار به منظور حدأکثر استفاده از سيستم انتقال و نيروگاه هاي توليد برق بيش از پيش نمايان و احساس مي گردد. نظر به امكان انتخاب توابع هدف گوناگون جهت بهينه سازي سيستم و اعمال قيود و محدوديت هاي متعدد و متفاوت بر روي اجزاي سيستم و شرايط بهره برداري از آن کاربردهاي گوناگون و متنوعي براي پخش بار موجود است که در زير به اختصار به ارائه عناوين و ويژگي ها، کاربردها و اهداف OPF و اهميت مطالعه و بررسي آن پرداخته مي شود [8].
- تعيين توان توليدي ژنراتورها و ديگر متغيرهاي قابل کنترل به منظور بهينه نمودن هزينه توليد و قيمت تمام شده برق توليدي با در نظر گرفتن محدوديت ها و قيود سيستم انتقال.
- کاهش تلفات.
- با در دست داشتن وضعيت موجود سيستم قدرت و يا برآورد بار کوتاه مدت آن مي توان با استفاده از پخش بار بهينه با لحاظ کردن محدوديت ها و قيود امنيت سيستم يك توزيع بار بازدارنده انجام داد.
- در وضعيت هاي اضطراري يعني در مواقعي که بعضي از اجزای سيستم قدرت دچار اضافه بار مي گردند و يا ولتاژ برخي از شينها از دامنه مجازشان تجاوز نموده اند پخش بار بهينه مي تواند با محاسبه و تعيين تنظيمات متغيرهاي قابل کنترل سيستم يك توزيع بار اصلاح کننده را ترتیب دهد.
- با اجراي پريوديك و متناوب پخش بار بهينه تنظيمات مناسب و بهينه متغيرهاي قابل کنترل سيستم شامل ولتاژ ژنراتورها، موقعيت ترانسفورماتورهاي تپ چنجر دار، دامنه و زاويه ترانسفورماتورهاي با تغيير دهنده فاز ، مقدار خازنهاي سوئيچ شونده و زاويه مطلوب جبران کننده های استاتيكي توان راکتيو تعيين مي گردد. اين ويژگي ها به بهينه سازي ولت- وار موسوم است.
- طراحي و برنامه ريزي خازن هاي سري؛ پخش بار بهينه قادر است که جابجايي و ميزان جبران سازي بهينه را براي خازن هاي سري در سيستم قدرت انجام دهد. به اين وسيله صرفه جویي هاي اقتصادي چشم گيري در به تعويق انداختن احداث خطوط انتقال جديد و افزايش ظرفيت انتقال سيستم موجود به عمل مي آيد.
- پخش بار بهينه به طور مستمر در مطالعات برنامه ريزي به منظور تعيين حدأکثر حد انتقال (شامل محدوديت هاي ناشي از پايداري ولتاژ) به کار مي رود. به اين وسيله ميتوان حدأکثر تواني را که با قابليت اطمينان مناسب از يك منطقه به منطقه ديگر منتقل مي شود را به دست آورد.
- در مطالعات اقتصادي سيستم قدرت، پخش بار بهينه در محاسبات و تعيين هزينه هاي افزايشي شين ها کاربرد فراوان دارد. به طوری که OPF در محاسبه هزينه انتقال توان يك شرکت برق از طريق شبكه واسط شرکت ديگر به مشترکين و يا شرکت ثالث نقش به سزايي را ايفا مي کند.
- پخش بار بهينه در محاسبات تمام شده حق اشتراك مشترکين و تعيين تعرفه ها از اهميت قابل توجهي برخوردار است.
- پخش بار بهينه به عنوان يك زيربرنامه در برنامه هاي پيچيده و بزرگي مانند به مدار آوردن نيروگاه ها، برنامه ريزي تعميرات، هماهنگي نيروگاه هاي آبي و حرارتي، کنترل اتوماتيك سيستم توليد و برنامه ريزي توليد کاربرد دارد و در واقع به عنوان يك ابزار اصلي در هر مرحله از تكرار، برنامه هاي مذکور فراخوانده مي شود و اجرا مي گردند.
- پخش بار بهينه با تابع هدف حداقل سازي آلودگي ناشي از احتراق سوخت هاي فسيلي، الگويي از ميزان توليد هر يك از واحدها را به گون هاي که کل آلودگي ناشي از احتراق سوخت هاي فسيلي کمينه باشد ارائه مي نمايد.
- پخش بار بهينه در ارائه شبكه هاي پايه و بررسي طرق توسعه شبكه هاي موجود مطابق با نياز سال هاي آينده کاربرد فراوان و نقش کليدي دارد.
- پخش بار بهينه در آشكارسازي نقاط ضعف شبكه ها مورد استفاده قرار مي گيرد.
OPF
مسأله پخش بار بهينه در سال ١٩۶٢ توسط آقاي کارپنتير در ابتدا به عنوان يك مسأله توزيع اقتصادي شبكه بيان شد [13]. پس از آن مسأله OPF به طور جدي مطالعه گرديد و به طور وسيعي در طراحي و عملکرد سيستم هاي قدرت به کار گرفته شد. تنوع کارهايي را که در OPF انجام شده است بيشتر به روش هاي بهينه سازي مورد استفاده در حل مسأله مربوط مي شود. در اين راستا در مرجع [14] مروري جامع و همه جانبه صورت گرفته است و تحقيقات و کارهاي انجام شده در زمينه OPF با توجه به روشهاي بهينه سازي استفاده شده جهت حل مسأله طبقه بندي و به صورت يك نمودار که نشان گر ارتباط بين روشها، متأثر بودن، همزماني با يكديگر، ميزان موفقيت، شهرت و دوام روش ها ارائه گرديده است. مهمترين گروه در جهت OPF گروهي است که در آن هزينه توليد (سوخت مصرفي) به عنوان تابع هدف انتخاب و حدأقل مي گردد. پخش بار بهينه به دنبال يافتن تنظيماتي براي استفاده بهينه از شبكه قدرت مي باشد که هدف آن دست آوردن پاسخ بهينه يك تابع هدف مانند هزينه سوخت در سيستم قدرت معين مي باشد که به وسيله تنظيم متغيرهاي کنترل سيستم هاي قدرت به طوري که يك سري از قيدهاي فيزيكي و عملكردي سيستم را برآورده سازد امکان پذير می باشد. متغيرهاي کنترل شامل: توان حقيقي ژنراتورها، ولتاژ باس های ژنراتور، ميزان تپ ترانسفورماتور و توليدات توان راکتيو منابع AVR مي باشد. متغيرهاي حالت نیز شامل: توان باس مرجع، ولتاژ باس هاي بار، توان خروجي ژنراتورها و توان هاي شارش شده در شبكه مي باشد. قيود مساوی مسأله شامل محدوديت روی معادلات پخش بار و قيود نامساوی شامل محدوديت هاي روی متغيرهاي کنترل و حالت سيستم می باشد. بنابراين مسأله پخش بار بهينه OPF مي تواند به عنوان يك مسأله بهينه سازي مقيد غيرخطي فرمول بندي گردد [15]. براي حل مسأله OPF ، روش هاي متعددي براي بهينه سازي به کار برده شده است که در این فصل به تعدادی از آنها اشاره می شود.
پخش بار اقتصادی (Economic Dispatching) در دنیای امروز مهمترین هدف توزیع انرژی در مراکز تولید است.در صنعت وقتی ژنراتور با بارهای مختلف به هم پیوسته است، ظرفیت تولید معمولا بسیار بزرگتر از بارهاست، از این رو تخصیص بارها در ژنراتور می تواند متنوع باشد، از آنجاییکه کاهش هزینه تولید برق مهم است ،پس تقسیم بار اقتصادی مورد نظر است.بیشترین هزینه تولید مربوط به هزینه سوخت می باشد. سایر هزینه ها شامل کار، تعمیرات و نگهداری اینها عوامل اقتصادی هستند. در نهایت متخصصین توزیع انرژی باید کنترل تولید نیروگاه ها را بر اساس کم ترین هزینه به دست گیرند. در محاسبات پخش بار اقتصادی به طور معمول از دو مسیر استفاده می شود:
مسیر اول، مدل کردن کل شبکه بر حسب تلفات توان و مسیر دوم مدل کردن شبکه بر حسب معادلات پخش بار می باشد.
شرط لازم برای تابع f (x ) = f (x1, x2 ,…, xn ) برای داشتن مقدار مینیمم با برقراری شرط زیر حاصل میشود [16-27]:
…
که با استفاده از اپراتور که گرادیان نامیده می شود، می توان عبارت H با مشتق دومF را چنین نمایش داد:
…
سپس نتایج در یک ماتریس متقارن که تابع عملکرد F نامیده می شود ذخیره می شود. فرض کنید:
…
که یک اکسترمم محلی است. لذا برای این که حداقل شود ، ماتریس H باید مقدار معین مثبتی باشد. این موضوع می تواند با پیدا کردن مقادیر ویژه ماتریس H چک شود ، همه آنها باید در مثبت باشد.
بهینه سازی پارامتر محدود (برابری محدودیتها)
در اینجا فرض می شود که F(x) در معرض محدودیت زیر حداقل گردد:
…
چنین مشکلاتی با استفاده از ضرایب لاگرانژ قابل حل است بنابراین :
…
شرایط لازم برای کمینه محدود نسبی L به شرح زیر است :
…
توجه داشته باشید که معادله آخر همان محدودیت های اصلی است.
بهینه سازی مقید پارامترها (محدودیتهای نامساوی)
مسایل عملی بهینه سازی دارای محدودیتهای تساوی و نا مساوی هستند. مساله مورد نظر کمینه سازی تابع هزینه f (x ) = f (x1, x2 ,…, xn ) است که محدودیتهای تساوی و نامساوی عبارتند از:
…
با تعمیم ضرایب لاگرانژ محدودیتهای نامساوی بوسیله معرفی بردار m تایی µ ازکمیت های تعیین نشده پوشش داده می شود. تابع هزینه بدون محدودیت بصورت زیر در می آید:
…
شرایط لازم بدست آمده برای نقاط کمینه محلی مقید عبارتند از:
…
توجه کنید که دومین معادله از معادلات اخیر همان محدودیتهای تساوی هستند.
عمده هزینه اجرای نیروگاه هزینه سوخت است.بقیه هزینهها میتواند به هزینه سوخت افزوده شود.معمولا هزینه سوخت با واحد دلار بر ساعت محاسبه میشود و یک تابع تولید توان بر حسب MW دارد.منحنی بهای سوخت معمولا به صورت سهمی در نظر گرفته میشود که از رابطه زیر نتیجه میشود:
…
منحنی “هزینه سوخت افزایشی” شیب منحنی “هزینه سوخت” است که توسط فرمول زیر تعریف میشود:
…
منحنی هزینه سوخت افزایشی نشان میدهد که چگونه افزایش هزینه سوخت بر افزایش هزینه تولید توان اثر میگذارد.واحد Ciدلار بر ساعت و دلار بر مگاوات ساعت است.
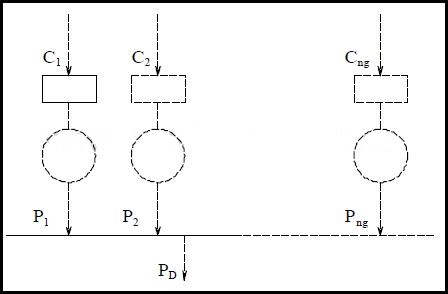
پخش بار اقتصادی با صرفنظر کردن از تلفات و محدودیت تولید ژنراتورها
راحت ترین حالت بررسی پخش بار قتصادی این است که تمامی ژنراتورها در یک شین باشند و یا تلفات خط برابر صفر باشد.فرض میکنیم که تعداد n ژنراتور را داریم که همگی به یک شین متصل شده اند و باری(بارهایی) را به اندازه PD تغذیه میکنند.
سعی ما بر این است که هزینه تولید را تا حد امکان کاهش دهیم.هزینه ما برابر خواهد بود با:
…
و برای بارها خواهیم داشت:
…
این حالت در شکل زیر نشان داده شده است:
شماتیکی از توان های تولیدی و توان بار کل [27]
دقت شود که تعداد ژنراتورهای قابل پخشبار ng برای تعداد n ژنراتور است. این بدین معنی است که n-ng ژنراتور برای پخش بار اقتصادی در نظر گرفته نمیشوند (این حالت در بارهای یک دست رخ میدهد، مثل ژنراتورهای هستهای،یا در حدهای بالا و پایین تولید ژنراتور). لذا از فرمولهای فوق بدست می آید:…
به منظور برآورده کردن شرایط لازم برای حداقل شدن تابع هدف داریم:…
اولین شرط نتیجه میدهد:…
بنابراین:…
پس شرط پخش بار بهینه برابرست با:…
به زبان سادهتر،با فرض اینکه هیچ محدودیتی در تولید برای ژنراتورها وجود ندارد و تلفات نیز صفر است،اقتصادیترین حالت عملیات وقتی است که همه نیروگاهها افزایش قیمت گاما را داشته باشند و جمع مقادیر تولید با بار مورد تقاضا برابر باشد.
از معادله فوق داریم:…
روابطی که بوسیله معادله فوق بدست میآید معادلات هماهنگ نامیده میشود.با استفاده از این معادله داریم:..
که از رابطه فوق به آسانی می توان گاما را محاسبه نمود. سپس با دانستن گاما میتوانیم Pi را با استفاده از فرمول 1-19 محاسبه کنیم. در مواردی که سیستم قدرت فاقد تلفات است (یعنی ژنراتورها در شینهای مشترک هستند) انجام پخش بار بهینه با استفاده از تحلیل بینشی کار آسانی است.اما در حالت کلی وقتی که تلفات قابل توجه است و ژنراتورها از لحاظ جغرافیایی از هم جدا هستند نمیتوان حاسبات را ه صورت عینی انجام داد.در این قبیل مسائل حل از روش تکرار به کار گرفته میشود.چنین راه حلی برای سیستمهای بدون تلفات در زیر آورده شده است (اگرچه حل این مسئله با تحلیل عینی آسان است اما حل آن به روش تکرار ما را در مسائلی که روش تکرار ضرورت است به ما تجربه میدهد).
پخش بار اقتصادی با چشم پوشی از تلفات و در نظر گرفتن محدودیتهای ژنراتورها
در دنیای واقعی ژنراتورها هم از لحاظ بیشینه و هم از لحاظ کمینه توان تولیدی معین و محدودی دارند. پس می توان نوشت:…
که به شرط اصلی اضافه می شوند.
شرایط کوهن تاکر تکمیل کننده شرایط لاگرانژ برای در بر گرفتن محدودیتهای نا مساوی به عنوان چند جمله اضافی هستند. شرایط لازم برای توزیع بهینه و بدون در نظر گرفتن تلفات به صورت زیر اند:…
حل عددی مشابه همان روش قبلی است ،یعنی برای یک λ تخمینی، توانها برای ژنراتورها بدست می آید . اگر این توان خارج از محدوده توان ژنراتور باشد ژنراتور در آن حد بالا یا پایین تثبیت می گردد. در این شرایط دیگر این ژنراتورها به تولید بهینه کمکی نخواهند کرد و تنها نیروگاه هایی که در محدوده مجاز قرار دارند باید در هزینه افزایشی مساوی شرکت کنند.
روش پخش بار با در نظر گرفتن تلفات شبکه
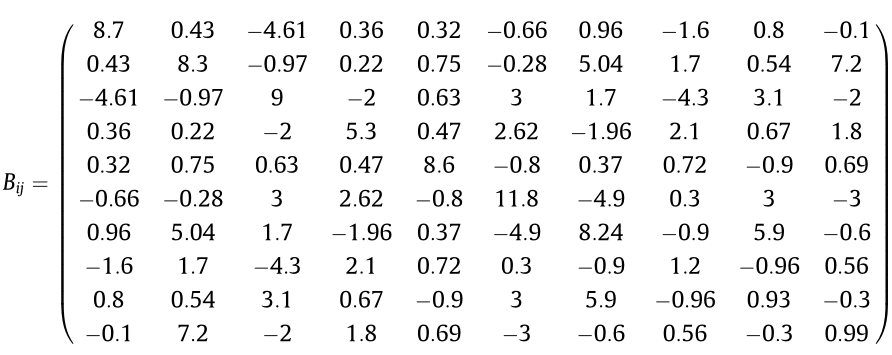
هنگامی که فواصل انتقال بسیار کم و چگالی بار خیلی زیاد باشد ، می توان از تلفات انتقال چشم پوشی کرده و توزیع بهینه تولید را با بهره برداری از همه نیروگاه ها بدست آورد. هر چند ، در یک شبکه بهم پیوسته بزرگ با فواصل طویل تلفات انتقال قابل توجه بوده و باید لحاظ گردد. حال از فرمول کرون به صورت زیر استفاده می شود [28]:
…
ضرایب Bij ضرایب تلفات نامیده می شوند .این ضرایب با درصد خطای خوبی ثابت فرض می شوند (با در نظر گرفتن فرضهای اولیه صحیح). مساله توزیع اقتصادی کمینه سازی هزینه تولید Ci است و داریم:…
با توجه به اینکه توان تولیدی برابر توان مصرفی بعلاوه توان تلف شده است داریم:…
و محدودیتهای نا مساوی عبارتند از:…
که دران Pi ها محدودیت حداقل و حاکثر نیروگاه i می باشد. با استفاده از ضرایب لاگرانژ و افزودن جملات اضافی برای در بر گرفتن محدودیتهای تساوی خواهیم داشت:…
باید در مورد محدودیتهای دانست که وقتی باشد بوده وهنگامی که بوده برابر با صفر خواهد بود. به عبارت دیگر اگر قید از مقدار خودش تجاوز نکرده باشد، متغییر µ مرتبط با آن صفر بوده وعبارت مربوط در معادله بالا وجود نخواهد داشت.این قید زمانی مطرح است که تخلفی رخ داده باشد.
برای بدست آوردن حداقل مقدار داریم:…
دو معادله آخر نشان می دهند که توان نباید از مقدار محدوده تجاوز کند و در داخل محدوده داریم:…
و تابع کوهن تاکر مانند تابع لاگرانژ خواهد شد و از آنجایی که Ct = C1 + C2+ L+ Cng خواهیم داشت:…
قسمت تلفات انتقالی افزایشی نامیده می شود. شرط دوم از رابطه 2-3 محاسبه می شود. این معادله همان محدودیتهای تساوی است که باید رعایت گردد. شکل کلاسیک فرمول بالا به صورت زیر است:…
که در آن Li ضریب جریمه نیروگاه i نامیده می شود. پس اثر تلفات انتقال معرف یک ضریب جریمه است که مقدار آن به موقعیت مکانی نیروگاه بستگی دارد. از معادله بالا واضح است که هزینه کمینه زمانی بدست میآید که حاصل ضرب هزینه افزایشی هر نیروگاه و ضریب جریمه آن برای تمام نیروگاه ها مساوی باشد.
هزینه تولید افزایشی از معادله تلفات بدست میآید وتلفات افزایشی انتقال با استفاده از فرمول تلفات به قرار زیر است:…
همین طور هزینه تولید افزایشی به صورت زیر است:…
با استفاده از این رابطه می توان نوشت:…
با گسترش معادله بالا برای تمامی نیروگاه ها به صورت ماتریسی، تمامی مجهولات به دست می آیند و مساله پخش بار اقتصادی حل می گردد. یعنی برای تعیین توزیع بهینه با مقدار تخمین اولیه (1) ، باید معادلات خطی بالا همزمان حل گردند.
پخش بار اقتصادی با استفاده از روش فرا ابتکاری مبتنی بر جمعیت
توزيع بار اقتصادي ديناميک توان خروجي همه نيروگاه ها را طي تمامي بازه هاي زماني توزيع بار جهت کمينه کردن کل هزينه سوخت، مشخص مي کند. به گونه اي که قيدهاي مشخصي برآورده شوند. مسئله توزيع بار اقتصادي بر اساس کمينه کردن هزينه سوخت و بدون توجه به شرط آلودگي طراحي شده است. برخي از گازهاي آلاينده ناشي از سوخت فسيلي واحدهاي حرارتي نظير SO2 ،NO ،CO و … به صورت مستقيم و غيرمستقيم بر سلامتي انسان تأثيرگذار هستند. تـوزيع بار اقتصادي هزينه-آلودگي ديناميک[1] (DEED) مي تواند بهعنوان روشي جهت در نظر گرفتن شـرط آلودگي در مسئله DED[2] به کار برده شود. DEED يک مسئله بهينه سازي چندهدفه است که هزينه سوخت و آلودگي را به طور همزمان تحت شرط نرخ-شيب و ساير قيدها کمينه مي کند [29]. در پخش بار دینامیکی به منظور اجتناب از کم شدن طول عمر تجهیزات، بهره برداران نیروگاه سعی می کنند تا گرادیان حرارت و فشار درون دیگ های بخار و توربین ها را در یک محدوده ی ایمن نگاه دارند. این محدودیت مکانیکی به صورت محدودیت نرخ افزایش یا کاهش توان الکتریکی خروجی منعکس می شود. این حد، محدوده ی نرخ شیب نامیده می شود که مسئله ی پخش بار اقتصادی دینامیکی را از پخش بار اقتصادی استاتیک متمایز می کند.
فرمول بندی مسئله توزیع بار اقتصادی-آلودگی دینامیکی (DEED)
(DEED) يک مسئله بهينه سازي جهت مشخص نمودن برنامه توليد هريک از نيروگاه ها به گونه اي است که همزمان هزينه سوخت کل و آلودگي در کل دوره توزيع کمينه شده و مجموعه اي از قيود مساوي و نامساوي برآورده شوند. توابع هدف و قيدهاي بسیاری در فرمولبندي مسئله DEED در نظر گرفته مي شوند؛ نظیر تابع سوخت.
تابع هزینه سوخت
هزينه سوخت واحدهاي توليدي معمولاً توسط يک تابع درجه دوم تقريب زده مي شود. در اينگونه نيروگاه ها، توربين ها معمولاً داراي چندين دريچه بخار هستند که جهت کنترل توان خروجي هر واحد استفاده مي شوند. فرآيند باز شدن دريچه بخار در توربين هايي که چندين دريچه بخار دارند، نمودار سرعت گرمايي توربين را موج دار مي کند و همچنين، موجب منفصل و غير محدب شدن تابع هزينه مي شود. براي مدل کردن دقيق اثرات دريچه بخار، يک تابع سينوسي به تابع هزينه اضافه مي شود. بنابراين، تابع هزينه سوخت کل در تمام دوره توزيع در نظر گرفتن اثر نقطه-دريچه در رابطه زیر نشان داده شده است….
در رابطه فوق:ضرايب منحني تابع سوخت مربوط به واحد iام؛ و نشانگر اثر نقطه-دريچه هستند؛ T تعداد ساعتهايي که سيستم مورد مطالعه قرار مي گيرد؛ Ng تعداد واحدهاي توليدي موجود در مدار؛ توان توليدي خروجي واحد iام در طول دوره tام (ساعت tام)؛ حداقل توان توليدي مجاز واحد iام می باشند.
تابع آلودگی
تابع آلودگي مي تواند توسط دو روش مختلف فرمول بندي شود. در روش اول، اهداف آلودگي NO و SO به صورت دو تابع درجه دو مجزا در نظر گرفته می شود. در روش دوم که در اين مدل استفاده شده است، تابع آلودگي نيروگاه هاي سوخت فسيلي به صورت ترکيب اهداف آلودگي NO و SO است که به صورت مجموع يک تابع درجه دو و يک تابع نمايي مدل شده است .
روش پیشنهادی و برآورده سازی قیود
پيش از بيان نحوه پاسخ گويي به مدل پيشنهادي توسط الگوريتم هاي فرا ابتکاري، لازم است به اين نکته اشاره شود که تفاوت اصلي مسئله توزيع بار اقتصادي استاتيک و ديناميک، تنها به دليل وجود قيد نرخ شيب است. پاسخ به مسئله توزيع بار اقتصادي ديناميک در طول يک دوره (۲۴ ساعت) با تقسيم کل دوره به تعدادي بازه هاي زماني کوچکتر (بازه هاي يک ساعتي) و سپس حل مسئله توزيع بار اقتصادي استاتيک براي هـر بـازه تحت قيد نرخ-شيب بين بازه هاي مختلف حل مي شود. نظر به توضيحات فوق و با توجه به طبيعت احتمالاتي الگوريتم هاي فرا ابتکاري، براي به دست آوردن نتايج با دقت بيشتر، مدل ارائه شده با ده بار حل مسئله توزيع بار استاتيکي در هر ساعت پاسخ داده شده است. جهت حل مدل پيشنهادي و برآورده نمودن قيود واقعي سيستم روند کلي زير ارائه مي شود.
- مرحله ۱ .تعريف داده هاي اوليه واحدها، منحني بار روزانه ، ماتريس الاستيسيته قيمت؛ تنظيم مقدار اوليه نرخ تشويق در مقدار صفر، تنظيم تعداد ساعات مورد مطالعه براي يک شبانه روز ، تعيين تعداد تکرارهاي الگوريتم بهينه سازي.
- مرحله ۲ .افزايش مقدار نرخ تشويق به اندازه گام تغييرات آن توسط. ISO
- مرحله ۳ .تنظيم شماره ساعت بر روي صفر
- مرحله 4. t=t+1
- مرحله ۵ .تعيين مقدار تقاضاي بار در هر ساعت
- مرحله ۶ .تنظيم تعداد حل مسئله توزيع بار اقتصادي روي مقدار صفر
- مرحله 7 .تعيين جمعيت اوليه الگوريتم بهينه سازي
- مرحله ۹ .اجراي حلقه اصلي الگوريتم بهينه سازي انتخاب شده.
این روش بر روی یک سيستم ۱۰ ژنراتوري پیاده سازی شده است و توزیع اقتصادی بار ارزیابی گردیده است. مدل پيشنهادي DEED داراي يک سري مزايا شامل کاهش هزينه سوخت و آلودگي، تعيين مقدار تشويق بهينه و بهبود شاخص هاي منحني بار شامل ضريب بار و شاخص هاي درصد اختلاف پيک و دره، نسبت جبران پيک و نسبت جبران اختلاف پيک و دره است. برنامه پاسخگويي بار اضطراري بر اساس ماتريس الاستيسته قيمت توسعه داده شده که در واقع يکي از روش هاي قدرتمند مدل سازي بار در برنامه هاي پاسخ گويي بار است. اگر چنانچه مقدار تشويق بهينه به درستي مشخص نشود، ممکن است باعث تحميل هزينه هاي اضافي در سمت توليد شود [30].
پخش بار اقتصادی با استفاده از روش برنامه ریزی مربعی
پخش بار اقتصادي ديناميكي با برنامه ريزي خروجي آنلاين ژنراتورها با تقاضاهاي بار پـيش بينـي شـده در بـازه زمـاني مشخص به منظور بيشترين عملكرد اقتصادي سيستم قدرت الكتريكي سر و كار دارد. اين مدل روش تركيبي الگوريتم بهينه سازي كاوش باكتري با برنامه ريزي مربعي متوالي براي حل مسأله پخش بار اقتصادي واحدهاي توليدي با در نظـر گـرفتن اثـرات نقطـه شير را پيشنهاد مي كند. اين روش تركيبي، بهينه سازي كاوش باكتري را به عنوان جستجوي سطح پايـه كـه مـي توانـد جهـت يـابي مناسبي به ناحيه بهينه داشته باشد و برنامه ريزي مربعي متوالي را به عنوان روال جستجوي محلي كه براي تنظـيم دقيـق آن ناحيـه براي رسيدن به حل نهايي به كار مي رود، به كار مي گيرد.
در دهه اخير الگوريتم PSO که بر مبناي روشهاي تحقيق تصادفي است براي بهينهسازي کلي[3]، بر اساس مدلهايي از دستگاههای اجتماعي ساده توسط ابرهارت[4] و سايرين ارائه شد و مشخص شد که در حل مسائل غیرخطی، مانند مسئله بهينهسازي توزيع توان راکتيو بسيار کارآمد است. خصوصيات اين الگوريتم بهصورت زير است]36-45[.
- اين الگوريتم بر اساس تحقيقاتي در مورد اجتماعات مختلف نظير اجتماع پرندگان بناشده است.
- اين الگوريتم بر اساس يک مفهوم بسيار ساده بناشده است. بنابراين زمان لازم براي محاسبات بسيار کم ميباشد و حافظه زيادي نياز ندارد.
- اين الگوريتم براي مسائل بهینهسازی غيرخطي و پيوسته ابداعشده است. بااینحال میتوان براي مسائلي که متغيرهاي گسسته دارند نيز از اين الگوريتم استفاده نمود.
مورد سوم از خصوصيات اين الگوريتم براي مسئله توزيع بهينه توان راکتيو بسيار حائز اهميت است زيرا روش مؤثری که بتواند متغيرهاي گسسته را نيز در نظر بگيرد وجود ندارد.
بر اساس مطالعاتي که بر روي اجتماعات گوناگون مانند اجتماع پرندگان انجامشده است اين فرضيه وجود دارد که هرگونه اطلاعاتي در بين جمعيت آن تبادل ميشود. علاوه بر اين، بر اساس مشاهدات اجتماعات انساني، رفتارهاي هر فرد متأثر از رفتارهاي افراد ديگر اجتماع ميباشد. اين فرضيات پايه مفاهيم الگوريتم PSO میباشد. الگوریتم PSO بر اساس اجتماع پرندگان در فضاي دوبعدی توسعهیافته است. موقعيت هر فرد از اين اجتماع بر اساس يک نقطه در فضاي دوبعدي XY میباشد. بردار سرعت در راستاي محور X با و سرعت فرد در راستاي محور Y با نمايش داده ميشود. اصلاح موقعيت فرد با استفاده از موقعيت و بردار حرکت آن انجام ميشود.
مسائل بهينه سازي به طور گسترده اي در زمينه هاي مختلف علوم و فنآوري به کار گرفته مي شوند. گاهي اوقات چنين مسائلي مي تواند با توجه به ماهيت واقعي و عملي تابع هدف يا قيود مدل بسيار پيچيده باشند. روش هاي بهينه سازي سنتی دربرگيرنده تکنيک هاي مبتني بر مشق گيري هستند. چنين روش هايي نيرومند بوده و کارايي آنها در حل انواع مختلف مسائل بهينه سازي به اثبات رسيده است. با اين وجود چنين روش هايي مي توانند با مشکلاتي ازقبيل گرفتار شدن در حدأقل محلي، افزايش پيچيدگي محاسباتي و قابل استفاده نبودن در دسته هاي معيني از توابع هدف، مواجه می- شوند. اين امر نياز براي توسعه دسته جديدي از روش هاي حل که مي تواند بر اين نقايص فائق آيد منجر مي شود. روش هاي بهينه سازي ابتکاري ، ابزارهاي در حال رشد سريعي هستند که مي توانند بر بيشتر محدوديت هايي که در روش هاي مبتني بر مشتق گيري يافت مي شود چيره شوند. برای درک کلی از مفهوم و ايده روش فوق با يک مثال کار را شروع می کنيم. فرض کنيد شما و گروهي از دوستانتان به دنبال گنج مي گرديد. هر يك از اعضاي گروه يك فلزياب و يك بيسيم دارند که مي تواند مكان و وضعيت کار خود را به همسايگان نزديك خود اطلاع بدهد. بنابراين شما مي دانيد که آيا همسايگانتان از شما به گنج نزديكترند يا نه؟ پس اگر همسايه اي به گنج نزديكتر بود شما مي توانيد به طرف او حرکت کنيد. با چنين کاري شانس شما براي رسيدن به گنج بيشتر مي شود و همچنين گنج زودتر از زماني که شما تنها باشيد پيدا مي شود.
اين يك مثال ساده از رفتار جمعي است که افراد براي رسيدن به يك هدف نهايي همكاري مي کنند. اين روش مؤثرتر از زماني است که افراد جداگانه عمل کنند. اجتماع را مي توان به صورت مجموعه اي سازمان يافته از موجوداتي تعريف کرد که با يكديگر همكاري مي کنند. در کاربردهاي محاسباتي هوش جمعی از موجوداتي مانند مورچه ها، زنبورها، موريانه ها، دسته هاي ماهيان و دسته پرندگان الگو برداري مي شود. در اين نوع اجتماعات هر يك از موجودات ساختار نسبتاً ساده اي دارند ولي رفتار جمعي آنها بي نهايت پيچيده است. براي مثال در کلوني مورچه ها هر يك از مورچه ها يك کار ساده مخصوصی را انجام مي دهند ولي به طور جمعي عمل و رفتار مورچه ها مانند ساختن بهينه لانه، محافظت ازملكه و نوزادان، تميز کردن لانه و… بسيار پيچيده می باشد. رفتار کلي يك ذره به صورت غيرخطي از آميزش رفتارهاي تك تك اجتماع بدست مي آيد، به عبارتي يك رابطه اي بسيار پيچيده بين رفتار جمعي و رفتار فردي يك اجتماع وجود دارد. رفتار جمعي فقط وابسته به رفتار فردي افراد اجتماع نيست بلكه به چگونگي تعامل ميان افراد نيز وابسته است. تعامل بين افراد، تجربه افراد درباره محيط را افزايش مي دهد و موجب پيشرفت اجتماع مي شود. ساختار اجتماعي بين افراد مجموعه کانالهاي ارتباطي ايجاد مي کند که طي آن افراد مي توانند به تبادل تجربه هاي شخصي بپردازند، مدل سازي محاسباتي اجتماعی کاربردهاي موفق و بسياري را در پي داشته است.
بهينه سازی اجتماع ذرات يکی از شاخه های هوش جمعی مي باشد که حوزه وسيعی از دانش هوش مصنوعی را شامل می شود. هوش جمعي در واقع بر پايه شبيه سازي رفتار جمعي گروهي از حشرات مانند، مورچه ها و موريانه ها، همين طور گروه حيواني، مانند پرندگان و ماهي ها شکل گرفته است. از شاخه هاي هوش جمعي، علاوه برPSO ، مي توان به روش اجتماع مورچگان اشاره کرد که درآن از تقليد رفتار جمعي از مورچگان در يافتن غذا براي مسائل مسيريابي بهينه استفاده مي شود. در ابتدا الگوريتم PSO به منظور کشف الگوهاي حاکم بر پرواز همزمان پرندگان و تغيير ناگهاني مسير آنها و تغيير شكل بهينه دسته به کار گرفته شد [34].
فرآيند جستجو بر اساس مفاهيم گفتهشده را میتوان به اين صورت شرح داد که يک دسته از افراد يک اجتماع، به دنبال بهينه کردن يک تابع هدف خاص ميباشند. هر فرد از اين اجتماع بهترين جواب تاريخچه خود و موقعيت کنوني خود را ميداند. علاوه بر اين هر فرد از بهترين جوابي که در تاريخچه جمعيت موجود است مطلع ميباشد. بردار حرکت اصلاحشده براي هر فرد را میتوان از رابطه زير به دست آورد]35 [:
…
که در رابطه بالا:
: بردار حرکت فرد iام در تکرار kام (تکرار جاري)
: بردار حرکت اصلاحشده براي فرد iام
rand : يک عدد تصادفي بين 0 و 1
: موقعيت جاري فرد iام در تکرار kام
: بهترين جواب فرد iام در تکرارهاي مختلف
: بهترين جواب در ميان تمامي افراد جامعه
: ضريب وزني براي بردار سرعت فرد iام
: ضريب وزني براي هر مولفه
با استفاده از معادلات بالا يک بردار حرکت که بهطور مشخص به pbest و gbest نزديک ميشود را ميتوان محاسبه نمود. موقعيت جاري هر فرد را ميتوان با استفاده از رابطه زير اصلاح نمود:…
شکل (3-1) مفهوم اصلاح نقاط جستجو را نمايش میدهد. متغيرهاي گسسته را ميتوان در روابط (3-1) و (3-2) باکمی اصلاحات اعمال نمود. اعداد گسسته را ميتوان براي بيان موقعيت و بردار سرعت فرد به کاربرد.
در فرآيند بالا حداکثر سرعت هر فرد بهوسیله مقدار حداکثر محدود ميشود .درواقع اين پارامتر دقت جستجوي فضا بين نقطه جاري و نقطه هدف را مشخص ميکند . اين محدوديت جستجوي محلي فضاي مسئله را بهبود ميبخشد. درصورتیکه اين پارامتر بسيار بزرگ انتخاب شود ممکن است افراد از روي
جوابهاي خوبي رد شوند، از طرفي اگر اين پارامتر بیشازاندازه کوچک انتخاب شود فرآيند جستجو به فضاهاي کوچکي محدود خواهد شد. در بسياري از مسائل بين 10 تا 20 از فضاي جستجوي هر متغير انتخاب ميشود.
علاوه بر الگوريتم هاي بهينه سازي سنتّي مبتني بر گراديان، بسياري از روش هاي ابتکاري ديگر نيز وجود دارند که با PSO به رقابت مي پردازند؛ از قبيل الگوريتم ژنتيک، برنامه ريزي هاي تکاملي، و اخيراً بهينه سازي الگوريتم مورچگان. در حالت کلي همان طور که بيشتر اين روش ها براي حل مسائل مختلف بهينه سازي به کار می رود، روش فوق نيز قادر به حل مسائل مختلف بهينه سازي می باشد. با اين وجود، بعضي از اين روش هاي رقيب، داراي کاستي ها و نقاط ضعفي از قبيل موارد زير هستند [36]:
- تنظيم پارامترهاي بيشتري نياز دارند
- به زمان محاسباتي زيادي نياز دارند
- توسعه و اصلاح الگوريتم هاي فوق براي منطبق کردن آنها با انواع مختلف مسائل بهينه سازي به مهارت برنامه نويسي زيادي مورد نياز است
- بعضي از اين روش ها نيازمند تبديل به حوزه باينري به جاي کار کردن با مقادير واقعي مستقيم متغيرها هستند
از سوي ديگر، برخي مزاياي روش هاي فوق الذکر در مقايسه با PSO به قرار زير است:
- نسخه هاي تجاري اين الگوريتم ها، مانند (Matlab ) براي الگوريتم ژنتيک و ( Excel solver premium ) براي برنامه ريزي هاي تکاملي در دسترس مي باشد
- مجموعه گسترده اي از کتاب ها و نوشته هاي تحقيقاتي، با استفاده از روش هاي رقيب به ويژه الگوريتم ژنتيک و برنامه نويسي تکاملي، صورت گرفته است
الگوریتم پیشنهادی
می دانیم اکه الگوریتم PSO بر پایه روابط 3-1 تا 3-7 استوار است. حال به منظور بهبود عملکرد الگوریتم PSO، یک ضریب جدید به رابطه 3-1 افزوده می گردد. لذا الگوریتم PSO قدیم به الگوریتم IPSO یعنی Iteration PSO تغییر نام پیدا می کند. لذا ضرایب سرعت به فرم رابطه 3-14 در می آیند:
که بهترین پاسخی است که توسط هر ذره در تکرارها حاصل می گردد. نیز ضریب وزنی متناسب با آن است. همچنین نیز یک عدد تصادفی در بازه 0 تا 1 می باشد. عملکرد این برنامه (و هر برنامه دیگری) تنها وابسته به تنظیم صحیح این ضرایب می باشد. در الگوریتم PSO سنتی، معمولا ضرایب روی 2 تنظیم می شدند. یکی از نقطه ضعف این تنظیم، ثابت بودن ضرایب است. یعنی اگر ضریب c2 از 2 بیشتر شود، اکثر مواقع پاسخ ها در اکسترمم محلی به دام می افتند. در الگوریتم ارائه شده پیشنهادی، ضرایب پویا می باشند و با روابط زیر محاسبه می گردند.
این موضوع باعث می شود تا ذره ها در ابتدا مجبور شوند تمامی فضای مساله را برای یافتن پاسخ جست و جو کنند. پس از گذشت کمی از حرکت ذره ها، به روز کردن ضرایب آنها را مجور می کند تا با سرعت بیشتری به بهینه سراسری همگرا شوند [39].
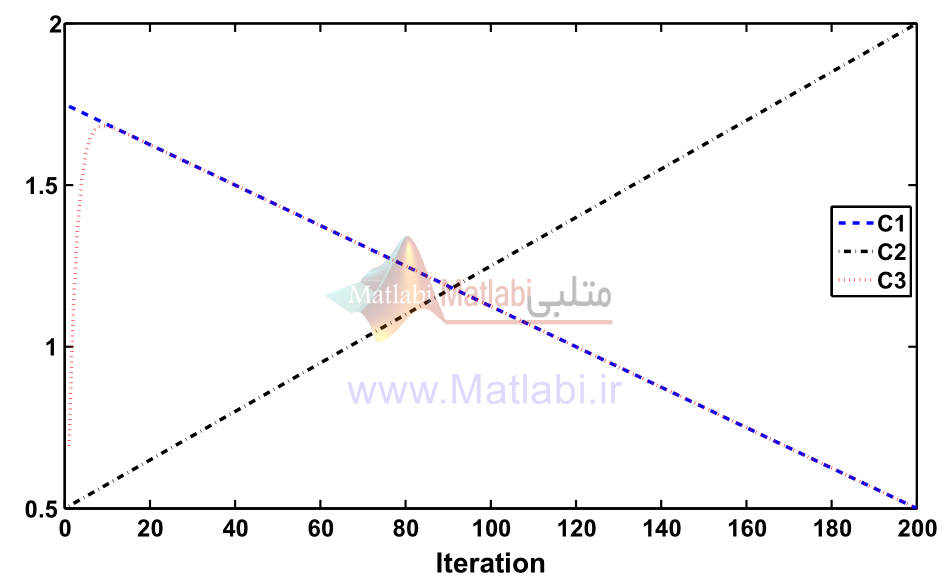
در شروع برنامه (تکرارهای ابتدایی)، ذره ها بسیار از نقطه بهیه فاصله دارند. لذا افزود یک جمله جدید به سرعت حرکت آنها، همگرایی ذره ها را بهبود می بخشد. لذا ضریب c3 را این چنین محاسبه می کنیم:
…
که در روابط فوق، نشان دهنده شماره تکرار و همان تکرار ماکزیمم می باشند.
با تنظیم ضرایب فوق به صورت : ، اگر تکرار ماکزیمم را 200 در نظر بگیریم، توزیع ضرایب بر حسب شماره تکرار را می توان در شکل 3-3 مشاهده نمود.
…
محاسبه تابع هدف با رابطه 2-40
به روز کردن سرعت و موقعیت با روابط 3-14 تا 3-17
Iter=1 , t=t+1
بله
خیر
Iter>Iter(max)
Iter=iter+1
خیر
بله
نمایش خروجی
t>t(max)
به روز کردن موقعیت ذرات
خیر
بله
Iter>Iter(max)
بله
خیر
پایان
ارضای قیود؟
مقدار دهی اولیه و iter=1
تولید جمعیت اولیه
شروع
توزیع ضرایب بر حسب شماره تکرار
فلوچارت الگوریتم PSO نیز مشابه شکل 3-2 است اما فقط رابطه به روز رسانی سرعت و موقعیت آن متفاوت است و شامل ضریب c3 نیست. در نهایت تابع هدف که با فرمول 3-18 ارائه می شود، همان هزینه های بهره برداری را نشان خواهد داد. ضرایب و پارامترها به تفصیل در فصل دوم معرفی شده اند. پس مساله اصلی در این کار کمینه کردن هزینه تولید توان با در نظر گرفتن اثر شیر بخار است.
تحلیل نتایج
در فصل سوم، الگوریتم PSO و IPSO به تفصیل شرح داده شدند. لذا در این فصل فورا به پیاده سازی الگوریتم در دو سیستم 5 شینه و 10 شینه می پردازیم. در ادامه منظور از واژه POZ ، منطقه ممنوعه بهره برداری می باشد که در فصول قبل مفهوم آن را روشن ساخته ایم. اکنون به سه مطالعه موردی، الگوریتم پیشنهادی را اعتبار سنجی می نماییم.
مطالعه موردی اول (بهره برداری بدون تاثیر POZ)
در این قسمت یک سیستم 5 واحدی را با استفاده از الگوریتم پیشنهادی مورد آزمایش قرار می دهیم. ضرایب و مشخصات این سیستم به شرح زیر می باشد.
| POZ | Pmax | Pmin | fi | ei | ci | bi | ai | واحد |
| [60 55] ، [30 25] | 75 | 10 | 042/0 | 100 | 25 | 2 | 008/0 | 1 |
| [90 80] ، [50 45] | 125 | 20 | 04/0 | 140 | 60 | 8/1 | 003/0 | 2 |
| [140 125] ، [70 60] | 175 | 30 | 038/0 | 160 | 100 | 2/1 | 0012/0 | 3 |
| [180 160] ، [110 95] | 250 | 40 | 037/0 | 180 | 120 | 2 | 001/0 | 4 |
| [200 175] ، [100 85] | 300 | 50 | 035/0 | 200 | 40 | 8/1 | 0015/0 | 5 |
بارهای ساعتی نیز برای سیستم مورد نظر در جدول زیر آورده شده است.
بار روزانه سیستم بر حسب مگاوات در 24 ساعت [6]
| میزان بار | ساعت |
| 410 | 1 |
| 435 | 2 |
| 475 | 3 |
| 530 | 4 |
| 558 | 5 |
| 608 | 6 |
| 626 | 7 |
| 654 | 8 |
| 690 | 9 |
| 704 | 10 |
| 720 | 11 |
| 740 | 12 |
| میزان بار | ساعت |
| 704 | 13 |
| 690 | 14 |
| 654 | 15 |
| 580 | 16 |
| 558 | 17 |
| 608 | 18 |
| 654 | 19 |
| 704 | 20 |
| 680 | 21 |
| 605 | 22 |
| 527 | 23 |
| 463 | 24 |
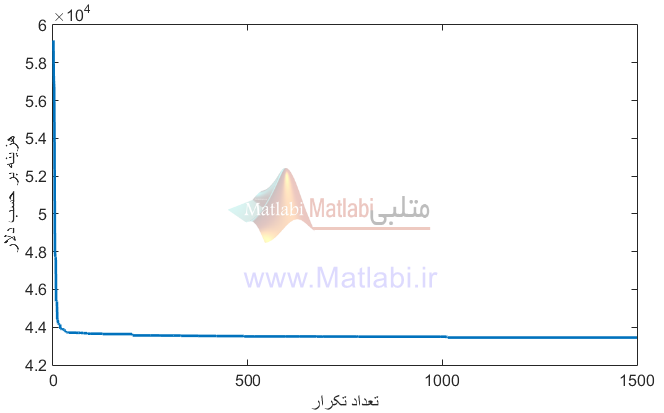
در این مطالعه موردی، تاثیر شیر بخار، تلفات خط انتقال، قیود نرخ ماکزیمم و مینیمم تولید ژنراتور ها و حد بالا و پایین توان تولیدی آنها مد نظر قرار گرفته است. اما [5]POZ را مورد بررسی قرار نداده ایم. تاثیر POZ در مطالعه موردی دوم در نظر گرفته شده است. میزان تکرار ماکزیمم در این حالت برابر با 1500 می باشد.
بسیاری از مراجع تا کنون مساله DED را با روشهای مختلف حل نموده اند. به عنوان نمونه جدول زیر، همین مساله را در سیستم 5 واحدی با استفاده از روشهای مختلفی که تاکنون آن را حل نموده اند، با هم مقایسه می کند.
منحنی بار روزانه در سیستم 5 واحدی
مقایسه روشهای موجود در حل مساله DED سیستم 5 شینه
| مدت زمان اجرای شبیه سازی برحسب دقیقه | هزینه برحسب دلار | روش |
| 86/5 | 47356 | SA [26] |
| – | 44678 | APSO [14] |
| 4 | 44384 | AIS [12] |
| 32/3 | 48625 | GA [6] |
| 55/3 | 44253 | PSO [6] |
| 29/3 | 44045 | ABC [6] |
| 024/0 | 49216 | MLS [7] |
| 53/4 | 46530 | IPS [10] |
روشهای فوق به ترتیب عبارتند از: الگوریتم ذوب شبیه سازی شده (SA) ، الگوریتم اردحام ذرات تطبیقی (APSO)، سیستم ایمنی مصنوعی (AIS)، الگوریتم ژنتیک (GA)، الگوریتم اذدحام ذرات (PSO)، الگوریتم کلونی زنبور عسل مصنوعی (ABC)، سری مک لورن (MLS)، الگوریتم جسجتوی الگوی بهبود یافته (IPS) می باشند.
حال سیستم مورد نظر تحت الگوریتم پیشنهادی اجرا می شود. شکل زیر، همگرایی هزینه بهره برداری را بر حسب تعداد تکرارها بیان می کند.
همگرایی هزینه بهره برداری بر حسب تعداد تکرار در حالت اول
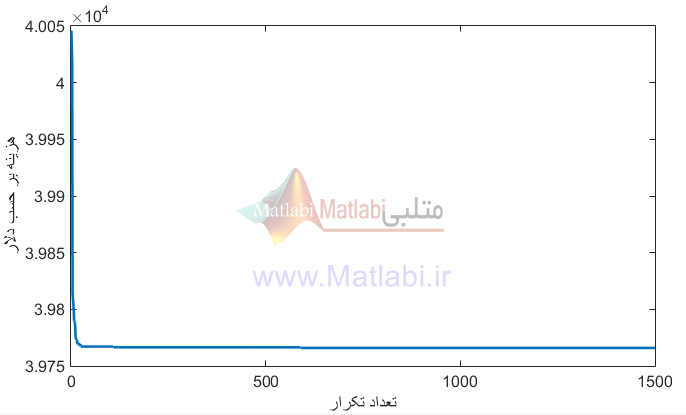
مطالعه موردی دوم (بهره برداری با تاثیر POZ)
در این قسمت تاثیر POZ را بر بهره برداری از سیستم 5 واحدی لحاظ می کنیم. تمامی مشخصات سیستم مانند حالت قبل است. شکل زیر نمودار همگرایی هزینه بهره برداری را بر حسب تعداد تکرارها بیان می کند.
همگرایی هزینه بهره برداری بر حسب تعداد تکرار در حالت دوم
در این مرحله یک سیستم 10 واحدی را با الگوریتم پیشنهادی در حل مساله DED مورد بررسی قرار می دهیم. در ابتدا مشخصات سیستم 10 واحدی در جدول 4-6 ذکر می گردد [6].
 |
مشخصات سیستم 10 واحدی مورد نظر
| Pmax | Pmin | fi | ei | ci | bi | ai | واحد |
| 470 | 150 | 041/0 | 450 | 958 | 6/21 | 00043/0 | 1 |
| 460 | 135 | 036/0 | 600 | 1313 | 05/21 | 00063/0 | 2 |
| 340 | 73 | 028/0 | 320 | 604 | 81/20 | 00039/0 | 3 |
| 300 | 60 | 052/0 | 260 | 471 | 9/23 | 0007/0 | 4 |
| 243 | 73 | 063/0 | 280 | 480 | 62/21 | 00079/0 | 5 |
| 160 | 57 | 048/0 | 310 | 601 | 87/17 | 00056/0 | 6 |
| 130 | 20 | 086/0 | 300 | 502 | 51/16 | 00211/0 | 7 |
| 120 | 47 | 082/0 | 340 | 639 | 23/23 | 00480/0 | 8 |
| 80 | 20 | 098/ | 270 | 455 | 58/19 | 10908/0 | 9 |
| 55 | 55 | 094/0 | 380 | 692 | 54/22 | 00951/0 | 10 |
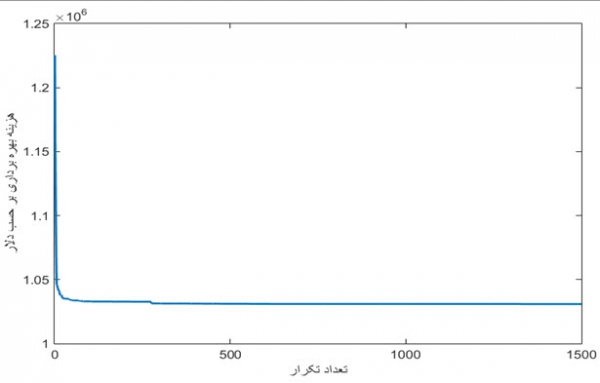
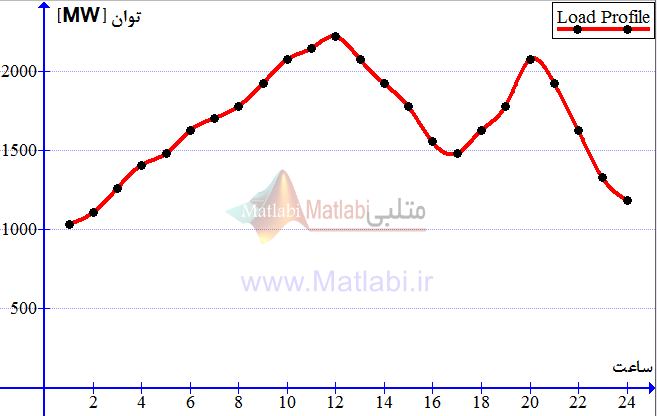
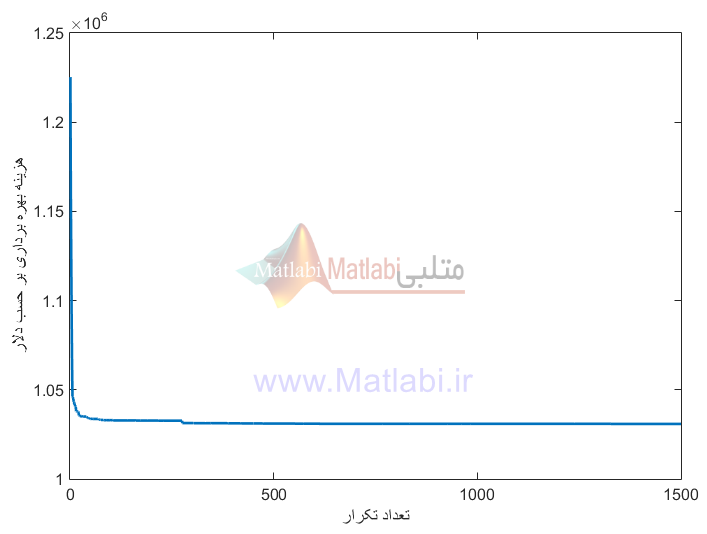
میزان بار درخواستی مشتریان نیز در جدول 4-7 به نمایش در آمده است. شکل 4-3 همگرایی تابع هدف را پس از چند تکرار محدود نشان می دهد. همانگونه که مشاهده می کنید، هزینه بهره برداری برابر با 1030900 دلار به دست آمده است. این در حالی است که اگر با سایر روش ها مقایسه گردد، بهترین نتیجه را دارا خواهد بود. صحت این موضوع در جدول 4-8 آورده شده است.
منحنی بار روزانه برای سیستم 10 واحدی
بار روزانه سیستم بر حسب مگاوات در 24 ساعت [6]
| میزان بار | ساعت |
| 1036 | 1 |
| 1110 | 2 |
| 1258 | 3 |
| 1406 | 4 |
| 1480 | 5 |
| 1628 | 6 |
| 1702 | 7 |
| 1776 | 8 |
| 1924 | 9 |
| 2072 | 10 |
| 2146 | 11 |
| 2220 | 12 |
| میزان بار | ساعت |
| 2072 | 13 |
| 1924 | 14 |
| 1776 | 15 |
| 1554 | 16 |
| 1480 | 17 |
| 1628 | 18 |
| 1776 | 19 |
| 2072 | 20 |
| 1924 | 21 |
| 1628 | 22 |
| 1332 | 23 |
| 1184 | 24 |
همگرایی تابع هزینه در مطالعه موردی سوم
مقایسه روشهای موجود در حل مساله DED سیستم 10 شینه
| مدت زمان اجرای شبیه سازی برحسب دقیقه | هزینه برحسب دلار | روش |
| 47 | 1054685 | EP [28] |
| 27 | 1052668 | EP-SQP [28] |
| 24 | 1050054 | MHEP-SQP [28] |
| 4/3 | 1052251 | GA [6] |
| 4 | 1048410 | PSO [6] |
| 4/3 | 1043381 | ABC [6] |
| 23 | 1045715 | AIS [12] |
روشهای ارائه شده در جدول به ترتیب برنامه ریزی تکاملی (EP)، برنامه ریزی تکاملی درجه دوم متوالی (EP-SQP)، برنامه ریزی تکاملی اصلاح شده درجه دوم متوالی (MHEP-SQP) می باشند. سایر روشها پیشتر معرفی شده اند.
پس بنابراین می توان نتیجه گرفت که الگوریتم پیشنهادی هم از لحاظ زمان و هزینه و هم از لحاظ دقت، بسیار قوی تر از سایر روشهای موجود ظاهر می شود. زیرا هم تابع هدف بهبود یافته است و هم مدت زمان حل به کمترین حد خود می رسد. این موضوع کاهش تولید واحدهای تولیدی در قبال افزایش راندمان را در پیش خواهد داشت.
- Dynamic economic emission dispatch ↑
- Dynamic economic dispatch ↑
- global ↑
- Eberhart ↑
- prohibited operating zones ↑
کلید واژه :
Dynamic economic dispatch, Time varying acceleration coefficients, iteration particle swarm optimization, Non-convex optimization
شبیه سازی مقاله Time-varying acceleration coefficients IPSO for solving dynamic economic dispatch with non-smooth cost function
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.



دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.