توضیحات
System identification and control of robot manipulator based on fuzzy adaptive differential evolution algorithm
شناسایی و کنترل ربات با استفاده از الگوریتم تکاملی فازی تطبیقی
سیستمهای فازی
منطق فازی یا Fuzzy Logic برای اولین بار در سال 1960 توسط دکتر لطفی زاده ، استاد علوم کامپیوتری دانشگاه برکلی کالیفرنیا (Berkeley)، ابداع شد.
مقاله کلاسیک پرفسور لطفی زاده درباره مجموعه فازی که در سال 1965 به چاپ رسید، سرآغاز جهتی نوین در علوم و مهندسی سیستم و کامپیوتر بود.
پس از آن پرفسور لطفی زاده به پژوهشهای خود در زمینه مجموعه فازی ادامه داد تا آنکه در سال 1973 طی یک مقاله کلاسیک دیگر تحت عنوان “شرحی بر دیدی نو در تجزیه و تحلیل سیستمهای پیچیده و فرایندهای تصمیم گیری” مفهوم استفاده از متغیرهای زبانی را در سیستم های حافظه و کنترل مطرح کرد.
این مقاله اساس تکنولوژی کنترل بر مبنای منطق فازی است که در اینده اثرات عمیق در طراحی سیستم های کنترل هوشیار خواهد داشت.
گرچه منطق فازی کاربردی خیلی وسیع تر از منطق متداول دارد ولی پرفسور لطفی زاده معتقد است که منطق فازی اکسیر و نوشدارو نیست.
وی میگوید “کارهای زیادی هست که انسان میتواند به آسانی انجام دهد در حالی که کامپیوترها و سیستمهای منطقی قادرت فازی یک فرا مجموعه از منطق بولی است که بر مفهوم درستی نسبی، دلالت می کند.
منطق کلاسیک هر چیزی را بر اساس یک سیستم دوتائی نشان می دهد ( درست یا غلط، 0 یا 1، سیاه یا سفید) ولی منطق فازی درستی هر چیزی را با یک عدد که مقدار آن بین صفر و یک است نشان می دهد. مثلاً اگر رنگ سیاه را عدد صفر و رنگ سفید را عدد 1 نشان دهیم، آن گاه رنگ خاکستری عددی نزدیک به صفر خواهد بود. در سال 1965، دکتر لطفیزاده نظریه سیستمهای فازی را معرفی کرد.
در فضایی که دانشمندان علوم مهندسی به دنبال روشهای ریاضی برای شکست دادن مسایل دشوارتر بودند، نظریه فازی به گونهای دیگر از مدلسازی، اقدام کرد.
منطق فازی معتقد است که ابهام در ماهیت علم است.
انجام پروژه های متلب با سایت متلبی
بر خلاف دیگران که معتقدند که باید تقریبها را دقیقتر کرد تا بهرهوری افزایش یابد، لطفیزاده معتقد است که باید به دنبال ساختن مدلهایی بود که ابهام را به عنوان بخشی از سیستم مدل کند. در منطق ارسطویی، یک دستهبندی درست و نادرست وجود دارد. تمام گزارهها درست یا نادرست هستند.
بنابراین جمله «هوا سرد است»، در مدل ارسطویی اساساً یک گزاره نمیباشد، چرا که مقدار سرد بودن برای افراد مختلف متفاوت است و این جمله اساساً همیشه درست یا همیشه نادرست نیست.
در منطق فازی، جملاتی هستند که مقداری درست و مقداری نادرست هستند. برای مثال، جمله “هوا سرد است” یک گزاره منطقی فازی میباشد که درستی آن گاهی کم و گاهی زیاد است. گاهی همیشه درست و گاهی همیشه نادرست و گاهی تا حدودی درست است.
منطق فازی میتواند پایهریز بنیانی برای فنآوری جدیدی باشد که چیست؟
نمونهای از کاربردهای منطق فازی
در اوائل دهه 1980 این زمینه از نقطه نظر تئوریک پیشرفت کندی داشت.در این مدت راه حل ها و مفاهیم جدید اندکی معرفی گردید چرا که هنوز افرادکمی داشتند روی ان کار می کردند.در واقع کاربردهای کنترل فازی بود که هنوز تئوری فازی را سر پا نگاه داشته بود.
مهندسان زاپنی(با حساسیتی که نسبی به فن اوری های جدید دارند)به سرعت دریافتند که کنترل کننده های فازی بسهولت قابل طراحی بوده و در مورد بسیاری مسائل می توان از انها استفاده کرد.
بدلیل اینکه کنترل فازی به یک مدل ریاضی نیاز ندارد انرا می توان در مورد با وجودی که تئوری فازی جایگاه واقعی خود را پیدا نکرد با این حال هنوز محققینی بودند که روشهای جدید فازی نظیر الگوریتم های فازی تصمیم گیری های فازی و… مطرح گردید.
اگر بگوییم پذیرفته شدن تئوری فازی بعنوان یک زمینه مستقل بواسطه کارهای بر جسته پروفسور لطفی زاده بوده سخن به گزاف نگفته ایم.بسیاری از مفاهیم بنیادی تئوری فازی بوسیله زاده در اواخر دهه 60 و اوائل دهه 70 مطرح گردید.
پس از معرفی مجموعه ای فازی در سال 1965 او مفاهیم الگوریتم های فازی در سال 1968 تصمیم گیری فازی در سال 1970 و ترتیب فازی را در سال 1971 مطرح نمود.در سال 1973او مقاله دیگری را منتشر کرد به نام :(طرح یک راه حل جدید برای تجزیه تحلیل سیستم های پیچیده و فرایندهای تصمیم گیری).
این مقاله اساس کنترل فازی را بنا کرد.او در این مفهوم متغییر های زبانی و استفاده از قواعد اگر انگاه را برای فرموله کردن دانش بشری معرفی نمود.
رخداد بزرگ در دهه 1970 تولد کنترل کننده های فازی برای سیستم های واقعی بود.
در سال 1975 ممدانی و اسیلیان چهارچوب اولیه ای را برای کنترل کننده فازی مشخص کردند و کنترل کننده فازی را به یک موتور بخار اعمال نمودند.
نتایج در مقاله ای تحت عنوان(ازمایشی در سنتز زبانی با استفاده از یک کنترل کننده فازی)منتشر گردید.انها دریافتند که ساخت کنترل کننده فازی بسیار موضوع جدی در دستور کار خود قرار دادند.
در فوریه1992 اولین کنفرانس بین المللی IEEEدر زمینه سیستمهای فازی در سان دیگو برگزار گردید.این یک اقدام سمبلیک در مورد پذیرفتن سیستم های فازی بوسیله بزرگترین سازمان مهندسی یعنی IEEEبود.در سال 1993 بخش سیستم های فازی IEEEگشایش یافت.
از نقطه نظر تئوری سیستم های فازی و کنترل در اواخر دهه 80 و اوائل دهه 90 رشد چشمگیری پیدا کرد و پیشرفتهایی در زمینه برخی مشکلات اساسی سیستمهای فازی صورت گرفت. بعنوان مثال تکنیک های شبکه عصبی برای تعیین و تنظیم توابع تعلق استفاده شدند.
با وجودی که تصویر سیستم های فازی شفاف تر شده با این حال کارهای زیادی هنوز باید انجام شود و بسیاری از راه حل ها و روش ها در ابتدای راه قرار دارد.
ما اعتقاد داریم که تنها سرمایه گذاری مراکز تحقیقاتی معتبر بر روی افراد مستعد و خلایق می تواند باعث پیشرفتهای عمده در زمینه تئوری فازی شود.
چرا سیستم فازی؟
واژه(فازی) در فرهنگ لغت اکسفورد بصورت (مبهم گنگ نادقیق کیج مغشوش درهم و نامشخص)تعریف شده است.
سیستم های فازی سیستم هایی هستند با تعریف دقیق و کنترل فازی نیز نوع خاصی از کنترل غیر خطی میباشد که ان هم تعریف می گردد.
این مطلب مشابه کنترل وسیستم های خطی می باشد که واژه(خطی) یک صفت فنی بوده که حالت و وضعیت سیستم و کنترل را مشخص می کند. چنین چیزی درمورد واژه(فازی) وجود دارد.
مشکلات سیستمهای فازی
موفقیت سیستم های فازی در زاپن تعجب محققان را در امریکا و اروپا برانگیخت.
عده ای هنوز به ان خرده می گرفتند ولی عده ای دیگراز عقیده خود دست بر داشته و بعنوان گرچه سیستم های فازی پدید های غیر قطعی و نا مشخص را توصیف می کنند با این حال خود تئوری فازی یک تئوری دقیق می باشد.
در این متن دو نوع موجیه برای تئوری سیستم های فازی وجود دارد:
_دنیای واقعی ما بسیار پیچیده تر از ان است که بتوان یک توصیف و تعریف دقیق برای ان بدست اورد بنابراین باید یک توصیف تقریبی یا همان فازی که قابل قبول تجزیه و تحلیل باشد برای یک مدل معرفی شود.
_با حرکت ما بسوی عصر اطلاعات دانش و معرفت بشری بسیار اهمیت پیدا می کند. بنابراین ما به فرضیه ای نیاز داریم که بتوان دانش بشری را به شکل سیستماتیک فرموله کرده و انرا به همراه سایر مدلهای ریاضی در سیستم های مهندسی قرار دهد.
توجیه اول گرچه درست است با این حال طبیعت واحدی را برای تئوری سیستم های فازی شخص نمی کند. در حقیقت تمامی نظریه های علوم مهندسی دنیای واقعی را به شکلی تقریبی توصیف می کنند.
بعنوان مثال در عالم واقع تمامی سیستم های خطی می باشد.یک تئوری مهندسی خوب از یکسو باید بتواند مشخصه های اصلی و کلیدی دنیای واقعی را توصیف کرده و از سویی دیگر قابل تجزیه تحلیل ریاضی باشد.بنابراین از این جنبه تئوری فازی تفاوتی با سایر تئوری های علوم مهندسی ندارند.
توجیه دوم مشخصه واحدی از سیستم های فازی را توصیف کرده و وجودی تئوری سیستم های فازی را به عنوان یک شاخصه مستقل در علوم مهندسی توجیه می کند.بعنوان یک قاعده کلی یک تئوری قاعده کلی یک تئوری مهندسی خوب باید قادر باشد از تمامی اطلاعات موجود به نحو موثری استفاده کند.
در سیستم های عملی اطلاعات مهم از دو منبع سر چشمه می گیرند.یکی از منابع افراد خبره می باشند که دانش و اگاهیشان را در مورد سیستم با زبان طبیعی تعریف می کنند.منبع دیگر اندازه گیری ها و مدل های ریاضی هستند که از قواعد فیزیکی مشتق شده اند.
بنابراین یک مسئله مهم ترکیب این دو نوع اطلاعات در طراحی سیستم ها است.
برای انجام این ترکیب سئوال کلیدی این است که چگونه می توان دانش بشری را به یک فرمول ریاضی تبدیل کرد. اساسا انچه که یک سیستم فازی انجام می دهد همین تبدیل است.برای اینکه بدانیم این تبدیل چگونه صورت می گیرد ابتدا باید بدانیم سیستم های فازی چگونه سیستم هایی هستند.
سیستم های فازی چگونه سیستم هایی هستند؟
سیستم های فازی سیستم ها مبتنی بردانش یا قواعد میباشد .قلب یک سیستم فازی یک پایگاه دانش بوده که از قواعد اگر-آنگاه فازی تشکیل شده است. یک قاعده اگر-آنگاه فازی یک عبارت اگر –آنگاه بوده که بعضی کلمات آن بوسیله توابع تعلق پیوسته مشخص شده اند.
بعنوان مثال عبارت فازی زیر را در نظر بگیرید: اگر سرعت اتومبیل بالاست انگاه نیروی کمتری به پدال گاز وارد کنید.
بطور کلی دو راه حل برای طراحی چنین کنترل کننده ای وجود دارد یک راه حل استفاده از کنترل کننده های متعارف نظیر PID بوده وراه حل دوم شبیه سازی رفتار رانندگان است بدین معنی که قواعدی که راننده در حین حرکت استفاده می کند را به کنترل کننده خودکار تبدیل نماییم.
ما راه حل دوم را در نظر میگیریم. در صحبتهای عامیانه راننده ها در شرایط طبیعی از سه قاعده زیر در حین رانندگی استفاده می کنند:
2-اگر سرعت پایین است آنگاه نیروی بیشتری به پدال گاز وارد کنید.
3-اگر سرعت متوسط است آنگاه نیروی متعادلی به پدال گاز وارد کنید
4.اگر سرعت بالاست آنگاه نیروی کمتری به پدال گاز وارد کنید .با این حال ما می توانیم یک سیستم فازی را بر اساس این قواعد بسازیم.از آنجا که سیستم فازی بعنوان کنترل کننده استفاده شده ان را کنترل کننده فازی می نامند. بطور خلاصه نقطه شروع ساخت یک سیستم فازی بدست اوردن مجموعه ای از قواعد اگر – انگاه فازی از دانش افراد خبره یا دانش حوزه مورد برسی می باشد.
مرحله بعدی ترکیب این قواعد در یک سیستم واحد است. معمولااز سه نوع سیستم فازی صحبت به میان می اید :
1)سیستم های فازی خالص
2)سیستم های فازی تاکاگی –سوگنو و کانگ TSK) )
3)سیستم های با فازی ساز و غیر فازی ساز
بطور خلاصه این سه نوع سیستم را شرح می دهیم ساختار اصلی یک سیستم فازی خالص در شکل 3 نشان داده شده است .پایگاه قواعد فازیمجموعه ای از قواعد اگر-آنگاه فازی را نشان می دهد.
موتور استنتاج فازی این قواعد را به یک نگاشت از مجموعه های فازی در فضای ورودی به مجموعه های فازی در فضای خروجی بر اساس اصول منطق فازی ترکیب می کند.
مشکل اصلی در رابطه با سیستم های فازی خالص این است که ورودی ها و خروجی های ان مجموعه های فازی می باشند (وازهایی در زبان طبیعی ).
برای حل این مشکل تاکاگی سوگنو و کانگ نوع دیگری سیستم های فازی معرفی کرده اند که ورودی ها و خروجی های ان متغییر هایی با مقادیر واقعی هستند. سیستم TSKبجای استفادهاز قواعدی به شکل 1 از قواعدی بدین صورت استفاده می کند :…
-اگر سرعت اتومبیل (X) بالاست انگاه نیروی وارد بر پدال گاز برابر است با Y=CX
که وازه(بالا) همان معنی 1 را داده و C یک عدد ثابت می با شد.
مقایسه نشان می دهد که بخش انگاه قاعده فازی از یک عبارت تو صیفی با مقادیر زبانی به یک رابطه ریاضی ساده تبدیل شده این تغییر ترکیب قواعد فازی را ساده تر می سازد.
در حقیقت سیستم فازی TSK یک میانگین وزنی از مقادیر بخش های انگاه قواعد می باشد.
مشکلات عمده سیستم فازی TSK عبارتند از:
1)بخش آنگاه قاعده یک فرمول ریاضی بوده و بنابراین چهارچوبی را برای نمایش دانش بشری فراهم نمی کند .
2)این سیستم دست ما را برای اعمال اصول اصول مختلف منطق فازی باز نمی گذارد و در نتیجه انعطاف پذیری سیستم های فازی در این ساختار وجود ندارد.
برای حل این مشکل ما از نوع سومی از سیستم های فازی یعنی سیستم های فازی با فازی سازها استفاده میکنیم.
به منظور استفاده ازسیستم های فازی خالص در سیستم های مهندسی یک روش ساده اضافه کردن یک فازی ساز در ورودی که متغییر هایی با مقادیر حقیقی را به یک مجموعه فازی تبدیل کرده و یک غیر فازی ساز که یک مجموعه فازی را به یک متغییر با مقدار حقیقی در خروجی تبدیل میکند می باشد .
نتیجه یک سیستم فازی با فازی ساز و غیر فازی ساز بوده که در شکل 5 نشان داده شده است.
این سیستم فازی معایب سیستم فازی خالص و سیستم فازی TSK رامی پوشاند.از این پس منظور ما از سیستم های فازی سیستم های فازی با فازی ساز و غیر فازی ساز خواهد بود.
سیستم های فازی کجا و چگونه استفاده می شوند؟
سیستم های فازی را می توان بعنوان کنترل کننده حلقه باز و یا کنترل کننده حلقه بسته مورد استفاده قرار داد .هنگامی که بعنوان کنترل کننده حلقه باز استفاده میشود سیستم فازی معمولا بعضی پارامترهای کنترل را معین کرده و انگاه سیستم مطابق با این پارامترها ی کنترل کار می کند.
بسیاری از کار برد های سیستم فازی در الکترونیک به این دسته تعلق دارند. هنگامی که سیستم فازی بعنوان یک کنترل کننده حلقه بسته استفاده میشود در این حالت خروجی های فرایند را اندازه گیری کرده و بطور همزمان عملیات کنترل را انجام میدهد .
کاربرد سیستم فازی در فرایندهای صنعتی به این دسته تعلق دارد.
منطق فازی روشی برای پردازش وقایع غیر قطعی ارائه میکند؛ دقیقا آنچه که در طبیعت و زندگی روزمره با آن در ارتباط هستم.
در منطق فازی با مقادیری غیر قطعی و تقریبی کار میکنیم؛ محدودهای از احتمالات که ممکن است اتفاق بیافتند.
منطق فازی در مقابل منطق باینری binary یا منطق Boolean قرار دارد.
منطق فازی برای طراحی سیستمهای خبره expert systems به کار میرود. سیستمهای خبره قوانین جهان واقع را شبیه سازی میکنند.
کنترل خودکار ترافیک، دوربینهای فیلمبرداری، ماشینهای لباسشویی هوشمند، سیستمهای تشخیص هویت از روی اثر انگشت یا تصویر مردمک چشم و غلط یاب تایپی در نرم افزارهای ویرایش متن مانند MS-Word از منطق فازی استفاده میکنند.
نارسایی منطق 0 و 1 برای شبیه سازی جهان واقعی را منطق فازی کاملا حل میکند. برای مثال در سیستم راننده خودکار اتومبیل، محاسبه و کنترل فاصله اتومبیل از کناره جدول یا اتومبیلهای دیگر با منطق باینری ممکن نیست و در این شرایط منطق فازی مشکل گشا خواهد بود. اگر رانندگی آموزش میدهید برای بیان فاصله بین اتومبیل و کناره جدول خواهید گفت: “تقریبا نیم متر”.
تنها روش برای گفتن چنین مقادیر غیر قطعی در سیستمهای کامپیوتری استفاده از منطق فازی است.
زمینه های تحقیق عمده در تئوری فازی
منظور ما از تئوری فازی تمام تئوری هایی است که از مفاهیم اساسی مجموعه های فازی یا توابع تعلق استفاده میکنند .تئوری فازی را به 5 شاخه عمده می توان تقسیم کرد .
1)ریاضیات فازی که در ان مفاهیم ریاضیات کلاسیک با جایگزینی مجموعه های فازی با مجموعه های کلاسیک تو سیه پیدا کرده است .
2)منطق فازی وهوش مصنوعی که در آن منطق کلاسیک تقریب هایی یافته و سیستم های (خبره) بر اساس اطلاعات و استنتاج تقریبی توسعه پیدا کرده است.
3)سیستم های فازی که شامل کنترل فازی و راه حل هایی در زمینه پردازش سیگنال و مخابرات می باشد. 4)عدم قطعیت و اطلاعات که انواع دیگری از عدم قطعیت را مورد تجزیه تحلیل قرار داده.
5)تصمیم گیری های فازی که مسائل بهینه سازی را با محدودیت های ملایم در نظر می گیرد .
مدل سازی
مدل ریاضی، گاه شامل مدل منطقی نیز میشود، به این واسطه که منطق هم جزئی از ریاضی است. در بیشتر موارد کیفیت پژوهش انجام شده کاملاً وابسته به دقت مدل ساخته شده است.
هرچه هم خوانی تئوریهای داده شده با نتایج تجربی بیشتر باشد، مدل بهتری ساخته شدهاست.
علم رباتیک برنامه آموزشی با دید تخصصی به رباتیک شامل آموزش زمینههایی از مهندسی برق، کامپیوتر و مکانیک است که در ساخت و استفاده از رباتها مورد نیاز هستند.
در این بخش به مدل سازی ربات A465 میپردازیم. مدل مورد نظر که در این قسمت ارائه می شود، شامل اصطحکاک کولومب میباشد. مدل سازی که در این گزارش انجام می شود از مرجع ]1[ اقتباس شده است که یک مقاله میباشد.
مدل استاندارد این سیستم در بسیاری از کتابهای کنترل و مدل سازی یافت میشوند اما در به دلیل تحریمها و یا گران بودن این کتب از مقالههای با کیفیت بالا کمک میگیریم. در مرجع ]1[ مدل کلی سیستم به صورت زیر درنظر گرفته شده است:
در رابطه فوق تابع اصطحکاک کولومب و ضریب اصطحکاک ویسکوزیته میباشد.
معادله دیفرانسیل فوق، یک فرم معروف رباتیکی است که برای توصیف رفتار یک ربات مورد استفاده قرار میگیرد. ضرایب این معادله دیفرانسیل به صورت زیر میباشند.
پارامترهای مورد نیاز برای شبیه سازی سیستم در جدول زیر آورده شده است:
…
همچنین داریم:…
و داریم:…
تا به اینجای کار مدل ریاضی سیستم مورد بحث در این مقاله توضیح داده شد. در ادامه مدل مورد نیاز باید به کد کامپیوتری تبدیل شود. با توجه به اینکه مدل سیستم پیچیده است، در این قسمت ما از کد سیمولینک برای شبیهسازی استفاده می کنیم.
در شبیه سازیهای ارائه شده از یک متلب فانکشن استفاده میکنیم. در صورتی که گشتاور ورودی یک نیوتونی به هر سه کانال سیستم حلقه بسته داده شود، خروجی به صورت شکل زیر خواهد بود.
شکل 1: خروجی سیستم حلقه باز با تحریک ورودی دلخواه و برابر با 1 نیوتنی
تابع نوشته شده در نرم افزار متلب به منظور مدلسازی سیستم به صورت زیر میباشد.
function q_dd=dynamic_model(z)
%%%%%
q=z(1:3);
q_dot=z(4:6);
T=z(7:9);
%%%%%%
q11=q(1);
q12=q(2);
q13=q(3);
%%%%%
q11_dot=q_dot(1);
q12_dot=q_dot(2);
q13_dot=q_dot(3);
%%%%%
ادامه کد را با خرید این پروژه خواهید دید.
سیستمهای فازی به عنوان شناساگر
در بسیاری از زمینهها سیستمهای فازی علاوه بر کنترل، وظیفه مدلسازی یک سیستم را نیز برعهده دارند. در این راستا الگوریتمهایی تعریف میشود که هدف آن الگوریتم، مدلسازی و درک درستی از رفتار سیستم است.
در بسیاری از موارد، کاربر با استفاده از دانشی که دارد رفتار سیستم را در ذهن بررسی کرده و به سیستم فازی اعمال میکند. این شیوه در روشهایی که از سیستم فازی به عنوان کنترل کننده استفاده میشود کارساز است و در بقیه موارد معمولا غیر ممکن است.
استفاده از الگوریتمهای مختلف از قبیل گرادیان نزولی، لونبرگ مارکوات و … معمولا روشهایی است که میتوان برای تعیین و تطبیق رفتار سیستم فازی با یک سیستم حقیقی به کار برد. در این پروژه از سیستم فازی به عنوان شناساگر رفتار ربات استفاده شده است.
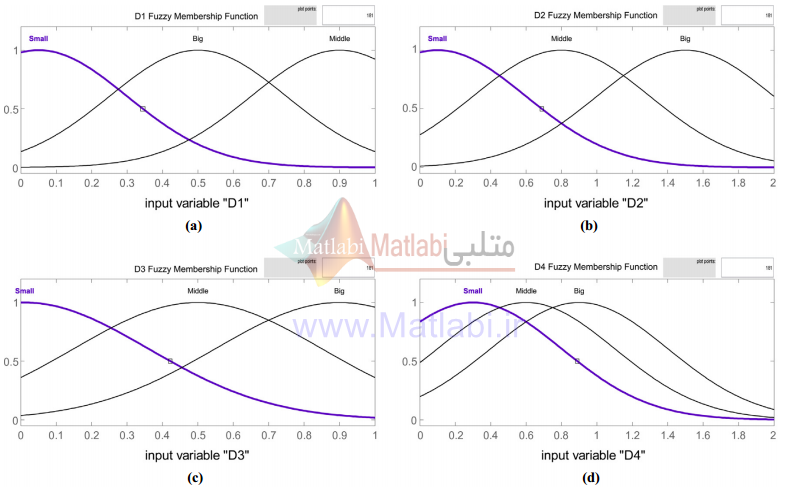
برای شناسایی سیستم مورد نظر، در مقاله چهار ورودی D تعریف شده است. برای این ورودیها، توابع تعلق به صورت زیر درنظر گرفته میشود.
شکل 2: توابع تعلق مربوط به ورودی سیستم
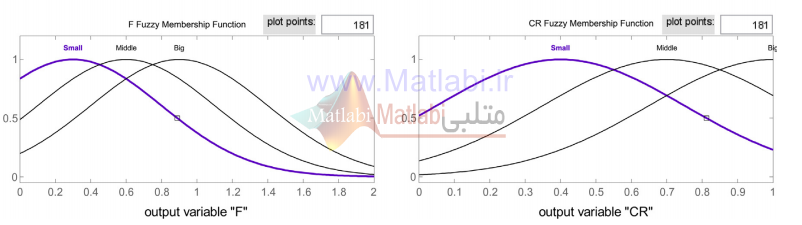
شکل 3: توابع تعلق خروجی سیستم فازی
جدول سیستم فازی داده شده به صورت زیر میباشد:
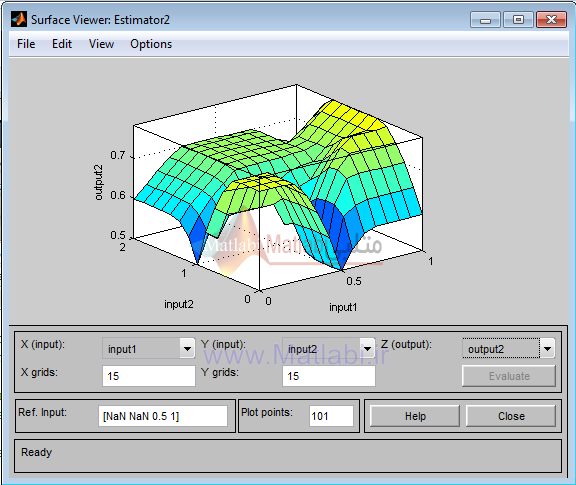
در نرم افزار متلب سیستم فازی مربوطه را تشکیل میدهیم. در واقع در این سیستم فازی ورودیهای D1 تا D4 میباشند که به صورت دو تایی نسبت به خروجی در ادامه رسم میشوند.
در واقع توجه داریم که سیستم داده شده یک سیستم غیر خطی است که میتوان ورودی و خروجیها را برحسب یکدیگر رسم کرد. اصولاً با رسم این ورودی و خروجیهای سیستم برحسب یکدیگر، میتوان به چگونگی رفتار سیستم فازی پی برد.
این رفتار در شکلهای 3 تا 8 نشان داده شده اند.
رسم D1 و D2 برحسب مقدار خروجی اول:
شکل 4: رسم ورودی های D1 و D2 در مقایسه با خروجی اول
رسم D1 و D2 برحسب مقدار خروجی دوم:
شکل 5: رسم ورودی های D1 و D2 در مقایسه با خروجی اول
به همین صورت می توان بقیه خروجیها را بر حسب ورودی ها رسم کرد. یکی از شناساگرهای غیرخطی شبکههای فازی میباشند که در این قسمت به طور مختصر به شرح این ابزار پرداخته میشود.
در عمل بسیاری از سیستمها غیرخطی هستند، که در بسیاری از کارهای عملی سیستم با استفاده از یک تابع تبدیل خطی حول نقطه کار مدل میشود که در این صورت با استفاده از یک کنترل کننده خطی کنترل میشود.
اما باید توجه داشت که در بعضی سیستمها به دلیل درجه غیرخطی گری بالای سیستم، با تغییر اندکی حول نقطه کار مدل خطی دیگر معتبر نبوده و کنترل کننده خطی در نقطه کار جدید با مشکل روبرو خواهد شد.
در اینجا استفاده از شبکههای فازی به عنوان ابزارهایی که از انعطافپذیری بالایی برخوردار هستند، مورد توجه قرار میگیرد.
همانطور که قبلا هم توضیح داده شد، در این راستا با استفاده از الگوریتمهای مشخصی به شناسایی یک سیستم غیر خطی توسط سیستم فازی پرداخته میشود.
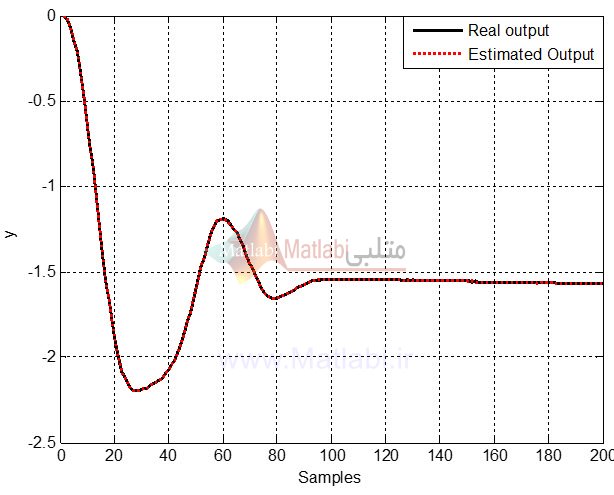
در این پروژه یکی از خروجیهای بازوی ربات توسط سیستم فازی شرح داده شده شناسایی میشود.
در واقع در مقالهای که به این منظور مورد بحث قرار گرفته شده است، سیستم فازی برای شناسایی یکی از بازوهای ربات مورد استفاده قرار گرفته شده است.
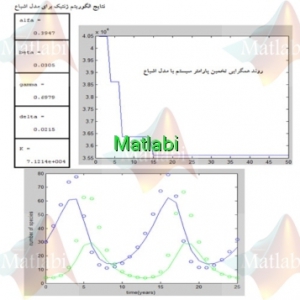
کدهای مربوط به این قسمت در شبیه سازیها آورده شده است که با اجرای آن داریم:
کلیدواژه: Robot manipulator, Adaptive differential evolution, Fuzzy logic, Parameter estimation, FADE algorithm, Parameter control, پروژه متلب,شبیه سازی بامتلب
شبیه سازی مقاله System identification and control of robot manipulator based on fuzzy adaptive differential evolution algorithm
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.






دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.