توضیحات
Robust static output feedback control for linear discrete-time systems with time-varying uncertainties
کنترل مقاوم سیستمهای خطی زمان گسسته دارای نایقینیهای پلی توپیک
- چکیده :
در این پروژه مقاله “Robust static output feedback control for linear discrete-time systems with time-varying uncertainties” که به بررسی موضوع کنترل مقاوم سیستمهای خطی زمان گسسته دارای نایقینیهای پلی توپیک پرداخته است، مورد مطالعه و شبیه سازی نتایج قرار گرفته است.
- توصیف سیستم :
سیستمهای گسسته-زمان خطی با نایقینیهای پلیتوپیک متغیر با زمان توسط روابط فضای حالت زیر توصیف می شوند:
که در آن بردار حالت، ورودی اغتشاش، ورودی کنترلی، خروجی اندازه گیری شده و خروجی کنترل شده است.
پارامتری نامعین ولی محدود و متغیر با زمان است که در رابطه زیر صدق میکند:
و
هدف در این مقاله طراحی کنترلر فیدبک خروجی با رابطه زیر است:
که منجر به سیستم حلقه بستهای با رابطه زیرگردد:
به طوری که سیستم فوق پایدار باشد و معیارعملکردهای بهینه یا تعیین شده ای را برآورده سازد.
- مروری بر کارهای انجام شده:
مسئله کنترل مقاوم سیستمهای خطی که عدم قطعیت های پلی توپیک دارند در دهه های اخیر توجه زیادی را به خود جلب کرده است و نتایج مهمی در این زمینه حاصل شده است .
یک روش حل چنین مسائلی”روش لیاپانوف” است.
در[3 و 10] از یک کاندید لیاپانوف برای تجزیه و تحلیل و نشر سیستمهای خطی غیر قطعی استفاده شده است.
اگرچه نتایج بدست امده محافظه کارانه می باشند.
این موضوع به دلیل استفاده از تنها یک تابع لیاپانوف برای کل محدوده عدم قطعیتها است.
به منظور غلبه بر این محافظه کاری در [1،2،4،6،7،8،11،12،14،17،19،20،21] روشهایی مبتنی بر استفاده از کاندیدهای لیاپانوف وابسته به پارامترها به کار گرفته شده است.
خصوصا روشهای جداسازی ماتریسهای لیاپانوف به وسیله ماتریسهای سیستم و با استفاده از یک متغیر اضافه در [1،11،17،19] به ترتیب برای سیستمهای گسسته و پیوسته قابل ذکرند.
در [21] و با متغیرات جزیی در نامساوی خطی ماتریسی (LMI) استاندارد که از Bounded Real Lemma ی پیوسته- زمان حاصل میشود، روشی به منظور طراحی کنترل کننده H_∞ برای سیستمهای پیوسته خطی که عدم قطعیتهای نامتغیر با زمان دارند، استخراج شده است.
علاوه بر آن، در [4،7] روشهای استفاده هم زمان از چندین متغیر اضافی برای سیستمهای با عدم قطعیتهای متغیر با زمان در پارامترها معرفی شده است که به ترتیب سیستمهای پیوسته و گسسته را در نظر میگیرند.
علاوه بر آن، D-پایداری مقاوم و طراحی فیلتر در [12،2،20،14] مد نظر قرار گرفته اند.
در تمامی روشهای طراحی اشاره شده، طراحی با فرض دسترسی کامل به حالتهای سیستم انجام شده است.
فرضی که در بسیاری از موارد عملی صادق نمیباشد.
در چنین مواردی استفاده از فیدبک خروجی لازم به نظر میرسد و در سالهای اخیر به این موضوع پرداخته شده است [5،13،15،16،18،22].
در میان روشهای فیدبک خروجی، روش فیدبک خروجی استاتیک با توجه کاربرد آسان و هزینه اندک مفید و کاربردیتر میباشد.
بسیاری ازمحققان فراوانی در سالهای اخیر به این موضوع پرداختهاند که [5،13،16،18،22] و مراجع آنها، منبع خوبی برای بررسی آن میباشد.
در [5]، شرایط LMI برای حل مسئله فیدبک خروجی استاتیک سیستمهای پیوسته و گسسته ارائه شده است.
در[22] یک رویکرد وابسته به پارامتربرای طراحی فیدبک خروجی استاتیک سیستمهای پیوسته-زمان ارائه شده است که هم زمان معیارهای عملکرد H_∞ و H2 را نیز برآورده میسازد.
در [13] نتایج این روش به سیستمهای گسستهای که عدم قطعیتهای تصادفی دارند توسعه داده شدهاند.
در [16] یک روش دو مرحلهای برای طراحی فیدبک خروجی استاتیک و دینامیک ارائه شده است که در گام اول آن یک کنترلر فیدبک حالت طراحی می شود و در گام دوم بهرهفید بک خروجی استاتیک به دست می اید.
در [18] با معرفی یک متغیر اضافی مستقل از پارامترها با ساختار زیر مثلثی، یک روش طراحی فیدبک خروجی استاتیک بر مبنای LMI برای سیستم های دارای عدم قطعیت های نا متغیربا زمان ارائه شده است.
این روشها به منظور طراحی کنترلر فیدبک خروجی استاتیک برای سیستمهای خطی با عدم قطعیتهای نا متغیر با زمان به کار گرفته میشوند و درصورتی برای حالت متغیر با زمان به کار میروند که تنها یک کاندید لیاپانوف درجه دوم استفاده شود.
اگرچه در روشهای ارائه شده در [5،13،18،22] بردار خروجی یا ورودی سیستم میباید ثابت باشند یعنی هیچ عدم قطعیتی نداشته باشند.
اگرچه روش [16] برای سیستمهایی که در آنها هم زمان ماتریس ورودی و خروجی دارای نایقینی هستند قابل استفاده است ولی طراحی آن وابسته به بهره به دست آمده در مرحله اول برای فیدبک حالت است.
روشهای محدب [Convex] محدودی برای طراحی کنترلر فیدبک خروجی مقاوم در حالتی موجود است که ماتریسهای ورودی و خروجی هم زمان دارای عدم قطعیتهای متغیر با زمان هستند.
از طرف دیگر، روش جداسازی ماتریس سیستم لیاپانوف از طریق تعریف متغیرهای اضافی، به صورت گستردهای در طراحی کنترلرهای فیدبک حالت سیستمهای خطی با عدم قطعیتهای پلیتوپیک به کار گرفته شده است و در شرایط طراحی کنترلر با محافظه کاری کمتر به دست آمده است.[2،12،14،20،4،7،21،11،1،19،17]
در مقاله تحت بررسی، این روش به کار گرفته شده است و در طراحی کنترلر فیدبک خروجی استاتیک برای سیستم های خطی دارای نایقینیهای متغیر با زمان توسعه داده شده است و شرایط کافی جدیدی در قالب پاسخ دستهای از LMI ها برای طراحی کنترلر فیدبکخروجی استاتیک ارائه شده است.
برخلاف مطالعات موجود، متغیر اضافی وابسته به پارامتربا ساختار پایین مثلثی در این تحقیق ارائه شده است که وابسته به خصوصیات ماتریسهای ورودی و خروجی سیستم است و در استخراج نتایج با محافظه کاری کمتر استفاده میشود.
علاوه برآن ، این روش می تواند در مورد سیستمهایی که نایقینیهای پلیتوپیک هم زمان در ورودی و خروجی دارند، نیز قابل کاربرد است.
- مقدمات مورد نیاز:
تعریف1:
- فرض کنید سیستم (1) پایدار مجانبی باشد.
- نرم H2 سیستم (1) به صورت زیر تعریف میشود:
که در آن و نویز سفید با متوسط صفر و ماتریس کوواریانس واحد است.
- فرض کنید سیستم (1) پایدار مجانبی باشد و برای هر رابطه زیر را داشته باشیم:
در این صورت نرم H_∞ سیستم کمتر از خواهد بود.
لم1: اگر ماتریسهای متقارن و ای وجود داشته باشد که :
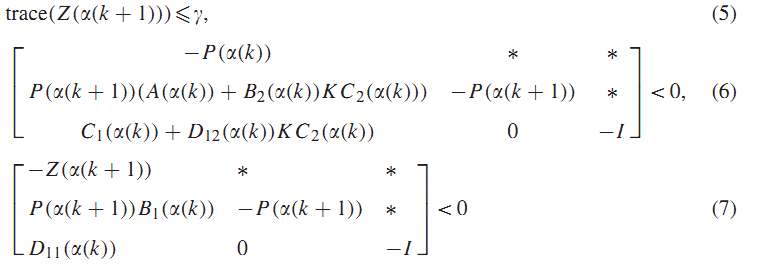
لم2: اگر ماتریس متقارن ای وجود داشته باشد بطوری که
که در ان
در این صورت نرم H_∞ سیستم (1) کمتراز خواهد بود.
اثبات:
قرار میدهیم . با انتخاب کاندید لیاپانوف از (8) داریم:
در این صورت سیستم(1) با پایدار مجانبی است.
رابطه زیر را در نظر بگیرید:
که در آن
با ا عمال لم مکمل شور (Schur complement Lemma) داریم :
که (9) را برای همه مقادیر تضمین می کند. علاوه بر آن :
از آنجایی که ، نامساوی فوق بیان میکند که (4) صادق است.
بنابراین نرم H_∞ سیستم (3) کمتر از است.
- طراحی کنترلر فیدبک خروجی استاتیک مقاوم:
در این قسمت دو روش برای طراحی کنترلر فیدبک خروجی استاتیک مقاوم دردو حالت مختلف ارائه شده است.
در حالت اول ها با رتبه کامل و در حالت دوم ها با رتبه کامل در نظر گرفته می شوند.
5-1 : حالت اول ( ها دارای رتبه کامل باشند)
در این قسمت فرض شده است ها دارای رتبه کامل باشند و ماتریسهای ای وجود دارند، به نحوی که:
در ادامه، با در نظر گرفتن فرض فوق ابتدا روشی برای طراحی کنترلر پایدار ساز فیدبک خروجی ارائه میشود که سپس برای طراحی کنترلر H_∞ وH2 توسعه داده میشود.
نکته1: برای هر ، متناظر یکتا نیست و یک حاص را میتوان از رابطه زیر به دست آورد:
که در آن پایهای عمود برای فضای پوچی است.
-
-
- : طراحی کنترلر مقاوم پایدار ساز
-
لم 3: اگر ماتریسهای متقارن و ماتریس های ، وجود داشته باشد که در رابطه (12a) یا (12b) صدق کنند:
سیستم (3) با ، از طریق قانون کنترل فیدبک خروجی پایدار مقاوم خواهد بود.
قضیه1: اگر ماتریسهای متقارن و ماتریس های ، وجود داشته باشد که به صورت
و در رابطه (18a) یا (18b) صدق کند:
سیستم(1) با توسط فید بک خروجی
پایدار مجانبی خواهد بود.
اثبات:
با توجه به ساختار و (10) و(19) خواهیم داشت:
که در آن
با جانشینی رابطه فوق به جای L در (18a) خواهیم داشت:
که نشان میدهد رابطه (12a) صادق است.
با استفاده از از لم 3 ثابت می شود که سیستم (3) پایدار مجانبی است.
اثبات از طریق (18b) نیز به طریق مشابه انجام می گیرد.
نکته: در قضیه (1)، دو شرط کافی برای طراحی فیدبک خروجی استاتیک مقاوم برای سیستمهای گسسته زمان با عدم قطعیت های نامتغیر با زمان پیشنهاد شده است و شرایط طراحی تحت قالب یک سریLMI بیان شده است.
اگر متغیرهای و و به ازا در قضیه 1 و ماتریسهای خروجی به ازا قرار دهیم، شرایط قضیه 1 تبدیل به نتایج (18) می شوند.
البته از روش های (5،22،13،16،18) نیز می توان به منظور طراحی کنترل کننده فیدبک خروجی برای سیستم های با ماتریس متغیر بهره برد که مقایسه این نتایج در قسمت 4 آورده شده است.
در اینجا لازم به تذکر است که برای هر ، های مختلفی وجود دارد که (10) را برآورده میسازد.
قضیه زیر نشان میدهد که شرایط قضیه 1 مستقل از انتخاب است.
قضیه2 :اگر شرایط قضیه 1 برای ای که (10) را برآورده میسازد برقرار باشد، این شرایط برای هر ای (10) را برآورده سازد نیز برقرار خواهد بود.
5-1-2- کنترل H_∞ وH2
در این قسمت نتایج به دست آمده برای پایداری مقاوم به کنترل H_∞ وH2 توسعه داده می شود:
قضیه3: اگر ماتریس های متقارن و ماتریس های ، وجود داشته باشد با
که در (24a) یا (24b) و ((25 و (26) صدق کند:
در این صورت قانون کنترلی فیدبک استاتیک خروجی (2)، نرم H2 سیستم را کمتر از قرار می دهد و بهره k از رابطه زیر به دست می اید :
اثبات: اگر قرار دهیم با استفاده از تکنیک قضیه 1 و از(24a) خواهیم داشت :
از ضرب (27) در و جمع داریم:
اگر تعریف کنیم رابطه (28) مانند رابطه (6) خواهد بود. از طرف دیگر با ضرب از چپ و راست (25) در
و ترانهاده آن خواهیم داشت
از ضرب (29) در و جمع آنها رابطه (7) با
به دست می آید.
به صورت مشابهی از (26) می توانیم به رابطه (5) برسیم.
با استفاده از لم 1 ، ثابت می شود که نرم H2 سیستم کمتر از خواهد بود.
به طریق مشابهی می توان از رابطه (24a) به اثبات صورت قضیه رسید.
قضیه زیر شرایط کافی برای طراحی کنترل کننده مقاوم H_∞ فیدبک خروجی استاتیک به دست می دهد:
قضیه 4: اگر ماتریس های متقارن و ماتریس های ، وجود داشته باشد
وجود داشته باشند که در روابط (30a) یا (30b)صدق کنند:
قانون کنترلی فیدبک استاتیک خروجی نرم H_∞ کمتر از را برای سیستم (3) به دست می دهد.
اثبات: با استفاده از لم 2 و مشابه قضیه 3 اثبات می شود.
نکته: مشابه آنچه در مورد قضیه 2 وجود داشت، برقراری شرایط قضیه 3 و 4 مستقل ازانتخاب می باشد.
5- 2 : حالت دوم ( ها دارای رتبه کامل باشند)
در این قسمت فرض بر آن است که ها دارای رتبه کامل هستند و ماتریس های وجود دارند که در رابطه
صدق می کنند.
نکته: مشابه آنچه در حالت اول دیدیم، هایی که در (31) صدق کنند یکتا نیستند.
یک خاص که از آن استفاده میشود از رابطه زیر بدست میآید :
که در ان نشان دهنده یک پایه متعامد برای فضای پوچی است.
لم 4 : اگر ماتریسهای متقارن و ماتریسهای وجود داشته باشند که در روابط a33 ویا b33 صدق کنند :
سیستم (3) با از طزیق کنترل فیدبک استاتیک خروجی پایدار مقاوم خواهد بود.
اثبات :
اگر a33 برقرار باشد خواهیم داشت :
با ضرب a33 در و حمع روی ها خواهیم داشت :
از (34) و (35) خواهیم داشت :
با ضرب (36) از چپ و راست در و ترانهاده آن بدست میآید :
با ضرب (37) در و و جمع آنها و استفاده از استنباطی مشابه آنچه در لم 3 داشتیم ، نتیجه قضیه اثبات میشود.
اثبات با فرض b33 نیز به طریق مشابه انجام میگیرد.
قضیه 5 : اگر ماتریسهای متقارن و ماتریسهای با
وجود داشته باشند که در روابط a38 ویا b38 صدق کنند :
سیستم (1) با از طریق کنترل فیدبک استاتیک خروجی با بهره پایدار مجانبی خواهد بود.
قضیه6 : اگر شرایط قضیه 5 برای ای که (31) را برآورده میسازد برقرار باشد، این شرایط برای هر ای که (31) را برآورده سازد نیز برقرار خواهد بود.
6 – مثالها :
مثال 1 : سیستم (1) با ماتریس ضرایب زیر را در نظر بگیرید :
که در آن میباشد.
با توجه به اینکه است، روش های مطرح در [5و22و13و16و18] و قضایای 1و 5 برای طراحی کنترل پایدارساز فابل استفاده اند.
پس از اعمال این روشها به منظور بدست آوردن حداکثر قابل دستیابی نتایج زیر حاصل شده اند :
مشاهده میشود در حالیکه روش [5] قابلیت حل این مثال را ندارد ، روش قضیه 1 و [18] نتایج مشابهی به دست میدهند و کمترین محافظه کاری را در روش قضیه 5 داریم.
مثال 2 : سیستم (1) با ماتریس ضرایب زیر را در نظر بگیرید :
با توجه به اینکه و است، روش های مطرح در [5و22و13و18] برای طراحی کنترل پایدارساز فابل استفاده نیستند درحالیکه از قضایای 1و 5 و روش [16] میتوان بهره برد.
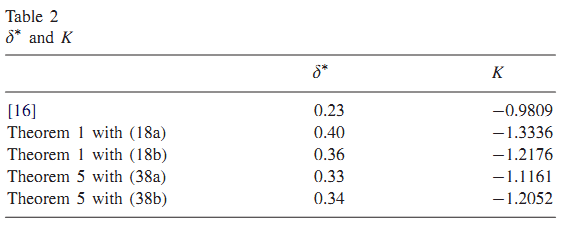
نتایج این روشها در پایدارسازی سیستم در جدول زیر خلاصه شده است :
مقایسه نتایج وجود محافظه کاری کمتر در استفاده از قضایای 1 و 5 را نشان میدهد.
مثال 3 : سیستم (1) با ماتریس ضرایب زیر را در نظر بگیرید :
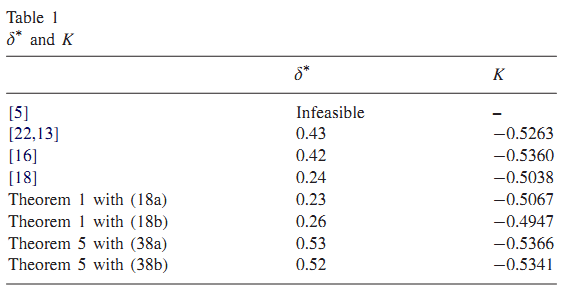
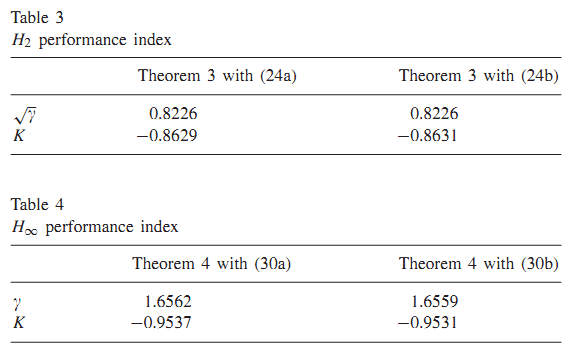
هدف در این مثال که مثال اصلی این مقاله نیز هست، طراحی کنترل کننده بهینه و برای سیستم فوق با استفاده از قضایای 3 و 4 میباشد.
نتایچ بدست آمده از این روش در جدول زیر خلاصه شده اند :
5 – شبیه سازی :
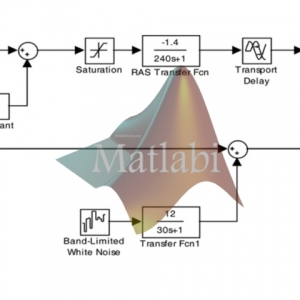
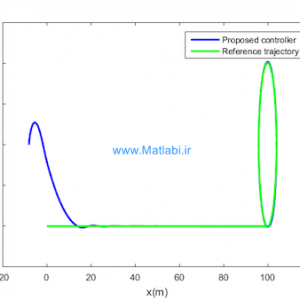
با توجه به اینکه مثال 3 مثال اصلی این مقاله و طراحی کنترل کننده بهینه و برای سیستم فوق با استفاده از قضایای 3 و 4 ، مثالی از کار اصلی انجام شده در این مقاله میباشد، در این قسمت با پیاده سازی شرایط این قضایا در نرمآفزار متلب به شبیه سازی و حل مثال فوق پرداخته ایم.
بدین منظور کدهای پیوست برای پیدا کردن حداقل نرم قابل حصول نوشته شده و با استفاده از آنها در محیط متلب ابتدا شرایط قضیه 3 بررسی شده، مقادیر متغیرها که در LMI های بیان شده صدق میکنند بدست آورده شده اند و بر اساس آنها بهره فیدبک خروجی و حداقل نرم قابل حصول بدست آمده است که در جدول زیر با نتایج مقاله مقایسه شده اند :
| نتایج شبیه سازی | نتایج مقاله | |
| 0.8512 | 0.8226 | Radical Y |
| -0.7211 | -0.8629 | K |
جدول 5
در قسمت دوم شرایط قضیه 4 بررسی شده، مقادیر متغیرها که در LMI های بیان شده صدق میکنند بدست آورده شده اند و بر اساس آنها بهره فیدبک خروجی و حداقل نرم قابل حصول بدست آمده است که در جدول زیر با نتایج مقاله مقایسه شده اند :
| نتایج شبیه سازی | نتایج مقاله | |
| 1.5845 | 1.6562 | Radical Y |
| -0.9630 | -0.9537 | K |
جدول 6
با توجه به شبیهسازیهای انجام شده مشاهده میشود که اگرچه با توجه به ابزارهای موجود مناسب در حل LMI ها روش پیشنهادی روشی مناسب در طراحی کنترلر بهینه و برای سیستمهای پلیتوپیک است ولی، باید در نظر داشت که تعداد بالای نامعادلات ماتریسی خطی موجود در شرایط قضایای مطروحه باعث افزایش حجم محاسبات و احتمال خطا میشود(در حقیقت برای یک سیستم با نایقینی پلیتوپیک Nتایی، LMI برای کنترلر و LMI برای کنترلر میباید که بررسی شوند.).
کلید واژه : کنترل مقاوم, پروژه متلب, پروژه matlab , شبیه سازی با متلب
Discrete-time systems, Static output feedback, Time-varying uncertainty, Robust control, Linear matrix inequalities (LMIs), Parameter dependent Lyapunov function
شبیه سازی
Robust static output feedback control for linear discrete-time systems with time-varying uncertainties
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.


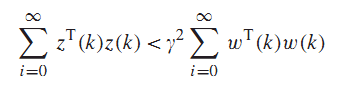
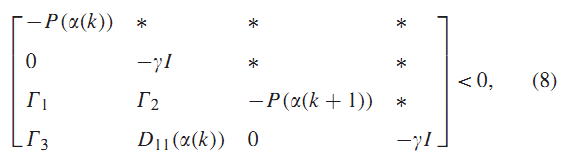
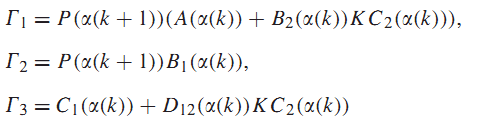
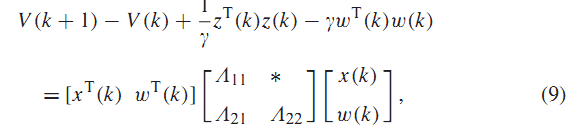
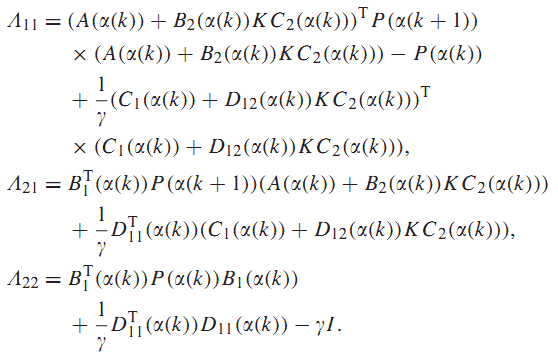
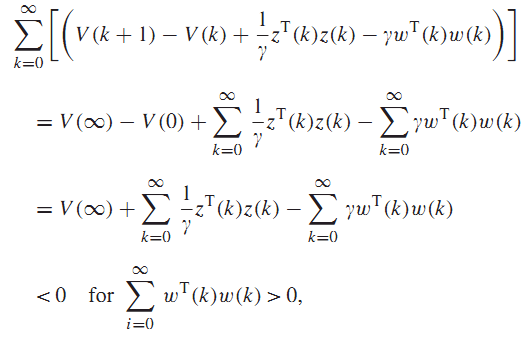
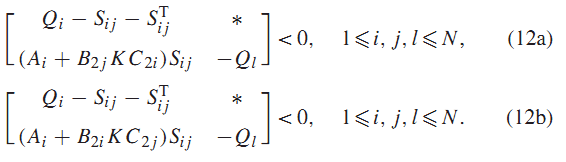
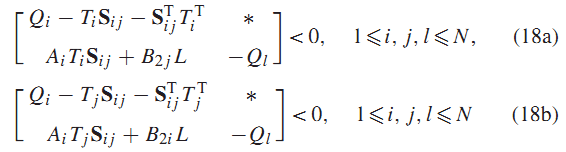
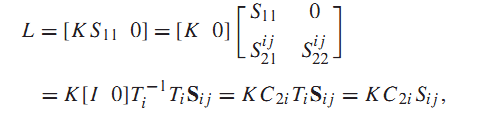
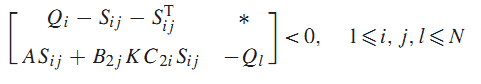
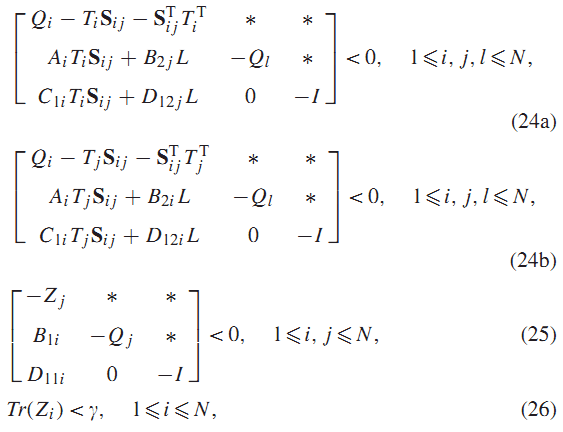
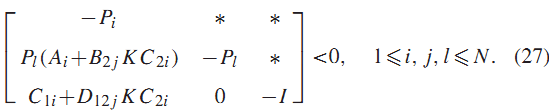
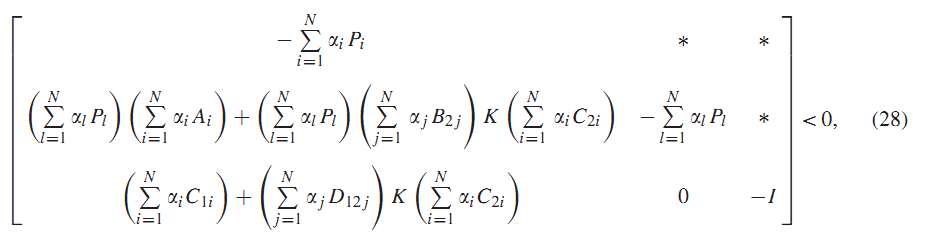
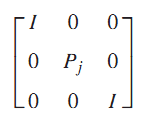
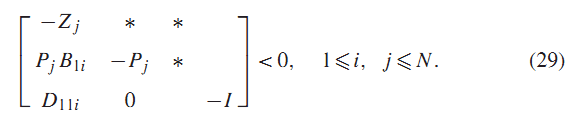
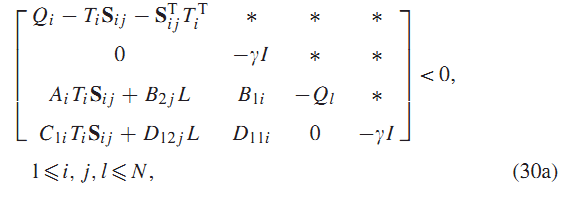
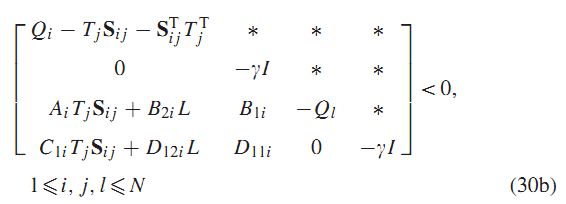
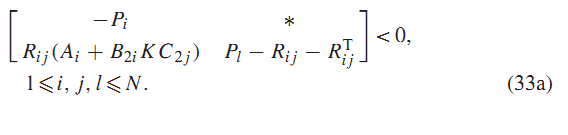
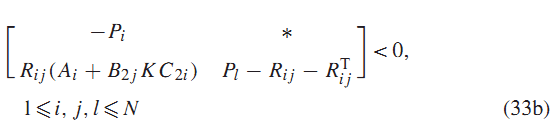
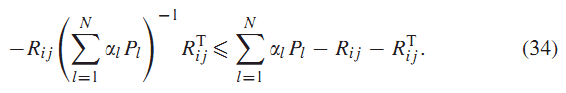
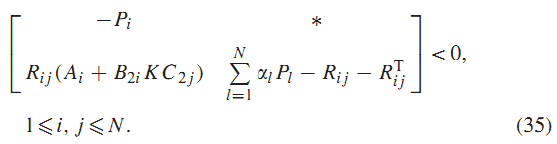
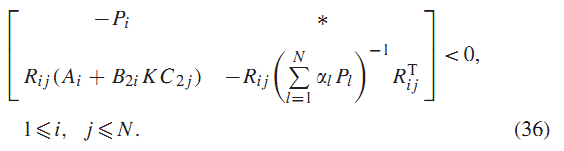
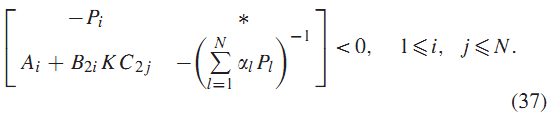
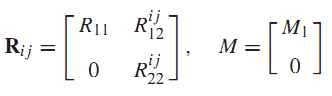
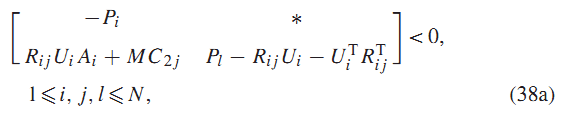
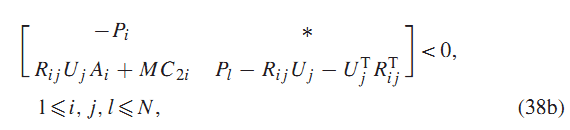
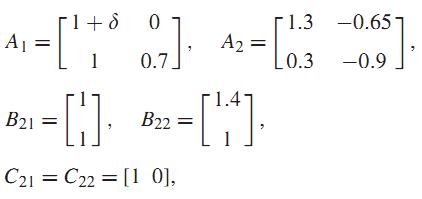
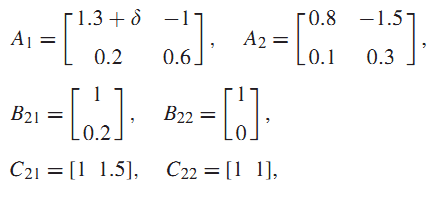
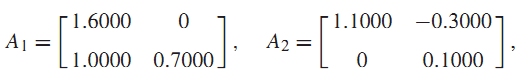
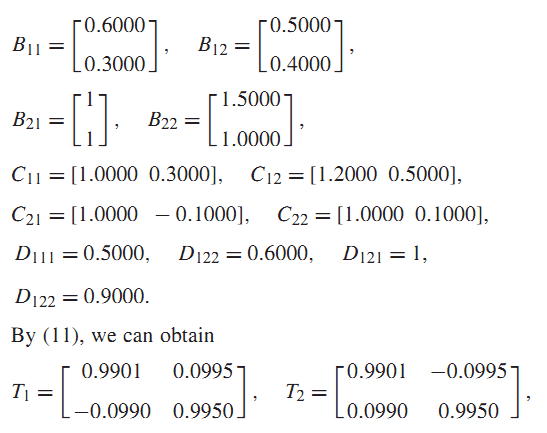



دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.