توضیحات
Robust Multivariable PI Control
ترجمه فارسی موضوع مقاله: کنترل PI چند متغیره مقاوم
کنترل PI چند متغیره مقاوم ; کاربرد در کنترل فرایند
چکیده:
دراین مقاله کاربرد یک تکنیک توسعه یافته جدید “انتگرالگیر مشروط“ برای تنظیم خروجی طبقه ای از سیستم های غیرخطی به سیستم کنترل فرایند را بررسی خواهیم کرد.
کنترل کننده ما به یک کنترل کننده نوع PI/PID اشباع شده به طور خوبی سازگار با یک ساختار ضد انحلال کاهش می یابد.
این یک مفهوم ویژه است زیرا مادامی که کاربرد ترفندهای کنترل غیرخطی مانند خطی سازی با فیدبک، کنترل تطبیقی/عصبی و کنترل پیش بین مدل غیرخطی رشد قابل توجهی در سیستم های صنعتی دارد، شیوه صنعتی به تواتر به کنترلرهای PI/PID استناد می کند.
با این طراحی، ما هم نتایج تنظیم سراسری تحت فیدبک حالت (زمانی که نیازی به محدود شدن کنترل نیست) و هم نتایج محلی/ نیمه سراسری با کنترل اشباع شده و تحت فیدبک خروجی را فراهم می کنیم.
زمانی که این طراحی را برای مسائل کنترل فرایند مختلف به کار بردیم، با وجود اطلاعات جزئی از پارامترهای Plant ، نتایج شبیه سازی نشان داد که عملکرد ردیابی خوبی بدست آمده است.
کلمات کلیدی: کنترل فرایند، تنظیم خروجی، کنترل انتگرالی، کنترل لغزشی
مزایای روش گفته شده نسبت به کنترل کننده های PI/PID در شیوه صنعتی حاضر:
- ساختار ساده یعنی سادگی در محاسبات
- قابلیت دستکاری محدودیت
- مقاوم سازی در مقابل عدم قطعیت پارامترها و کلاسهای معینی از اغتشاشات خارجی
- عدم نیاز به حالت کامل (یعنی طراحی کنترل فیدبک خارجی)
ما معتقدیم که این روش مخصوصا برای کاربردهای واقعی مناسب است.
قصد داریم عملکرد این روش را برای کنترل واکنش راکتور تانک با اختلاط کامل (CSTR) و از طریق شبیه سازی روش نشان دهیم.
بخش های بعدی مقاله به شرح زیر است:
بخش دوم : توصیف سیستم تحت بررسی، فرضها و اهداف کنترلی و طراحی کنترل موجود و نتایج تحلیلی اصلی
ما کنترل u را برای تنظیم خطای e به صفر طراحی می کنیم و سپس به یک فرض شبه مینیمم فاز برای تضمین کرانداری z استناد می کنیم.
طراحی ما مبتنی بر ترکیب عمل انتگرال با صورتی پیوسته از کنترل مد لغزشی (SMC) است.
در مورد فیدبک حالت ما i امین سطح لغزشی را به صورت زیر تعریف می کنیم:
بخش سوم : کاربرد روش برای یک مثال CSTR)) تک ورودی تک خروجی (SISO ) با درجه نسبی 2
بخش چهارم : بررسی نتایج برای یک سیستم MIMO
بخش پنجم : نتیجه گیری
توصیف سیستم و طراحی کنترل:
یک سیستم غیرخطی MIMO با بردار یکنواخت با درجه نسبی
ρ = {ρ1 , ρ2 , . . . , ρm} قابل تبدیل به فرم نرمال خطای زیر فرض کنید:
که ei ∈ Rρi بردار خطا در خروجی yi و مشتقاتش تا مرتبه ρi−1 است.
z دینامیک داخلی و r(ρi)i (t) مشتق ρi ام از i امین ترکیب مرجع
d = (rss , θ , wss) که rss ∈ Rm مقدار مرجع بردار حالت ماندگار است و θ یک بردار از پارامترهای ناشناخته ثابت وابسته به یک مجموعه فشرده Θ است.
wss سیگنال خارجی ( برون زا ) حالت ماندگار است .
ν(t) و ˜ w(t)به ترتیب انحراف سیگنال مرجع و سیگنال خارجی از مقادیر حالت ماندگارشان هستند. و جفت (Ai ,Bi) یک فرم کانونیکال کنترل پذیر و بیان کننده یک سلسله از ρi انتگرال گیری است
ما کنترل u را برای تنظیم خطای e به صفر طراحی می کنیم و سپس به یک فرض شبه مینیمم فاز برای تضمین کرانداری z استناد می کنیم.
که σi خروجی رابطه زیر است :
که > 0 ki0 و ثابتهای مثبت طوری انتخاب شده
و μi پارامتر مثبت کوچک که عرض لایه مرزی i ام را مشخص می کند.کنترل به صورت زیر داده شده است:
که Aˆ یک ماتریس ناویژه معلوم است
طراحی ما مبتنی بر ترکیب عمل انتگرال با صورتی پیوسته از کنترل مد لغزشی (SMC) است.
در مورد فیدبک حالت ما i امین سطح لغزشی را به صورت زیر تعریف می کنیم:
: برا ی حذف هر عبارت نامی(کم ارزش) معلوم در s˙ و v برای کرانداری عبارات باقیمانده در آن.
انتخاب توابع βi در بخش چهارم مقاله Seshagiri and Khalil, 2005 مشخص شده است.
کنترل (4) می تواند از طریق جایگزینی eij , ، مشتق (j-1) ام ei1 ، با e^ij (تخمین زده شده اش) بدست آمده با استفاده از مشاهدات گین بالا(HGO) به حالت فیدبک خروجی توسعه یابد.
که εi>0 و ثابتهای مثبت αij طوری انتخاب شده اند که ریشه های چند جمله ای زیر بخشهای حقیقی منفی داشته باشد:
پارامترهای μi از جایگزینی یک SMC ایده آل با تقریب پیوسته اش بدست می آیند و بنابراین بهتر است که جهت بهبود عملکرد SMC ایده آل به اندازه کافی کوچک انتخاب
شوند.
به طور مشابه در کنترل کننده فیدبک خروجی جهت بهبود عملکرد تحت فیدبک حالت ، εi پارامترهای مشاهده گین بالا بهترست به اندازه کافی کوچک انتخاب شوند…….
پارامترهای میزان سازی εi و μi : ابتدا μi به تدریج کاهش پیدا می کند تا زمانی که پاسخ گذرای فیدبک حالت جزئی به اندازه کافی به SMC ایده آل نزدیک شود که شامل انتگرالگیر نیست.
سپس به تدریج εi کاهش پیدا میکند تا زمانی که پاسخ گذرای تحت فیدبک خروجی به اندازه کافی به فیدبک حالت نزدیک شود.
برای سیستم SISO انعطاف پذیری که دسترسی به انتخاب توابع ˆ F و β است میتواند جهت ساده سازی کنترل (3) به کار برده شود.
این طراحی ویژه مادامیکه ساختار ساده ای دارد همچنین بدیهی است اگر کنترل باید کراندار باشد.
+
زیرا از (6) مشتقات خطا تا مرتبه ρ−1 در کنترل ظاهر می شود، کنترلر یک کنترلر PIDρ−1 ضد انحلال و نتیجه شده از اشباع است.
در مورد درجه نسبی ρ = 1 و ρ = 2 کنترل (6) به سادگی یک کنترلر PI/PID اشباع شده وفق یافته (میزان) ضد انحلال است.
معرفی راکتور :
رآکتور شیمیایی دستگاهی است که در آن واکنش یا واکنش های شیمیایی نظیر تبدیل، ترکیب یا تجزیه به منظور تولید مواد مورد نظر انجام می شود.
طبق قرارداد دستگاهی که در آن واکنش سوختن به منظور تولید انرژی انجام می شود، رآکتور نیست.
« تقسیم بندی رآکتورها»
از مهمترین مشخصه های واکنش های شیمیایی تعداد و نوع فازهایی است که واکنش در آن صورت می گیرد:
- رآکتورهای تک فازی:
در این رآکتورها واکنش در فاز گاز یا در فاز مایع انجام می شود
- رآکتورهای چند فازی:
در این رآکتورها واکنش میان فازهای گاز و مایع یا میان دو فاز مایع یا میان فازهای سیال و جامد انجام می شود.
انواع دیگر تقسیم بندی:
واحدي (Stage wise)
ديفرانسيلي(Differential)
راکتورهاي واحدي(Stage wise)
در اين نوع راکتورها شرايط در تمام حجم سيستم به صورت يکنواخت باقي مي ماند.
اگر از هر نقطه راکتور نمونه برداري کنيم، از نظر ترکيب نسبي و دما يکسان است و هيچ تفاوتي ندارد و موازنه جرم و انرژي رادر تمام راکتور برقرار مي نماييم.
راکتورهاي ديفرانسيلي (Differential)
شرايط درهرنقطه از راکتور يکسان نبوده و به صورت ديفرانسيلي تغيير مي کند.
ممکن است با زمان تغيير ننمايد، ولي از هر نقطه به نقطه ديگر متفاوت است.
براي برقراري موازنه جرم و انرژي بايد يک جزء ديفرانسيلي در نظر گرفت.
تفاوت راکتورهاي واحدي و ديفرانسيلي اين است که در راکتورهاي ديفرانسيلي بين غلظت ورودي و خروجي، تمام مقادير را داريم ولي در راکتورهاي واحدي نمي توانيم غلظت را به طور پيوسته داشته باشيم و غلظت به طور پله اي تغيير مي کند.
تقسیم بندی دیگر رآکتورها براساس نوع عملیات آن ها است. این تقسیم بندی به شکل زیر است:
1) رآکتورهای ناپیوسته (Batch Reactors)
2) رآکتورهای پیوسته یا جریان پایدار (Continuous or Steady Flow Reactors)
3) رآکتورهای نیمه پیوسته (Semi Batch Reactors)
راکتورهای ناپیوسته (Batch) :
در يک راکتور ناپيوسته ورود و خروج جرم وجود ندارد.
از ديدگاه تاريخي راکتورهاي ناپيوسته از آغاز صنعت شيميايي مورد استفاده بوده است و هنوز هم به صورت وسيعي در توليد مواد شيميايي با ارزش افزودني بالا نظير دارو سازي مورد استفاده مي باشد.
در این رآکتورها مواد اولیه به مقدار معین وارد رآکتور می شود، در زمان مشخص واکنش انجام می گیرد و سپس محصول از راکتور خارج می شود.
بدین ترتیب یک دوره کار که شامل بارگیری، انجام واکنش و تخلیه است پایان می پذیرد و راکتور برای انجام واکنش در دوره بعد پاکسازی و آماده می شود.
این نوع راکتورها نسبتا ساده هستند و احتیاج به وسایل کمکی و سیستم های کنترل کمتری دارند.
در صنعت از این نوع راکتورها برای انجام واکنش های کند، که احتیاج به زمان اقامت زیادی دارند، استفاده می شود.
مدت اقامت واکنش دهنده ها در داخل راکتور، که طی آن واکنش گرها فرصت انجام واکنش پیدا می کنند، زمان اقامت گویند.
در یک راکتور ناپیوسته کامل (ايده آل) اختلاف درجه حرارت یا غلظت در درون حجم سیستم وجود ندارد.
بعلت انجام واکنش، غلظت با زمان تغییر خواهد نمود، ولی در هر لحظه در تمام نقاط یکسان خواهد بود.
سرعت واکنش نیز یکسان و در تمام نقاط برابر با سرعت متوسط سیستم می باشد.
امتياز راکتورهاي ناپيوسته (Batch) در اين است که با دادن زمان لازم براي انجام واکنش مواد اوليه با درصد تبديل بالا به محصولات موردنظر تبديل مي گردند. در حالي که استفاده از اين نوع راکتورها محدود به واکنش هاي متجانس فاز مايع مي باشد.
از ديگر محدوديت هاي اين نوع راکتورها بالا بودن هزينه توليد در واحد حجم محصول توليد شده مي باشد.
همچنين توليد صنعتي در مقياس بالا در اين گونه راکتورها مشکل است.
رآکتورهای پیوسته:
در این نوع راکتورها، مواد اولیه به طور دایم وارد راکتور می شود و پس ار انجام واکنش محصول، پیوسته از راکتور خارج می شود.
این گونه راکتورها هنگامی در صنعت استفاده می شوند که هدف تولید مقدار زیادی محصول باشد در ضمن راکتورهای پیوسته برای انجام واکنش های سریع مناسب تر می باشند.
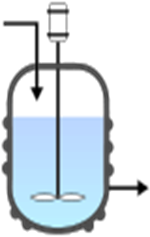
CSTR : در یک راکتور پیوسته (Flow Reactor) اگر اختلاط ایجاد شده توسط همزن به اندازه کافی سریع باشد، در راکتورهاي اختلاط کامل به علت وجود داشتن همزن خوراک ورودي به سرعت در سرتاسر ظرف پراکنده شده و غلظت در هر نقطه تقریبا برابر با غلظت متوسط خواهد شد .
بنابراین سرعت واکنش در هر نقطه تقریبا یکسان می شود .
همچنین غلظت خروجی با غلظت داخلی برابر خواهد بود.
به این نوع راکتور یک مخلوط کن کامل (Perfect Mixer) با چگالی ثابت گفته می شود.
در فرهنگ مهندسی شیمی به چنین وسیله ای عموما CSTR ، یا مخلوط کن کامل یا صرفا یک راکتور با اختلاط کامل اتلاق می شود.
CSTR در شرايطي که يک واکنش شيميايي احتياج به همزدن شديد داشته باشد مورد استفاده قرار مي گيرد.
CSTR يا به تنهايي و يا به صورت پشت سرهم متصل مي گردند. کنترل حرارتي در اين نوع راکتورها به آساني انجام مي گيرد.
يکي از محدوديتهاي اين نوع راکتورها درصد تبديل پايين در مقايسه با ساير راکتورها مي باشد.
به همين دليل حجم راکتور مذکور بايد بزرگ انتخاب شود، تا به درصد تبديل بالا دست يافت.
راکتورهاي Mixed يا CSTR براي اغلب واکنش هاي متجانس در فاز مايع استفاده مي شود.
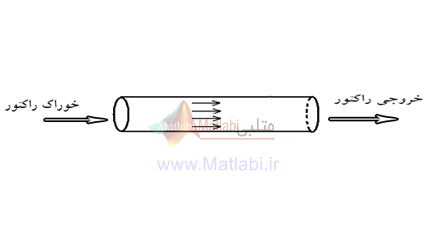
راکتورهاي لوله اي ( Plug، راکتور با جریان قالبی)
در صنايع شيميايي براي فرايند هاي با مقياس بزرگ معمولآ از راکتورهاي لوله اي استفاده مي شود.
زيرا نگهداري سيستم راکتورهاي لوله اي آسان مي باشد (چون داراي قسمتهاي متحرک نيستند) ومعمولا بالاترين درصد تبديل مواد اوليه در واحد حجم راکتور را در مقايسه با ساير راکتورهاي سيستم جاري دارا هستند.
از محدوديت اين نوع راکتورها مشکل حرارتي براي واکنشهاي گرمازاست که بسيار سريع عمل ميکنند و نهايتآ منجر به تشکيل نقاط داغ (Hot Spot) مي گردند. اغلب واکنشهاي متجانس گازي در اين نوع راکتورها انجام مي گيرند.
غلظت واکنشگرها مسلما در طول لوله تغییر خواهد کرد.
چنين سيستمهايي توزيع شده (Distributed) ناميده مي شوند و تجزيه تحليل معادله عملکرد آنها در شرايط پايدار مستلزم حل معادلات است.
در جريان Plug سرعت کليه ذرات يکسان است.
هيچ ذرهاي از ذره ديگر سبقت نمي گيرد و عقب هم نمي ماند.
راکتورهاي دوره اي (Recycle Reactor)
در اين نوع راکتور مخلوط واکنش خروجي از راکتور بدون عبور از مراحل جدا سازي و بازيافت به ورودي راکتور برگشت داده مي شود.
اين نوع برگشت در راکتور Mixed وجود دارد و از اين نظر امري عادي مي باشد.
يعني استفاده از جريان برگشتي براي يک راکتور Mixed اثري روي بازدهي ندارد.
بايد توجه داشت که استفاده از جريان برگشتي براي يک راکتور با جريان Plug معمولآ بازدهي را کاهش مي دهد و آن را به سمت بازدهي يک راکتور Mixed سوق مي دهد.
لذا معمولآ در شرايط زير از راکتورهاي دوره اي استفاده مي کنيم:
1-براي واکنشهاي اتوکاتاليزوري و واکنشهايي که احتياج به همزن خاصي دارند.
مثلآ اگر واکنشي احتياج به درصد معيني از همزن (کمتر از الگوي اختلاط راکتور مخلوط شونده و بيشتر از الگوي اختلاط در راکتور لوله اي) داشته باشد از راکتور دوره اي استفاده مي کنيم.
2-براي واکنشهايي که بايد در شرايط هم دما انجام بگيرند.
3-براي واکنشهايي که متشکل از چند واکنش سري يا موازي رقابتي هستند، براي رسيدن به توليد بهينه (ماکزيمم) از محصول مورد نظر (Selectivity)، از راکتورهاي دوره اي استفاده مي کنيم.
راکتورهاي دوره اي (Recycle Reactor)
در اين نوع راکتور مخلوط واکنش خروجي از راکتور بدون عبور از مراحل جدا سازي و بازيافت به ورودي راکتور برگشت داده مي شود.
اين نوع برگشت در راکتور Mixed وجود دارد واز اين نظر امري عادي مي باشد. يعني استفاده از جريان برگشتي براي يک راکتور Mixed اثري روي بازدهي ندارد.
بايد توجه داشت که استفاده از جريان برگشتي براي يک راکتور با جريان Plug معمولآ بازدهي را کاهش مي دهد و آن را به سمت بازدهي يک راکتور Mixed سوق مي دهد.
لذا معمولآ در شرايط زير از راکتورهاي دوره اي استفاده مي کنيم:
1-براي واکنشهاي اتوکاتاليزوري و واکنشهايي که احتياج به همزن خاصي دارند. مثلآ اگر واکنشي احتياج به درصد معيني از همزن (کمتر از الگوي اختلاط راکتور مخلوط شونده و بيشتر از الگوي اختلاط در راکتور لوله اي) داشته باشد از راکتور دوره اي استفاده مي کنيم.
2-براي واکنشهايي که بايد در شرايط هم دما انجام بگيرند.
3-براي واکنشهايي که متشکل از چند واکنش سري يا موازي رقابتي هستند، براي رسيدن به توليد بهينه (ماکزيمم) از محصول مورد نظر (Selectivity)، از راکتورهاي دوره اي استفاده مي کنيم.
رآکتورهای نیمه پیوسته:
این نوع راکتورها دارای انواع متنوعی هستند.
در نوع متداول آن یکی از مواد اولیه ابتدا در داخل راکتور بارگیری و سپس به تدریج ماده یا مواد اولیه دیگر به آن اضافه می شود.
در نوع دیگر مواد اولیه به طور هم زمان وارد راکتور می شود ولی تا پایان واکنش هیچ ماده ای از راکتور خارج نمی شود.
نوع دیگری از آن وجود دارد که یکی از مواد اولیه در داخل راکتور بارگیری شده است و ماده دیگر به تدریج به آن اضافه می گردد و همزمان با آن محصول نیز از راکتور خارج می شود.
دلایل استفاده :
1- یک ماده اولیه در معرض واکنشهای مختلفی، یکی بعد از دیگری قرار دارد. بنابراین استفاده از یک ظرف آسانتر است و اساسا هر واکنش مستقل از دیگری است.
2- در حین عمل پر کردن به محض اینکه واکنشگرها با هم تماس پیدا کنند واکنش شروع می شود.
بر حسب اینکه واکنشگر گرها بطور دنبال هم وارد شوند یا به طور همزمان ، محیط اولیه واکنش تفاوت خواهد کرد.
3- جهت کنترل توزیع ترکیب درصد فرآورده ها، یک واکنشگر در فواصل زمانی کوتاه وارد راکتور می شود .
4-جهت اجتناب از محدودیت تعادلی، یکی از فراورده ها عمدا از راکتور خارج می شود.
5-بعضی از واکنشگرها به میزان ناچیزی در محیط واکنش حل می شوند و اگر به طور مداوم به ظرف اضافه نشوند تمام خواهند شد.
مباحث کنترلی :
چند جمله ای هرویتز: چند جمله ای که تمام مقادیر ویژه آن اکیدا سمت چپ باشد.
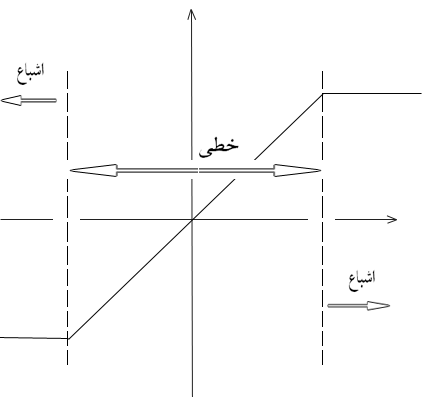
اشباع:
هنگامی که ورودی یک سیتم فیزیکی افزایش یابد، غالبا پدیده زیر مشاهده می شود:وقتی که ورودی کوچک است، افزایش آن منجر به افزایش متناظر خروجی می شود (غالبا به صورت تناسبی) ؛ اما هنگامیکه ورودی به سطح خاصی می رسد، افزایش بیشتر آن، افزایش کمی در خروجی ایجاد میکند ( و یا افزایشی در خروجی ایجاد نمی کند.)
خروجی به سادگی حول مقدار بیشینه اش باقی می ماند.
هنگامیکه این اتفاق می افتد، گفته می شود که سیستم در اشباع است.
وقوع اشباع باعث کاهش بهره وسیله، هنگامیکه ورودی افزایش پیدا کند، میشود.
کنترل مقاوم :
در طراحي سيستم هاي كنترل عموماً با فرض داشتن مدل نسبتاً دقيق از سيستم به تحليل و بررسي سيستمها مي پردازيم.
اين مدل ها عمدتاً پس از خطي سازي معادلات غير خطي حول نقاط مختلف كار بدست مي آيند.
اما چنانچه مدل سيستم دچار تغييراتي شود و عوامل ناخواسته و غير قابل پيش بيني بر سيستم اثر گذارد مسلماً كنترلر طراحي شده از درجه اعتبار ساقط خواهد بود.
بديهـي است كه در يك روش طراحي عملـي و واقع بينانه ، بايستي اين نامعيني ها و تغييرات كه سيستم بدون شك در عمل با آن روبرو خواهد بود در مدل سيستم منظور شده باشد، تا بتوان با وجود عدم قطعيت ها در مدل و ايجاد تفاوت در مدل نامي و مدل واقعي سيستم به طراحي كنترلر پرداخت.
كنترلر هاي مقاوم اين خواسته را برآورده خواهد ساخت.
بنابراين كنترل مقاوم عبارتست از كنترل سيستم ها با ديناميك غير قطعي و يا در معرض اغتشاشات نامعين يا ورودي هاي نامعلوم و خطاهاي مدل سازي بوسيله كنترل كننده هاي ثابت بصورتي كه پايداري و عملكرد مقاوم در آن حاصل آيد .
تعاریف:
به خاصيت ويژه اي كه يك سيستم كنترل بايستي داشته باشد، تا در محيط واقعي عملكرد مطلوبي داشته باشد، پايداري مقاوم مي گوئيم و اگر كنترل كننده به صورتي طرح گردد، كه سيستم بر روي تمام مدل هاي مجموعه پايدار باشد، سيستم پايدارمقاوم مي باشد.
عملكرد مقاوم :
عبارتست از برقراري اهداف عملكردي سيستم حلقه بسته در حضور انواع قطعيت ها و اختلالات معين، هدف نهايي يك سيستم كنترل مقاوم اينست كه سيستم در برابر تغييرات محيط واقعي يا بروز عدم قطعيت هاي مدل پايدار باشد.
انواع عدم قطعیت ها در سیستم:
1-عدم قطعيت پارامتري (عدم قطعیت در پارامترهای مدل )
2ـ عدم قطعيت ساختاري (دینامیکهای مدل نشده، مربوط به عدم دقت در مرتبه سیستم)
اگر كنترل كننده بتواند مشخصه هاي عملكرد، از قبيل رديابي حالت ماندگار وروي مرجع ، حذف اغتشاش و شرايط سرعت پاسخ را برروي همه مدل هاي مجموعه بر آورده نمايد، گوئيم سيستم داراي عملكرد مقاوم است.
مسئله طراحي ، به صورتيكه شرايط پايداري و عملكرد مقاوم بر آورده شوند مسئله كنترل مقاوم ناميده مي شود.
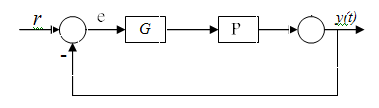
شرط عملکرد نامی
جهت ردیابی ورودی توسط خروجی لازمست که تابع تبدیل از r به e دامنه خیلی کمی داشته باشد. اگر این تابع تبدیل را با S نمایش دهیم
لازمست که دامنه S از ε کمتر باشد یعنی ε > ∞||S|| پس 1 > ∞||S . 1/ ε ||
اگر 1/ ε دامنه تابع تبدیل W1 باشد جهت ردیابی بهتر در بازه خواسته شده باید مقدار W1 در آن بازه بزرگ باشد
||W1S||<1
شرط پایداری مقاوم : P~=P(1+∆W2)
W2 : تابع تبدیل پایدار با دامنه صعودی(با افزایش فرکانس عدم قطعیت افزایش می یابد. W2 تابع تبدیلی است که حالتهای مختلفی که سیستم ممکن است داشته باشد را می پوشاند.) و 1>∞ || ∆|| و P , P~ قطبهای ناپایدار مشابهی دارند
||W2T||<1
شرط عملکرد مقاوم
|| |W1S|+ |W2T| || < 1
که
S+T=1
T=L / (1+L)
یک روش ساده برای کنترل مقاوم ، چیزی است که اصطلاحا روش شناسی کنترل لغزشی نامیده می شود. به طور شهودی این روش مبتنی است بر این نکته که بسیار آسانتر است که سیستم های مرتبه اول را کنترل کنیم (یعنی سیستم هایی که با معادلات دیفرانسیل مرتبه اول توصیف شده اند) چه غیر خطی باشند چه نامعین تا اینکه سیستم های عمومی تر مرتبه n ام را .
بخشی از گزارش اینجا نیامده و با خرید این محصول دریافت خواهید کرد.
سطوح لغزشی :
سیستم دینامیکی تک ورودی زیر را در نظر بگیرید:
که در آن اسکالر x خروجی موردنظر (مثلا وضعیت یک سیستم مکانیکی )، اسکالر u ورودی کنترل (مثلا گشتاور موتور) و
بردار حالت اند.
در معادله بالا تابع f(X) (در حالت غیرخطی کلی) دقیقا معلوم نیست ولی میزان عدم دقت بر روی f(X) با یک تابع پیوسته معلوم از X محدود شده از بالاست. به طور مشابه بهره کنترل b(X) دقیقا معلوم نیست ولی علامت آن معلوم بوده و به وسیله یک تابع معلوم پیوسته از X محدود شده است. مسئله کنترل این است که حالت X را چنان بیابیم که یک حالت متغیر با زمان مشخص را با وجود خطا در f(X) و b(X) تعقیب کند.
برای اینکه وظیفه ردیابی با استفاده از یک کنترل محدود u قابل دستیابی باشد، حالت اولیه مطلوب Xd (0) بایستی طوری باشد که: =X(0) Xd (0)
مثلا در یک سیستم مرتبه دوم موقعیت یا سرعت نمی تواند جهش داشته باشند، به طوریکه هر مسیر دلخواه عملی از لحظه t=0 لزوما از موقعیت و سرعتی مشابه پلان شروع می شود .
یک ساده سازی نمادی :
بگذارید خطای ردیابی در متغیر x به صورت باشد و فرض کنید :
بردار خطای ردیابی است.
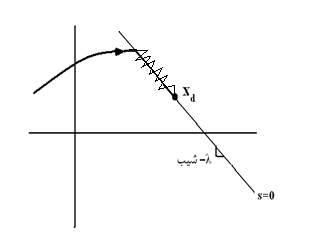
بعلاوه اجازه دهید یک سطح متغیر با زمان S(t) در فضای حالت R(n) با معادله اسکالر =0 s(x,t) تعریف کنیم که :
و λ یک ثابت اکیدا مثبت است. یعنی بطور ساده s یک جمع وزن دار از خطای موقعیت و خطای سرعت است.
با داشتن شرط اولیه =X(0) Xd (0) مسئله ردیابی معادل باقی ماندن بر روی سطح S(t) است.
در حقیقت بیانگر یک معادله دیفرانسیلی است که، با فرض شرایط اولیه ، حل یکتایی آن
است .
لذا مسئله ردیابی بردار n بعدی Xd را می توان به مسئله حفظ کمیت اسکالر s در صفر تقلیل داد.
به طور دقیق تر مسئله ردیابی n بعدی Xd را می توان با مسئله پایدار سازی مرتبه اول در s جایگزین کرد.
این مسئله مرتبه اول حفظ اسکالر s در صفر را می توان حالا با انتخاب قانون کنترل u معادله طوری بدست آورد که خارج از S(t) :
شرط لغزشی:
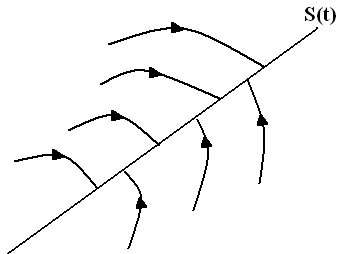
در این رابطه η ثابت اکیدا مثبت است. اساسا این معادله بیان می کند که مربع فاصله تا این سطح همچنانکه با s2 اندازه گیری شده، در امتداد تمامی مسیرهای سیستم کاهش می یابد . لذا شامل مسیرهایی است که به سمت سطح S(t) هستند، همانطور که در شکل زیر نشان داده شده است.
به طور خاص وقتی که بر روی این سطح قرار بگیرید مسیرهای سیستم بر روی آن باقی می مانند .
به طور خلاصه ایده پشت معادلات و
اینست که تابع کاملا خوشرفتاری از خطای ردیابی s مطابق برداشته و سپس قانون کنترل پسخوردی u در
را چنان انتخاب کنیم که s2 علیرغم عدم دقت در مدل و آشفتگیها یک تابع لیاپانوف باقی بماند.
پس از آن دستورالعمل طراحی کنترل کننده شامل دو مرحله است:
اول قانون کنترل u پسخوردی چنان انتخاب می شود که شرط لغزشی برقرار باشد .
اما برای اینکه عدم دقت در مدلسازی و آشفتگیها محسوب شوند، قانون کنترل بایستی بر روی S(t) ناپیوسته باشد .
چونکه پیاده سازی کنترل سوئیچینگ مربوطه لزوما ناقص است این باعث لرزش می شود.
لرزش در عمل مطلوب نیست زیرا باعث فعالیت کنترلی زیادی میشود و نیز ممکن است دینامیکهای فرکانس بالایی (مانند حالتهای ساختاری مدل نشده، تاخیرهای صرفنظر شده و …) را که که در هنگام مدلسازی صرفنظر شده اند، تحریک کند.
لذا در مرحله دوم قانون کنترل ناپیوسته u به طور مناسبی همواره شده تا تعادل بهینه ای بین پهنای باند کنترل و دقت ردیابی به دست آید: در حالی که مرحله اول عدم قطعیت پارامتری محسوب می شود، مرحله دوم مقاوم بودن نسبت به دینامیکهای مدل نشده فرکانس بالا را کسب می کند.
یک مثال اساسی : سیستم مرتبه دوم زیر را در نظر بگیرید:
که در آن uورودی کنترل ، x خروجی موردنظر و دینامیکهای f (احتمالا غیرخطی یا متغیر با زمان) دقیقا معلوم نیست ولی مانند تخمین زده شده است.فرض می شود خطای تخمین بر روی یک تابع معلوم
محدود شده است:
برای اینکه سیستم را تعقیب کند ، یک سطح لغزشی s=0 مطابق
تعریف می کنیم.
یعنی :
آنگاه داریم :
لذا بهترین تقریب قانون کنترل پیوسته که بتواند
را بدست آورد عبارتست از :
اما برای اینکه شرط لغزشی علیرغم عدم قطعیت در دینامیکهای f، برقرار باشد، بر روی سطح s=0 یک جمله ناپیوسته به اضافه می کنیم:
با انتخاب در
طوری که به اندازه کافی بزرگ باشد، می توانیم تضمین کنیم که شرط لغزشی برقرار است. در حقیقت :
طوری که با فرض k= F+η خواهیم داشت:
حال سوال اینست که چگونه قوانین کنترل را بدست آوریم که سیستم را نزدیک سطح s=0 حفظ کنیم و در عین حال از کلیه لرزشها پرهیز کند.
تقریبهای پیوسته قوانین کنترل سوئیچینگ:
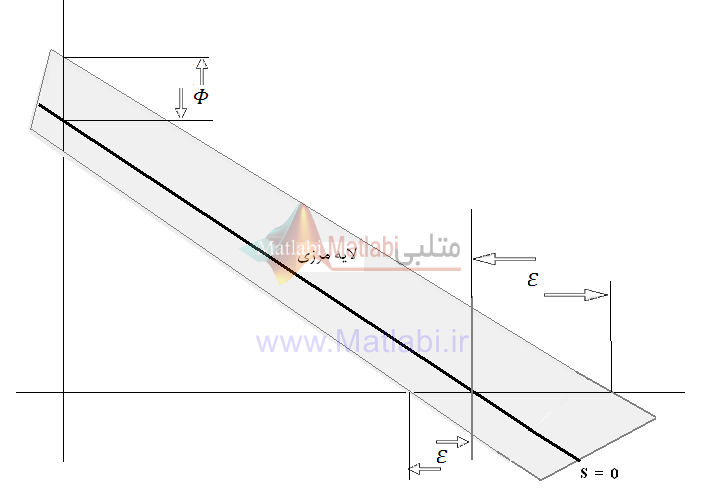
در حالت کلی برای اینکه عملکرد کنترل کننده به طور مناسب باشد، بایستی لرزش حذف شود. این کار می تواند با هموار کردن ناپیوستگی کنترل در یک لایه مرزی باریک از همسایگی سطح سوئیچینگ
که در آن Φ ضخامت لایه مرزی و ε = Φ / λn-1 پهنای لایه مرزی است، بدست اید، همانند شکل زیر که برای n=2 نشان داده شده است:
به عبارت دیگر خارج از B(t)، قانون کنترل u را مانند قبل (یعنی با برقراری شرط لغزشی) انتخاب می کنیم ، که تضمین می کند لایه مرزی جاذب است. تمامی مسیرهایی که درون B(t=0)شروع شوند، برای همه t ≥0 درون B(t) باقی می مانند.
و سپس u را در B(t) درون یابی می کنیم. برای مثال درون B(t) در عبارت u جمله sgn(s)را با s/Φ جایگزین می کنیم. این به ردیابی با دقت تضمین شده ای در حدود ε (به جای ردیابی کامل) منتهی می شود .
که :
SISO CSTR:
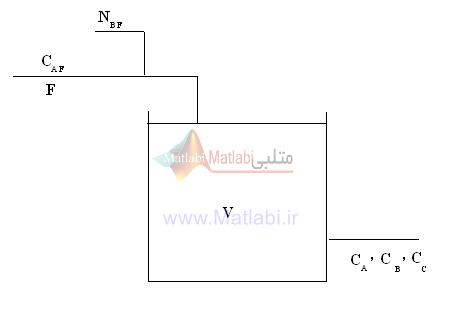
یک راکتور تانک همزن پیوسته را برای یک واکنش شیمیایی در حال انجام چند مولفه ای همدما و در فاز مایع در نظر بگیرید.
واکنش شیمیایی سیستم به صورت روبروست:
یک واکنش جانبی مرتبه اول مدل نشده از B وجود دارد.
مطلوب ما کنترل تا حد امکان نزدیک CC به مقدار حالت پایدار با تنظیم سرعت تغذیه مولی B (NBF) است.
معادلات مدلسازی برای این سیستم به شرح زیر است:
که:
u = NBF / (F*CAF)
CA: غلظت A در واکنش
CB : غلظت B در واکنش
CC : غلظت C در واکنش
CAF : غلظت تغذیه A
F : سرعت تغذیه حجمی
V: حجم راکتور
x1: غلظت نرمالیزه شدهA : CA/CAF
x2: غلظت نرمالیزه شده B : CB/CAF
x3: غلظت نرمالیزه شده C : CC/CAF
ki : ثابتهای سرعت مرتبه اول
NBF : سرعت تغذیه مولی B
Dai : شرایط Damköhler نسبی برای واکنشها :
Da1 =k1V/F
Da2=k2VCAF/F
Da3=k3VCAF/F
سیستم درجه نسبی 2 دارد : ρ=2 ؛ و برای هر خروجی ثابت دلخواه سیستم یک نقطه تعادل منحصر به فرد
دارد : و یک ورودی تعادل
دارد .
همانطور که قبلا تعیین شد، هدف کنترلی دستکاری سرعت تغذیه نرمالیزه شده u برای تنظیم y در یک مقدار ثابت دلخواه است. فرض می کنیم ضرایب Damköhler ناشناخته اند و پارامترهای ناشناخته بردار θ را تشکیل می دهند.توجه کنید که فرمولاسیون سیستم ما برای تطبیق با عدم قطعیت های ممکن وابسته به حالت و حتی اغتشاشات خارجی تغییرپذیر با زمان تصویب شده است. با تغییر متغیر زیر سیستم به فرم نرمال خطا تغییر شکل می یابد (فرم 1):
معادلات (6) کنترلر PID اشباع شده :
که k0 , k1 >0 . از آنجایی که به طور نمونه e2 اندازه گیری نشده است، ما را با تخمینش
که با استفاده از مشاهده گر گین بالا بدست آمده است جایگزین می کنیم.
توجه کنید که حتی وقتی x2 اندازه گیری شده است، به پارامتر ناشناخته Da3 وابسته است.
که ε>0 است و ثابتهای α1وα2طوری انتخاب شده اند که ریشه های چندجمله ایλ2+α1λ+α2=0 بخشهای حقیقی منفی داشته باشد.
جهت شبیه سازی این سیستم ما مقادیر عددی تعیین شده در مرجع Scaratt , [2000] را جهت کمک به مقایسه با نتایج آن انتخاب می کنیم:
Da1=3.0 , Da2=0.5 , Da3=1.0
و تصور کنید که پایداری سیستم در مقدار خروجی مطلوب اتفاق می افتد که برای این انتخاب مقادیر تعادل زیر را داریم:
همینطور انتخاب کرده ایم:
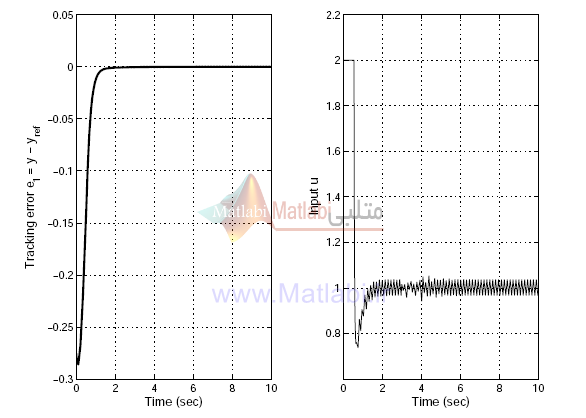
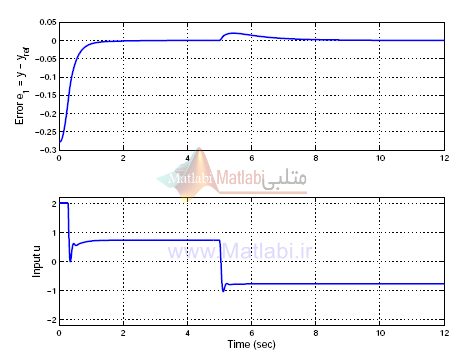
شکل زیر خطای e1 و ورودی u را برای مقادیر بالا نمایش می دهد. وجود پدیده سریع ضربه زدن در u یکی از نتایج مقدار کوچک μ است.
در فقدان کنترل انتگرالی ما نیاز داریم جهت خطای حالت ماندگار کوچک ، μ را کوچک فرض کنیم.
یعنی یک μکوچکتر در عین حال که منجر به خطای حالت ماندگار کوچکتری می شود اما هزینه کنترل سریع ضربه زنی (تصادم ، chattering) را نیز به دنبال خواهد داشت.
یکی از نتایج کاربرد کنترل انتگرالی اینست که نیازی نداریم که μ را جهت کاهش خطای حالت ماندگار کوچک فرض کنیم بلکه فقط به انداز کافی جهت پایداری اغتشاش – نقطه تعادل وابسته کوچک فرض می شود.
جهت مصور سازی موضوع ما شبیه سازی قبلی را با μ=1 تکرار می کنیم.
شکل بعدی نتایج شبیه سازی را نشان می دهد و میبینیم که خطای حالت ماندگار هنوز در کنترل انتگرالی صفر است اما حالا هیچ تصادمی در کنترل وجود ندارد.
برای مقایسه ما نشان داده ایم خطا و ورودی را برای یک SMC پیوسته بدون عمل انتگرالی یعنی
با مقادیر عددی مشابه برای k1 , k و μ .
توجه کنید که اینجا هیچ تصادمی در کنترل وجود ندارد زیرا که μ کوچک نیست.
اما حالا خطای حالت ماندگار غیرصفر است. بدون کنترل انتگرالی کاهش μ خطای حالت ماندگار را کوچکتر می کند، اما دوباره به پدیده تصادم منجر خواهد شد.
نتایج گزارش شده بالا قیاس پذیرند یعنی پاسخ های گذرا حداقل در مقایسه با Scaratt , [2000] خوبست درحالیکه
بخشی از گزارش اینجا نیامده و با خرید این محصول دریافت خواهید کرد.
بالاخره، به منظور نمایش تصویری مقاوم بودن کنترلر برای هر دوی عدم قطعیت و اغتشاش تطبیق یافته، ما شبیه سازی قبلی را با مقادیر عددی ضرایب Damköhler تغییر یافته تکرار می کنیم به صورت:
Da1=3.5 , Da2=0.2 , Da3=1.5
همینطور فرض می کنیم که یک ورودی اغتشاش جمع پذیر به صورت
δ(t)= 1.5 Π(t-5)وجود دارد.
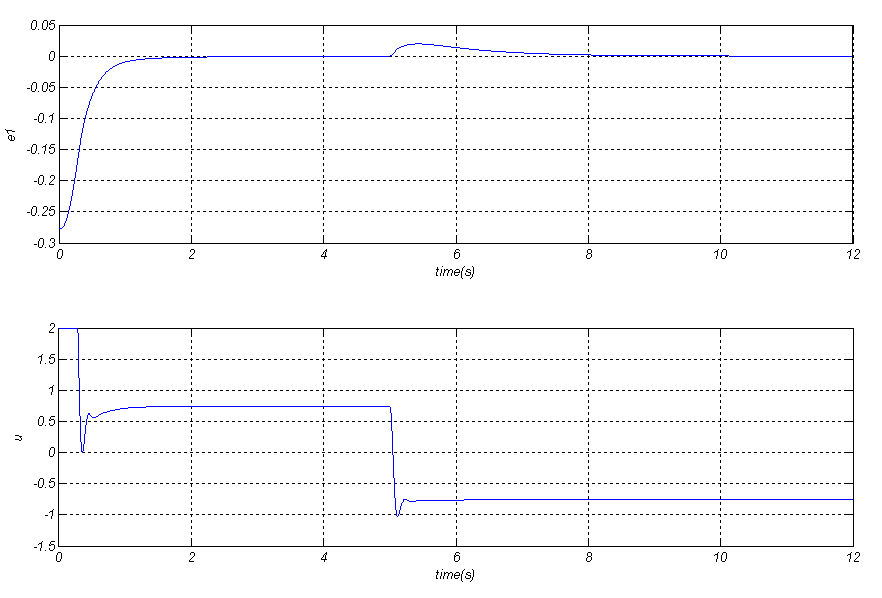
همه مقادیر قبلی از شبیه سازی قبلی حفظ شده اند به جز μ=0.2 .نتایج شبیه سازی در شکل زیر نمایش داده شده است.
و مشهود است که تنظیم خوب با کنترلر فیدبک خروجی با وجود عدم قطعیتهای پارامتری و اغتشاشات بدست آمده است.
شکلهای بدست آمده از شبیه سازی با اجرای فایلهای
CSTR1d,CSTR1e,CSTR1f
شکلهای موجود در مقاله
به جهت تایید کار ، یادآوری می کنیم که این کنترلر یک کنترلر PID اشباع شده با خاصیت ضد انحلال با انتخاب خاصی از گینهای کنترلر است .
شبیه سازی بالا مقاوسازی در مقابل عدم قطعیتهای پارامتری و اغتشاشات را با ورودی های مقید و فقط با کاربرد فیدبک خروجی نشان میدهد.
همینطور فرض می کنیم که یک ورودی اغتشاش جمع پذیر به صورت
δ(t)= 1.5 Π(t-5)وجود دارد.همه مقادیر قبلی از شبیه سازی قبلی حفظ شده اند به جز μ=0.2 .نتایج شبیه سازی در شکل زیر نمایش داده شده است.
و مشهود است که تنظیم خوب با کنترلر فیدبک خروجی با وجود عدم قطعیتهای پارامتری و اغتشاشات بدست آمده است.
:MIMO CSTR
در بخش قبلی، کنترل یک سیستم SISO را فرض کردیم.
مثال بعدی ما پلیمریزاسیون (ترکیب و تراکم ذرات) رادیکال(بنیادی) آزاد MIMO مربوط به methyl methacrylate در یک CSTR با حجم ثابت گرمازا است.
حلّال ethyl acetate خواهد بود، زمانی که راکتور benzoyl peroxide است.
در مقاله Kurtz [2000] معادلات مدل به شرح زیرند:
که S,I,T,M به ترتیب غلظت تکپار، دمای راکتور، غلظت اولیه و غلظت حلال اند. V حجم راکتور است . Sf , If , Mf به ترتیب غلظت تغذیه تکپار، اولیه و حلال هستند.Tf دمای تغذیه ، q سرعت جریان تغذیه
Tf دمای سرد کننده و
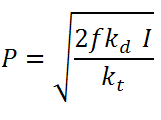
f ضریب آغازگر و kt ثابت سرعت انتهایی هستند.
ثابتهای سرعت kp, kd از دمای وابستگی آرینوس پیروی می کنند یعنی :
زمانی که عبارت kt با استفاده از ضریب همبستگی Ray-Schmidt اثر چسبندگی به صورت زیر محاسبه شده است:
که:
که و Vf (M,T,I,S) حجم آزاد محاسبه شده از درصدهای حجمی از تکپار، بسپار(پلیمر، جسمى که از ترکيب ذرات متشابه الترکيب واز تکرار واحدهاى ساختمانى يکنواخت ايجاد شده باشد) و حلال در راکتور (برای وابستگی تابعی Vf به دمای T و غلظتها محاسبه شده تحت فرض اختلاط ایده آل) است.
برای هدف طراحی کنترل مناسبتر است که معادلات بالا را به صورت بدون بعد بنویسیم یعنی :
که و متغیرهای بی بعد به صورت زیر تعریف میشوند
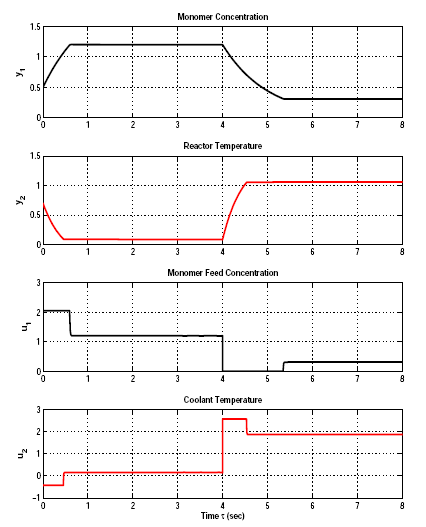
هدف کنترلی تنظیم غلظت تکپار y1=x1 و دمای راکتور y2=x2 بوسیله دستکاری غلظت تغذیه تکپار u1=x1f و دمای سرد کننده u2=x2c است.
ما اندازه گیری خروجی ها را با دسترسی روی خط (online) فرض می کنیم.غلظتهای اولیه و حلال به ترتیب x4 , x3 غیر قابل اندازه گیری فرض شده اند.بنابراین ورودیها مقید فرض شده اند به وسیله :
برای راحتی کار اینها را به کرانهای اشباع متقارن تبدیل کردیم ؛ با تعریف:
توجه کنید که سیستم درجه نسبی بردار خوش تعریف ρ={1,1} دارد و برای هر مقدار تعادل تعیین شده یک نقطه تعادل منحصر به فرد
و ورودی تعادل
در
دارد.
می توانیم (9) را دوباره در فرم (1) بنویسیم.
ماتریس A(.) به صورت ساده diag(1,β) است پس میتوانیم (4) به صورت همانند بگیریم.
سپس کنترل تجزیه شده و می توانیم به سادگی قرار دهیم:
که : وμ1 و μ2 ثابتهای مثبت به اندازه کافی کوچک هستند.
به منظور مقایسه نتایج با کنترلر Kurtz [2000] همان مقادیر عددی آنجا را برای پارا پارمترهای عددی دیگر عبارتند از:
احتمالا مقادیر x(0) نادرستند زیرا در منبع چهارم چیزی غیر از این آورده شده است.
در Kurtz [2000] نقاط تنظیم به صورت انتخاب شده بودند.
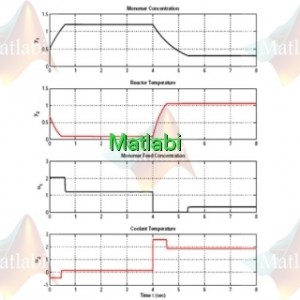
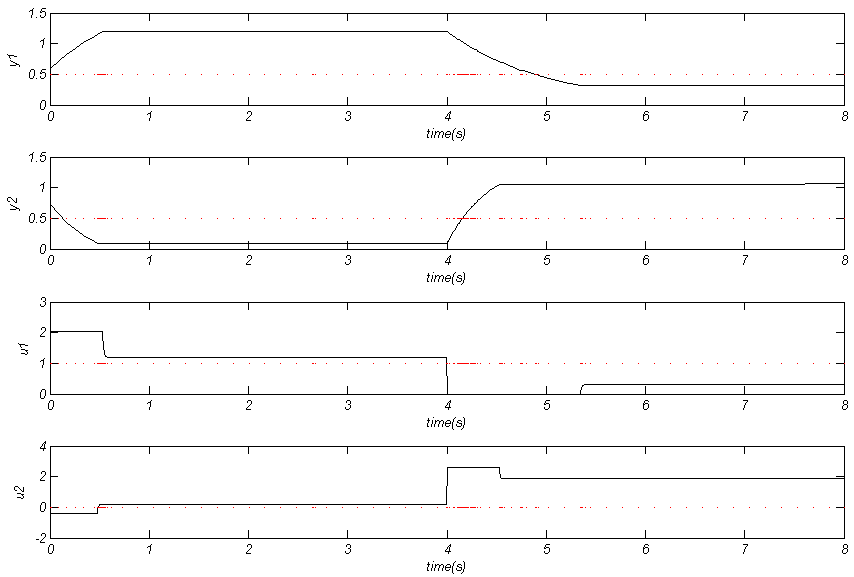
در زیر نقطه تنظیم به در τ =4s تغییر داده شده است.
(تغییر نقطه تعادل در ثانیه چهارم )نتایج در شکل بعدی نمایش داده شده است و واضح است که کنترلر با وجود این حقیقت که تقریبا هیچ کدام از مقادیر پارامترهای پلنت در طراحی کنترل صریحا استفاده نشده اند، عملکرد خوبی را بدست آورده است.
نتایج ما حداقل به خوبی کنترلر MPC ، Kurtz [2000] که طراحی خیلی بغرنج و پیچیده است، می باشد. (مقادیر عددی پارامترها در منبع چهارم آورده شده است)
مقاومت ذاتی این روش را برای عدم قطعیتهای پارامتری زمانیکه طراحی صریحا هیچ نیازی به اطلاعات این مقادیر پارامتری ندارد، یادآوری می کنیم.
مقاوم سازی برای اغتشاش با بکارگیری تکنیک مد لغزشی و کنترل انتگرالی تضمین شده است.
بالاخره طراحیهای کنترل ارائه شده به سادگی ، کنترلرهای PI/PID وفقی با ساختاری ضد انحلال هستند.
شکلهای بدست آمده از شبیه سازی با اجرای فایلهای
CSTR2a,CSTR2b,CSTR2c
نتیجه گیری:
در این مقاله ما دستاوردی برای تنظیم فیدبک خروجی راکتورهای شیمیایی همدما و گرمازا ارائه دادیم .
روش مذکور کاربردی از کار روی طراحی کنترل انتگرالی فیدبک خروجی مقاوم برای یک طبقه از سیستم های مینیمم فاز است.
برای درجه نسبی یک و دو سیستم ها کنترلر ما می تواند به سادگی بعنوان کنترلرهای PI/PID رایج صنعتی با خاصیت ضد انحلال طرح شده باشد.
این دستاورد مزایای مهمی را در برمیگیرد:
سادگی محاسباتی
توانایی دستکاری قیود
بکارگیری حالت جزئی و/یا فیدبک خروجی
کلید واژه : کنترل مقاوم، چند متغیره، کنترلر PI, MIMO
Process Control, Output Regulation, Integral Control, Sliding-mode Control,Output feedback
شبیه سازی مقاله Robust Multivariable PI Control
توسط کارشناسان سایت متلبی تهیه شده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

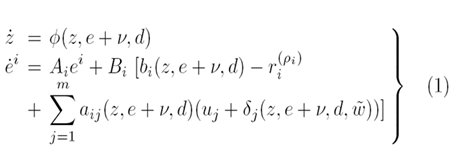
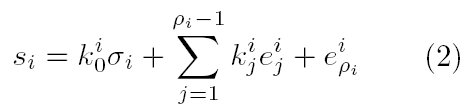
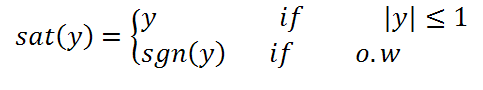
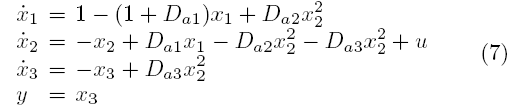
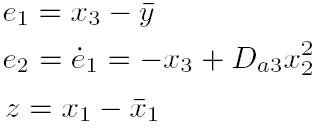
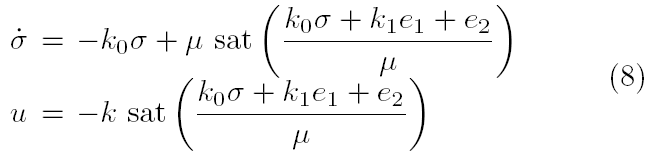
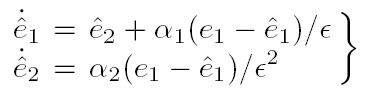
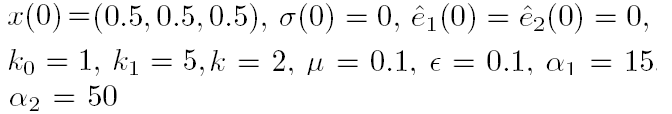
![پاسخ های گذرا حداقل در مقایسه با Scaratt , [2000]](https://www.matlabi.ir/wp-content/uploads/2017/10/siso1-bmp.png)
![پاسخ های گذرا حداقل در مقایسه با Scaratt , [2000]](https://www.matlabi.ir/wp-content/uploads/2017/10/word-image-942.png)
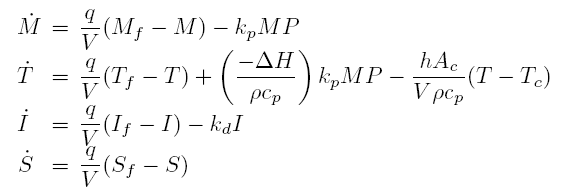
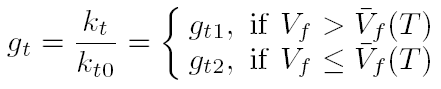
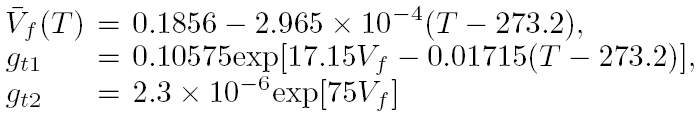
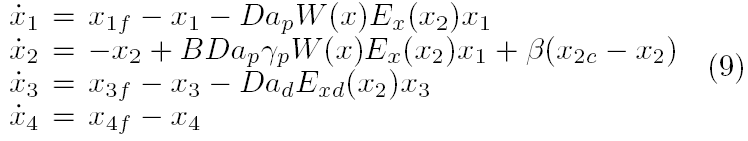
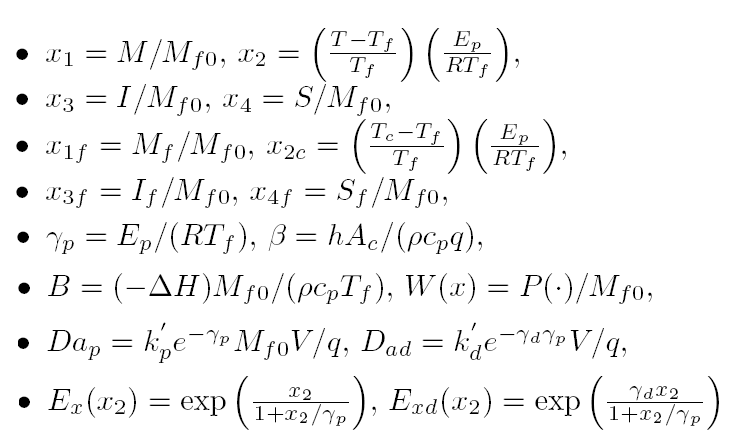
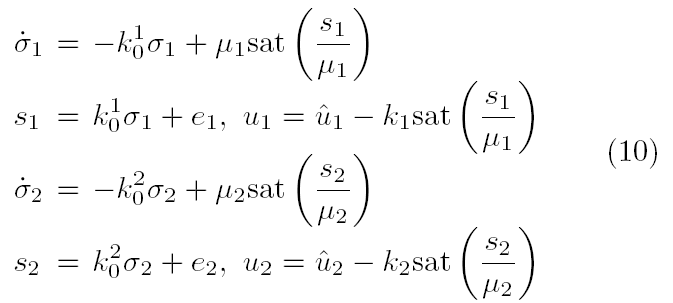



دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.