توضیحات
Robust inverse optimal control for discrete-time nonlinear system stabilization
کنترل بهینه معکوس مقاوم برای پایدارسازی سیستم غیرخطی زمان گسسته
چکیده
این تحقیق، بدون نیاز به حل معادله همبسته همیلتون-جاکوبی-بلمن (HJB)[1] کنترل بهینه معکوس برای پایدار سازی سیستم غیر خطی زمان گسسته را ، مورد بررسی قرار میدهد. در ادامه، این روش برای سیستم های غیرخطی زمان گسسته تحت اثر اغتشاش نیز راهکار ارایه میدهد و با ارایه دو مثال کارایی این روش ها را نشان میدهد. این روش ها با استفاده از یک تابع لیاپانوف زمان گسسته، یک تابعی هزینه را کمینه مینمایند [1].
کلمات کلیدی:
کنترل بهینه معکوس, پایدار سازی سیستم غیر خطی زمان گسسته, سیستم های غیرخطی زمان گسسته تحت اثر اغتشاش, معادلات همبسته همیلتون-جاکوبی-بلمن(HJB), تابع لیاپانوف
مقدمه
کنترل بهینه، غالبا به دنبال کمینه کردن یک تابعی هزینه میباشد، تابعی ای که معمولا تابعی از حالت ها و ورودی کنتزلی است. برای کنترل غیرخطی بهینه، مشکل اصلی، حل معادله HJB میباشد. تا به حال این معادله بطور عمومی برای سیستم های غیرخطی غیر قابل حل باقی مانده است. برای غلبه بر این مشکل، کنترل بهینه معکوس ارایه شده است [2,3]. برای دوری از اضافات از ذکر سایر جزییات پرهیز میکنیم.
کنترل بهینه معکوس که برای سیسیتم های غیر خطی کاربرد دارد، بر اساس تابع لیاپانوف میباشد [3,4,5]. وجود یک تابع لیاپانوف، پایداری را برآورده میسازد. اما تاکنون برای سیستم های غیر خطی، به طور عمومی روش مدونی ارایه نشده است. در این تحقیق، این تابع لیاپانوف با استفاده از روش بهنیه سازی ازدحام ذرات (PSO)[2] بدست آمده است [6].
محققان این تحقیق، یک روش کنترل بهینه معکوس برای سیستم های غیر خطی زمان گسسته ارایه کرده اند که فارغ از حل معادله همبسته HJB میباشد. همچنین این روش یک تابعی هزینه را کمینه میکند. علاوه بر این، برای نزدیکتر شدن به شرایط واقعی، سیستم شامل اغتشاش، پارامترهای نامعین و همچنین دینامیک های مدل نشده، در نظر گرفته شده است. هر کدام از این موارد میتواند کارایی کنترل کننده بر پایه مدل را تحت تاثیر قرار دهد. بدین منظور کنترل بهینه معکوس مقاوم برای مواجهه با سیستم های غیرخطی زمان گسسته تحت اثر اغتشاش ارایه شده است. همچنین این روش نیازی به حل معادله دیفرانسیل همبسته با مشتقات جزیی همیلتون-جاکوبی-ایساک (HJI)[3] ندارد[1].
بعلاوه با توجه به مزیت کار کردن با سیستم های زمان گسسته که از جمله آن، پیاده سازی مستقیم روی میکروپروسسور ها میباشد، این نوع مورد بررسی قرار گرفته است[1].
بخش دوم و سوم این گزارش، بترتیب دربرگیرنده قضایای یک و دو است که بترتیب برای پایداری و پایداری مقاوم میباشند، در قسمت چهارم نتایج شبیه سازی نشان داده شده است. قسمت آخر نیز شامل تحلیل خودم از این مقاله و کارهای مشابه میباشد.
پایدارسازی کنترل بهینه معکوس
سیستم غیر خطی زمان گسسته زیر را در نظر بگیرید
همچنین تابعی هزینه زیر را در نظر بگیرید
که در آن
قضیه 1:
سیستم (1) را در نظر بگیرید، اگر ماتریس P به گونه ای وجود داشته باشد که P=PT>0 باشد و در نامساوی زیر صدق کند:
که در آن
آنگاه با اعمال ورودی کنترلی زیر، نقطه تغادل xk=0 پایدار نمایی جامع خواهد بود.
علاوه بر این، (2) بعنوان یک تابعی هزینه کمینه میگردد.
پایدارسازی کنترل بهینه معکوس مقاوم
سیستم غیر خطی زمان گسسته زیر را در نظر بگیرید.
در این سیستم، جمله ی اغتشاش dk میتواند نماینده خطای مدل سازی، عدم قطعیت ها و یا اغتشاش باشد.
قضیه2:
سیستم غیر خطی زمان گسسته تحت اثر اغتشاش (9) را در نظر بگیرید، اگر ماتریس P به گونه ای وجود داشته باشد که P=PT>0 باشد و در نامساوی زیر صدق کند.
که در آن
همچنین:
که در این روابط و و توابع میباشند.
آنگاه با اعمال ورودی کنترلی زیر، تابعی هزینه (17) کمینه میگردد.
که در آن D مجموعه توابع کراندار محلی است که
که در آن یک تابع منفی معین است.[4]
شبیه سازی
مثال 1 (پایدارسازی) :
سیستم غیر خطی مرتبه 2 زمان گسسته زیر را در نظر بگیرید که به ازای ورودی صفر ناپایدار است. پارامترهای این سیستم بصورت زیر تعریف میشوند
مطابق (8) قانون کنترل بهینه پایدار ساز بصورت زیر است
که در آن
که ماتریس P آن با الگوریتم بهینه سازی PSO مطابق زیر بدست آمده است.
همچنین R=1 قرار میدهیم.
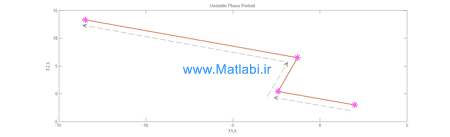
شکل 1 منحنی صفحه فاز سیستم حلقه باز(به ازای ورودی صفر) را به ازای شراطی اولیه x0=[2 -2]T نشان میدهد.
شکل 1
شکل 2 نیز تغییرات xk به ازای مقادیر اولیه x0=[2 -2]T تحت اثر قانون کنترلی پیشنهاد شده نشان میدهد. این شکل، شامل سیگنال کنترلی بهینه معکوس نیز میباشد.
شکل 2
همانطور که در شکل های بالا مشخص است، پایداری سیستم تامین شده است.
مثال 2 (پایدارسازی مقاوم):
قانون کنترل بهینه معکوس مقاوم در این تحقیق برای یک آونگ معکوس که بصورت قایم روی یک گاری قرار داده شده است، بکار گرفته شده است.
معادله دینامیکی زمان پیوسته این آونگ بصورت زیر تشان داده شده است.
در این معادله، متغیرهای حالت که شامل ,ω]ө[x,v, میباشند، بترتیب بیانگرموقعیت گاری، سرعت گاری، زاویه آونگ و سرعت زاویه ای هستند. M جرم گاری را مشخص میکند، m نمایانگر جرم نقطه ای متصل به انتهای آونگ است، l طول آونگ را مشخص میکند. g شتاب گرانش میباشد و نیز نمایانگر نیروی وارده است.
بعد از گسسته سازی توسط تقریب اویلر مدل بصورت زیر در میآید.
که در این معادلات T زمان نمونه برداری است که برابر 0.001 در نظر گرفته شده است.
علاوه بر این سیستم (22) تحت اثر اغتشاش [0,d2,k,0,d4,k]T قرار گرفته است که نتیجه آن در سیستم کلی به فرم زیر خواهد بود.
که در این معادله xk=[xk, vx,k, өk, ωk]T برابر خواهد بود.
ترم های اغتشاش نیز بصورت زیر در نظر گرفته میشوند.
در نهایت نیز قانون کنترل بهینه معکوس را به این سیستم تحت اثر اغتشاش اعمال میکنیم.
یعنی قرار میدهیم
همچنین M=3kg و m=1kg و l=0.5m و g=9.81 m/s2 قرار میدهیم.
مقادیر اولیه متغیرهای حالت را برابر=[0, -0.4, 0.5, 0]T [xk, vx,k, өk, ωk]T قرار میدهیم.
مقدار R=0.5 قرار داده و با استفاده از الگوریتم PSO مقدار ماتریس P را برابر زیر مقدار زیر قرار میدهیم.
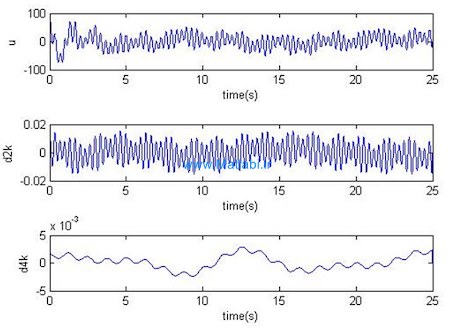
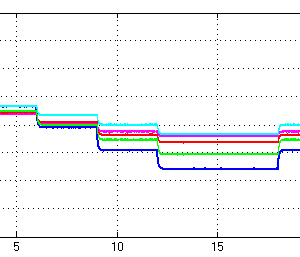
شکل 4 تغییرات متغیرهای حالت را با گذشت زمان نشان میدهد.
شکل 4
همانطور که مشاهده میکنید، پایداری مقاوم سیستم تامین شده است.
نمودار تصوریری ورودی کنترلی بهینه معکوس و همچنین اغتشاشات در شکل 5 به تصویر کشیده شده است.
شکل 5
- Hamilton-Jacobi-Belman ↑
- Particle Swarm Optimization ↑
- Hamilton-Jacobi-Isaacs ↑
- اثبات قضایای فوق در اصل مقاله آورده شده است ↑
در توضیحات بالا تمامی معادلات نیامده ولی در گزارش ورد همه آنها وجود دارند.
نتایج بدست آمده از شبیه سازی با متلب:


کلید واژه: کنترل بهینه معکوس، پایدار سازی سیستم غیر خطی زمان گسسته، سیستم های غیرخطی زمان گسسته تحت اثر اغتشاش، معادلات همبسته همیلتون-جاکوبی-بلمن(HJB)، تابع لیاپانوف
tabilization of discrete-time nonlinear, systems, Inverse optimal control, Discrete-time disturbed nonlinear systems, Control Lyapunov function, Hamilton–Jacobi–Bellman equation
شبیه سازی مقاله Robust inverse optimal control for discrete-time nonlinear system stabilization
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

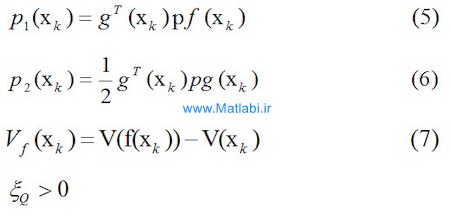
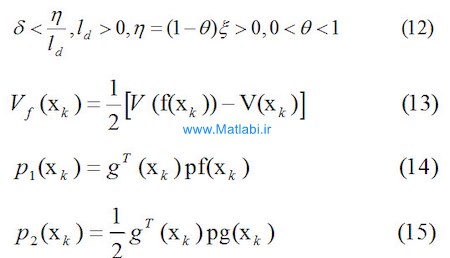

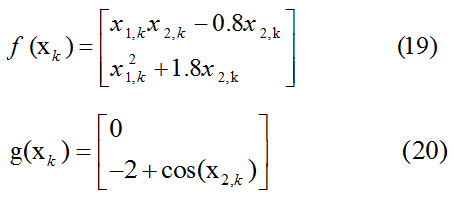
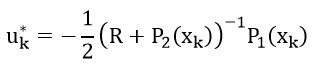
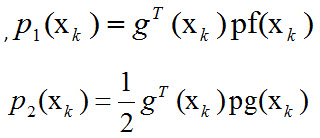







دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.