توضیحات
Robust Hinf Control of an Uncertain System Via a Stable Output Feedback Controller
ترجمه فارسی موضوع مقاله: کنترل Hinf مقاوم (رباست) توسط کنترلر فیدبک خروجی
فهرست شماره صفحه
1. مقدمه 1
2. بیان مسئله 1
3. فرآیند-S (S-Procedure) برای سیستمهای غیرخطی 7
4. قضیه کلیدی مورد استفاده برای استخراج نتایج اصلی 9
5. نتایج اصلی 17
6. مثال تمرینی 27
7. جمع بندی و نتیجه گیری 32
8. مراجع 34
در این نوشتار مسئله کنترل Hinf مقاوم (رباست) توسط کنترلر فیدبک خروجی مورد بررسی قرار میگیرد.
همان گونه که میدانید، در بسیاری از مسایل عملی کنترل استفاده از کنترل کنندههای پایدار نسبت به کنترل کنندههای ناپایدار، بسیار مطلوبتر است.
و این بدین دلیل است که، استفاده از کنترل کنندههای ناپایدار میتواند منجر به مشکلاتی مانند نقص در محرکها و سنسورها، حساسیت بالا نسبت به عدم قطعیتهای پروسه (پلنت یا Plant) و مشکلات پیاده سازی میگردد [1].
در این نوشتار فنی، روش جدیدی برای حل مسئله کنترل Hinf مقاوم از طریق کنترل کننده فیدبک خروجی و پایدار پیشنهاد داده خواهد شد.
برای این منظور دستهای از سیستمهای نایقینی که دارای عدم قطعیت ساختاری و توصیف شده با قیود مربعی انتگرالی (Integral Quadratic Constraints یا IQCs) میباشند، در نظر گرفته میشوند. نتایج ارایه شده بر مبنای نتایجی هستند که در [2] بیان شدهاند.
نتایج بدست آمده در، بیانگر شروط لازم و کافی برای پایدارسازی مطلق (Absolute Stabilization) اینچنین سیستم نایقینی (با عدم قطعیت ساختاری و شروط IQC) به همراه تضعیف اغتشاش تا سطحی معین، بدون لزوم پایداری کنترل کننده فیدبک خروجی، میباشند.
ایده اصلی برای روش ارایه شده در اینجا این است که ابتدا با سیستمی که در مرجع [2] در نظر گرفته شده است، شروع میکنیم و سپس یک عدم قطعیت اضافی تعریف کرده و اضافه مینماییم تا سیستم نایقینی جدیدی بدست آید.
این عدم قطعیت اضافی، دارای این ویژگی است که برای یک مقدار مشخص از عدم قطعیت، سیستم نایقینی جدید تبدیل به سیستم نایقینی اصلی می شود و بنابراین هر کنترل کننده مناسب برای سیستم نایقینی جدید، خواهد توانست مسئله پایدارسازی مطلق به همراه تضعیف اغتشاش تا سطحی معین را برای سیستم اصلی (اولیه) نیز حل نماید.
علاوه بر این، به ازای یک مقدار دیگر برای عدم قطعیت جدید، سیستم نایقینی جدید تبدیل به یک سیستم یقینی حلقه باز میگردد به نحوی که کنترل کننده بایستی پایدار شود.
چون در روش پیشنهادی ما، عدم قطعیتهای جدیدی اضافه میشود، بنابراین آنچه حاصل میشود شرایط کافی هستند تا شرایط لازم.
لذا در نهایت به شرایط کافی برای پایدار سازی مطلق با سطح معینی تضعیف اغتشاش خواهیم رسید.
با این حال، به دلیل اینکه عدم قطعیت جدید به صورت صریح ساخته شده است، لذا می تواند شاخصی برای میزان محافظهکاری در نظر گرفته شده باشد.
نتیجه اصلی ارایه شده در اینجا، از طریق اعمال روش ارایه شده در [2] به سیستم نایقینی جدید به دست آمده است.
با این کار، یک کنترل کننده فیدبک خروجی پایدار به دست خواهد آمد که مسئله پایدار سازی مطلق به همراه تضعیف اغتشاش تا سطحی معین را حل مینماید.
این امر از طریق حل یک جفت معادله ریکاتی وابسته به مجموعهای از پارامترهای مقیاسی (scaling parameters) محقق می شود و کنترل کننده طراحی شده نیز هم مرتبه با پلنت تحت بررسی خواهد بود.
در ادامه، مطالب به ترتیب زیر ارایه خواهند گشت:
در بخش(2) مسئله پایدار سازی مطلق به همراه تضعیف اغتشاش تا سطحی معین از طریق کنترلر فیدبک خروجی پایدار بیان میگردد.
در بخش (3) یک تعمیم از فرآیند-S (S-Procedure) [3] برای حالتی که سیستم غیرخط است ارایه میشود.
در بخش (4) شرایط لازم و کافی برای پایدارسازی مطلق با تضعیف اغتشاش نا سطح معینی بررسیرا بررسی مینماییم.
در بخش (5) سیستم نایقینی جدید که نتایج ارایه شده در بخش (4) ، به آن اعمال خواهد شد، معرفی میشود و برای آن کنترل کننده پایداری طراحی میشود که پایدارسازی مطلق به همراه تضعیف اغتشاش تا سطحی معین را تضمین کند.
برای تشکیل این سیستم نایقینی جدید بایستی فیدبک حالت، روش اشاره شده در بخش (4) را به سیستم نایقینی اصلی اعمال نمود.
این کار منجر به نتیجه اصلی این نوشتار یعنی ارایه روشی برای طراحی کنترل کننده مورد نیاز خواهد شد.
این روش شامل حل یک زوج معادله جبری ریکاتی از نوع Hinf که به مجموعهای از پارمترهای مقیاسی وابستهاند، میباشد و کنترا کننده نهایی از روی جوابهای معادله ریکاتی ساخته خواهند شد.
در بخش (6) برای بررسی و روشن شدن درستی تئوری ارایه شده، یک مثال ارایه میشود.
در این مثال مسئله کنترل Hinf برای یک سیستم خطی مستقل از زمان (LTI) بدون وجود عدم قطعیت، که از مرجع [4] برداشته شده است، حل خواهد شد و نشان داده میشود که برای این مثال، روش ارایه شده در اینجا نسبت به روش ارایه شده در مرجع [4]، کمتر محافظه کارانه است.
در بخش (5) نیز به بیان جمع بندی و نتیجه گیری میپردازیم.
در این بخش، مثال ارایه شده در مرجع [4] را برسسی مینماییم.
حل این مثال، درستی تئوری ارایه شده در بالا را نشان خواهد داد و نیز این امکان را ایجاد میکتد تا میزان محافظه کارانه بودن روش این نوشتار با روش ارایه شده در [4] مقایسه گردد.
توجه نمایید که در مرجع [4] فقط مسئله کنترل Hinf برای سیستمهای نایقینی با شرط IQC روی عدم قطعیتشان در نظر گرفته شده است.
در این مثال توجه خود را روی مسئله کنترل Hinf برای یک سیستم LTI بدون عدم قطعیت متمرکز مینماییم.
مثال مورد نظر، یک مسئله Mixed Sensitivity Hinf Control برای سیستمی با تابع تبدیل زیر میباشد.
تابع تبدیلهای وزنی نیز به صورت زیر تعریف میشوند.
…
مسئله کنترل Hinf بهینه موردنظر به صورت زیر است و باید ی را بیابیم که:
…
این مسئله Hinf منجر به سیستمی به فرم (2-1) میشود که توسط معادلات حالت زیر بیان میگردد.
…
در مرجع [4] نشان داده شده است که به ازای هر مقدار از پارامتر تضعیف اغتشاش که باشد، کنترل کننده Hinf استاندارد طراحی شده برای این سیستم، ناپایدار خواهد بود.
حال روش ارایه شده توسط این نوشتار که در قضیه(5-1) عنوان شده است را به کار میبندیم.
برای و داریم که شرایط قضیه(5-1) برقرار هستند و لذا میتوان کنترل کننده مربوطه (4-4) را تشکیل داد که،
…
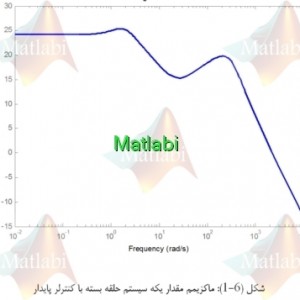
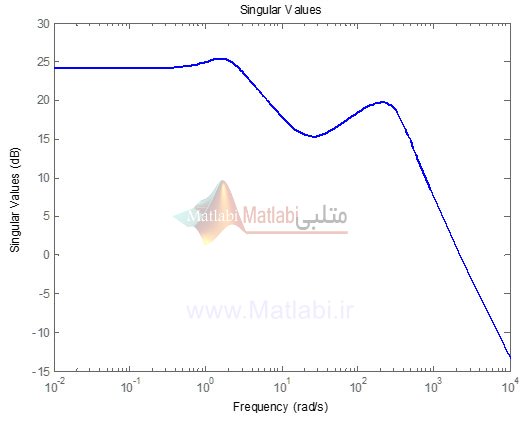
این کنترل کننده پایدار است که قطبهای آن در ، ، و قرار دارند.علاوه بر این وقتی که این کنترل کننده به سیستم (25) اعمال میشود، سیستم حلقه بسته را بدست آورده و ماکزیمم مقدار یکه آن را رسم مینماییم که شکل بدست آمده در شکل (6-1) و (6-2) رسم شده است.
شکل (6-1): ماکزیمم مقدار یکه سیستم حلقه بسته با کنترلر پایدار
شکل (6-2): ماکزیمم مقدار یکه سیستم حلقه بسته با کنترلر پایدار
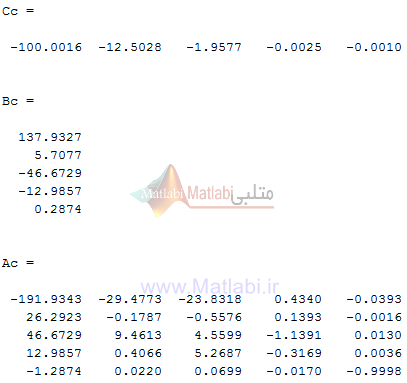
برنامه نوشته شده در متلب را اجرا کرده و نتایج زیر به دست آمده است.
شکل (6-3): جواب جفت معادله ریکاتی
شکل (6-4): ماتریسهای مربوط به کنترل کننده نهایی
شکل (6-5): مقادیر ویژه مربوط به کنترل کننده نهایی که پایدار است
شکل (6-6): مقادیر ویژه مربوط به سیستم حلقه بسته نهایی که پایدار است
میتوان ملاحظه کرد که، این کنترل کننده پایدار، مسئله پایدار سازی قوی Hinf را که تحت بررسی بود، حل نموده است و ماکزیمم مقدار یکه سیستم حلقه بسته 32dB را بدست آورده است.
این مقدار مربوط به نرم Hinf حلقه بسته برابر 40.11 است که در مقایسه با نرم Hinf برابر 42.51 بدست آمده از روش مرجع [4]، نشان دهنده کمتر محافظه کارانه بودن روش ارایه شده در این نوشتار [قضیه(5-1)] میباشد.
در این نوشتار، روش جدیدی برای مسئله پایدارسازی با سطح معینی از تضعیف اغتشاش بوسیله یک کنترل فیدبک خروجی پایدار ارایه شد.
نکته اصلی این روش نیز اضافه کردن یک پارامتر نایقینی به سیستم اصلی بود.
برای مقداری از این نایقینی اضافه شده، سیستم نایقینی جدید تبدیل به سیستم اصلی میشود و برای مقدار دیگری از پارامتر نایقینی اضافی، سیستم تبدیل به سیستمی میشود که ورودی کنترلی تاثیری روی سیستم ندارد و کنترلر در حلقه باز قرار میگیرد که همین موجب پایدار گشتن کنترلر میشود.
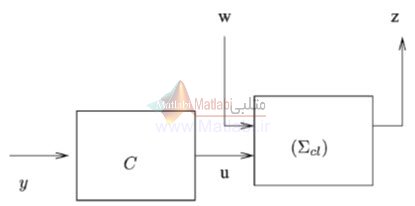
پایه روش ارایه شده در اینجا، استفاده از یک کنترل کننده فیدبک حالت برای تعریف یک سیستم نایقینی جدید است که برای مقدار معینی از عدم قطعیت اضافه شده، منجر به وضعیت حلقه باز نشان داده شده در شکل (5-1) میگردد.
با این حال، به طور معادل میتوان روشی دوگان را اعمال کرد و در آن از تزریق خروجی (output injection) استفاده نمود که منجر به وضعیت حلقه باز نشان داده شده در شکل (7-1) میگردد.
شکل (7-1): دیاگرام حلقه باز که از اعمال روش تزریق خروجی بدست میآید
در عمل میتوان هر دو روش را به کار بست و روشی را که تضعیف اغتشاش کمتری میدهد، را برگزید.
ایده اصلی و راهگشا در این نوشتار فنی، تعریف یک عدم قطعیت جدید است.
این روش ذاتا مقداری محافظه کارانه است.
با این حال، عدم قطعیت جدید، یک پارامتر نایقینی ثابت و نامعلوم میباشد و بنابراین محافظه کاری موجود در روش ارایه شده را میتوان با تعریف ضرایبی مانند ضرایب نوع Popov [11] و یا ضرایب دینامیکی نوع Zames-Falb [12] به منظور بدست آوردن ساختار این عدم قطعیت اضافه شده، کاهش داد.
استفاده از ضرایب دینامیکی موجب سنتز کنترلری خواهد شد که مرتبهاش از مرتبه پلنت بالاتر است.
علاوه بر این میتوان از ابزارهای بهینه سازی مانند ژنتیک الگوریتم و یا روش PSO (Particle Swarm Optimization) استفاده کرد و پارامتر مناسبی را از طریق این ابزار بدست آورد.
این پارامتر هم می تواند تابع هزینه و هم پارمترهایی مثل ها و یا باشد که میتوناد مبنایی برای کارهای بعدی باشد.
جهت تهیه فایل شبیه سازی با متلب و گزارش کامل باید این محصول خریداری شود.
کلید واژه : کنترل مقاوم
Partial state feedback, Sliding mode control, Ball and beam system
شبیه سازی مقاله Robust Hinf Control of an Uncertain System Via a Stable Output Feedback Controller
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.



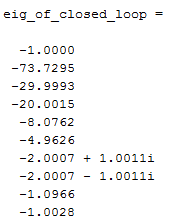



دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.