توضیحات
Advanced Textbooks in Control and Signal Processing
Robust Control of a Distillation Column
شبیه سازی در متلب 2006 انجام شده و با ورژن های جدید متلب سازگار نیست.
ترجمه فارسی موضوع مقاله: کتاب های درسی پیشرفته در کنترل و پردازش سیگنال- کنترل مقاوم یک ستون تقطیر
توجه برخی از بخش های گزارش در توضیحات این صفحه عمدا حذف شده است. با خریداری این محصول میتوانید نسخه کامل آن را داشته باشید.
مقدمه
تقطير، در واقع ، جداسازي فيزيکي برشهاي نفتي است که اساس آن، اختلاف در نقطه جوش هيدروکربنهاي مختلف است. هر چه هيدروکربن سنگينتر باشد، نقطه جوش آن زياد است و هر چه هيدروکربن سبکتر باشد، زودتر خارج ميشود. اولين پالايشگاه تاسيس شده در جهان ، در سال 1860 در ايالت پنسيلوانياي آمريکا بوده است. نفت خام ، از کورههاي مبدل حرارتي عبور کرده، بعد از گرم شدن وارد برجهاي تقطير شده و تحت فشار و دما به دو صورت از برجها خارج ميشود و محصولات بدست آمده خالص نيستند.
در اين بخش هدف اين است که ابتدا با عمليات فيزيکي که در برج تقطير انجام مي شود، آشنايي صورت مي گيرد سپس اجزايي که در ستون تقطير استفاده مي شوند و براي فهم ديناميک آن لازم هستند، معرفي مي شوند.
تعريف تقطير :
فرايندي که در آن مخلوط[1] مايع يا بخار از دو يا چند ماده، به بخش هايي از اجزا ترکيبي[2] آن با خلوص مطلوب، با بکارگيري و حذف گرما، تفکيک مي شود.
بناي تقطير بر اين حقيقت استوار است که بخار يک مايع در حال جوش [3] در جز ترکيبي که نقطه جوش پايينتري دارد، غنيتر است.
لذا زماني که اين بخار سرد شده و بصورت مايع درآيد، مايع حاصل شامل جزترکيبي فرارتر[4] خواهد بود و در عين حال، مخلوط اصلي شامل مقدار بيشتري از ماده کمتر فرار است.
هدف از طراحي برج تقطير اين بوده است که چنين جداسازي با کارامدي بيشتري صورت گيرد.
سه جنبه مهم از نقطه نظر ساخت وتوليد[5] مربوط به فرايند تقطير عبارتند از :
- معمولترين فرايند جداسازي، تقطير است.
- بدليل نيازمندي هاي گرمادهي[6] و خنک کاري [7] ، اين فرايند مصرف انرژي بالايي دارد.
- فرايند تقطير بيش از 50% هزينه هاي عملياتي[8] پلانت را به خود اختصاص مي دهد.
بنابراين بهترين روش جهت کاهش هزينه هاي عملياتي واحدهاي موجود اين است که کارايي و کارامدي اين فرايند را با استفاده از کنترل و بهينه سازي فرايند بهبود بخشيد. در دست يافتن به اين بهبود، درک اصول و مباني تقطير و چگونگي طراحي سيستم هاي تقطير اساسي است.
انواع زيادي از برج هاي تقطير وجود دارند که هر کدام جهت انجام نوع خاصي از جداسازي طراحي شده اند و هر طراحي از نظر پيچيدگي نيز از طراحي هاي ديگر متفاوت است.
يکي از شيوه هاي دسته بندي ستون تقطير اين است که آنها چگونه عمل مي کنند. بر اين اساس دو نوع برج وجود دارد :
- برج گسسته[9] : در اين نوع برج خوراک[10] بصورت گسسته به برج اعمال مي شود. يعني ابتدا برج با يک مقدار از خوراک تغذيه شده سپس فرايند تقطير انجام مي شود زمانيکه به هدف مورد نظر دست يافته شد، دسته ديگري از خوراک وارد برج مي شود.
- برج پيوسته[11] : بر خلاف برج گسسته، برج پيوسته يک جريان خوراک پيوسته را پردازش مي کند. هيچ وقفه اي تا زمانيکه مشکلي در برج يا در محيط اطراف وجود نداشته باشد، در جريان خوراک ايجاد نمي شود. برج پيوسته توان عملياتي[12] بالاتري داشته و نسبت به برج گسسته معمولتر هستند.
برج هاي تقطير را مي توان بر اساس ويژگي هاي ديگر بازهم تقسيم بندي کرد.
مثلاً بر اساس طبيعت خوراکي که پردازش مي شود دو نوع برج تقطير وجود دارد :
- باينري[13] : برجي که خوراک آن فقط شامل دو جزء است.
- چند جزئي[14] : برجي که خوراک ستون آن بيش از دو جزء ترکيبي دارد.
يا بر اساس جاييکه خوراک اضافي خارج مي شود بمنظور کمک به فرايند جداسازي، دو نوع برج وجود دارد که عبارتند از :
- تقطير استخراجي[15] : برجي که خوراک اضافي در جريان محصول پايين ظاهر مي شود.
- تقطير آزئتروپيک[16] : برجي که خوراک اضافي در جريان محصول بالا ظاهر مي شود.
و تقسيم بندي هايي از اين دست که بر حسب موارد ديگر انجام مي شود.
- مولفه هاي اصلي برج تقطير
برج تقطير از چندين مولفه تشکيل شده است که هر کدام يا جهت انتقال انرژي گرمايي استفاده مي شوند يا جهت ايجاد بهبود در انتقال مواد. يک تقطير نوعي شامل چندين مولفه اصلي است :
- يک قفسه عمودي[17] که عمل جداسازي اجزاء ترکيبي مايع، در آنجا انجام مي شود.
- المان هاي داخل ستون[18] نظير سيني ها[19] که براي بهبود بخشيدن عمل جداسازي مولفه ها استفاده مي شوند.
- گرم کننده[20] يا بويلر که باعث مي شود بخار لازم براي انجام فرايند تقطير فراهم شود.
- چگالنده[21] جهت سرد و متراکم کردن بخاري که از بالاي برج خارج مي شود.
- مخزن جريان برگشتي[22] (ريفلاکس) جهت اينکه بخار مايع شده اي که از قسمت بالاي برج مي آيد در اين مخزن نگهداشته شود و مايع بتواند به برج مجدداً بازگردد.
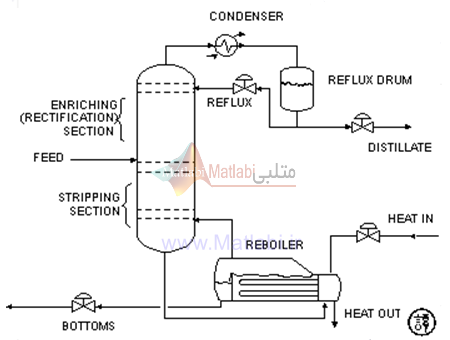
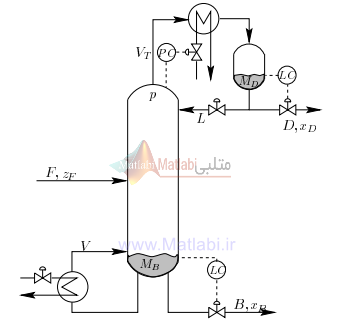
قفسه عمودي المان هاي داخلي برج را در خود جاي مي دهد و بهمراه چگالنده و بويلر يک برج تقطير را شکل مي دهند. شماتيکي از يک برج نوعي تک خوراک با دو جريان محصول، در شکل (1) نشان داده شده است.
شکل (1)
- عمليات هاي بنيادي
همانطور که پيشتر عنوان شد مخلوط مايعي که پردازش مي شود بعنوان خوراک شناخته مي شود و معمولاً در مکاني نزديک به وسط برج، وارد برج مي شود و به سيني که در آنجا قرار دارد اصطلاحاً سيني خوراک[23] اطلاق مي گردد.
سيني خوراک برج را به دو بخش بالايي[24] و بخش پاييني[25] تقسيم مي کند.
به بخش بالايي نيز بخش اصلاح[26] يا غني سازي[27] گفته مي شود. به بخش پاييني، بخش سلب[28] نيز گفته مي شود.
روند کار به اين صورت است که گرما براي توليد بخار به بويلر وارد مي شود.
اين گرما معمولاً توسط بخار ايجاد مي شود اما مي تواند خروجي ديگر ستون ها هم باشد. بخاري که از گرماي بويلر ايجاد شده در برج بالا رفته و سرانجام بصورت مايع به بويلر بر مي گردد.
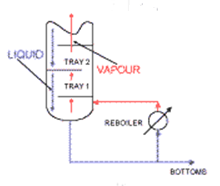
به مايعي که از بويلر به خارج از برج انتقال داده مي شود و بعنوان خروجي در نظر گرفته مي شود، محصول پاييني[29] گفته مي شود (شکل (2)).
شکل (2)
بخار حاصل از گرماي بويلر به بالاي برج حرکت مي کند و هنگاميکه از بالاي آن خارج مي شود بوسيله چگالنده، سرد مي شود.
مايع حاصل شده در مخزن ريفلاکس ذخيره مي شود.
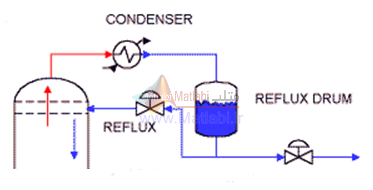
بخشي از اين مايع مجدداً به بالاي برج بازمي گردد که به آن ريفلاکس گفته مي شود و بخشي هم از واحد خارج مي شود که به آن محصول بالا[30] يا عصاره[31] گفته مي شود(شکل (3)).
بنابراين جريان هاي داخلي مايع و بخار درون برج وجود دارند به همان صورت که جريان هاي خارجي خوراک و محصولات به سمت داخل و خارج برج وجود دارند.
شکل (3)
در شکل (4) يک برج تقطير دو محصولي با نمادگذاري لازم جهت بدست آوردن معادلات حاکم بر رفتار سيستم، نشان داده شده است.
شکل (4)
مدل ديناميك ستون تقطير
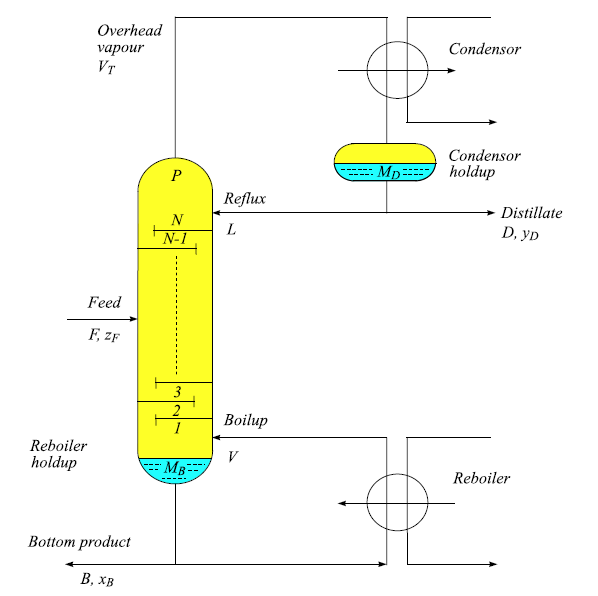
يک برج تقطير دو محصوله در شکل 5b نشان داده شده است.
هدف برج تقطير، جداسازي خوراک (F)، که ترکيبي از اجزا سبک و سنگين با ترکيب (Zf) است، به محصولات مقطر شده (D) با ترکيب (Yd)، که بيشتر شامل اجزا سبک است، و محصولات انتهايي برج (B) با ترکيب (Zb)، که شامل محصولات سنگين است.
براي نيل به اين هدف، برج تقطير حاوي يک سري از طبقهايي است که در سرتاسر ارتفاع آن چيده شدهاند.
مايع در داخل برج در ميان طبقها از بالا به پايين جريان پيدا ميکند، اين در حالي است که بخار از انتهاي برج به سمت بالا بلند ميشود.
ارتباط دايمي بين مايع و بخار منجر به افزايش غلظت اجزاي فرار در بخار ميشود، اين در حالي است که همزمان غلظت مواد با فراريت کم هم در مايع زياد مي گردد.
بهرهبرداري از برج نيازمند جوشش مجدد مقاديري از محصولات انتهاي برج با سرعت (V) براي اطمينان از پيوسته بودن جريان بخار و مقداري از مواد روان تقطير شده در طبق بالا با سرعت (L) براي اطمينان از پيوسته بودن جريان مايع ميباشد.
شکل 5b : سيستم برج تقطير
دعوت به همکاری برنامه نویسی با متلب
: نرخ جريان[32] خوراک (kmol/min)
: ترکيب خوراک (بصورت کسر مولي[33])
و : نرخ جريان محصول بالا و پايين (kmol/min)
و : ترکيب محصول بالا و پايين (معمولاً از ماده سبک) (کسر مولي)
: نرخ جريان ريفلاکس (kmol/min)
: نرخ جريان بويلاپ[34](kmol/min)
: تعداد طبقه هاي نظري[35] شامل گرم کننده
: تعداد کل طبقه ها شامل چگالنده کلي[36]
: شماره طبقه (1 نشان دهنده کف(پايين)[37] برج است و بيانگر طبقه خوراک )
و : نرخ جريان مايع و بخار از طبقه
و : ترکيب يا غلظت مايع و بخار در طبقه (معمولاً از ماده سبک) (کسر مولي)
: مقدار مايع نگهداشته شده[38] در طبقه (kmol) (: مايع نگهداشته شده در گرم کننده- : مايع نگهداشته شده در مخزن چگالنده)
: کل مايع نگهداشته شده در درون برج (kmol)
: فراريت نسبي[39] بين ماده سبک و سنگين
: ثابت زماني ديناميک جريان مايع در هر طبقه (min)
: تاخير زماني بين تغيير در ريفلاکس و رسيدن آن به گرم کننده (min)
: ثابت اثر جريان بخار روي جريان مايع
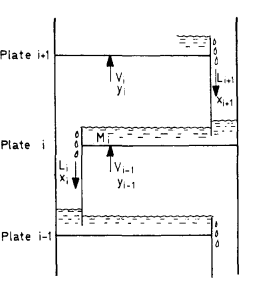
در شکل (4) طبقات برج نشان داده نشدند اما شکل (5) طبقات برج و نحوه نماد گذاري آنها را به وضوح نمايش مي دهد.
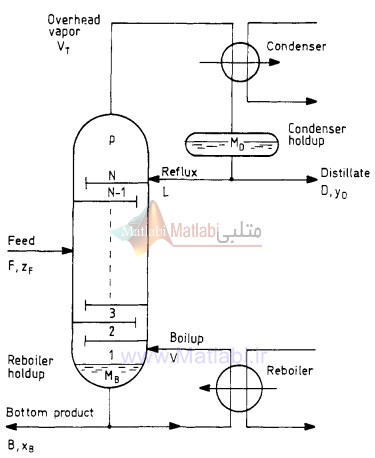
شکل (5)
نشانهگذاريهاي بهکار رفته در استنتاج مدل برج تقطير بهطور خلاصه در جدول 1-1 خلاصه شدهاند و برج اطلاعات آنها در جدول 2-1 داده شده است.
جدول 2-1 اطلاعات برج تقطير
انديس i شمارهي هر مرحله از انتهاي برج (i=1) تا بالاي آن (i=N) نشان ميدهد.
انديس B محصولات انتهايي و D محصولات مقطر شده را نشان ميدهد.
يک برج تقطير ويژه با خلوص بالا را ميتوان با 40 مرحله (39 طبق و يک ريبويلر) بهعلاوهي يک کندانسور در نظر گرفت.
بررسي مدل سيستم بدون کنترلکننده
بدست آوردن مقادير ويژه يا قطبهاي انتقال يک سيستم ميتواند ديد نسبتاً خوبي در مورد رفتار آن به ما بدهد.
بنابراين ميتوان قطبها و صفرهاي انتقال را به صورت زير مرتب نمود. قطبها همان مقادير ويژة ماتريس حالت سيستم ميباشند.
مشاهده ميکنيم که قطبها و صفر انتقال سيستم همگي در سمت چپ محور موهومي قرار دارند، لذا انتظار داريم که پاسخ سيستم به ورودي پلة واحد، پايدار و غيرمينيمم فاز باشد.
شبيهسازي پاسخ زماني سيستم
در نرمافزارMatlab پاسخپله واحد سيستم به صورت شکل(12) خواهد شد.
شکل(12)- پاسخ پله واحدحلقه باز سيستم بدون کنترلکننده
شبيهسازي پاسخ فرکانسي سيستم
پاسخ فرکانسي حلقة باز سيستمدر شکل(13) آمده است.
شکل(13)- نمودار بد حلقه باز سيستم بدون کنترلکننده
همانطور که در پاسخ زماني نيز مشاهده شد، اندرکنش بين کانالهاي سيستم قابل ملاحظه است که اين موضوع با دامنة نمودار بهرة بودي نيز مطابقت دارد.
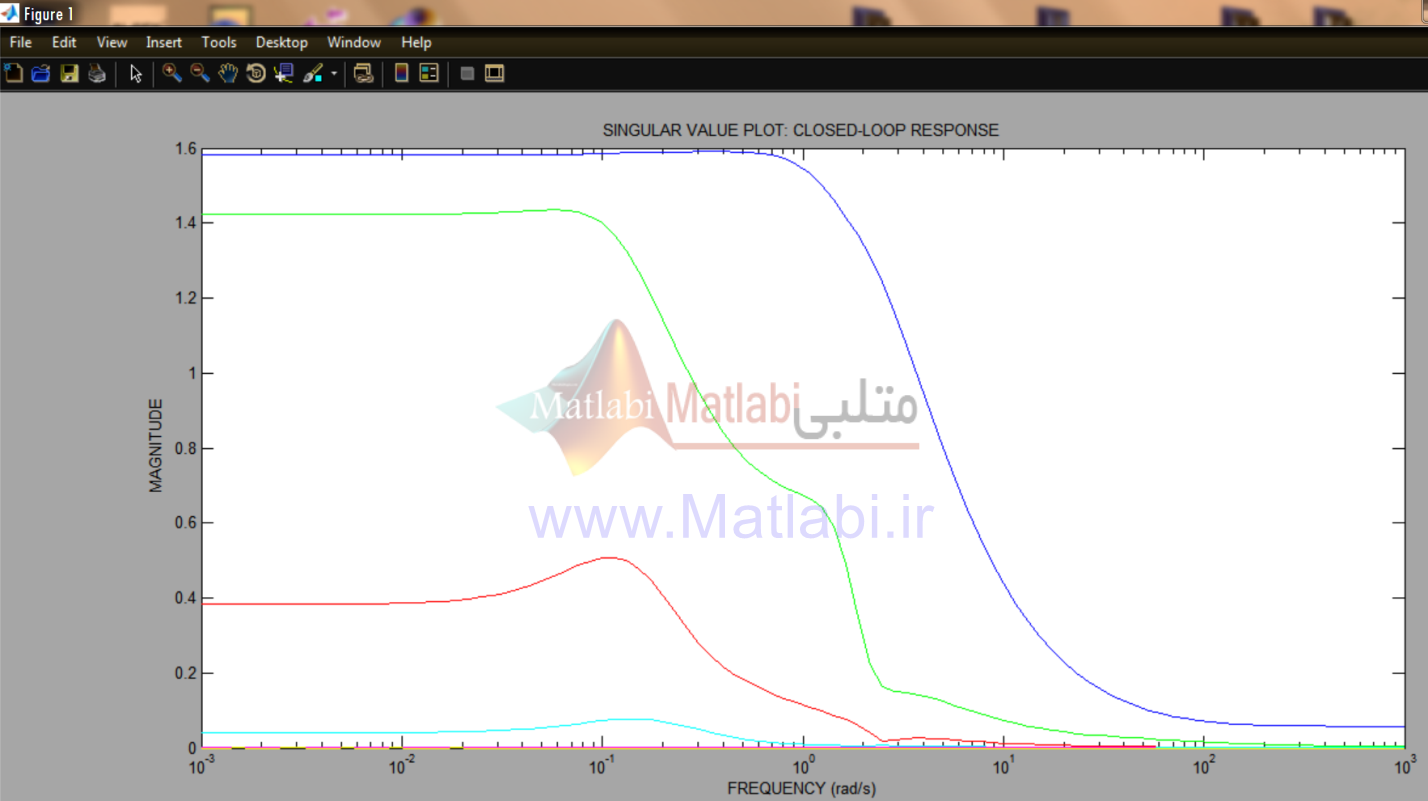
شکل 2-1: مقادير تكين G و G4
تمام دستورات لازم براي پيدا کردن مدل خطي مرتبهي 6 برج تقطير در فايل متلب mod_col.m گنجانده شده است.
پاسخ فرکانسي مقادير منفرد G با مدل مقادير منفرد مدل مرتبهي 82 خطيسازي شده G4 در شکل 2-1 مقايسع شده است. مشاهده مي شود رفتار هر دو مدل تا قبل از فرکانس 2 راديان بر دقيقه نزديک است.
كنترلر µ :
تکرار اول:
مسئله بهينه سازي براي کمينه کردن باند بالاي مقادير ميو و در نتيجه کمينه کردن ماکزيمم مقدار آن انجام مي شود.
سنتز ميو يافتن کمترين مقدار تابع هزينه و ساختن يک کنترل کننده K است که کارايي دلخواه را نزديک به سطح بهينه برآورد کند.
بعبارت ديگر هدف از سنتز ميو يافتن کنترل کننده پايدار کننده K است بطوريکه براي هر فرکانسي مقادير تکين ساخت يافته شرط زير را برآورده کند.
در واقع مي خواهيم که بيشترين مقدار تکين ساختاريافته سيستم تعميم يافتهM را کمتر از يک کنيم.
سنتز ميو توسط دستور dkit (که بيان کننده تکرار D-K است – مخفف D-K iteration) که از دستورات مربوط به جعبه ابزار کنترل مقاوم Matlab است و با تکرار D-K رويه حل مساله را اتوماتيک مي کند انجام مي گيرد.
قبل از اينکه از دستور dkit استفاده شود لازم است اختصاص متغيرهاي ضروري صورت گيرد که اين کار در برنامه dk_col صورت گرفته است.
پارامترهاي تعريف شده براي دستور dkit در برنامه dk_col عبارت است از:
NOMINAL_DK :متغيري است که شامل سيستم حلقه باز نامي است(سيستم تعريف شده در برنامه sys_ic گنجانده شده است)
NMEAS_DK :تعداد اندازه گيري ها( در واقع تعداد ورودي هاي کنترل کننده K است)
NCONT_DK :تعداد ورودي براي کنترل سيستم (تعداد خروجي کنترل کننده K)
BLK_DK :ساختار بلوک براي محاسبه ميو(شامل بلوک عدم قطعيت بعلاوه بلوک مربوط به عملکرد)
OMEGA_DK :تعداد اندازه گيري ها( در واقع تعداد ورودي هاي کنترل کننده K)
( دستور dkit در برنامه ms_col فراخواني مي شود )
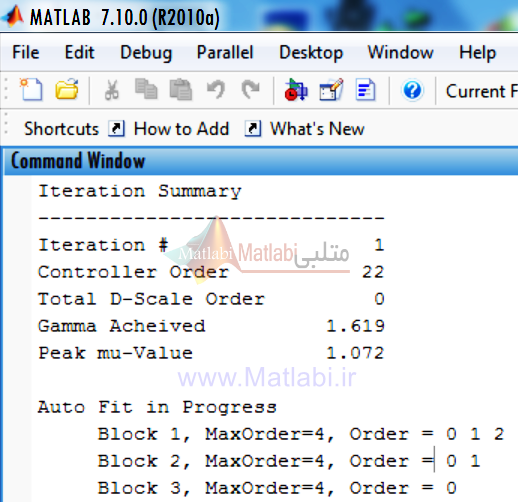
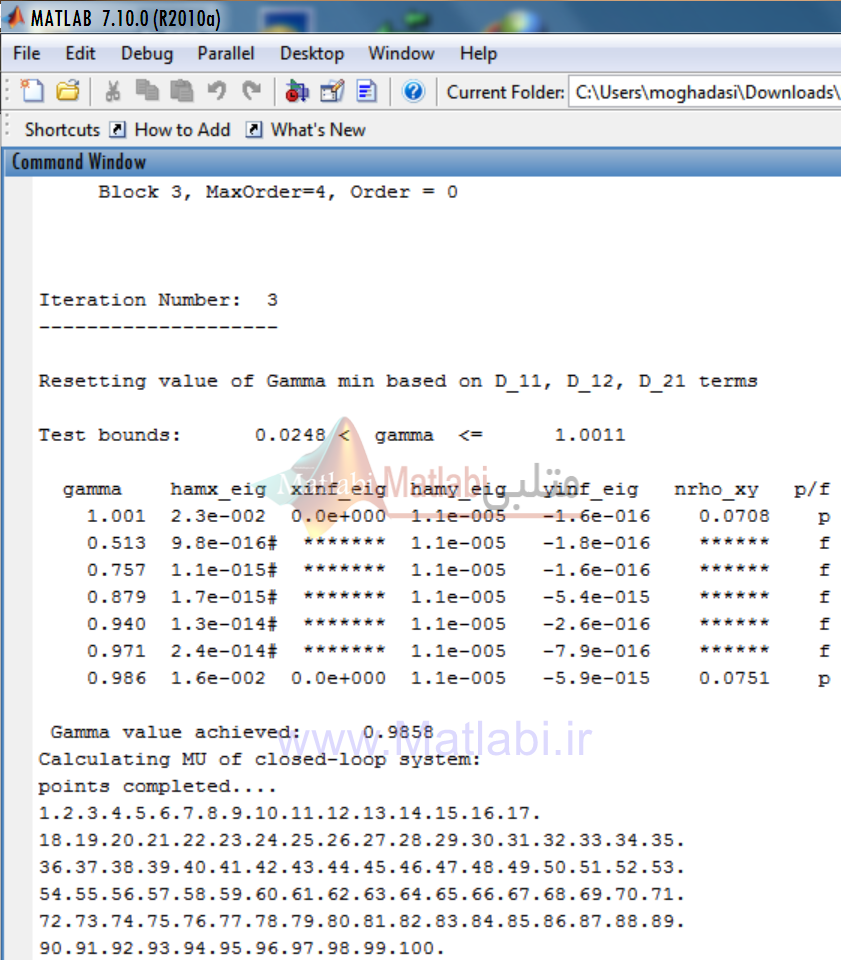
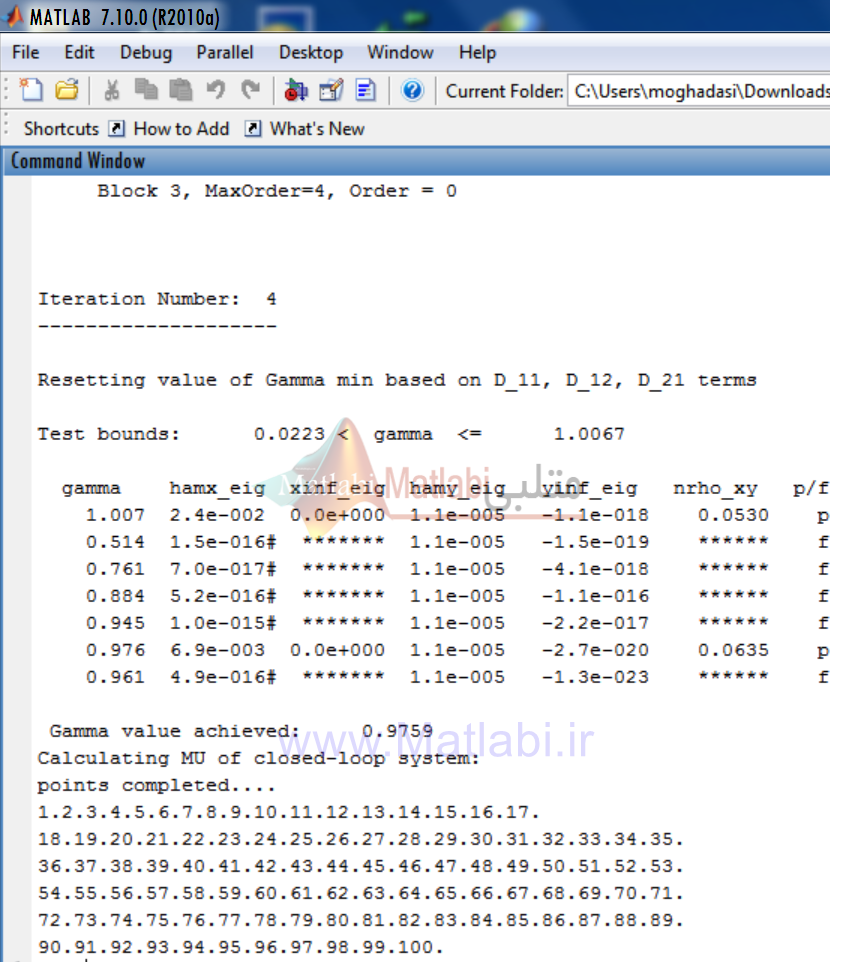
مشاهده مي شود که بيشترين مقدار ميو در اين مرحله 1.072 بدست آمده است و همچنين مرتبه مربوط به بلوک هاي قطري d هاي تشکيل دهنده D بيان شده است.
و بهمين ترتيب مراحل بعدي انجام شده تا در نهايت مقدارγ کمتر از 1 شود.
تکرار دوم :
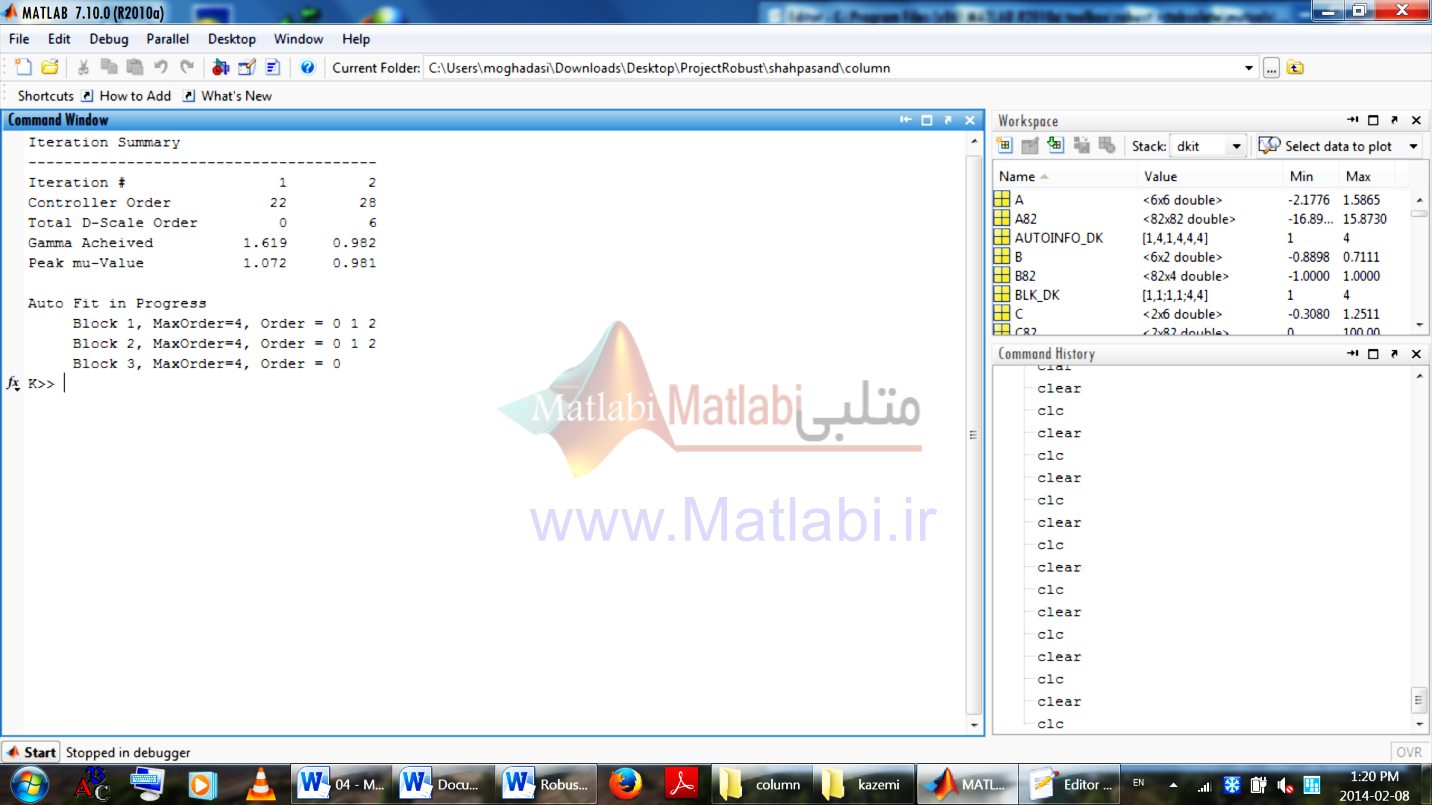
تکرار سوم :
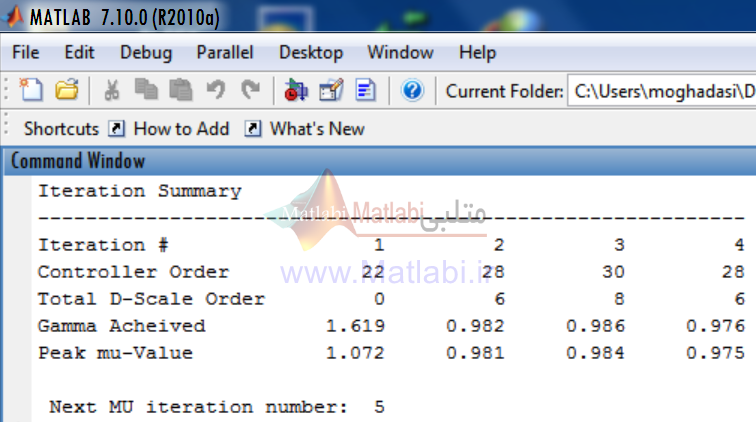
تکرار چهارم :
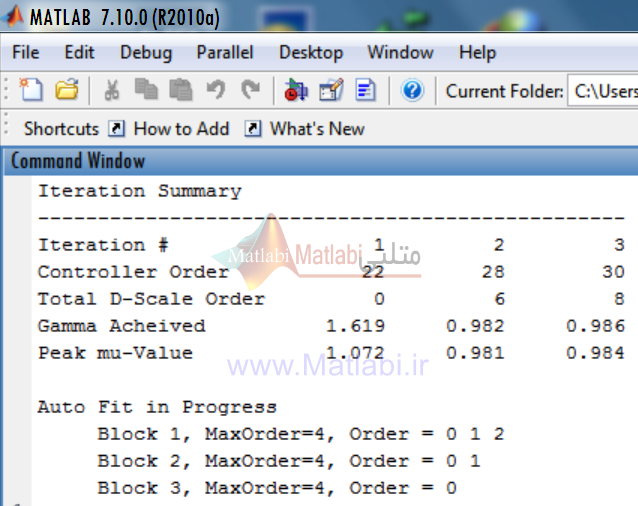
| تکرار | مرتبه کنترلر | ماکزيمم مقدار |
| 1 | 22 | 091/1 |
| 2 | 28 | 991/0 |
| 3 | 28 | 978/0 |
کنترل کننده حاصل از سنتز ميو در اينجا از مرتبه 28 و پس از 3 تکرار بدست آمده است.
در تکرار مقدار μ به 0.975 رسيده که بمعني داشتن عملکرد مقاوم با کنترل کننده طراحي شده است، چرا که مقدار تکين ساخت يافته در اينجا مقداري کمتر از 1 دارد.
مقدار گاما نيز بيان کننده مقداري است که نرم بي نهايت تابع از اين مقدار کمتر شده است و در واقع مساله زيربهينه بودندر اينجا مطرح است.
در اينجا کنترل کننده طراحي شده با سنتز ميو،K_muنامگذاري شده که بعد از چهار تکرار بدست آمده است.
کاهش مرتبه کنترلر حاصل با برنامه red_col انجام شده است. اختلاف بين دو تابع تبديل در شکل زير نمايش داده شده است.
بيشترين اختلاف عبارت است از:
کنترلر کاهش مرتبه يافته در Kred_g ذخيره شده است.
تحليل پايداري مقاوم، عملکرد نامي و مقاوم با برنامه mu_col :
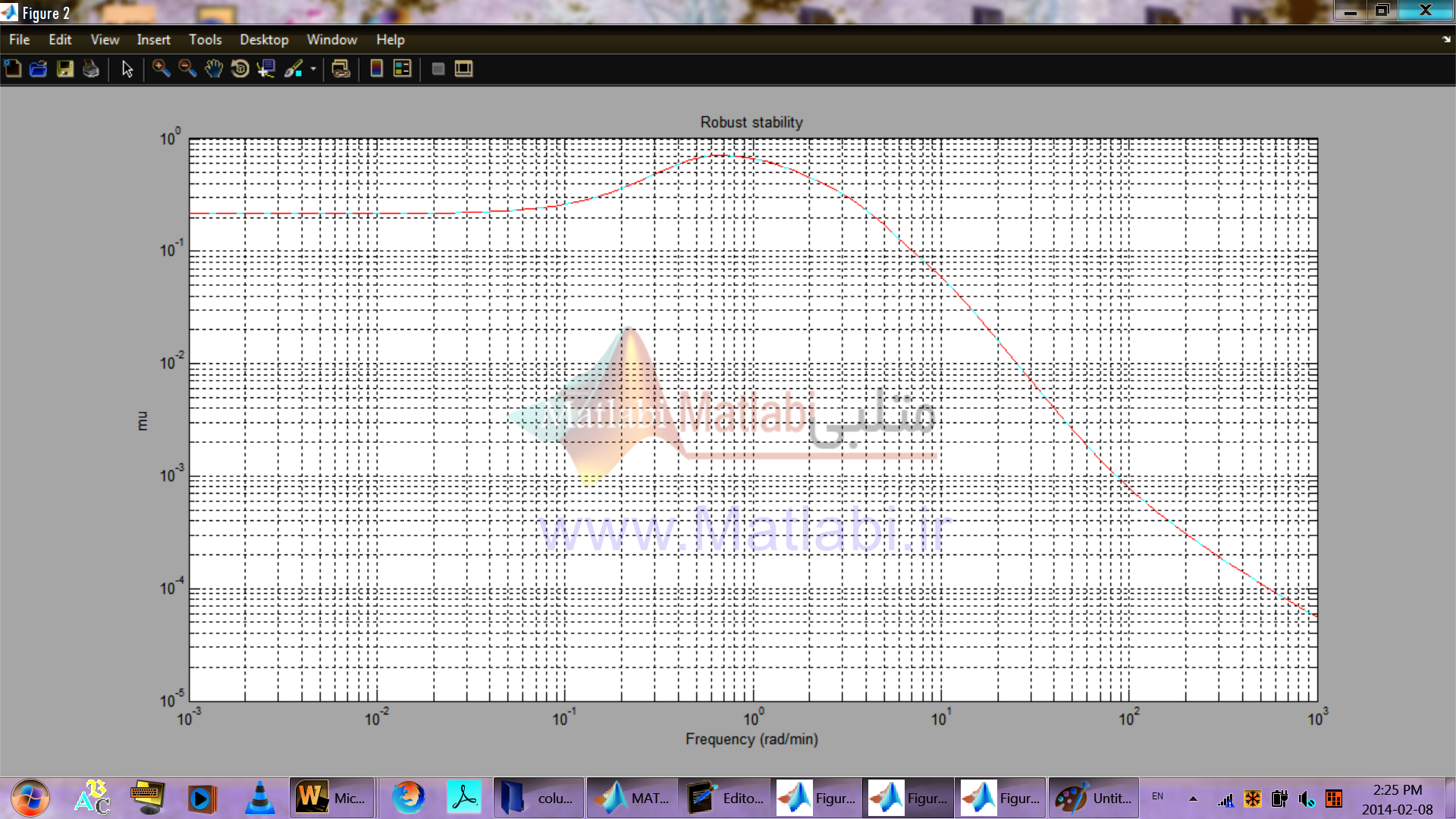
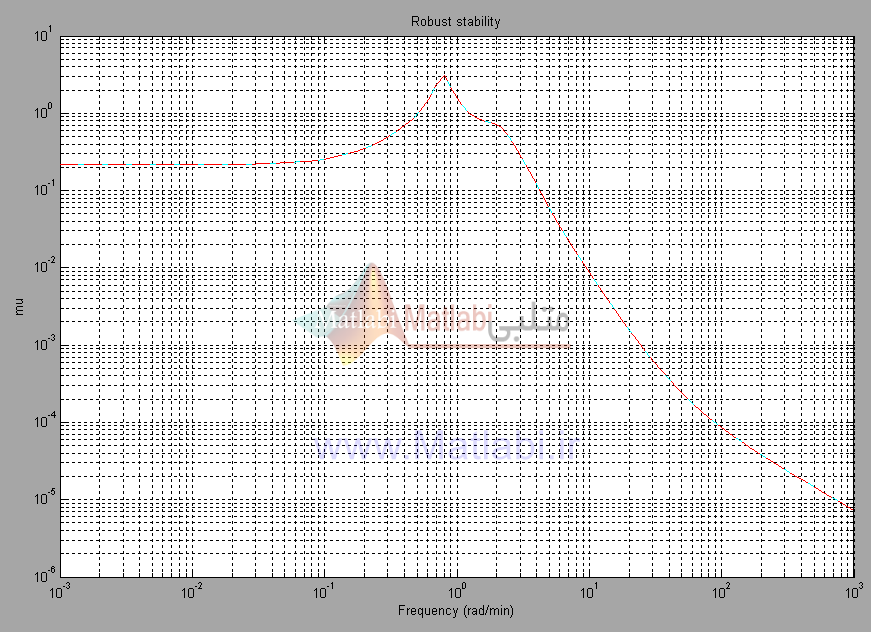
مشاهده مي شود که پايداري مقاوم سيستم با کنترل کننده طراحي شده تضمين مي شود.
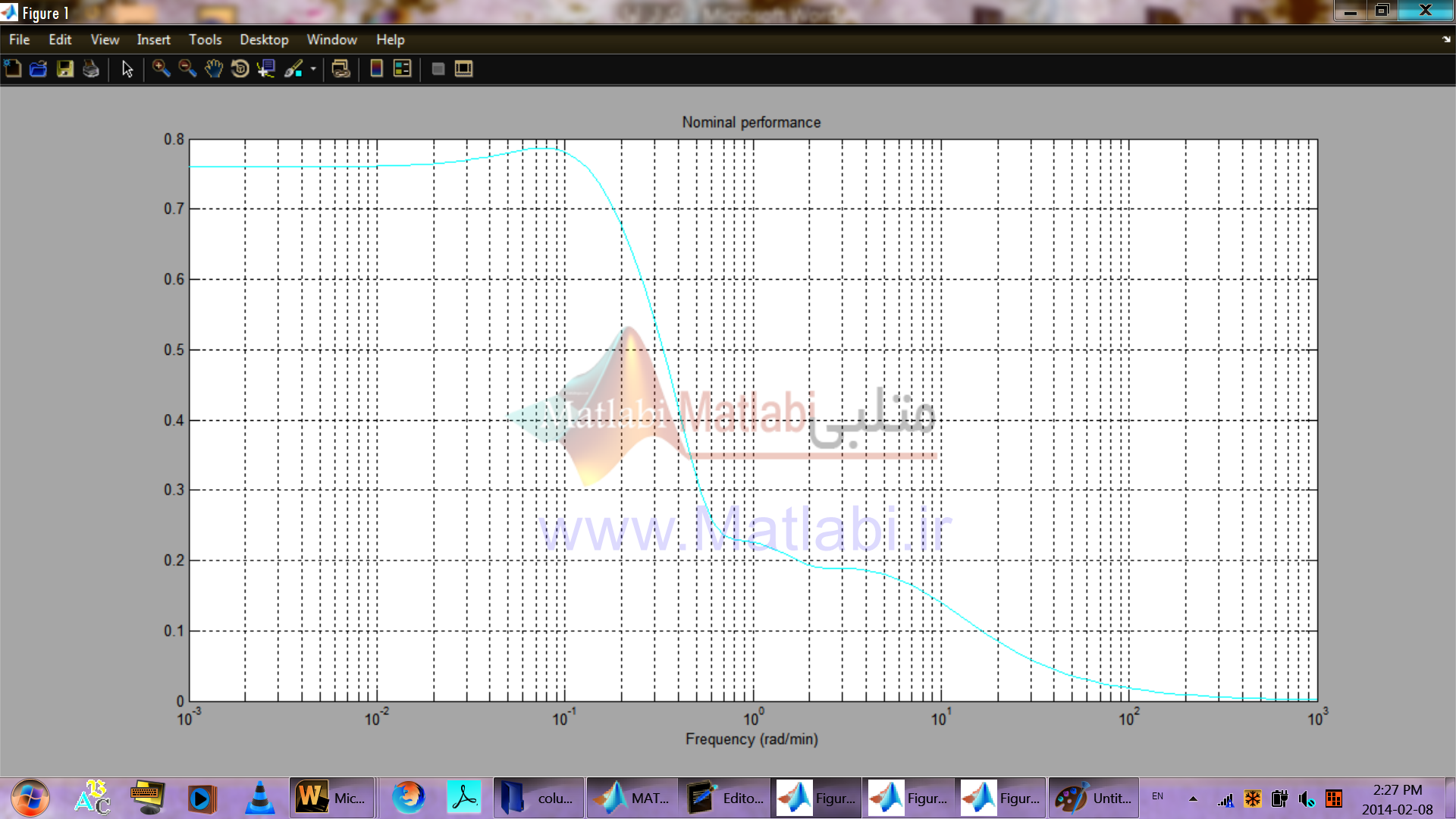
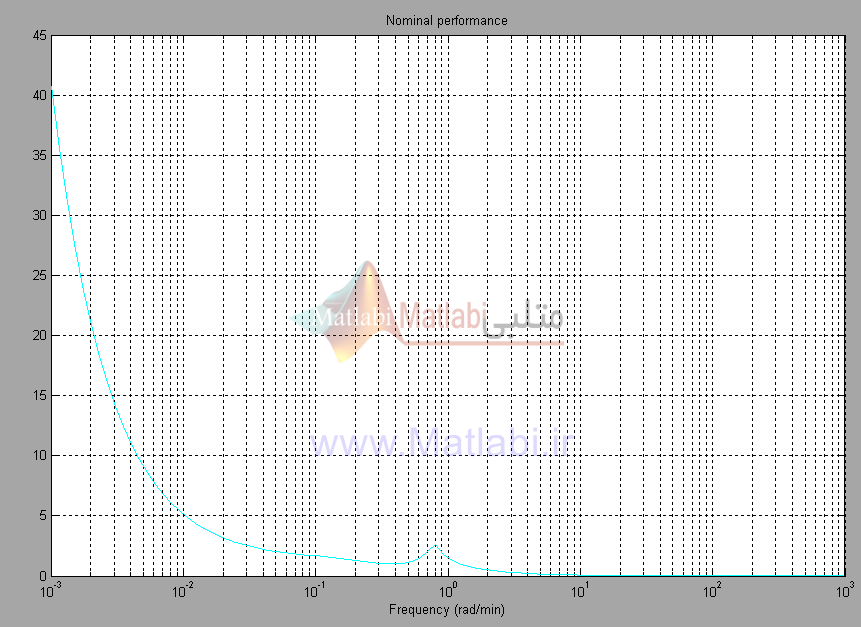
مشاهده مي شود که عملکرد نامي سيستم با کنترل کننده طراحي شده تضمين مي شود.
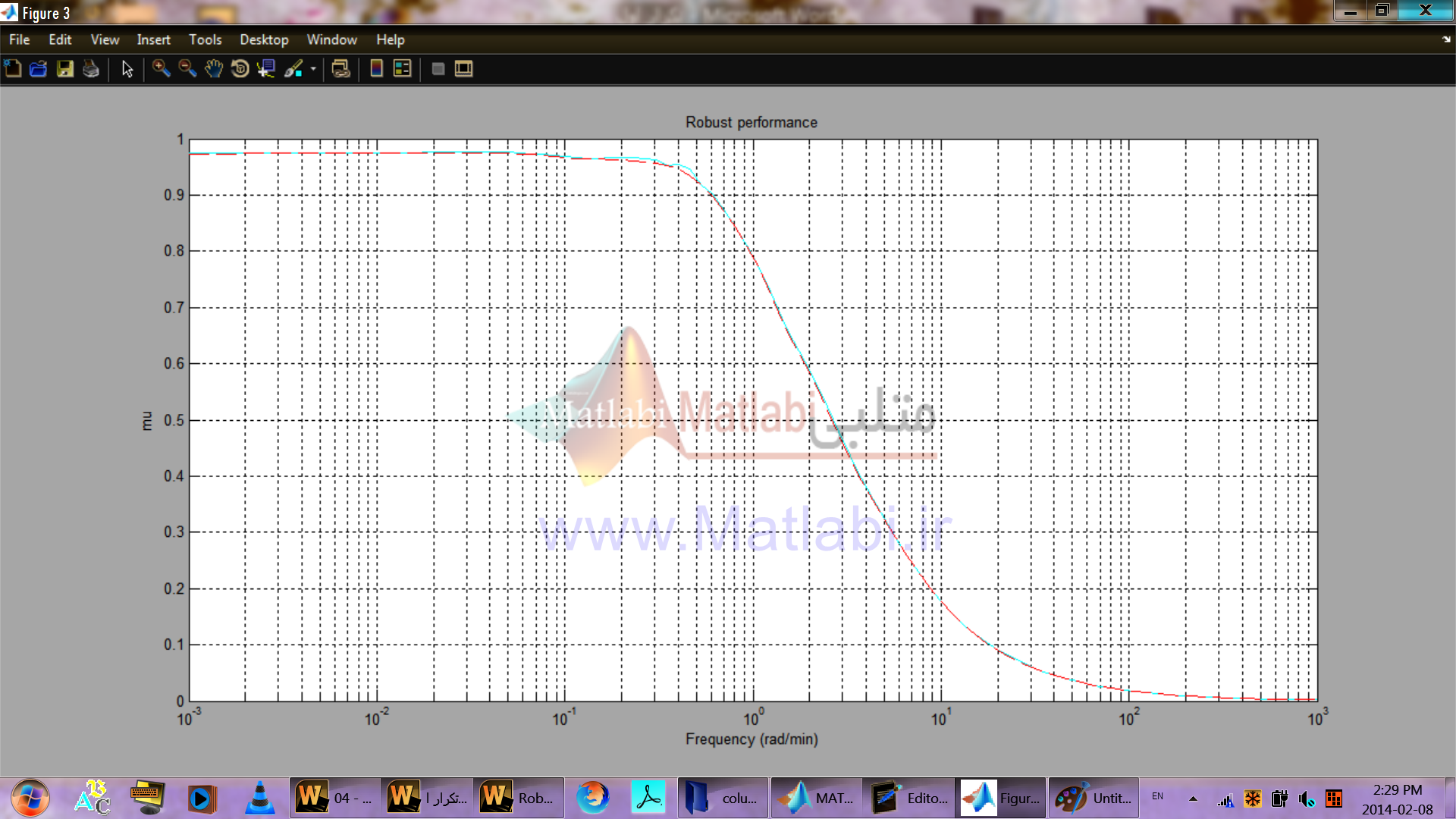
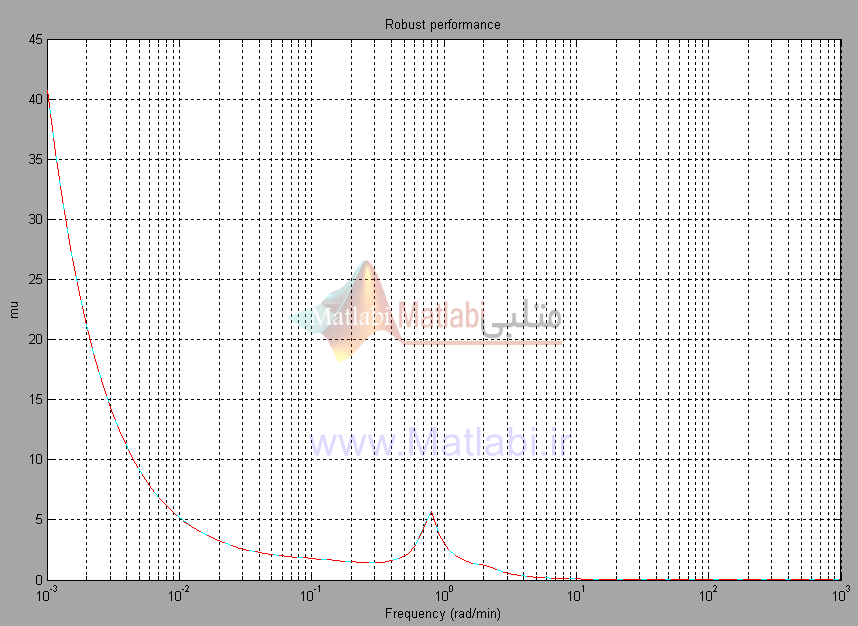
مشاهده مي شود که عملکرد مقاوم سيستم با کنترل کننده طراحي شده تضمين مي شود.
تحليل پاسخ گذرا سيستم حلقه بسته غير خطي با برنامه clp_col :
تحليل پاسخ گذرا سيستم غير خطي با کنترلر در حضور اغتشاش با برنامه prt_col :
ستون تقطير يك سيستم دو ورودي و دو خروجي با رفتار غيرخطي شديد بوده و بنابراين مدلسازي آن بسيار مشكل است.
تقطير فرآيند مهمي در جداسازي و خالص سازي مواد شيميايي ميباشد.
اكثر ستونهاي تقطير صنعتي براي جداسازي مخلوطهاي چند جزئي استفاده ميشوند كه در آنها مواد سازنده مخلوط كاملاً مشخص نميباشند .فرآيند تقطير به شدت غيرخطي بوده وبه دست آوردن مدلهاي تحليلي دقيق از ستونهاي تقطير با خلوص بالا در عمل امكانپذير نميباشد.
علت اين امر اين است كه روابط ترموديناميكي مربوط به تعادل بخار و آب، اطلاعات مربوط به خواص فيزيكي و ساير روابط ضروري براي توسعه مدل تحليلي اغلب موجود نمي باشند حتي با وجود داشتن چنين اطلاعاتي نيز مدلهاي تحليلي به دست آمده داراي معادلات ديفرانسيل معمولي غيرخطي هستند كه براي كار كنترلي مناسب نيست .
با درنظرگرفتن مشكلات ذكر شده مدل تجربي ميتواند جايگزين مناسبي براي مدل تحليلي درمدل سازي ستون تقطير باشد.
-
- مدلسازي نايقيني
نايقينيهاي در نظر گرفته شده براي سيستم کنترلي برج تقطير به صورت نايقيني در بهره (تلورانس) 20درصد و يک تاخير زماني تا يک دقيقه در هر کدام از کانالهاي ورودي ميباشد.
-
- مشخصات عملکردي سيستم حلقه بسته
هدف از طراحي سيستم کنترلي برج تقطير، مشخص کردن کنترل کنندهاي است که پايداري مقاوم و عملکرد مقاوم را براي پيکربندي LV تامين نمايد.
ما براي برآوردن اين نياز سعي ميکنيم از يک کنترلکنندهي شکلدهي حلقهي H* يک درجه آزادي و کنترل کنندهي ميو 2 درجه آزادي استفاده کنيم.
در مورد داده شده، پايداري مقاوم به معني تضمين پايداري سيستم حلقه بسته براي تمام:
و
است. خصوصيات حوزه زمان در دورهي پاسخ پلهي مورد نياز داده شده است که بايد به ازاي جميع مقادير K1 و K2 و تتا1 و تتا2 صادق باشد.
مخصوصا، براي يک ورودي پلهي واحد به اولين کانال ورودي در t=0، خروجي مقياس شدهي سيستم y1 (رديابي) و y2 (برهمکنش) بايد اغنا شوند:
و به طور مشابه، شرايطي مشابه براي ورودي پلهي واحد، در کنال ورودي دوم بايد اغنا گردد.
به علاوه، مشخصات حوزهي فرکانسي زير نيز بايد رعايت شوند:
که در آن Ky نشان دهندهي قسمت فيدبک کنترل کنندهي غير مقياس شده است. (در اينجا و در ادامه، يک متغيير با هد، اشاره به سيستم غير مقياس شده دارد.)
اين خصوصيات شامل بخش وسيعي براي جلوگيري از به اشباع رفتن ورودي هاي سيستم است.
2-
در بالا، سيگما بار به بزرگترين مقدار منفرد و تابع حساسيت G است.
شکل 5-1
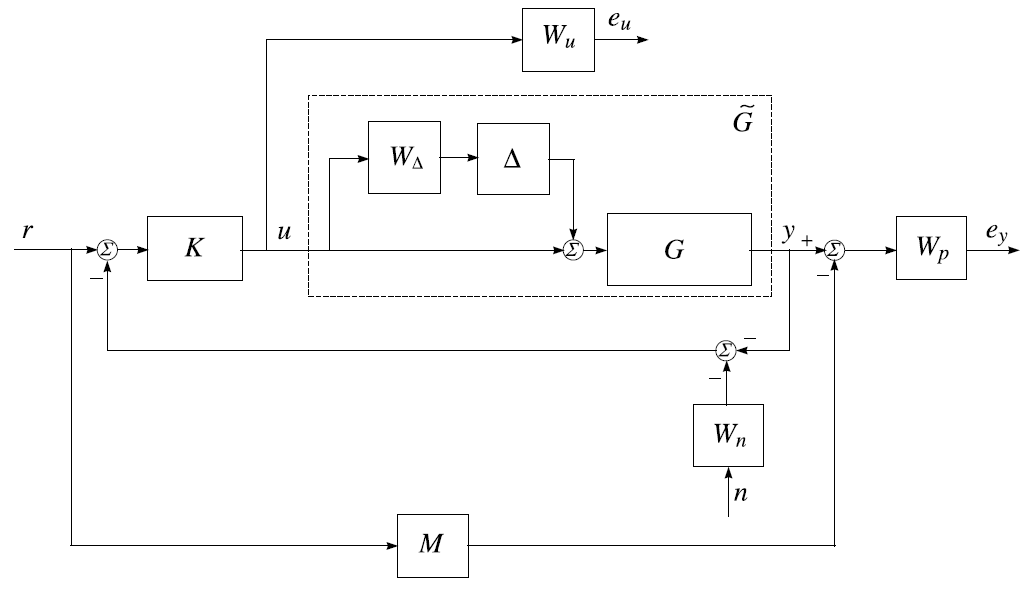
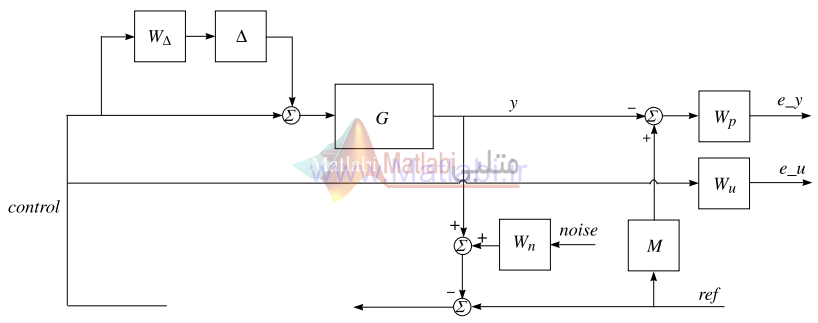
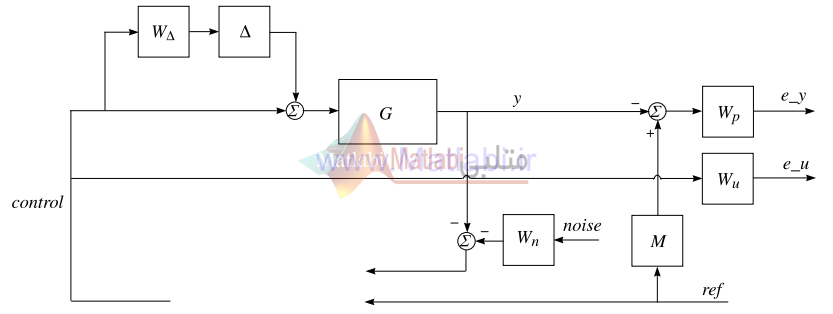
بلوک دياگرام سيستم حلقه بسته با کنترل کنندههاي يک و دو درجه آزادي، و ترکيب درنظر گرفتن ملزومات طراحي با وزن آنها، به ترتيب در شکلهاي 5-1 و 6-1 نشان داده شده است.
سيستم G توسط خط فاصلههاي مستطيل شکل نشان داده شده است، که شامل مدل مقياس شدهي عددي G به علاوهي نايقيني ضربي ورودي است. کنترل کنندهي K، از يک فيدبک از خروجي Yd و Xb و يک فيدفوروارد از سيگنال ورودي مرجع r است.
اندازهگيري ترکيب محصولات نهايي و مقطر شده توسط نويز n تخريب مي شود.
ديناميک مطلوب سيستم حلقه بسته، با انتخاب مناسب مدل M محقق ميشود.
مدل M، رفتار مطلوب ديناميکي سيستم حلقه بسته را از ورودي مرجع تا خروجي را نشان ميدهد. استفاده از يک مدل ديناميکي مطلوب به ما اجازه ميدهد مشخصات طراحي را به سرعت بدست آوريم.
ماتريس تابع تبديل انتخاب شدهي مدل M به صورت زير انتخاب شده است:
ضرايب تابع تبديل(T=6 و =0.8 ᶚ) در هر دو کانال به نوعي انتخاب شده اند که از ميرا شدن پاسخ با زمان نشست حدود 30 دقيقه مطمئن هستيم.
براي عناصر خارج از قطر اصلي در ماتريس انتقال براي کمينه کردن برهمکش بين کانالها مقدار صفر در نظر گرفتيم.
شکل 6-1
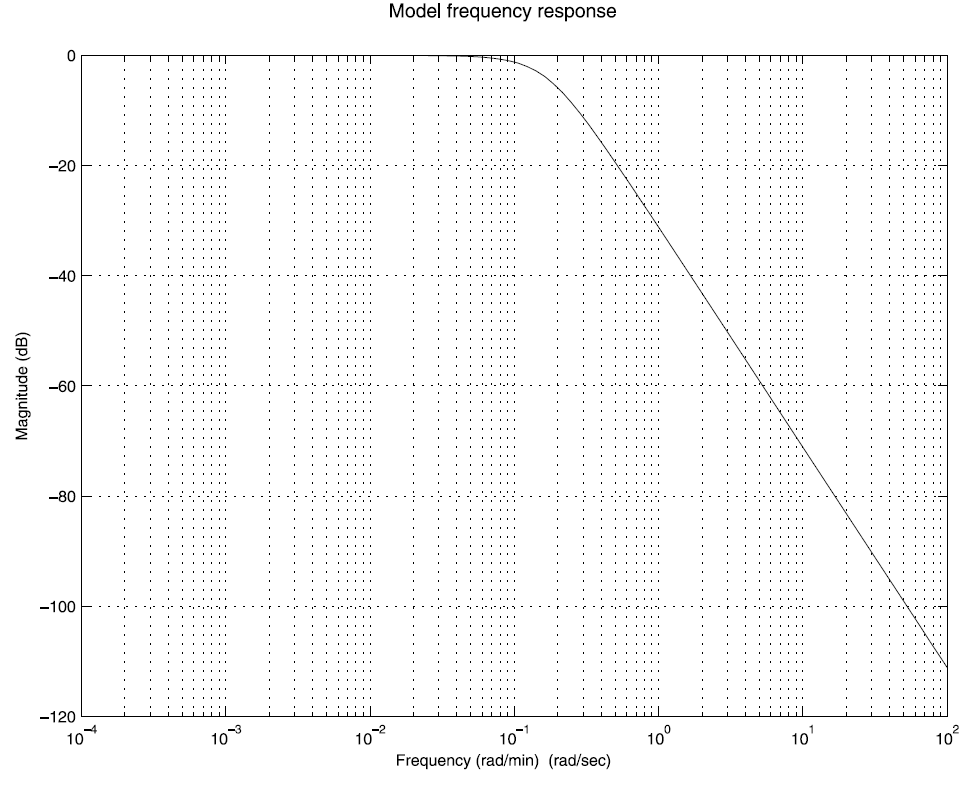
شکل 7-1
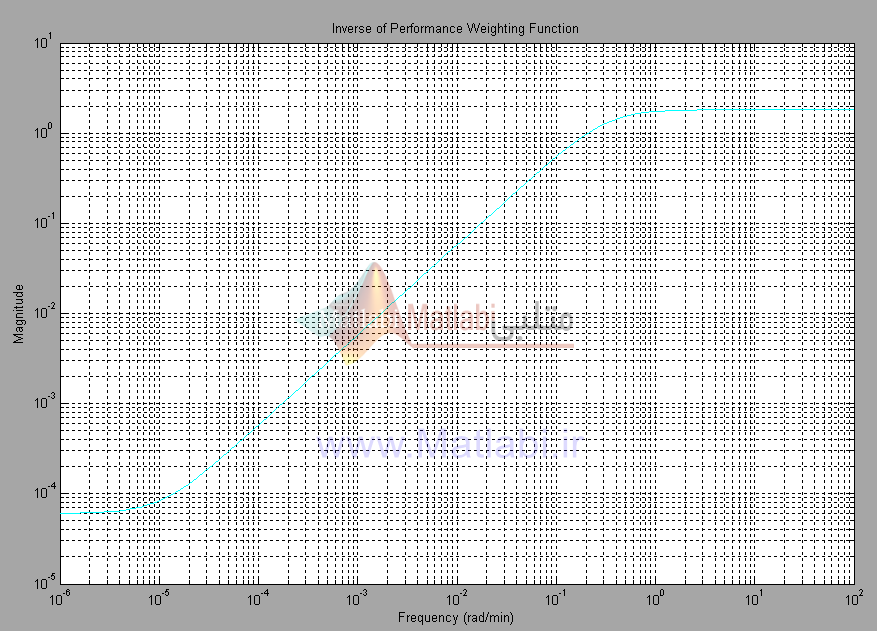
پاسخ فرکانسي مدل M در شکل 7-1 نشان داده شده است.
تابع تبديل مدل، توابع وزندهي کنترل و عملکرد بعلاوه فيلتر شکلدهي نويز همگي در فايل wts_col.m تنظيم ميشوند.
5-16. ارتباطات سيستم حلقه بسته و حلقه باز
ارتباطات سيستم حلقه باز براي هر دو نوع کنترلر توسط ام فايل با نام olp.col بدست ميآيد.
ساختار داخلي سيستم حلقه باز مرتبه 22 با شش ورودي و شش خروجي و با کنترلر يک درجه آزادي که بصورت متغير sys_ic_1dof ذخيره شده است، در شکل 11-16 نمايش داده شده است.
رفرنسها و نويزها به ترتيب بصورت متغيرهاي ref و noise و کنترلرها نيز با نام متغير control ذخيره شدند.
همه متغير دو المان دارند (بردارهاي دو بعدي هستند).
دياگرام شماتيک نشان دهنده ترتيب ورودي/خروجي براي متغير sys_ic_1dof در شکل 12-16 نشان داده شده است.
شکل 11-16. ساختار ارتباطات حلقه باز سيستم ستون تقطير براي کنترلر يک درجه آزادي
شکل 13-16. ساختار ارتباطات حلقه باز سيستم ستون تقطير براي کنترلر دو درجه آزادي
ساختار داخلي سيستم حلقه باز مرتبه 22 شش ورودي، هشت خروجي با کنترلر 2dof که بصورت متغير sys_ic_2dof ذخيره شده در شکل 13-16 نمايش داده شده است.
دياگرام شماتيک نشان دهنده ترتيب ورودي/خروجي ويژه براي متغير sys_ic_2dof در شکل 14-16 نمايش داده شده است.
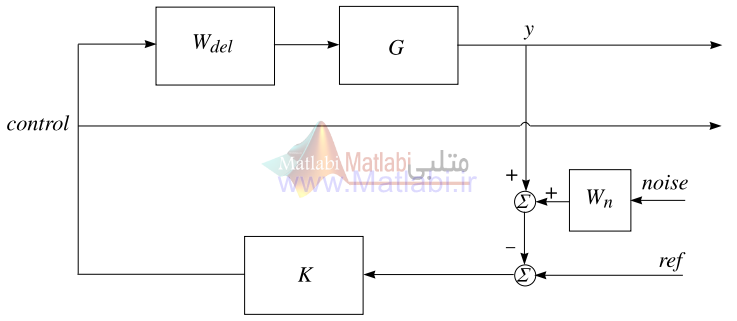
شکل 15-16. ساختار ارتباطات حلقه بسته سيستم ستون تقطير براي کنترلر 1dof
بلوک دياگرام مورد استفاده در شبيهسازي سيستم حلقه بسته با کنترلر 1dof در شکل 15-16. مشان داده شده است.
ارتباطات حلقه بسته متناظر، در متغير clp_ic ذخيره شدند. تاخيرهاي نايقيني بوسيله ماتريس تابع تبديل بيان ميشوند.
جاييکه و يک تقريب مرتبه ششم از تاخير زماني ميباشد.
دياگرام شماتيک نشاندهنده ترتيب خاص ورودي/خروجي براي متغير clp_ic در شکل 16-16 نشان داده شده است.
بلوک دياگرام مورد استفاده در شبيهسازي سيستم حلقه بسته با کنترلر 1dof، در شکل 17-16 و دياگرام شماتيک نشان دهنده ترتيب خاص ورودي/ خروجي متغير clp_ic در شکل 18-16 نمايش داده شده است.
شکل 17-16. ساختار ارتباطات حلقه بسته سيستم ستون تقطير براي کنترلر 1dof
6-16. طراحي کنترلر
طراحي موفق سيستم کنترل ستون تقطير ميتواند با استفاده از پروسه طراحي شکلدهي حلقه (LSDP) و تحليل- بدست آيد.
توجه کنيد که در مورد LSDP، ما از خصوصيات عملکردي اجرا شده در مورد تحليل- استفاده نخواهيم کرد.
در عوض بجاي آن، از يک پيش فيلتر W1 و يک پس فيلتر W2 به منظور شکل مناسبتر تابع تبديل حلقه باز W1G W2 بهره ميبريم.
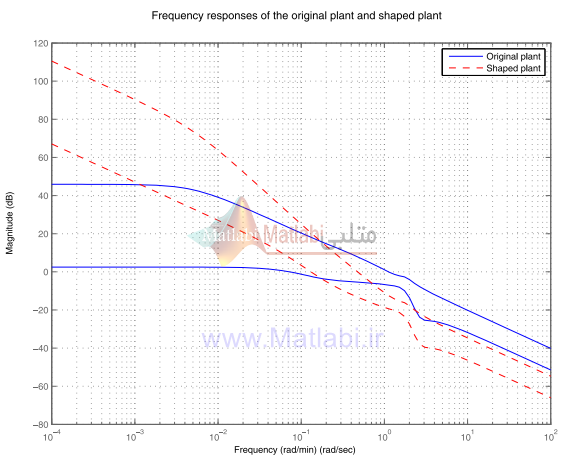
شکل 19-16. مقادير ويژه سيستم شکلدهي شده و اصلي
1-6-16. طراحي شکلدهي حلقه
در مورد مذکور ما يک پيشفيلتر با تابع تبديل زير انتخاب ميکنيم:
انتخاب بهره معادل با 7/1 براي اطمينان از به اندازه کافي کوچک بودن خطاي حالت پايدار انجام ميشود.
بهره بزرگتر منجر به خطاهاي حالت ماندگار کوچکتر ميشود ولي پاسخ گذرا را بد ميکند.
پس فيلتر بصورت W2=I2 در نظر گرفته ميشود. نمودارهاي مقدار ويژه سيستمهاي شکلدهي شده و اصلي در شکل 19-16 نشان داده شدهاند.
طراحي کنترلر LSDP يک درجه آزادي بوسيله ام فايل با نام lsh_col.m انجام ميشود که تابع ncfsyn را اجرا ميکند.
کنترل بدست آمده از مرتبه نه است.
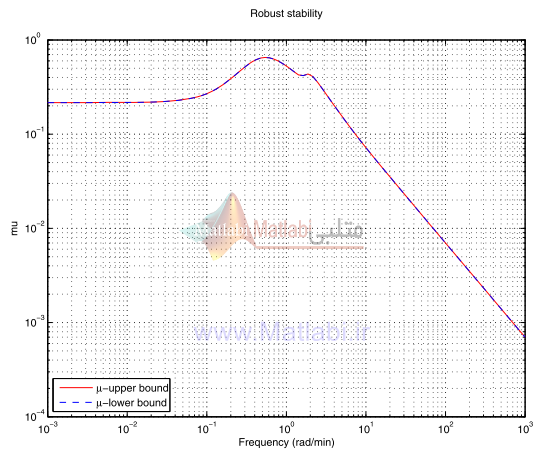
آناليز پايداري مقاوم سيستم حلقه بسته توسط فايل mu_col انجام ميشود. بعنوان مثال اين آناليز، گزارش زير را بدست ميدهد:
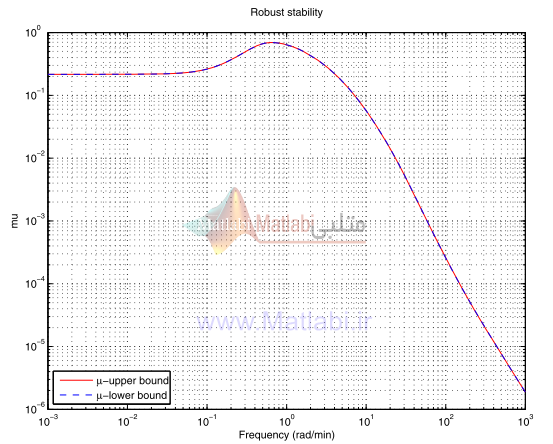
شکل 20-16. پايداري مقاوم کنترلر شکلدهي حلقه
ترسيم پاسخ فرکانسي مقدار ساخت يافته با توجه به پايداري مقاوم در شکل 20-16 نشان داده شده است.
سيستم حلقه بسته پايداري را براي همه اختلالات و آشفتگيهاي با نرم کمتر از 54/1 حفظ مينمايد.
بطور معمول احتياجات و اقتضائات براي عملکرد نامي و عملکرد مقاوم، بوسيله اين کنترلر انجام نميشوند.
پاسخ فرکانسي حلقه بسته توسط فايل frs_col.m بدست ميآيد.
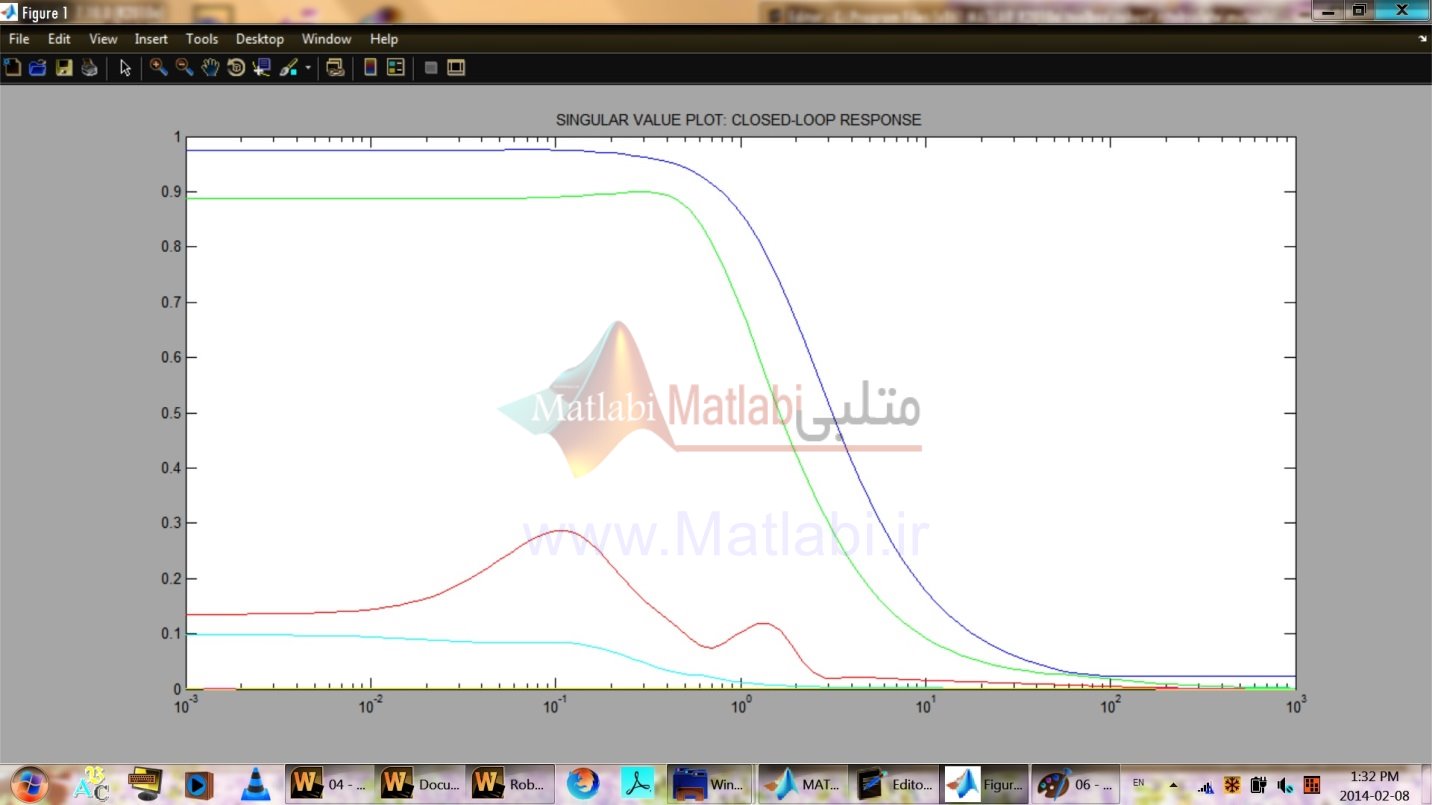
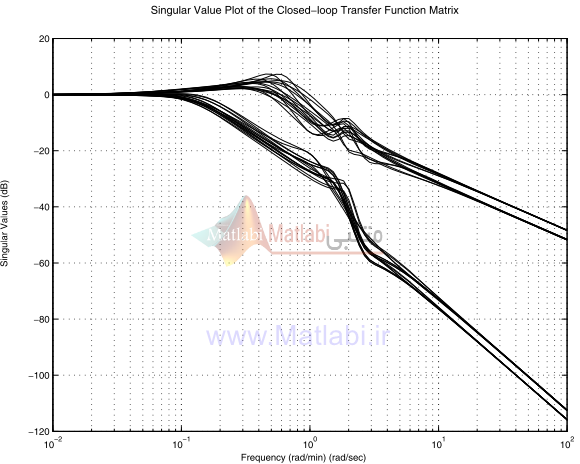
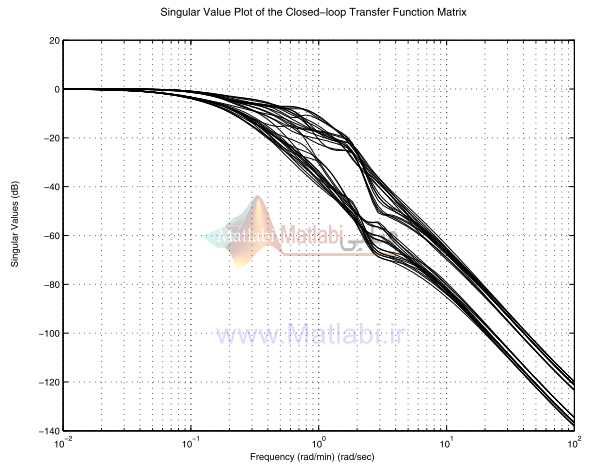
ترسيم مقدار تكين تابع تبديل سيستم حلقه بسته مقياس بندي نشده در شکل 21-16 نشان داده شده.
هر دو بهرههاي فرکانس پايين برابر يک هستندکه صفر شدن خطاي حالت ماندگار در هر دو کانال را تضمين ميکند.
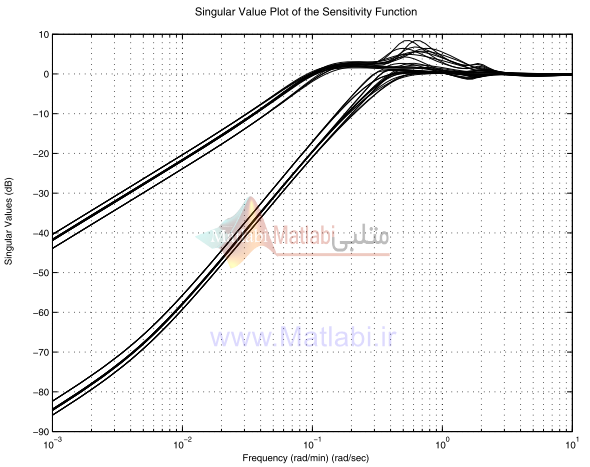
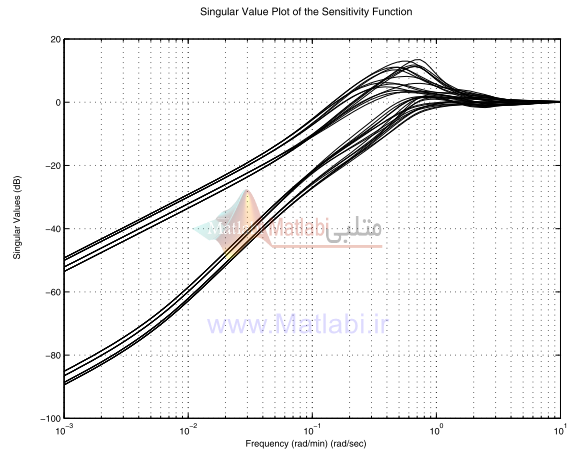
در شکل 22-16 ما ترسيم مقدار ويژه حساسيت مقياسبندي نشده را نشان داديم.
شکل 21-16. پاسخ فرکانسي سيستم حلقه بسته با کنترلر شکلدهي حلقه
شکل 22-16. پاسخ فرکانسي تابع حساسيت
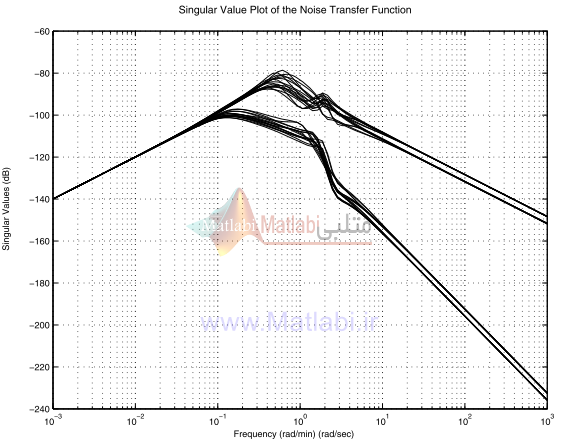
شکل 23-16. پاسخ فرکانسي نويزها
ترسيمهاي مقدار ويژه ماتريس تابع تبديل با توجه به نويزها (شکل 23-16)، نشان از تضعيف حداقل 104 برابري نويزها در خروجي سيستم ميدهند. ترسيمهاي مقدار ويژه ماتريسهاي تابع تبديل و به ترتيب در شکلهاي 24-16 و 25-16 نشان داده شدند.
ماکزيمم بزرگترين مقدار ويژه براي به مراتب کمتر از يک است و بزرگترين مقدار ويژه کمتر از 200 است در حالتيکه خصوصيات حوزه فرکانسي مربوطه بدست مي آيد.
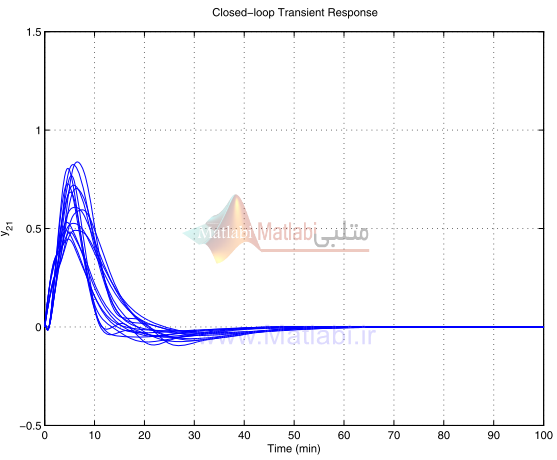
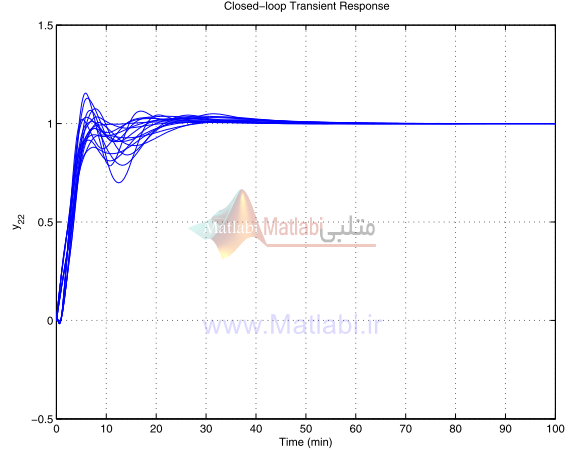
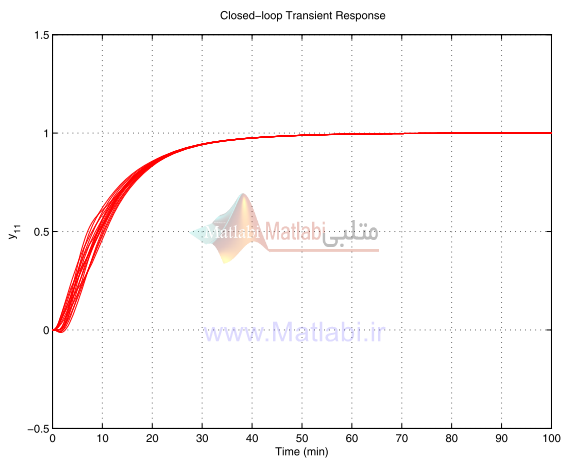
در شکلهاي 26-16 الي 29-16 ما پاسخ گذراي سيستم حلقه بسته مقياس بندي شده، براي مقادير مختلف بهره نايقيني و تاخير زماني را که بوسيله فايل mcs_col.m نتيجه شده، نشان ميدهيم.
مشخصات حوزه زمان حاصل ميشود و پاسخ گذراي سيستم حلقه بسته يک زمان نشست[40] کوچک دارد.
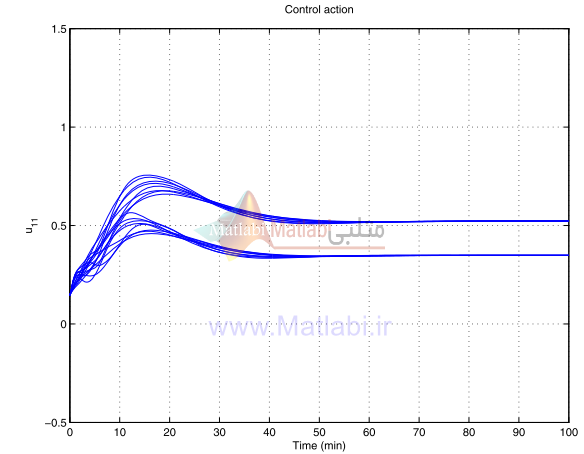
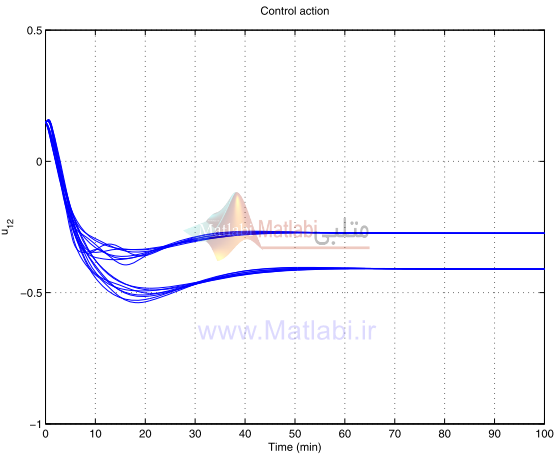
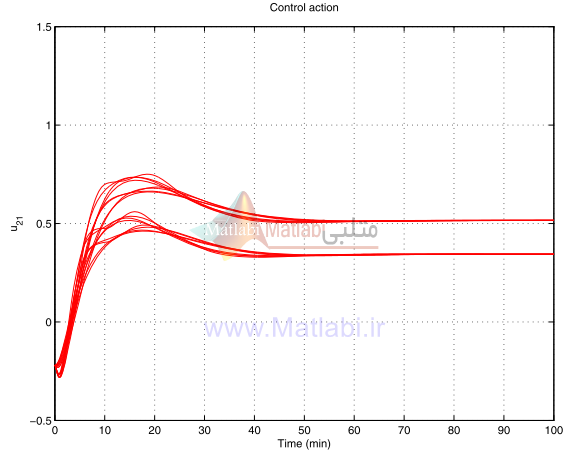
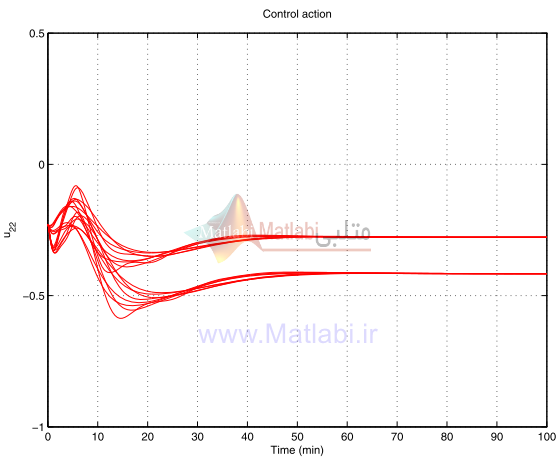
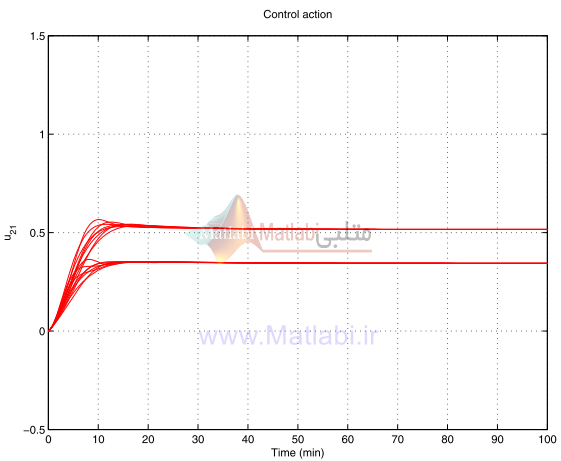
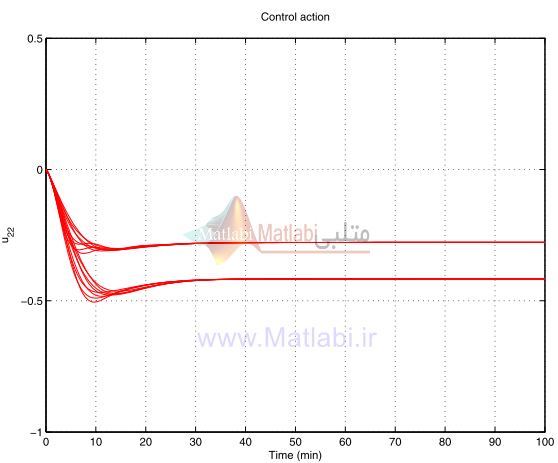
عمل کنترل در سيستم حلقه بسته براي همان متغيرهاي پارامترهاي نايقيني در شکل 30-16 الي 33-16 نشان داده شده است.
2-6-16. تحليل-
فرض کنيد P(s) ماتريس تابع تبديل سيستم حلقه باز شش ورودي، هشت خروجي شامل مدل ستون تقطير بعلاوه تابع وزندهي باشد و ساختار بلوک بصورت زير بيان شود:
شکل 24-16.ترسيم مقدار ويژه
شکل 25-16.ترسيم مقدار ويژه
شکل 26-16. پاسخ گذراي آشفتهشده y11 براي کنترلر شکلدهي حلقه
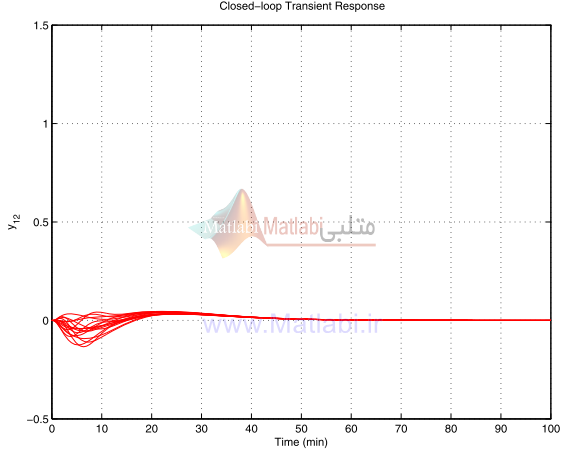
شکل 27-16. پاسخ گذراي آشفتهشده y12 براي کنترلر شکلدهي حلقه
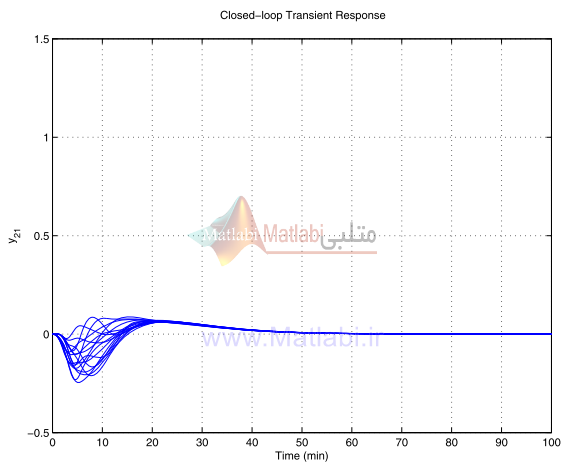
شکل 28-16. پاسخ گذراي آشفتهشده y21 براي کنترلر شکلدهي حلقه
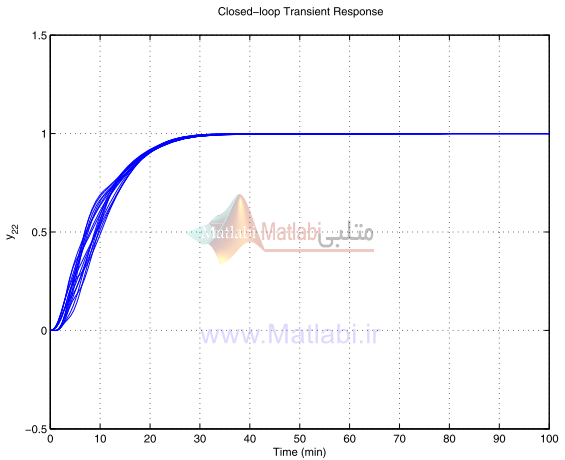
شکل 29-16. پاسخ گذراي آشفتهشده y22 براي کنترلر شکلدهي حلقه
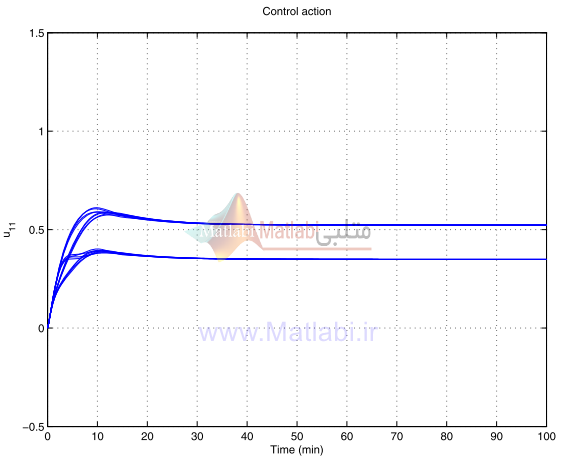
شکل 30-16. عمل کنترلي آشفتهشده u11 براي کنترلر شکلدهي حلقه
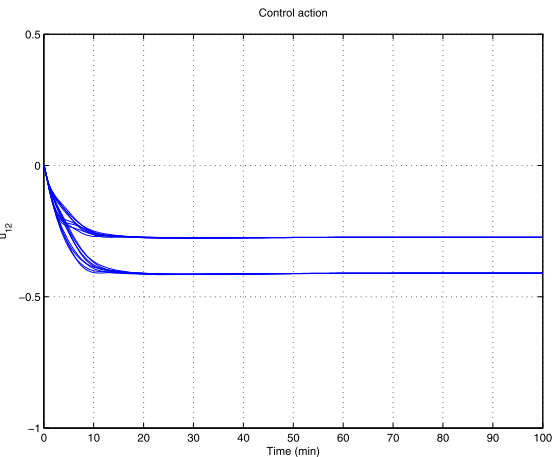
شکل 31-16. عمل کنترلي آشفتهشده u12 براي کنترلر شکلدهي حلقه
شکل 32-16. عمل کنترلي آشفتهشده u21 براي کنترلر شکلدهي حلقه
شکل 33-16. عمل کنترلي آشفتهشده u22 براي کنترلر شکلدهي حلقه
| تکرار | مرتبه کنترلر | ماکزيمم مقدار |
| 1 | 22 | 091/1 |
| 2 | 28 | 991/0 |
| 3 | 28 | 978/0 |
جدول 3-16. نتايج تحليل-
بلوک اول اين ماتريس مربوط به بلوک نايقيني است که در مدلسازي نايقيني ستون تقطير بکار ميرود.
دومين بلوک يک بلوک نايقيني ساختگي است که براي شامل شدن اهداف عملکردي در فريم کاري روش بيان شده است.
وروديها به اين بلوک، سيگنالهاي خطاي وزندهي شده و هستند. خروجيها، وروديهاي r و n بيروني هستند.
در مواجهه با اهداف طراحي، يک کنترلر پايدار کننده دو درجه آزادي بايد يافت شود بطوريکه در هر فرکانس ، مقدار ويژه ساخت يافته وضعيت
را ارضا نمايد.حصول اين وضعيت عملکرد سيستم حلقه بسته را تضمين ميکند. بعنوان مثال:
تحليل- با استفاده از ام فايل ms_col.m که تابع dkitopt را اجرا ميکند انجام ميشود.
پروسه تکرار D-K در جدول 3-16 نشان داده شده است.
در مورد مذکور بعد از حلقه D-K سوم، يک کنترلر مناسب بدست ميآيد. کنترلر پايدار و از مرتبه 28 ميباشد.
از جدول 3-16 مشاهده ميشود که بعد از سومين تکرار، ماکزيمم مقدار برابر 978/0 است.
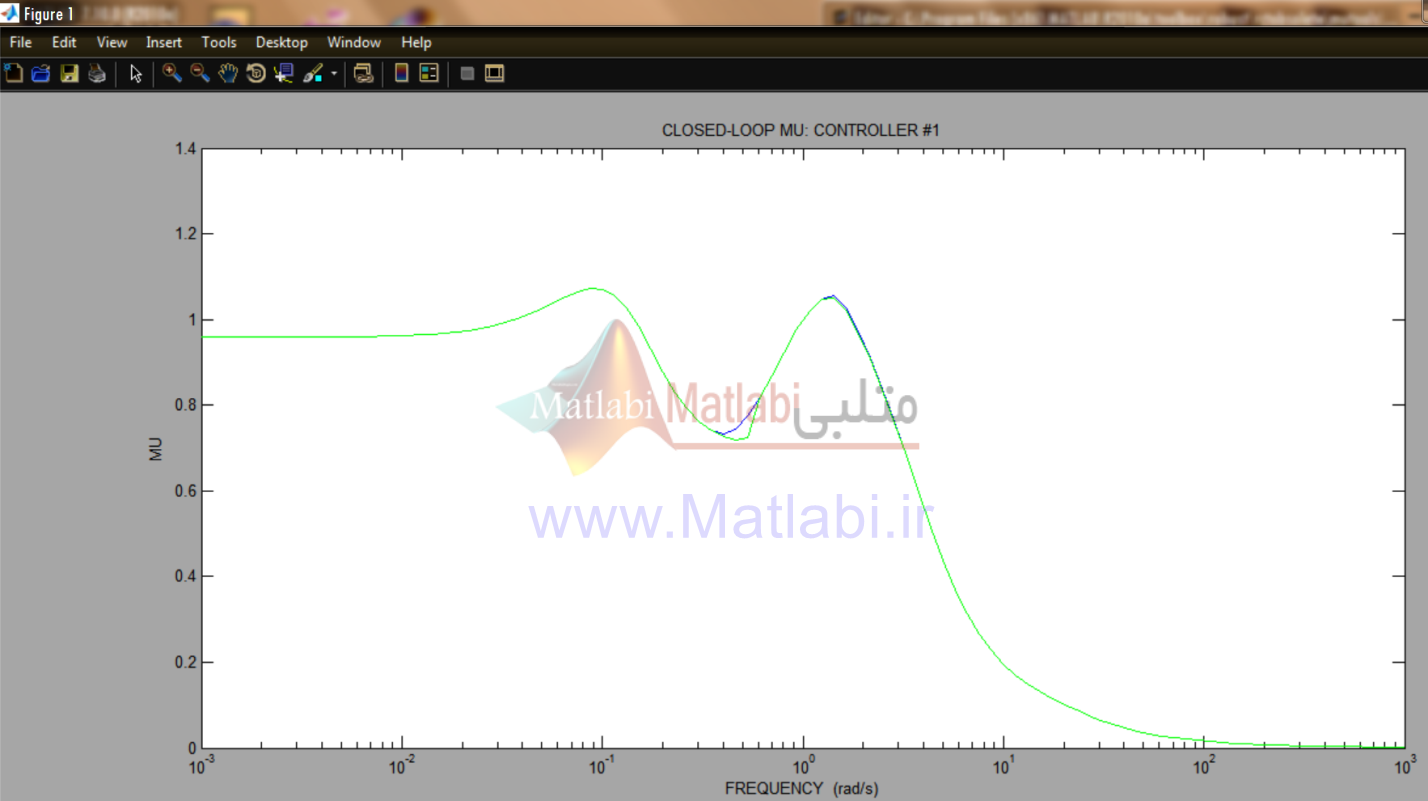
تحليل- سيستم حلقه بسته بوسيله فايل mu_col انجام ميشود. بر طبق گزارشهاي ذيل، سيستم به عملکرد مقاوم و پايداري مقاوم دست پيدا ميکند.
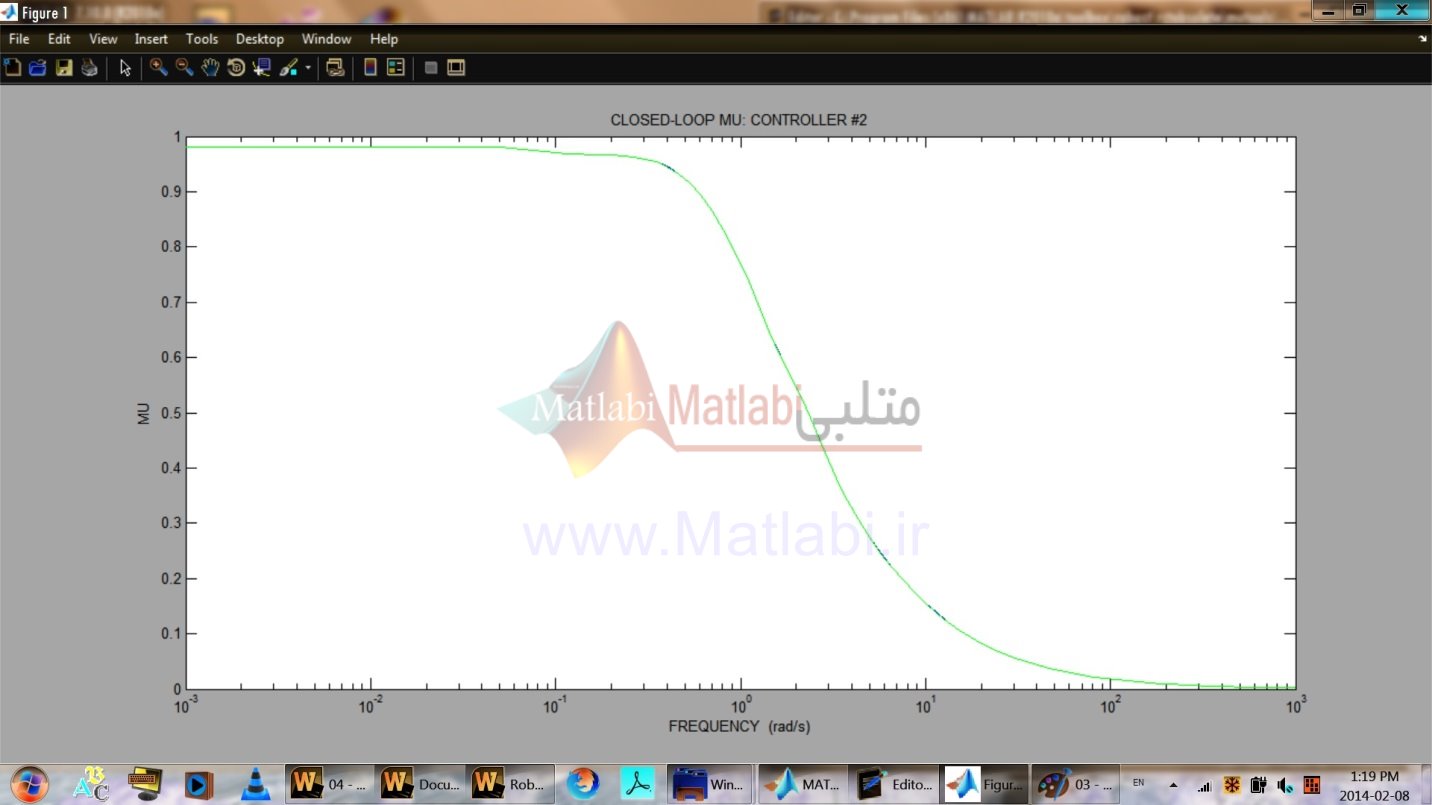
شکل 34-16. پايداري مقاوم براي کنترلر
ترسيم پاسخ فرکانسي مقدار ويژه ساخت يافته براي بررسي پايداري مقاوم در شکل 34-16 نشان داده شده است.
پايداري سيستم تحت اختلالات و آشفتگيهايي که شرط را ارضا ميکنند، حفظ ميشود.
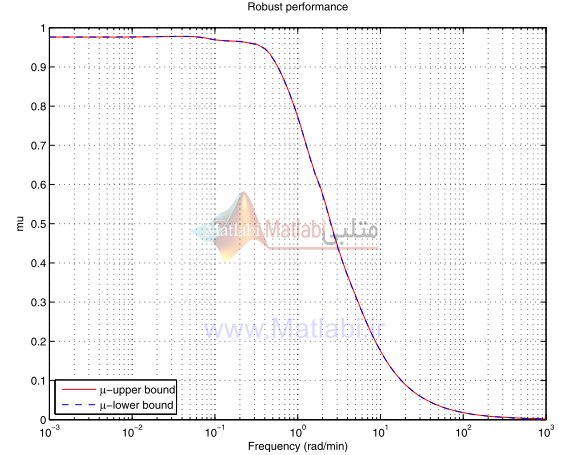
پاسخ فرکانسي به منظور تحليل عملکرد مقاوم در شکل 35-16 نشان داده شده است.
زمانيکه سيستم حلقه بسته به عملکرد مقاوم ميرسد، ماکزيمم مقدار برابر 978/0 ميشود.
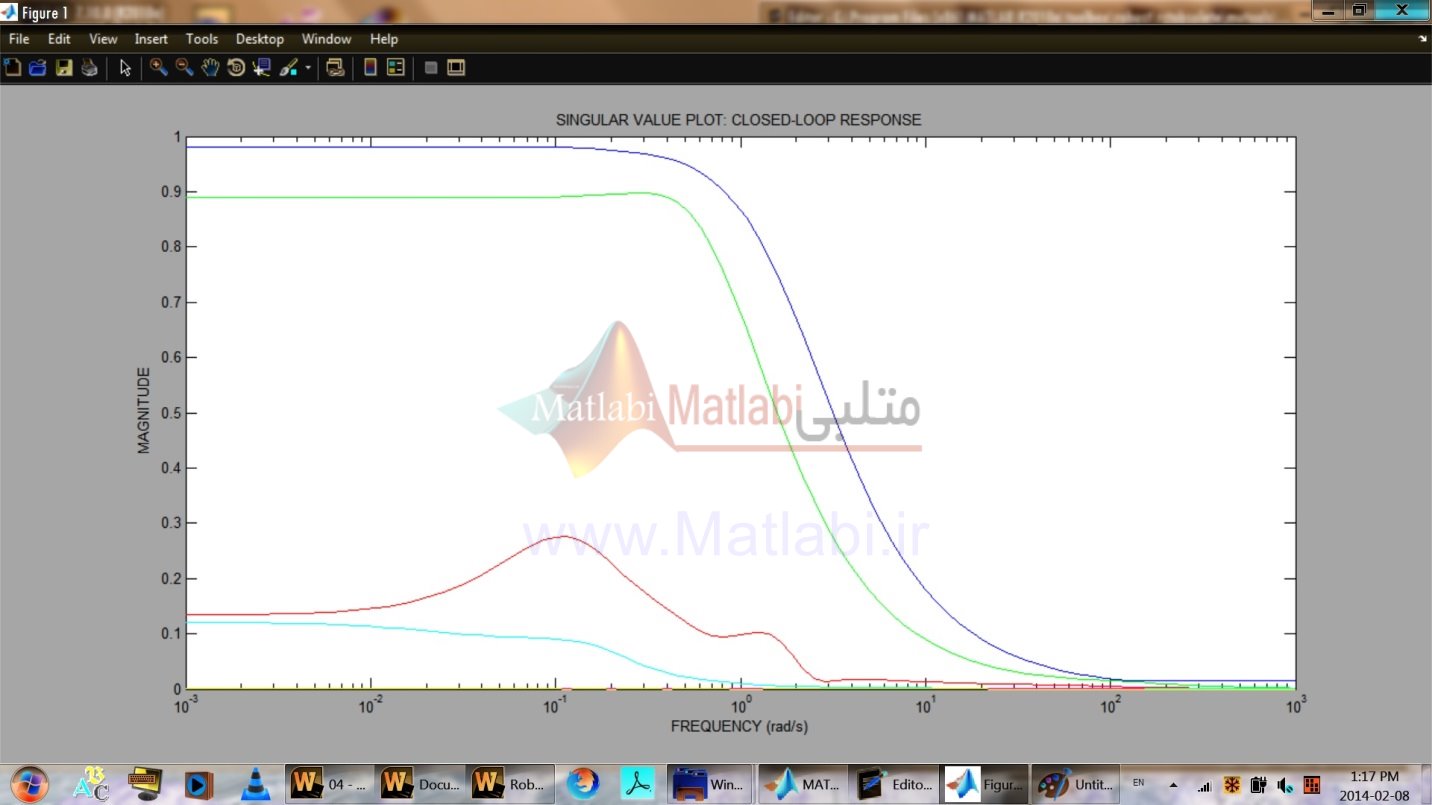
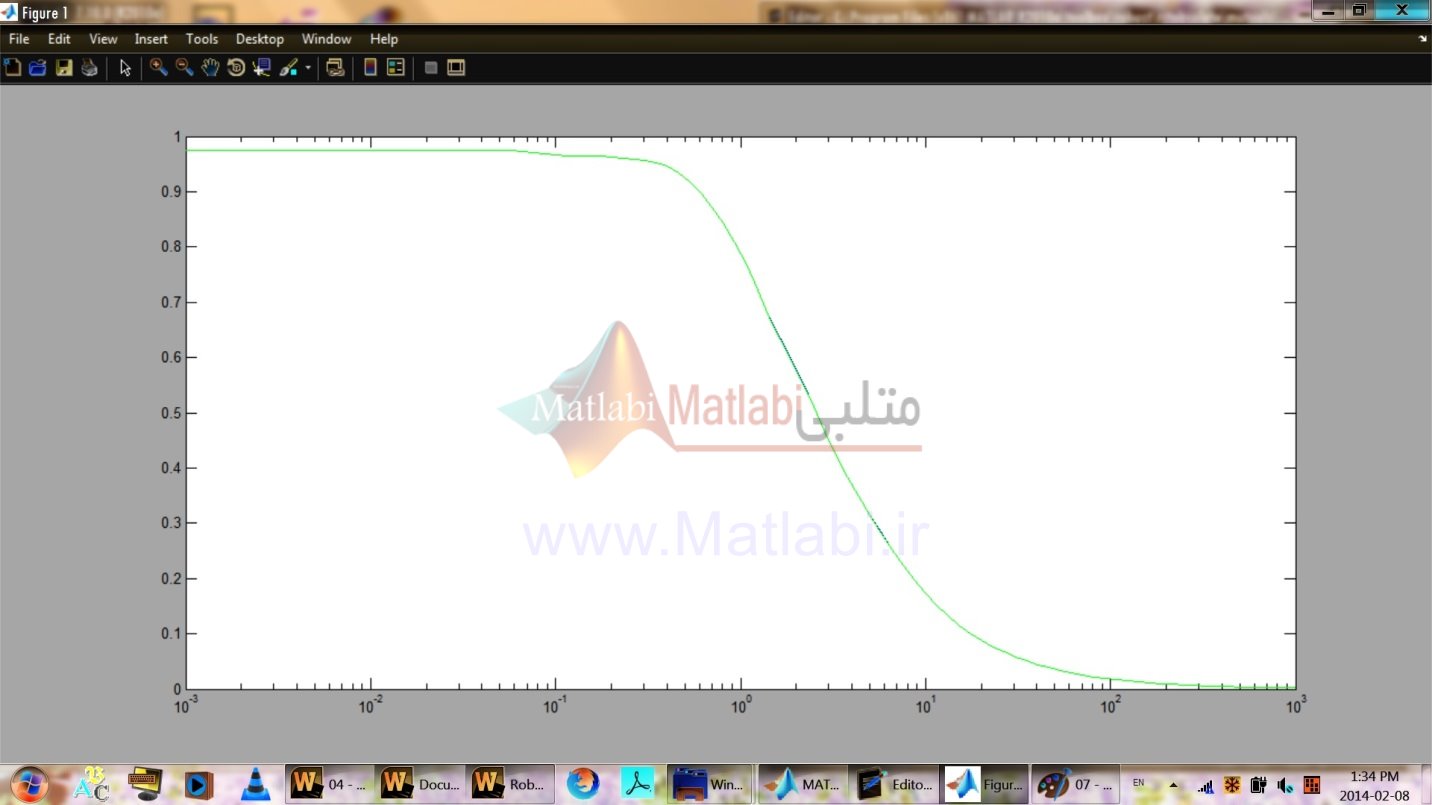
ترسيم مقدار ويژه سيستم حلقه بسته مقياسگذاري نشده، در شکل 36-16 نشان داده شده است.
پهناي باند سيستم حلقه بسته تقريبا است.
در شکل 37-16ما ترسيم مقدار ويژه تابع حساسيت مقياسگذاري نشده را نشان ميدهيم.
شکل 35-16. عملکرد مقاوم براي کنترلر ؟؟
شکل 36-16. ترسيمهاي مقدار ويژه حلقه بسته
شکل 37-16. پاسخ فرکانسي تابع حساسيت
پاسخهاي فرکانسي در حضور نويز در شکل 38-16 نشان داده شدند. از شکل اين استنباط ميشود که نويزهاي موجود در اندازهگيري تقطير و ترکيب محصول تحتاني، تاثير ناچيزي روي خروجي سيستم دارند.
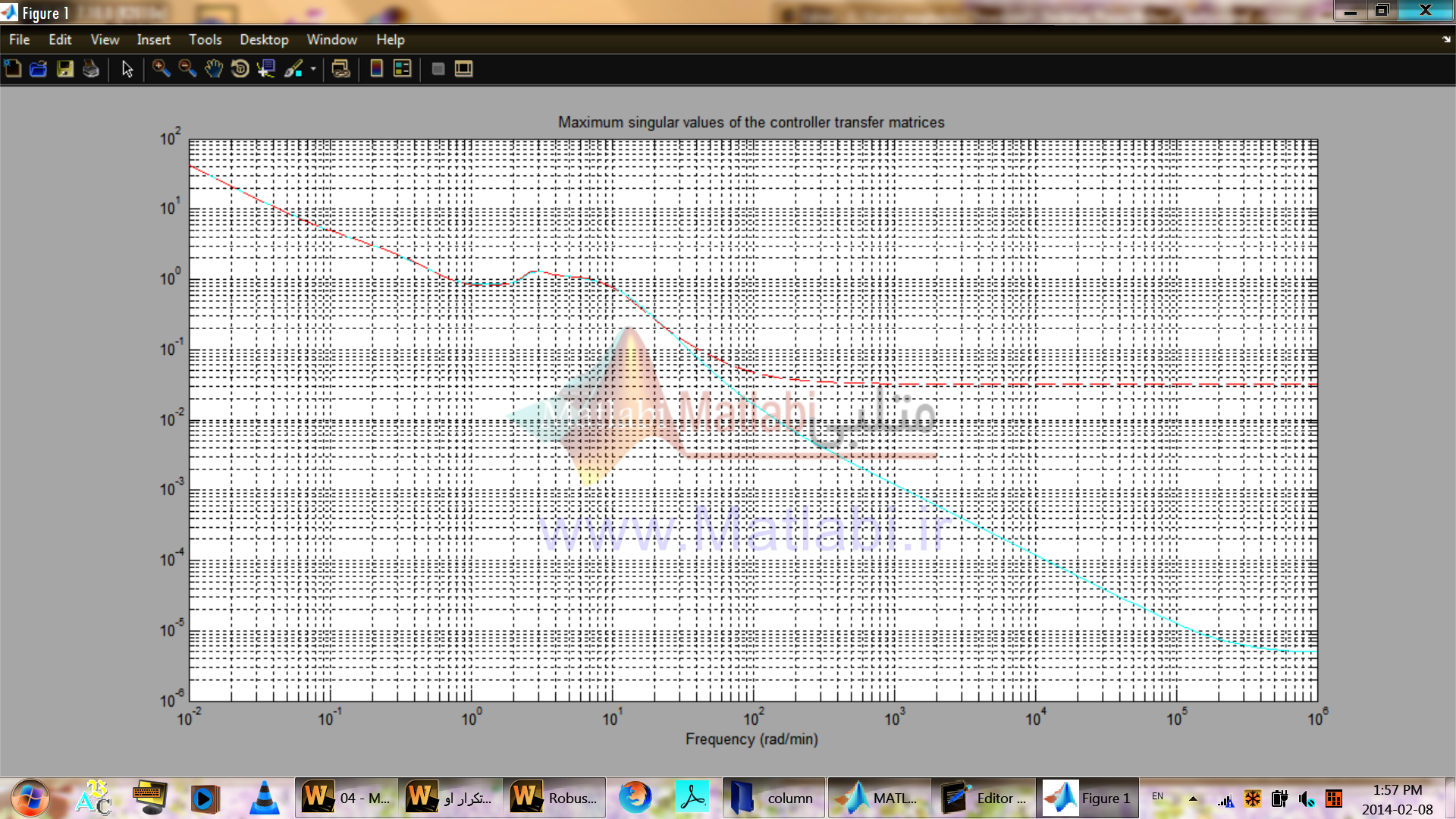
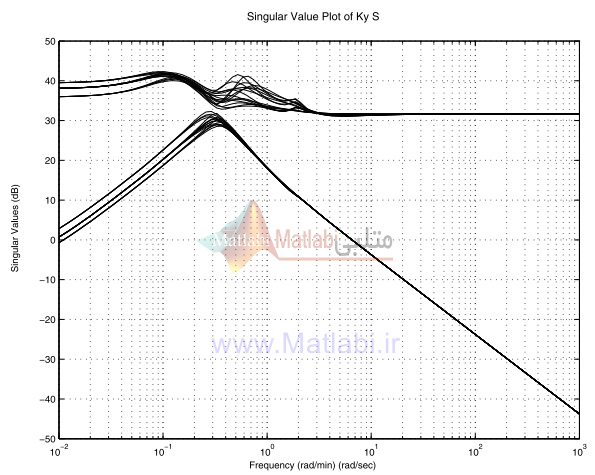
ترسيم مقادير ويژه کنترلر- مقياسبندي نشده، در شکل 39-16 نشان داده شده است.
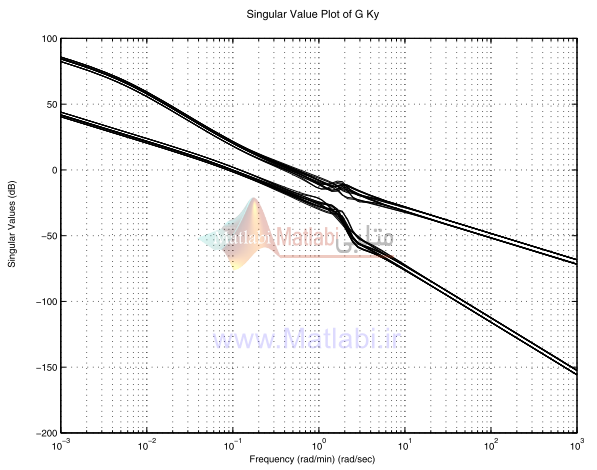
ترسيمهاي مقدار ويژه و به ترتيب در شکلهاي 40-16 و 41-16 نمايش داده شدند.
ماکزيمم بزرگترين مقدار ويژه براي کمتر از يک است و ماکزيمم بزرگترين مقدار ويژه کمتر از 300 است.
بنابراين مشخصات حوزه فرکانسي بدست مي آيد.
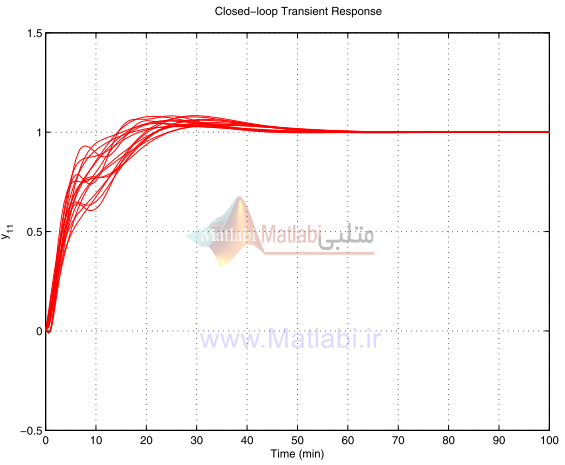
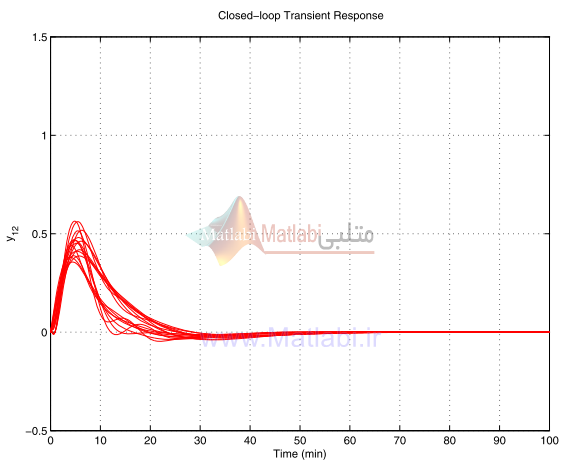
پاسخ گذراي آشفته سيستم حلقه بسته مقياسگذاري شده با يک کنترلر- در شکلهاي 42-16 الي 45-16 نشان داده ميشود.
پاسخها به رفرنسهاي مربوطه هيچ جهشي ندارند و اثر متقابل کانالها ضعيفتر از حالتي است که کنترلر شکلدهي حلقه بکار رفت.
عمل کنترل در مورد سيستم آشفته با کنترلر- در شکلهاي 46-16 الي 49-16 نشان داده شده است.
حالا کنترلر کاهش مرتبه را در نظر بگيريد. براي اين هدف ما ام فايل red_col.m را اجرا ميکنيم.
با استفاده از تابع reduce مرتبه کنترلر به 12 کاهش مييابد.
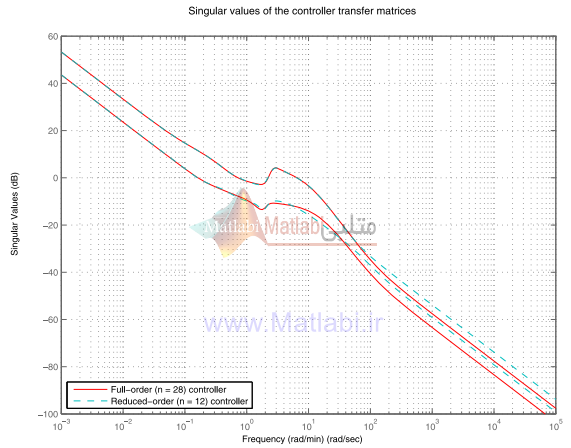
در شکل 50-16 ما پاسخهاي فرکانسي ماکزيمم مقادير ويژه کنترلرهاي کاهش مرتبه يافته و مرتبه کامل مقياسگذاري شده را با هم مقايسه ميکنيم. پاسخهاي فرکانسي هر دو کنترلرهاي مرتبه کامل و کاهش مرتبه يافته تا منطبق بر هم هستند که خيلي بيشتر از پهناي باند حلقه بسته سيستم است. به همين دليل پاسخ هاي گذراي سيستم حلقه بسته با کنترلرهاي مرتبه کامل و کاهش مرتبه يافته در عمل غير قابل تشخيص هستند.
شکل 42-16. پاسخ هاي گذراي آشفته شده Y12 براي کنترلر μ
شکل 43-16 پاسخ گذراي آشفته شده Y12 براي کنترلر μ
شکل 44-16 پاسخ گذراي آشفته شده Y21 براي کنترلر μ
شکل 45-16پاسخ گذراي آشفته شده Y22 براي کنترلر μ
شکل 46-16 عمل کنترلي آشفته شده U11 براي کنترلر μ
شکل 47-16 عمل کنترلي آشفته شده U12 براي کنترلر μ
شکل48-16 عمل کنترلي آشفته شده U21 براي کنترلر μ
شکل 49-16 کنش کنترلي مختل شده U22 براي کنترلر μ
شکل 50-16 پاسخ هاي فرکانسي کنترلر مرتبه کامل و کاهش مرتبه يافته
7-16 شبيه سازي سيستم غير خطي
کنترلر μ طراحي شده بوسيله شبيه سازي سيستم حلقه بسته غيرخطي وابسته بررسي ميشود.
شبيه سازي بوسيله مدل سيمولينک nls_col.m انجام ميشود که مدل سيستم غيرخطي داده شده در بخش 2-16 را اجرا مي کند.
براي شبيه سازي سيستم غيرخطي با مجوز نويسنده، Skogested ، ام فايل هاي colamod و colas را بکار ميبريم.
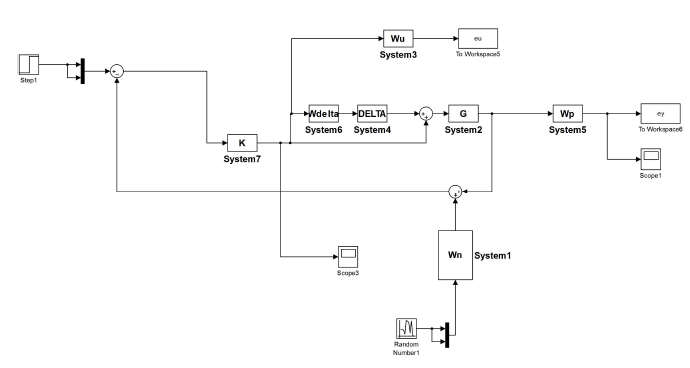
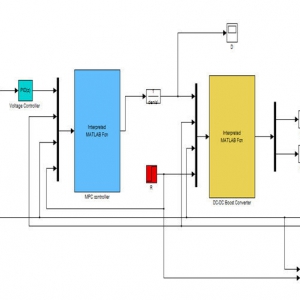
مدل سيمولينک سيستم کنترل ستون تقطير نشان داده شده در شکل 51-16 به ما اجازه ميدهد که شماري از شبيه سازي ها را براي اغتشاشات نقاط تنظيم// مختلف انجام دهيم.
توجه کنيد که ورودي ها به کنترلر بصورت اختلاف بين مقادير متغير هاي مربوطه و مقادير اسمي آنها (حالت پايا) که در خطي سازي بکار برده شده فرم دهي ميشود.
در مقابل ، به منظور بدست آوردن ورودي هاي کامل به مدل غير خطي ستون، خروجي هاي کنترلر به ورودي هاي اسمي وابسته اضافه ميشوند.
قبل از شبيه سازي سيستم، لازم است که پارامترهاي مدل را به وسيله بکاربردن ام فايل init_col.m تنظيم کنيد. همچنين کنترلر به سبب اجراي متغيرهاي ورودي/خروجي مقياس گذاري نشده، بازمقياس گذاري[41] ميشود.
شبيه سازي سيستم غيرخطي براي مرجع و سيگنالهاي اغتشاش زير انجام ميشود.
در t=10min نرخ خوراک F از 1 به 2/1 افزايش مييابد. در t=100min ترکيب خوراک ZF از 5/0 به 6/0 افزايش مييابد. در t=200min نقاط تنظيم در yD از 99/0 به 995/0 افزايش مييابد.
…..
شکل 51-16 مدل شبيه سازي سيستم غيرخطي
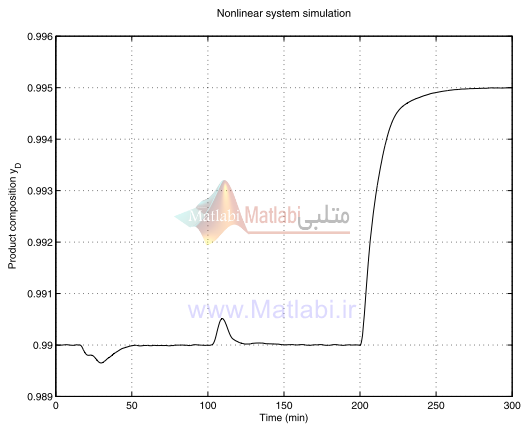
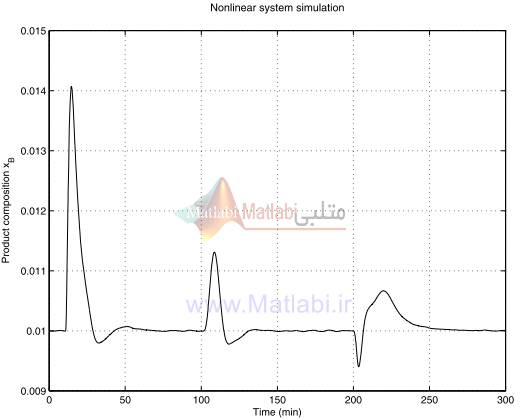
شکل 52-16 پاسخ گذراي سيستم غيرخطي YD
پاسخ زماني تقطير YD براي کنترلر μ کاهش مرتبه يافته در شکل 52-16 نشان داده شده است.
از شکل به نظر ميآيد که اغتشاشات به خوبي تضعيف ميشوند و نقاط تنظيم مورد نظر به طور دقيق حاصل ميشوند.
پاسخ زماني ترکيب محصول تحتاني XB براي همان کنترلر در شکل 53-16 نشان داده شده است.
نتايج شبيه سازي نشان ميدهد که روش طراحي مقاوم بطور مناسب انتخاب شده و اعتبار مدل نايقيني بکار برده شده را تاييد ميکند.
8-16. نتيجه گيري
نتايج آناليزها و طراحي سيستم کنترلي ستون تقطير ميتواند بصورت زير خلاصه سازي شود:
- اين امکان پذير است که يک مدل خطي سازي شده به اندازه کافي مرتبه پايين را براي سيستم غيرخطي داده شده بکار ببريم.
- بنابراين کنترلر خطي طراحي شده اجازه ميدهد که به ديناميک سيستم حلقه بسته غيرخطي قابل قبولي برسيم.
- مدل خطي شده به منظور اجتناب از سيگنالهاي خيلي بزرگ يا خيلي کوچک مقياس گذاري ميشود.
- دو کنترلر طراحي ميشود – يکي بوسيله بکاربردن روش طراحي شکل دهي حلقه يک درجه آزادي و ديگري بوسيله روش ترکيب μ دو درجه آزادي. هردو کنترلر خصوصيات حوزه زماني و فرکانسي را ارضا ميکنند و پايداري مقاوم سيستم حلقه بسته را تضمين ميکند.
- اين مهم است که چطور کنترلر شکل دهي حلقه طراحي شده مرتبه پايين به آساني به ما اجازه ميدهد که در عمل مشخصات يک سيستم حلقه بسته مثل کنترلر μ را بدست بياوريم. در حاليکه دومي به آزمايشات خيلي بيشتري براي تنظيم توابع وزني احتياج دارد.
شکل 53-16. پاسخ گذراي سيستم غيرخطي – xB
- نتايج شبيه سازي سيستم غيرخطي توانايي کنترلر را براي حصول تضعيف اغتشاشات و پاسخ خوب به سيگنالهاي مرجع تاييد ميکند.
- شبيه سازي اعتبار مدل نايقيني بکاربرده شده را تاييد ميکند.
9-16. مراجع و توجهات
مساله کنترل ستون تقطير بيان شده در اين بخش بوسيله ]97[ بصورت مساله محک //در کنفرانس کنترل و تعميم (داوري) 1991 معرفي شد. در ]97[ نايقيني مشخص ميشود.
ترم هاي نايقيني تاخيري و بهره پارامتري و اهداف کنترلي ترکيبي از خصوصيات حوزه فرکانسي و حوزه زمان هستند.
اين مساله گرفته شده ازSkogested ]97[ است جاييکه يک مدل ساده از ستون تقطير خلوص بالا بکار برده شد و خصوصيات عملکردي و نايقيني بصورت توابع وزني وابسته به فرکانس داده شد.
يک مقدمه آموزشي براي ديناميک ستون تقطير در ]154[ بيان شده است.
يک طراحي کنترلر شکل دهي حلقه دو درجه آزادي براي ستون تقطير در ]62[ بيان شده است، جاييکه يک مدل مرتبه 8 از ستون بکار برده ميشود.
در ]106[ يک کنترلردو درجه آزادي براي سيستم ستون تقطير با يک مدل مرجع و با استفاده از سنتز μ پيشنهاد ميشود.
در اين مقاله، يک روش انتخاب توابع وزن دهي که با جزييات توصيف شده، ميتواند يافت شود. طراحي ما با طراحي در ]106[ از چندين نظر متفاوت است. اولا بجاي مدل مرتبه دوم با تاخير زماني، يک مدل مرتبه 1 بکار برديم که بوسيله نتايج شبيه سازي سيستم غيرخطي تصديق ميشود.
دوما ما به منظور رسيدن به نتايج بهتر، توابع وزن دهي اصلاح شده را بکاربرديم به ويژه ما يک ماتريس تابع تبديل وزن دهي عملکرد با المان هاي غير صفر خارج از قطر اصلي را بکاربرديم که خصوصيات حوزه زمان را خيلي بهتر ملاقات ميکنند.
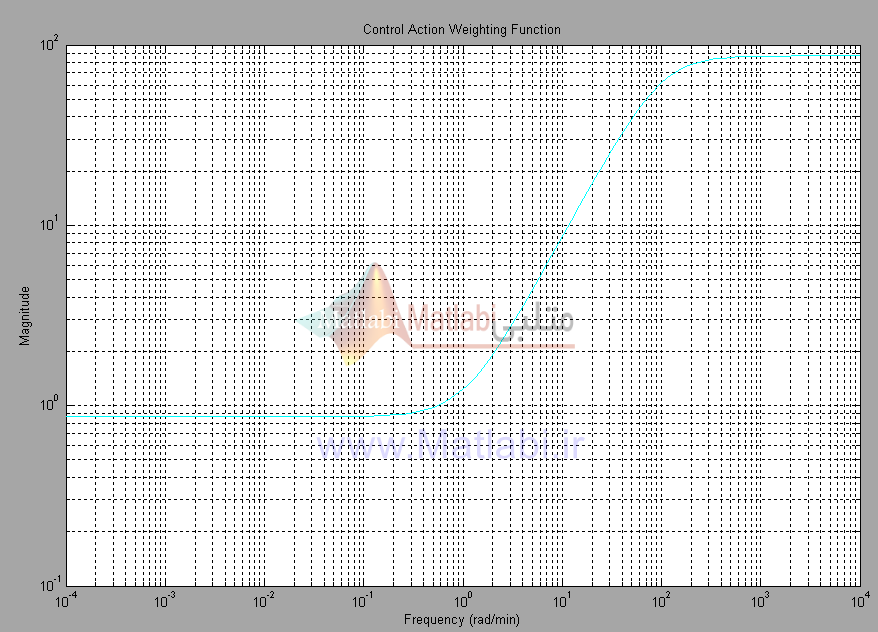
همچنين توابع وزن دهي کنترل بصورت فيلترهاي پايين گذر مرتبه اول در نظر گرفته ميشوند.
براي مقابله با مشکل ستون تقطير، علاوه بر روش هاي بالا، روش هاي طراحي متنوعي گزارش شده است ] 178,160,155,139,126[. در]178[ مساله طراحي بصورت يک مساله بهينه سازي ترکيب شده فرموله ميشود.
اين به خوبي شناخته شده است که مسايل طراحي سيستم کنترل ميتواند بصورت مسايل بهينه سازي تعبيه شده فرموله شود.
مشخصات طراحي در هر دو حوزه فرکانس و زمان و همچنين پايداري ميتواند بطور طبيعي بصورت قيود فرموله شود.
روشهاي بهينه سازي عددي ميتواند بطور مستقيم بکاربرده شود و يک راه حل بدست آمده (اگر وجود داشته باشد)يک طراحي قابل قبول را مشخص خواهد کرد.
بهرحال مسائل بهينهسازي معمولا به جهت دارا بودن قيود زياد، غير خطيها و نايقينيهاي زياد پيچيده ميباشند و در بيشتر موارد چندهدفه[42] با چندين هدف طراحي متناقض هستند که بايد بطور همزمان ارضا شوند.
بنابراين پارامتري کردن مستقيم کنترلر، پيچيدگي مساله بهينهسازي را افزايش خواهد داد. در ]178[ روش طراحي شکلدهي حلقه دنبال ميشود.
بجاي پارامتري کردن مستقيم کنترلرها، توابع وزندهي قبل و بعد سيستم افزوده (بکاربرده شده براي شکلدهي حلقه باز) بعنوان پارامترهاي طراحي (بهينهسازي) انتخاب ميشود.
ساختار ساده و مرتبه پاييني مانند توابع وزندهي موجب ميشوندکه بهينهسازي عددي بسيار موثرتر انجام شود.
نيازمنديها و اقتضائات نرم همچنين بر تنظيم قيد/هزينه مشتمل است.
پايداري سيستم حلقه بسته بطور طبيعي بوسيله کنترلرهاي طراحي شده اين چنيني ملاقات ميشود. طراحيهاي رضايتبخشي در آن مقاله گزارش ميشوند. مرجع ]160[ روش بهينهسازي در ]178[ را با بکارگيري يک الگوريتم ژنتيک براي انتخاب پارامترهاي تابع وزندهي بطور مفصل بسط ميدهد.
کنترل خطي مربعي گوسي ستون تقطير
در اين پروژه در نظر داريم، يک سيستم چند ورودي- چند خروجي ستون تقطير را با استفاده از روش LQG/LTR،کنترل کنيم.
پس از بيان خلاصه اي از روش LQG/LTRنتايج حاصل از اعمال اين روش ذکر گرديده است. در انتها جمع بندي روش بيان گرديده است.
روش LQG
ميخواهيم کنترلکنندهاي با استفاده از معيار LQGطراحي کنيم. در واقع ميخواهيم بهترين طراحي فيدبک حالت و رويتگر حالت را همزمان داشته باشيم. لذا به دنبال فيلتر کالمنو مسئلة طراحي رگولاتور بهينه ميرويم. براي شروع طراحي دو راه پيش رو داريم.
- بهرة فيلتر() را طوري طراحي کنيم تا رفتار مناسبي داشته باشد، سپس بهرة کنترلکننده() را بگونهاي بدست آوريم که به سمت ميل کند، که به اين روش بازيابي حلقهميگويند.
- بهرة کنترلکننده را طوري طراحي کنيم تارفتار مناسبي داشته باشد و پس از آن بهرة فيلتر را طوري تغيير دهيم تابه سمت ميل کند.
حل مساله LQG يعني تخمين حالتها به کمک تخمين زننده بهينه فيلتر کالمن و طراحي رگولاتور بهينه خواهد بود.
دراينجا تنها نتايج اين روش را بيان مي کنيم. همانطور که مي دانيم، هم رگولاتور LQ و هم فيلتر کالمن علمکرد و مقاوم بودن خوبي دارند، بنابراين انتظار مي رود کنترل کننده LQG هم خواص خوبي داشته باشد. ولي در حالت کلي اينگونه نيست.
در واقع دو روش براي طراحي LQG داريم.
يا بهره فيدبک را قبل از طراحي فيلتر کالمن طراحي مي کنيم يا ابتدا يک فيلتر مي سازيم و بعد بهره فيدبک را ايجاد مي کنيم. اگر دو روش مختلف از طراحي LQG را به کار بريم به دو نوع راه حل متفاوت مي رسيم.
به منظور پايدار سازي و رسيدن به عملکرد مطلوب يک راه انتخاب مقادير ويژه فيلتر کالمن در محل صفرهاي سيستم مي باشد.
در اين روش امکان شکل دهي بهره هاي اساسي نرخ بازگشت در خروجي يا ورودي سيستم به طراح داده مي شود تا به اين وسيله بتوان به مشخصات عملکردي مطلوب و مقاوم بودن مناسب دست پيدا کرد. از مزاياي اين روش اين است که ذاتا پايدار ميباشد.
بنابراين نگران مشخصه هاي فاز نخواهيم بود.
دراين روش ابتدا با طراحي يک فيلتر کالمن و سپس رگولاتور بهينه در قالب مسأله LQG به شرايط مطلوب کنترلي دست پيدا مي کنيم.
سپس بااستفاده از تکنيک LTR حلقه را در خروجي بازيابي مي کنيم. بلوک دياگرام زير ساختار LQG با دو محل بازيابي حلقه را نشان ميدهد.
شکل 14: ساختار جبرانساز LQG با دو محل بازيابي حلقه
تئوري روش طراحي LQG/LTR
کنترلکننده LQG از دو قسمت تشکيل شدهاست:
1. فيلتر کالمن: تخمينگر بهينه براي تخمين زدن حالتهاي سيستم که همان فيلتر کالمن است.
منظور از طراحي فيلتر کالمن در واقع يافتن بهره تخمينگر بهينه يا بگونهاي است که کوواريانس خطاي ميان حالت و تخمين آن کمينه گردد.
براي اين کار از تابع Kalman در نرمافزار Matlab استفاده ميکنيم.
وروديهاي اين تابع سيستم اوليه و واريانس نويز و خروجي سيستم است و خروجي آن بهره تخمينگر يا و واريانس خطاي تخمين است.
2. رگولاتور بهينه(LQR): در اين قسمت هدف طراحي يک رگولاتور بهينه براي انجام کنترل است.
در واقع اين رگولاتور بمنظور ايجاد يک قانون کنترل بهينه با هدف کاهش اندازه ورودي و حالات سيستم بکارگرفته ميشود.
در واقع منظور از طراحي رگولاتور بهينه يافتن بهره بگونهاي است که يک تابع هزينه مشخص کمينه گردد.
براي اين کار از تکنيک LTR براي بازيابي مشخصات عملکردي خوب براي سيستم استفاده ميشود.
منظور از مشخصات مطلوب حدفاز 60 درجه و حدبهره بينهايت است.
تکنيک LTR شامل يافتن بهره براساس تنظيم وزنهاي تابع هزينه کنترل کننده LQR و برخي مشخصات مربوط به مدل نويز است تا جاييکه مشخصات پايداري سيستم قبل از اضافه شدن رگولاتور بهينه مجدداً بازيابي شود.
مسئله LQG وطراحي فيلتر کالمن
فرض مي کنيم مدل سيستم به صورت زير داده شده باشد:
…
که در آنها w,v به ترتيب نويز اندازه گيري و نويز فرآيند فرض مي شوند. هدف يافتن قانون کنترلي است که تابع هزينه زير را کمينه کند.
…
که درآن z=Mx مي باشد.
براي حل اين مساله ابتدا حالتها رابه کمک فيلتر کالمن تخمين مي زنيم. بهره فيلتر کالمن مناسب از حل يک معادله ريکاتي به صورت زير به دست مي آيد. نهايتاً با استفاده از حالتهاي تخمين زده شده بهره فيدبک حالت مناسب را نيز از حل يک مساله رگولاتور بهنيه محاسبه مي کنيم.
تابع تبديل کنترل کننده LQG
بازيابي بهرة حلقه
سيستمي با معادلات حالت زير را در نظر بگيريد.
در بازيابي بهرة حلقه بايد به نکاتزير توجه داشت:
- بايستي اکيداً سرهباشد، و اگر سره بود، مجبوريم يک قطب دور نسبت به ديگر قطبهاي آن، اضافه نمائيم تا اکيداً سره گردد.
- همچنينپايداريپذير وآشکاريپذير باشند.
فرض ميکنيم، جبرانساز مورد استفاده به ترتيب زير باشد.
ميخواهيم، را بگونهاي بيابيم که حلقة کنترل شکل(15) عملکرد مطلوبي داشته باشد.
شکل(15)- حلقة کنترلي در بازيابي بهره
با در نظر گرفتن نقاط 1 و 2 ميتوان دو بهرة حلقة متفاوت داشت، که به ترتيب بهرة حلقه در ورودي کنترلکننده و بهرة حلقه در خروجي کنترلکننده مشهور ميباشند.
حال اگر بتوان را طوري انتخاب کرد که رفتار مطلوب گردد،را ميتوان به گونهاي انتخاب کرد که :
و يا اگر بتوانرا طوري انتخاب کرد که رفتار مطلوب گردد،را ميتوان به گونهاي انتخاب کرد که :
در اين تحقيق ما بازيابي بهرة حلقه در خروجي را پيگيري ميکنيم. به ترتيبي که را بهرة فيلتر کالمن در نظر ميگيريم. اکنون بايد ببينيم که چگونه ميتوان بهرة کنترلکننده() را بدست آوريم که داشته باشيم:
براي اين منظور مسئلة LQR زير را در نظر ميگيريم:
که در آن،
اکنون اگرورا طوري انتخاب کنيم که بتوانرا از رابطة ريکاتي بدست آورد، مسئله حل شده است.
با بدست آوردن از معادلة فوق داريم:
با توجه به مزايايي که بازيابي حلقه درخروجي در طراحي مشخصات تابع حساسيت براي طراح به همراه دارد، از اين روش استفاده مي کنيم. به عبارت ديگر مساله طراحي با روش LQG/LTR در دو گام زير خلاصه مي شود:
- طراحي يک فيلتر کالمن همانطور که قبلا هم ذکر شد با دستکاري ماتريسهاي کواريانس W,V به منظور دستيابي به يک نرخ بازگشت مطلوب درخروجي سيستم.
- افزودن يک رگولاتور فيدبک حالت بهينه با قراردادن
و افزايش q(يا کاهش ) تا خروجي سيستم جبران شده در يک محدوده نسبتاً وسيع فرکانسي به شکلي مناسب به همگرا شود.
البته بايد توجه داشت که کاهش بيش از حد (با توجه به نسبت عکس راديکال با پهناي باند) سبب افزايش حساسيت به نويز و نامعينيهاي فرکانس بالا خواهد شد.
شکل دهي بهره هاي اساسي
همانطور که ديديم بايستي به نحوي ماتريسهاي V,W را براي رسيدن به تغييرات دلخواه بدانيم. در اين راستا دو راه حل عمده وجود دارد:
- اصلاح ماتريسهاي V و
- اصلاح مدل فرآيند با افزودن ديناميکهاي اضافي
براي اصلاح ماتريسهاي و V معمولاً سعي مي شود تا بهره هاي اساسي در حوالي فرکانس گذر از 0dB به هم شبيه شوند.
در بسياري موارد اصلاح ماتريسهاي و V به تنهايي کافي نيست.
در اينگونه موارد مدل فرآيند با افزودن ديناميکهاي اضافي اصلاح مي شود. از مهمترين مواردي که در آن از مدل فرآيند اصلاح شده استفاده مي شود، زماني است که هدف دستيابي به حساسيت صفر در فرکانس است.
دراين گونه موارد يک انتگرالگير به سيستم اضافه مي شود.
البته با توجه به اينکه قراردادن قطبي درمبدا بازيابي حلقه را با مشکل مواجه مي سازد، معمولاً اصلاح مدل فرآيند در مبدا قرار نميدهند وآن را بسيار نزديک به مبدا انتخاب مي کنند.
معمولاً اصلاح مدل فرآيند ابتداي طراحي انجام مي گيرد و سپس شکل دهي بهره هاي اساسي براي مدل اصلاح شده انجام ميپذيرد.
اعمال روش LQG/LTR بر روي سيستم
مرحله اول طراحي فيلتر کالمن مي باشد. طراحي اين قسمت شامل يافتن يک بهره KF است که متناسب با آن خطاي خروجي از مقدار تخمين زده شده در تخين حالت تاثير داده مي شود بطوريکه کوواريانس خطاي حالت از مقدار تخمين زده شده حداقل گردد.
از تابع Kalman در نرم افزار MATALB استفاده مي کنيم که سيستم اوليه و واريانس نويزهاي موثر در حالات و خروجي سيستم را بعنوان ورودي دريافت کرده و بهره Kf و کوواريانس خطاي تخمين حالت را بعنوان خروجي توليد مي نمايد.
اين مرحله با شکل دهي بهره هاي اساسي نرخ بازگشت صورت ميگيرد.
از اين رو بهره هاي اساسي حالت حلقه باز سيستم را با استفاده از دستور Sigma رسم مي کنيم.
همانطور که از شکل هم مشخص است، بهره هاي اساسي در اين حالت ضمن اينکه داراي دامنه کم هستند، اختلاف زيادي نيز باهم دارند، براي طراحي بايستي ضمن بهبود پهناي باند و دامنه، بايستي اين بهره هاي اساسي به هم نزديک شوند.
از سوي ديگر با توجه به شيب dB0 درفرکانسهاي پايين بايستي يک انتگرال گير به سيستم اضافه کرد تا به شيب dB/dec20- برسيم.
در اين مرحله ميخواهيم بهره فيلتر کالمن را طراحي کنيم. در اينجا براي واريانس نويز اندازهگيري و نويز حالت ماتريس واحد را در نظر ميگيريم. شکل (16) نمايش بهرههاي اساسي سيستم حلقه باز است.
شکل(16): بهرههاي اساسي سيستم حلقه باز
شکل(17) نمايش بهرههاي اساسي فيلتر کالمن يعني پس از اولين طراحي براي بهره است.
همانطورکه مشاهده ميشود بهرههاي اساسي سيستم در فرکانسهاي پايين مقادير بسيار کوچکي دارند.
بدين ترتيب لزوم وجود يک انتگرلگير کاملا احساس ميشود. براي بهبود طراحي يک انتگرالگير ار در فرکانسهاي پايين به سيستم اضافه ميکنيم.
در اين مرحله با تقويت مدل فرايند يک انتگرلگير به سيستم اضافه ميکنيم. از آنجاييکه اضافه کردن انتگرالگير در فرکانس صفر در مرحله LTR مشکل ايجاد ميکند، انتگرالگير در فرکانس بسيار پايين که نزديک به صفر باشد مثلاً 001/0 هرتز به سيستم اضافه ميشود.
شکل (18) نمايش بهرههاي اساسي سيستم فيلتر کالمن پس از اضافه کردن انتگرالگير را نشان ميدهد. ديده ميشود که با افزايش انتگرلگير ميزان بهرهها در فرکانسهاي پايين بوضوح افزايش يافته است.
همچنين بدليل قرار نگرفتن قطب انتگرالگير در مبدا شيب بهرههاي اساسي در فرکانسهاي پايين نهايتا صفر شده و بهره dc بينهايت نخواهد شد.
شکل(17): بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf1
شکل(18): بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf2
حال به منظور افزايش سرعت کاهش خطاي حالت ماندگار بايد کوچکترين بهره اساسي (PG) را افزايش دهيم به گونهاي که اندازه آن در فرکانس پايين تقريبا برابر با اندازه بزرگتريت PG گردد.
براي اين کار بايد کوچکترين بهره را در فرکانس پايين افزايش دهيم.
شکل (19) نشان ميدهد که بهره جديد فيلتر کالمن اين خواسته را برآورده کرده است.
شکل(19): بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf3
در گام چهارم طراحي فيلتر کالمن، توجه خود را به تغيير پهناي باند سيستم معطوف ميکنيم. براي رسيدن به پهناي باند مطلوب بايد بهرههاي اساسي را کاهش داد.
با تغيير ضريب ماتريس W و محاسبه بهرههاي جديد بر اساس بهره کالمن Kf4 نمودار بهرههاي اساسي به شکل (20) در ميآيد.
شکل(20): بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf4
به منظور بررسي بيشتر و دستيابي به بهترين عملکرد براي فيلتر کالمن در ادامه به بررسي بهرههاي اساسي توابع حساسيت و متمم حساسيت (تابع تبديل حلقه بسته) فيلتر کالمن ميپردازيم. در شکل (12) اين بهرهها رسم شده است.
با توجه به اينکه در حوالي فرکانس گذر از 0 dB بهرهها يکسان هستند، لذا طراحي توسط فيلتر کالمن در اين قسمت خاتمه پيدا کرده و بهره نهايي فيلتر کالمن که همان Kf4 است را در ادامه طراحي لحاظ ميکنيم. در ادامه به فاز دوم طراحي يعني بازيابي حلقه خواهيم پرداخت.
شکل(21) : بهرههاي اساسي تابع حساسيت و تابع تبديل حلقه بسته فيلتر کالمن با استفاده از بهره Kf4
شکل(22): بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهرهKf5
شکل(23) : بهرههاي اساسي تابع حساسيت و تابع تبديل حلقه بسته فيلتر کالمن با استفاده از بهره Kf5
بازيابي حلقه درمدل
پس از طراحي فيلتر کالمن براي تخمين حالات سيستم، نوبت به طراحي يک رگولاتور مناسب براي سيستم ميشود. جبرانسازهاي LQG عموماً عملکرد و مقاومت خوبي دارند. براي طراحي يک رگولاتور بايدضرايب تابع هزينه را تا دستيابي به عملکرد مورد نظر تغيير دهيم. براي طراحي رگولاتور مناسب دو روش بکاربرده ميشود.
قرار دادن و و کاهش بهره را با حل مساله LQR چنان تعيين مينماييم تا بهره حلقه در خروجي سيستم يعني به بهره در رنج نسبتاً وسيعي از فرکانسها منطبق گردد. لازم به ذکر است که بهره فيلتر کالمن Kf همان Kf4 است که در گام قبل محاسبه شد و به صورت زير است.
شکل(24) نمايش بهرههاي اساسي به ازاي مقادير مختلف ميباشد. همانطور که ديده ميشود به ازاي عملکرد سيستم بسيار مناسب است.
مشاهده ميکنيم که با کاهش مقداربهرة کنترلکننده افزايش مييابد و بازيابي بهتري انجام ميشود به طوري که بهرههاي اساسي کاملاً بر هم منطبق مي شوند.از نقطه نظر ديگر ميتوان گفت که هرچه کاهش يابد، افزايش مييابد و سيگنال کنترلي قويتري در خلاف جهتحرکت حالتهاي سيستم ايجاد ميشوند و تأثير کنترلکننده افزايش مي يابد.
شکل(24): بازيابي بهرههاي اساسي حلقه باز به ازاي مقادير مختلف
در نهايت کنترل کننده نهايي بر اساس بهره فيلتر کالمن و بهره رگولاتور بصورت زير در ميآيد.
شکل (25) پاسخ پله سيستم حلقه بسته را با توجه به طراحي انجام شده براي بهره تخمينگر حالت(فيلتر کالمن) و رگولاتور بهينه با بستن حلقه فيدبک، نشان ميدهد.
شکل(25): پاسخ پله حلقه بسته سيستم كنترل پس از بازيابي حلقه و اعمال فيدبك
همانگونه که ديده ميشود پاسخ حلقه بسته بسيار مطلوب بوده و خطاي ماندگار کاملاً از بين رفته و اندرکنش بين وروديها و خروجيهاي نامتناظر تاحدود زيادي رفع شده است.
کاهش پيچيدگي کنترل کننده با محدود کردن ساختار کنترل کننده
در کنترل مقاوم معمولا ابعاد کنترل کننده بدست آمده براي مقابله با نامعيني از مرتبه بالا بدست مي آيد. حال مي خواهيم براي رفع اين مشکل ساختار کنترل کننده را محدود مي کنيم مثلا کنترل کننده را PIDدرنظر ميگيريم و سپس پارامترهاي کنترل کننده را به نحوي مي يابيم که کنترل کننده معيارهاي قوام و عملکرد سيستم را ارضا کند.
براي اين کار با استفاده از ابزار بهينه سازي هوشمند به جستجوي پارامترهاي بهينه کنترل کننده PID براي کاهش کران بالاي تابع خروجي( کنترلH-Infinity) وکاهش واريانس سيگنال کنترل به همراه خطاي کنترلي مي باشيم( کنترل H2) اما پس از چندين روز شبيه سازي مساله با استفاده از الگوريتم هاي تکاملي تجمع ذرات و تطبيق ماتريس کوواريانس به نتيجه مطلوب و پايدار نرسيديم.
حال سوال اينجاست آيا اين روش هاي بهينه سازي قادر به حل مساله نمي باشند و يا از لحاظ ساختاري کنترل کننده PID جوابگوي اين مساله نيست. سوال بعدي اين است که اگر اين کنترل کننده جوابگوي مساله نباشد راه بهبود و حل مساله چيست؟
در حال حاضر به پاسخ متقني براي جواب اين مساله نيافتيم.
شکل(26) : ساختار شبيه سازي simulink با استفاده از الگوريتم هوشمند
سيستم غير خطي اوليه شامل يك سري معادله ديفرانسيل مرتبه 82 و غير خطي مي باشد كه داراي خاصيت ناهمواري حل [43] مي باشند.
پس از خطي سازي حول نقطه تعادل مورد نظر كه مشخصات آن در[1] ارائه شده است، مدل مرتبه 82 خطي سازي شده حاصل مي شود. اين مدل كماكان پيچيده مي باشد و براي سادگي بيشتر تحت الگوريتم كاهش مرتبه بالانس شده، مرتبه آن تا مرتبه 6 كاهش مي يابد.
تابع تبديل سيستم حلقه باز پس از كاهش مرتبه از سيستم اوليه ، به فرم زير مي باشد. تابع تبديل G به صورت زير مي باشد[13]. توابع وزني از نتايج حاصل از مرجع[1] اخذ شده است.
قطب هاي اين سيستم همگي پايدار مي باشند. با اين حال سيستم چند متغييره داراي يك جفت صفر انتقال غير كمينه فاز مي باشد.
اما اين صفرها از مبدا بسيار فاصله دارند و از اين رو اثر غير كمينه فازي آنها اندك است. نمودار زير صفرها و قطبهاي مدل كاهش مرتبه يافته را نشان مي دهد.
با استفاده از جعبه ابزار کنترل مقاوم در حوزه فرکانس که توسط آقاي دکتر کريمي و همکارانش در دانشگاه EPFL سوييس تهيه شده به طراحي کنترل کننده مقاوم براي ستون تقطير مي پردازيم.
اين بسته نرم افزاري ابزاري براي طراحي کنترلرهاي پارامتري خطي مقاوم در حوزه نايکوييست است. در اين رويکرد کنترل کننده هاي مقاوم بر مبناي معيار H infinity يا حاشيه هاي قوام کلاسيک مثل حاشيه بهره و فاز براي يک يا چند سيستم SISO يا MIMO مي تواند به کار رود.
در تمامي اين موارد مسايل بهينه سازي خطي يا محدب حل ميگردد. براي حل مسايل بهينه سازي خطي يا مربعي از دستور Linprog يا Quadprog نرم افزار MATLAB استفاده مي کند.
مسايل بهينه سازي محدب با نرم افزار YALMIPفرموله شده و با تمامي حل کننده هاي موجود( به صورت پيش فرض Sdpt3) حل مي شوند.
شکل دهي حلقه با کنترل کننده مقاوم PID
در روش شکل دهي حلقه اختلاف بين تابع تبديل حلقه باز L و تابع تبديل مطلوب حلقه باز(Ld) در بازه فرکانسي در نظر گرفته شده مينيمم مي گردد.
تابع تبديل مطلوب حلقه باز(Ld) بايد تعداد قطب هاي ماپايدارش باتعداد قطب هاي ناپايدار مدل برابر باشد تا شرايط معيار نايکوييست برقرار گردد. کران پايين براي حاشيه مدول(معکوس نرم بينهايت تابع حساسيت)تضمين شده است.
براي دوحالت حاشيه مدول 0.9 و 1.1 ضرايب کنترل کننده PID با فيلتر مشتقي را جستجو مي کنيم.
K1 =
From input 1 to output…
0.00016533 (s+1.685e05) (s+4.187)
1: ———————————
s (s+8333)
-0.00071068 (s+3.198e05) (s-0.5068)
2: ———————————–
s (s+8333)
From input 2 to output…
-9.9526e-05 (s-1.199e05) (s-7.676)
1: ———————————-
s (s+8333)
0.00015853 (s-6.649e05) (s+0.8823)
2: ———————————-
s (s+8333)
K2 =
From input 1 to output…
6.0293 (s-0.54) (s+7.042)
1: ————————-
s (s+8333)
-5.4475 (s+0.09145) (s+47.66)
2: —————————–
s (s+8333)
From input 2 to output…
0.21888 (s+7.676) (s-16.78)
1: —————————
s (s+8333)
-3.1557 (s+0.09951) (s+92.54)
2: —————————–
s (s+8333)
هر چه حاشيه مدول را بزرگتر در نظر بگيريم امکان يافتن کنترل کننده کمتر شده و سيستم رفتار گذراي نامطلوبي از خود نشان مي دهد
شکل(27): مقادير استثنايي تابع حساسيت در دو حالت
شکل(28): مقادير استثنايي تابع مکمل حساسيت در دو حالت
شکل(29): پاسخ پله تابع مکمل حساسيت در دو حالت
شکل(30): پاسخ پله تابع حساسيت در دو حالت
شکل(31): پاسخ منحني بد تابع حساسيت و مکمل حساسيت
شکل دهي حلقه با کنترل H infinity
در روش شکل دهي حلقه با کنترل H infinityاختلاف بين تابع تبديل حلقه باز L و تابع تبديل مطلوب حلقه باز(Ld) در بازه فرکانسي در نظر گرفته شده تحت قيود H infinity بر روي توابع وزن دار حلقه بسته مينيمم مي گردد.
در اين قسمت مي خواهيم با کنترل کننده مورد نظر نرم بي نهايت اختلاف توابع وزن دار حلقه بسته(نرم وزن دار تابع حساسيت و مکمل حساسيت) و تابع تبديل مطلوب را مينيمم نماييم.
ساختار کنترل کننده متشکل از ساختار متمرکز دو در دو مي باشد.
در واقع چهار کنترل کننده خواهيم داشت. هر يک ازکنترل کننده هاي تعريف شده از ضرب 3 پارامتر کنترلي در توابع تبديل زير بدست مي آيد.
در جعبه ابزار امکان تعريف کنترل کننده با ساختار از پيش تعريف شده وجود دارد. تابع M مدل مرجع مطلوب مد نظر است. با داشتن آن مي توان تابع تبديل حلقه مطلوب را محاسبه کرد.
M=1/(s*(s+2))
Ld=M/(1-M)
phi = conphi(‘ud’,[1 ; 1/s ; s/(sˆ2+2*s+1)]);
From input to output…
1: 1
1
2: –
s
s
3: ————-
s^2 + 2 s + 1
پس از محاسبه با استفاده از جعبه ابزار ياد شده، کنترل کننده به صورت زير بدست مي آيد.
K =
From input 1 to output…
0.08802 s^3 – 1.085 s^2 + 0.1871 s + 0.04954
1: ——————————————–
s^3 + 2 s^2 + s
-0.08203 s^3 – 1.444 s^2 + 0.01682 s + 0.04943
2: ———————————————-
s^3 + 2 s^2 + s
From input 2 to output…
0.002978 s^3 – 0.7468 s^2 – 0.09599 s – 0.04949
1: ———————————————–
s^3 + 2 s^2 + s
-0.05331 s^3 – 0.2965 s^2 – 0.1613 s – 0.05398
2: ———————————————-
s^3 + 2 s^2 + s
شکل(32): مقادير استثنايي تابع حساسيت و مکمل حساسيت
شکل(33): پاسخ پله تابع حساسيت و مکمل حساسيت
شکل(34): پاسخ منحني بد تابع حساسيت و مکمل حساسيت
قسمت سوم: ديكوپلينگ ديناميكي:
پيکربندي ها و ماتريس بهره[44]
از نقطه نظر کنترلي، يک برج تقطير دو محصولي با خوراک معين، 5 درجه آزادي دارد. در حالت ماندگار فرض فشار ثابت و کنترل سطح کامل[45] در چگالنده و گرم کننده، درجه آزادي را به 2 کاهش مي دهد.
اين دو درجه ازادي مي توانند براي کنترل غلظت دو محصول استفاده شوند.
اثر تغييرات کوچک دو درجه آزادي باقيمانده، مي تواند با خطي سازي مدل بدست آيد. مثلاً در پيکربندي ، و بعنوان درجه هاي آزادي (متغيرهاي مستقل) در نظر گرفته مي شوند و در حالت ماندگار مي توان نوشت :
بطوريکه اثر تغيير کوچک در روي با ثابت نشان مي دهد. در شکل ماتريسي داريم:
بطور مشابه ، در پيکربندي ، و بعنوان درجه هاي آزادي (متغيرهاي مستقل) در نظر گرفته مي شوند و در حالت ماندگار مي توان نوشت :
در حقيقت بينهايت ترکيب از 5 جريان اصلي مي توانند بعنوان متغيرهاي اصلي در نظر گرفته شوند و بطور خاص نسبت بين اين متغيرها مي توانند بعنوان متغيرهاي مستقل بکارگرفته شوند. پيکربندي و نمونه اي از اين نوع پيکربندي ها است که در حالت ماندگار مي توان نوشت :
ويژگي هاي کنترلي پيکربندي هاي مختلف، مي تواند به شکل قابل ملاحظه اي متفاوت باشد و اين مسئله با مطالعه تداخل دوطرفه حالت ماندگار[46] که بصورت آرايه بهره نسبي(RGA) [47] بيان مي شود نشان داده خواهد شد. بهره نسبي اين را بيان مي کند که در واقع بهره چگونه نغيير مي کند هنگاميکه ديگر حلقه ها بسته مي شود.
طبق تعريف ماتريس RGA برابر است با :
بطوريکه :
بطور کلي ترجيح مي دهيم که ورودي و خروجي را بگونه اي جفت کنيم که المان هاي روي قطر اصلي ماتريس RGA نزديک يک باشد. براي هر يک از پيکربندي هاي معرفي شده مقدار تقريبي براي بهره نسبي از روابط زير بدست مي آيد :
همانطور که قابل مشاهده است المان هاي ماتريس RGA براي پيکربندي همواره براي جداسازي هاي با خلوص بالا داراري مقدار بزرگي است. از طرف ديگر، براي در پيکربندي ، المان هاي RGA همواره بين يک و صفر هستند. براي پيکربندي و ، RGAنسبت به پيکربندي هنگاميکه جريان هاي داخلي بالا هستند کاهش مي يابد.
در اين قسمت W1GW2 مدل خواهد شد كه در آن W2=I و W1=G-1 در نظر گرفته خواهد شد. با استفاده از معكوس G مي توان در برخي از سيستمها، كوپلينگ وودي و خروجي از بين برد و يك ساختار قطري ديكوپل شده را مورد بررسي و كنترل قرار داد.
در ابتدا با توجه به مرتبه دوم بودن ساختار Wها، يك كاهش مرتبه دوم اعمال مي گردد و پس از آن بحث پيش فيلتر و پس فيلتر افزوده خواهد شد.
در اين مثال W1 به صورت روبرو در نظر گرفته مي شود:
Num=[1.0000 0.3120 0.0016]
Den=[1 -0.4282 0.2711 0.1716]
پس از اعمال W1 ، كنترلر به صورت ذيل در خواهد آمد:
…
حال اگر l(s) به صورت l(s)=k/S انتخاب شود خواهيم داشت:
…
پس از طراحي موارد مطروحه، تغييرات در نرم افزار متلب اعمال گرديد و نتايج ذيل حاصل گرديد:
همانطور كه در شكلها ديده مي شود در روش ديكوپلينگ در تمام بازه فركانسي پايداري مقاوم نداشته و در بعضي محدوده ها پايداري و نيز عملكرد مقاوم به خطر مي افتد.
Stability margin emax = 0.28
هنگاميكه گين را افزايش مي دهيم اين محدوده كمتر هم مي گردد مثلا با گين 10 اين محدوده به 0.15 مي رسد.
نتايج :
- 1- روش ديكوپلينگ گزينه مناسبي براي طراحي كنترلر در اين سيستم نمي باشد. دلايل آن عبارتند از:
- الف- براي تحليل سيستم ما مجبور به كاهش مرتبه شده بوديم و براي تعيين فيلتر جبرانساز مجبور به كاهش مرتبه دوباره شديم.
- ب- با توجه به اينكه تعداد خروجي از برج را دو محصول با دو خاصيت در نظر گرفته ايم، اما فاكتورهايي را كه كنترل مي نماييم چهار فاكتور هستند، در ضمن عدم استقلال فاكتورهاي ياد شده، روش ديكوپلينگ را بي تاثير مي نمايد.
- Mixture ↑
- Component Fraction ↑
- Boiling Mixture ↑
- More Volatile Component ↑
- Manufacturing ↑
- Heating ↑
- Cooling ↑
- Operating Cost ↑
- Batch Column ↑
- Feed ↑
- Continuous Column ↑
- Throughput ↑
- Binary ↑
- Multi-Component ↑
- Extractive ↑
- Azeotropic ↑
- Vertical Shell ↑
- Column Internals ↑
- Trays ↑
- Reboiler ↑
- Condensor ↑
- Reflux Drum ↑
- Feed Tray ↑
- Top Section ↑
- Bottom Section ↑
- Rectification ↑
- Enriching ↑
- Stripping ↑
- Bottom Product ↑
- Top Product ↑
- Distillate ↑
- Flow ↑
- Mole Fraction ↑
- Boilup Flow ↑
- Theoretical Stages ↑
- Total Condenser ↑
- Bottom ↑
- Liquid Holdup ↑
- Relative Volatility ↑
- Settling time ↑
- rescaled ↑
- multiobjective ↑
- Non stiffness ↑
- Configuration and Gain Matrix ↑
- Perfect Level Control ↑
- Steady-State Two-Way Interaction ↑
- Relative Gain Array ↑
کلید واژه: H infinity, کنترل کننده مقاوم PID, LQG/LTR, LQG وطراحي فيلتر کالمن, کنترل خطي مربعي گوسي ستون تقطير,
شبیه سازی مقاله Robust Control of a Distillation Column
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.



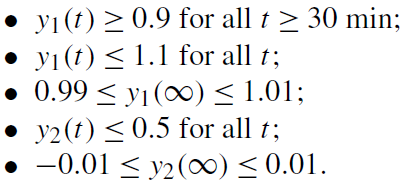
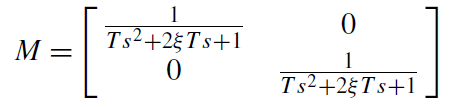







دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.