توضیحات
RNGA based control system configuration for multivariable processes
ترجمه فارسی موضوع مقاله: RNGA مبتنی بر پیکربندی سیستم کنترل برای فرآیندهای چندمتغیره
در زیر گزارش بدون آوردن معادلات قرار داده شده است:
قطبهای سیستم نیز عبارتند از:…
برای بدست آوردن صفرهای دکوپله ورودی و خروجی میتوان یک تحقق مینیمال(مثلا گیلبرت) برای تابع تبدیل مورد نظر نوشت و از روی آن صفرهای دکوپله ورودی و خروجی را بدست آورد.
یک فرم فضای حالت مینیمال برای تابع در نظر گرفته شده به صورت زیر است.
…
ماتریس سیستم رزنبراک به صورت زیر بدست میآید….
برای بدست آوردن صفرهای دکوپله از یکی از دو فرمول زیر استفاده میکنیم…
صفرهای دکوپله سیستم= صفرهای دکوپله ورودی (با حذف صفرهای دکوپله خروجی)- صفرهای دکوپله ورودی
صفرهای دکوپله سیستم= صفرهای دکوپله خروجی (با حذف صفردکپلهی خروجی)-صفرهای دکوپله خروجی
برای بدست آوردن صفرهای دکوپلهی ورودی توجه داریم چون تحقق مینیمال است پس کنترل پذیر و رویت پذیر است چون کنترل پذیر (رویت پذیر) است پس صفر دکوپلهی ورودی(خروجی) نداریم. و هرکدام از شرایط کنترل پذیری و رویت پذیری که برقرار باشد صفر دکوپله نخواهیم داشت.
ضمنا توجه داریم که صفر انتقالی سمت راست نداریم و نیازی به جایابی صفر انتقال نمیباشد.
برای دکوپله سازی بوسیلهی فیدبک حالت ابتدا باید ببینیم این سیستم قابلیت دکوپلهسازی بوسیلهی فیدبک حالت را دارد یا خیر.
ابتدا ماتریس D که که درجهی نسبی سطر وستون است را بدست میآوریم.
…
برای اینکه سیستم را بتوانیم دکوپله کنیم باید دترمینان ماتریس زیر مخالف صفر باشد
با توجه به اینکه دترمینان ماتریس دکوپله سازی () مخالف صفر است پس دکوپله سازی قابل انجام است.
روش دیگر بدست آوردن به این صورت است که…
که در آن و سطرهای اول و دوم ماتریس c هستند و و دو عدد هستند که به ازای آنها و مخالف صفر هستند.
که در این سیستم خواهد بود.
همانطور که دیده میشود این با بدست آمده از روش قبل یکی است و دترمینان آن نیز مخالف صفر است که نشان میدهد دکوپله سازی قابل انجام است.
برای بدست آوردن ماتریس داریم …
سیگنال کنترل فیدبک حالت دکوپله ساز بایستی به فرم زیر ساخته شود.
و ماتریس تابع تبدیل سیستم دکوپله شده به صورت زیر خواهد.
و سیستم حلقه بسته به صورت زیر میشود.
با جایگذاری عددی خواهیم داشت.
…
برای تحلیل پایداری به روشهای مختلفی میتوان عمل کرد یکی از این روشها نایکویست است.
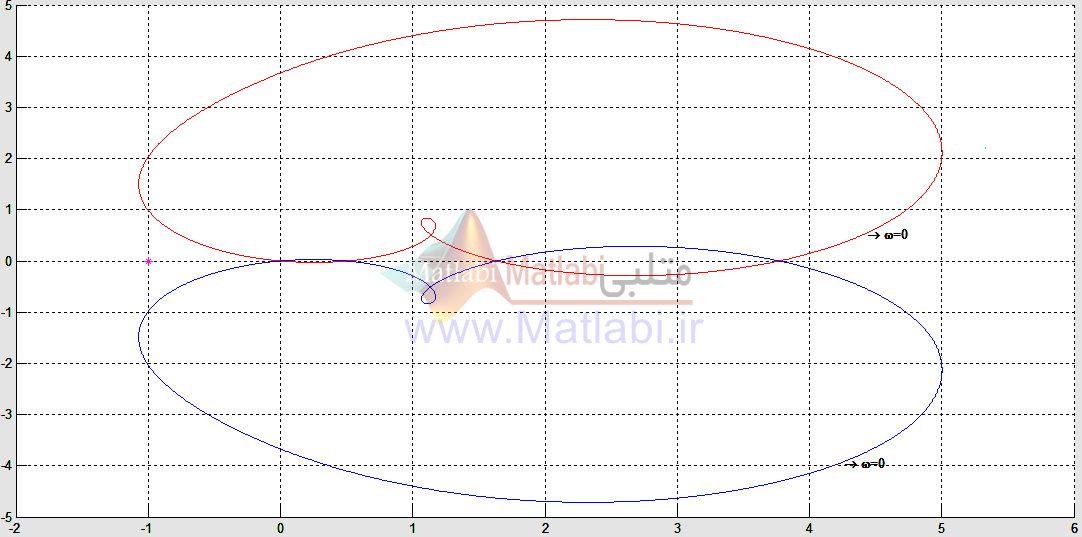
برای تحلیل از روش نایکویست ابتدا بایستی دیاگرام نایکویست تابع مورد نظر را ترسیم کنیم و داریم.
سیستم قطب سمت راستی ندارد.
: دو بار دور می زندو ناپایدار است
: دور نمی زند و پایدار است
دو بار دور می زندو ناپایدار است
: دور نمی زند و پایدار است
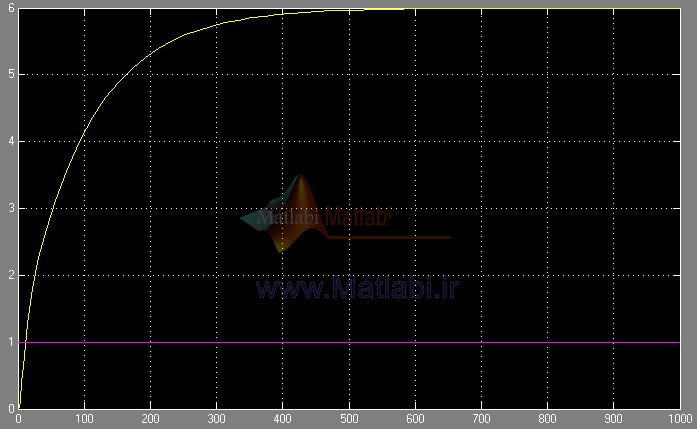
پاسخ پله سیستم به ازای در زیر ترسیم شده است.
خروجی اول
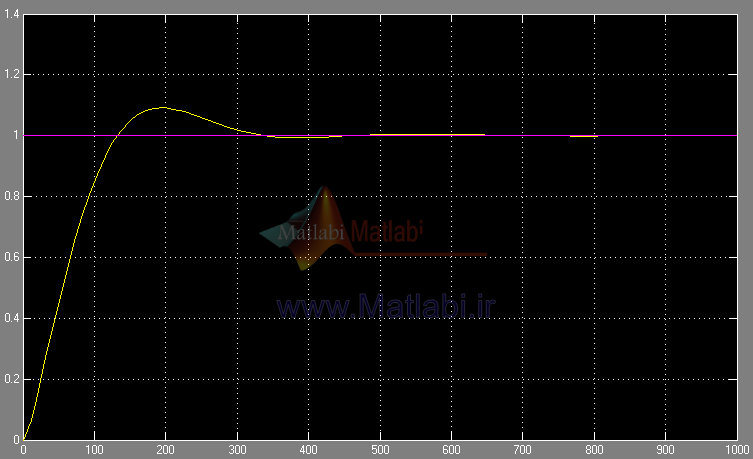
خروجی دوم:
برای انتخاب پیکربندی مناسب برای کنترل سیستم یکی از بهترین معیارها یا همان ماتریس آرایه بهرهی نسبی است.
با توجه به ماتریس آرایهی بهره نسبی بدست آمده مناسب است که کنترل خروجی اول با ورودی اول کنترل خروجی دوم با ورودی دوم انجام پذیرد. و ضمن اینکه اگر خروجی اول را ورودی اول کنترل کنیم تداخل کمتری در سیستم خواهیم داشت.
برای طراحی کنترل کننده میتوان کنترل کننده را به فرم در نظر گرفت. این کنترل کننده را برای افزایش سرعت پاسخ گذرای سیستم را به صورت تناسبی در نظر گرفته ایم.
البته توجه داریم که با توجه به اینکه
رابطهی به فرم زیر خواهد بود
با انتخاب سیستم فوق هم حذف اغتشاش دارد و هم ردیابی خروجی مورد نظر به خوبی انجام میدهد.
با توجه به اینکه در طراحی کنترلر به روش ترتیبی ترم تداخلی را به صورت اغتشاش میبینیم کافیست برای
کنترلری pi طراحی شود که داریم.
به ازای این ضرائب کنترلر هم دفع اغتشاش خوبی دارد و هم پاسخ پلهی مناسبی.
برای خروجی دوم هم با دیدن ترم تداخلی به صورت اغتشاش خواهیم داشت.
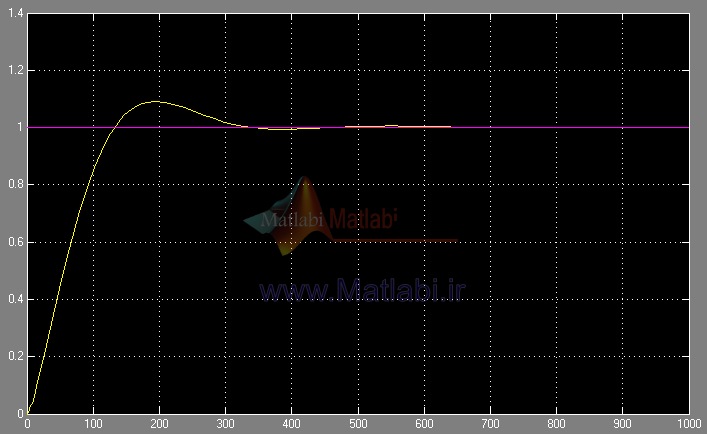
با ورودی [ 0 1] پاسخ و به ترتیب به صورت زیر خواهند بود.
با ورودی [ 1 0] پاسخ و به ترتیب به صورت زیر خواهند بود.
همانطور که از شکلها پیداست تداخل کانال اول روی دوم بیشتر از کانال دوم روی اول است و این موضوع را از روی ماتریس بهرهی آرایه نسبی هم قابل فهمیدن بود.
کلید واژه :
کنترل چند متغیره، MIMO
Multivariable processes, Decentralized control, Interaction measurement, Loop pairing, Relative gain array, Niederlinski index, Relative normalized gain array, Controller independent, Simulation
شبیه سازی RNGA based control system configuration for multivariable processes
با توضیحات فوق تهیه شده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.








دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.