توضیحات
Performance of three recursive algorithms for fast space-variant Gaussian filtering
ترجمه فارسی موضوع مقاله: بررسی عملکرد الگوریتمهای بازگشتی برای فیلتر گوسی سریع متغیر با مکان
1) مقدمه
فیلتر گوسی نقش مهمی در بسیاری از روشهای استخراج ویژگی و مدلسازی بیولوژیک دارد.
از جمله این کاربردها میتوان به مدلسازی عملکرد فویا در شبکیه چشم اشاره کرد.
بدین صورت که پیادهسازی عملکرد آن معادل فیلتر کردن تصویر با استفاده از هسته گوسی و نمونهبرداری غیریکنواخت تصویر است.
مشکل اصلی در این قسمت هزینه محاسباتی بالای عملگر کانولوشن تصویر است.
این هزینه بالا مخصوصاً در کاربردهای زمان-حقیقی بسیار نامناسب است.
یکی از راههای مناسب کاهش هزینه محاسباتی، تقریب بازگشتی فیلتر گوسی است.
دلایل اصلی این تقریب عبارتست از:
1- میزان دقت بالای روش
2- تعداد کم عملیات برای هر پیکسل
3- تعداد عملیات هر پیکسل ثابت است و بسته به مقیاس ندارد.
4- میزان سادگی ترکیب گوسی با هر مقیاس.
الگوریتمهای بازگشتی گوسی به سه تکنیک کلی تقسیم میشود.
1- تقریب دریشه[1] تابع گوسی در حوزه مکان
2- تقریب جین[2] در حوزه
3- تقریب ولیت[3] در حوزه فوریه
کارهای انجام شده در این مقاله به دو دسته کلی تقسیم میشود:
1- توسعه الگوریتمهای بیان شده بازگشتی گوسی به حالت متغیر با مکان. ضرایب این فیلتر با تغیر در حوزه مکان تصویر تغییر میکنند.
2- ارزیابی و مقایسه عملکرد سه تکنیک بازگشتی. این مقایسه با فیلتر گوسی حقیقی انجام میشود.
2) فیلتر بازگشتی
هدف از فیلتر گوسی بازگشتی، تقریب در حوزه تابع گوسی با نسبت دو چندجملهای به همدیگر است.
فیلتر گوسی به شکل زیر بیان میشود:
…
این عمل یعنی تقریب به صورت کسر چندجملهای منجر به کاهش قسمت کانولوشن و هزینه محاسباتی میشود.
روابط مربوط به سه تکنیک بیان شده در قسمت قبل برای تقریب بازگشتی گوسی در مقاله ذکر شده است.
این روابط با سه تابع با نامهای Derichefcn ، Jinfcn و Vlietfcn پیادهسازی شدهاند.
ضرایب چندجملهای صورت کسر نشان دهنده کانولوشن و ضرایب مخرج کسر نشان دهنده بازگشت است.
رابطه مذکور را در حوزه مکان میتوان به صورت زیر نوشت:
…
3) گسترش به حالت متغیر با مکان
فیلترهای پیاده شده در قسمت قبل مربوط به سیگنالهای یکبعدی بودند.
در این قسمت ابتدا گسترش این فیلترها به حالت دوبعدی انجام میشود که این کار به دلیل جداپذیری سیگنال گوسی به راحتی انجام میشود.
علاوه بر این حالت متغیر با مکان برای تقریب گوسی درنظر گرفته میشود.
یعنی این فیلتر برای پیکسلهای مختلف تصویر دارای ضرایب متفاوتی میباشد.
معادله این فیلتر در حوزه مکان به شکل زیر میباشد:
…
ضرایب فیلتر یعنی و توابعی از هستند.
4) روشهای ارزیابی و مقایسه
سه روش کلی برای مقایسه عملکرد توابع تقریبی گوسی بازگشتی با تابع گوسی حقیقی درنظرگرفته شده است:
…
1- پاسخ ضربه فیلترها محاسبه شده، با تابع گوسی حقیقی مقایسه میگردد.
این مقایسه هم به صورت کیفی با مشاهده خروجی فیلترهای یکبعدی و دوبعدی و هم به صورت کمی انجام میشود.
معیارکمی بکار رفته برای مقایسه عبارتست از:
…
در این رابطه پاسخ ضربه فیلتر گوسی بازگشتی تقریبی و پاسخ ضربه فیلتر گوسی واقعی است.
تعداد نقاط موجود در حوزه یعنی نقاط با فاصله کمتر از از مرکز گوسی است.
2- خروجی فیلترها و فیلتر گوسی حقیقی برای یک تصویر نمونه مقایسه شده است.
همه تصویر با یک مقیاس یکسان فیلتر میشود. انجام پروژه متلب با متلبی
تصویر نمونه بکار رفته یک آرایه از نویزهای تصادفی یکنواخت است.
معیار کمی بکاررفته برای مقایسه روشها در این قسمت همان خطای rms نرمالیزه است که به صورت زیر محاسبه میشود:
…
در این رابطه تصویر خروجی بدست آمده از اعمال فیلتر گوسی بازگشتی تقریبی و تصویر خروجی پاسخ ضربه فیلتر گوسی واقعی است.
تعداد کل پیکسلهای تصویر است.
3- همه فیلترها در حوزه متغیر با مکان آزموده میشوند.
میزان در مرکز تصویر برابر 1 و در گوشهها برابر 4 است.
روابط بکار رفته برای تابع به دو صورت خطی (رابطه 6) و سینوسی (رابطه 7) است.
…
در این روابط فاصله بین مرکز و هرکدام از گوشههای تصویر است.
در انتها نیز سرعت فیلترها یعنی میزان هزینه محاسباتی پیادهسازی آنها مورد بررسی قرار میگیرد.
5) نتایج و بحث
در این بخش نتایج حاصل از پیادهسازی سه فیلتر نشان داده میشود و با مقایسه نتایج آنها با نتایج حاصل از اعمال فیلتر گوسی واقعی ارزیابی از عملکرد سه روش خواهیم داشت.
برنامه اصلی MATLAB نوشته شده برنامه Main است که در آن نتایج اصلی ارائه شده در مقاله پیادهسازی شده و بدست آمده است.
در این راستا برای پیادهسازی سه فیلتر از روابط اصلی موجود در بخش 2 مقاله و ضمیمه A و B استفاده شده است.
 |
| شکل 1. پاسخ ضربه یک بعدی فیلتر Deriche. تابع گوسی واقعی به شکل دایره نشان داده شدهاند. |
 |
| شکل 2. پاسخ ضربه یک بعدی فیلتر Jin. تابع گوسی واقعی به شکل الماس نشان داده شدهاند. |
 |
| شکل 3. پاسخ ضربه یک بعدی فیلتر Vliet. تابع گوسی واقعی به شکل الماس نشان داده شدهاند. |
 |
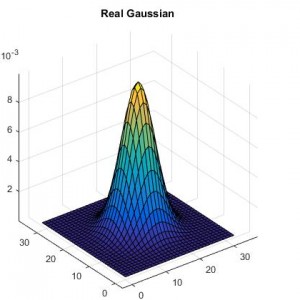
| شکل 4. نمای سهبعدی و سطح مقطع پاسخ ضربه دوبعدی سه فیلتر Deriche (ستون چپ)، Jin (ستون وسط) و Vliet (ستون راست). |
 |
| شکل 5. تصویر نمونه اولین و خروجی حاصل از اعمال فیلتر متغیر با مکان با نگاشت مقیاس سینوسی |
کلید واژه : پردازش تصویر,فیلتر بازگشتی, فیلتر گوسی
شبیه سازی مقاله Performance of three recursive algorithms for fast space-variant Gaussian filtering
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.