توضیحات
Parametric convergence and control of chaotic system using adaptive feedback linearization
توجه نمایید در اینجا برخی از معادلات یا تصاویر نیامده است.
در فایلهایی که خریداری می نمایید هیچگونه نام یا واترمارکی از سایت متلبی وجود ندارد.
چکیده
روش خطی سازی فیدبک، روشی برای طراحی یک کنترل کننده غیر خطی است.
در مورد این روش تحقیقات بسیار زیادی صورت گرفته است و این روش کنترلی دارای کاربرد های عملی زیادی از جمله بالگرد ها،ربات های صنعتی و فضاپیما ها می باشد.
ایده اصلی این روش حذف اثر غیر خطی یک سیستم غیر خطی از طریق تبدیلات جبری می باشد که از این طریق مدل دینامیکی غیر خطی سیستم به یک مدل خطی تبدیل می شود و سپس از طریق تکنیک های خطی تحلیل پایداری یا ردیابی صورت می گیرد.
روش خطی سازی فیدبک دارای دو ساختار متفاوت می باشد.
خطی سازی ورودی-حالت و خطی سازی ورودی-خروجی.
در این پروژه هر دو ساختار مورد تحلیل و بررسی قرار گرفته اند.
این گزارش از پنج قسمت تشکیل شده است.
بخش اول مقدمه ای کوتاه در مورد روند کلی این گزارش می باشد.
در بخش دوم روش خطی سازی فیدبک به طور مختصر اشاره شده است.
در بخش سوم سیستم های مورد استفاده در این پروژه معرفی شده است.
در بخش چهارم شبیه سازی این روش کنترلی و نتایج آن ارائه شده است.
در انتها نیز نتیجه گیری کلی از این رویکرد کنترلی صورت گرفته است.
بخش اول
مقدمه
روش خطی سازی فیدبک با انجام یک دسته تبدیلات جبری مدل دینامیک غیر خطی سیستم را به طور کلی یا جزئی به مدل دینامیک خطی تبدیل می کند و سپس از ابزار های کنترل خطی برای پایدارسازی و یا مسئله ردیابی استفاده می کند.
در واقع این روش با اعمال یک قانون کنترلی غیر خطی مناسب ابتدا اثر غیر خطی سیستم را حذف می کند و سپس با اعمال یک قانون کنترل خطی مانند جایگذاری قطب اهداف کنترلی مسئله را برآورده می کند.
انتخاب این قوانین کنترلی از طریق یک دسته تبدیلات جبری صورت می گیرد.
ساختار این روش را می توان به دو دسته تقسیم کرد.
خطی سازی ورودی – حالت (Input-State Linearization)
خطی سازی ورودی – خروجی (Input-Output Linearization)
جزئیات این دو روش در بخش بعد اشاره خواهد شد.
در این گزارش ابتدا با استفاده از مدل دینامیکی یک سیستم غیر خطی آشوب گونه روش خطی سازی ورودی – حالت مورد تحلیل قرار گرقته شده است که تمرکز اصلی ما بر روی این سیستم است.
اما برای تحلیل روش خطی سازی ورودی-خروجی دو نمونه سیستم غیر خطی اشاره شده در کتاب Slotine مورد استفاده قرار گرفته شده اند و نتایج شبیه سازی آن نشان ارائه شده است.
این گزارش را می توان به پنج بخش اساسی تقسیم کرد.
بخش اول مقدمه ای کوتاه در مورد روند کلی این پروژه می باشد.
بخش دوم که به تحلیل مختصر در مورد روش خطی سازی فیدبک و انواع آن می پردازد.
در بخش سوم سیستم های غیر خطی مورد استفاده در این پروژه معرفی می شوند.
در بخش چهارم شبیه سازی سیستم کنترلی طراحی شده به همراه تحلیل های لازم و نتایج شبیه سازی در مورد هر دو نوع روش خطی سازی فیدبک ارائه می شود.
بخش پنجم هم نتیجه گیری کلی از این رویکرد کنترلی می باشد.
انجام پروژه متلب با سایت متلبی , خطی سازی و هر نوع پروژه کنترلی را به متخصصین سایت متلبی بسپارید.
بخش دوم
خطی سازی فیدبک Feedback Linearization ) )
مقدمه
روش خطی سازی فیدبک ،روشی برای طراحی یک کنترل کننده غیر خطی است به گونه ای که این کنترل کننده اثرات غیر خطی سیستم غیر خطی را حذف می کند و با تبدیل دینامیک غیر خطی سیستم به یک مدل دینامیکی خطی (تبدیل کامل یا جزئی) از تکنیک های کنترل خطی برای پایدارسازی یا ردیابی مسیر مطلوب استفاده می کند.
همانطور که اشاره شد این روش یک رویکرد پرکاربرد در زمینه های عملی چون بالگرد ها ،فضاپیما های با عملکرد بالا ، مواد زیست شناسی پزشکی و ربات های صنعتی می باشد.
این روش به طور کلی به دو نوع اساسی تقسیم می شود.
روش خطی سازی ورودی – حالت و روش خطی سازی ورودی – خروجی.
روش خطی سازی ورودی – حالت
در روش خطی سازی ورودی – حالت سیستم های غیر خطی به فرم کلی زیر می باشند.
در واقع این روش از دو مرحله اساسی تشکیل شده است.
در مرحله اول با استفاده از تبدیل
و یک قانون کنترلی غیر خطی مناسب به صورت
اثر غیر خطی سیستم حذف می شود و مدل دینامیکی غیر خطی سیستم به یک مدل دینامیکی خطی به فرم
تبدیل می شود.
سپس با اعمال یک قانون کنترل v پایداری دینامیک خود سیستم یا دینامیک خطای سیستم تضمین می شود.
به طور معمول در مسئله خطی سازی ورودی – خروجی بحث پایداری داخلی و کنترل حالت های سیستم در شرایط اولیه خاصی مورد بررسی قرار می گیرد.
اما می توان از این روش برای مسئله ردیابی هم استفاده کرد.
البته معادله حرکت مطلوب باید بر اساس متغیر های جدیدی که برای تبدیل جبری لازم است به دست آید.
بلوک دیاگرام این روش کنترلی به صورت زیر می باشد.
همانطور که در بالا مشاهده می شود این سیستم کنترلی از دو حلقه داخلی و خارجی تشکیل شده است.
حلقه داخلی عمل خطی سازی دینامیک سیستم را بر عهده دارد و حلقه خارجی کار پایدارسازی سیستم غیر خطی را بر عهده دارد.
در این روش به طور معمول با توجه به نحوه انتخاب قانون کنترل غیر خطی برای خطی سازی دینامیک غیر خطی سیستم ،قانون کنترل دارای نقطه یا نقاط تکینی می باشد که این مسئله حوزه پایداری سیستم را تحت الشعاع خود قرار می دهد.
از طرفی برای پیاده سازی این رویکرد کنترلی نیاز به اندازه گیری همه حالت ها می باشد زیرا به طور معمول حالت های جدید تعریف شده و قانون کنترلی غیر خطی به تمام حالت های سیستم وابسته می باشند.
نکته اساسی در مورد این روش این است که به طور کلی روش خطی سازی فیدبک به شدت وابسته به مدل سیستم است.
بنابراین برای پیاده سازی این روش از یک طرف باید سیستم را باید به خوبی شناخت.
از طرف دیگر اگر نامعینی در مدل یا پارامتر های سیستم رخ دهد این نامعینی یا عدم قطعیت روی عملکرد سیستم کنترلی تاثیر گذاشته و باعث تضعیف عملکرد آن می شود.
بنابراین این روش ،یک روش کنترلی مقاوم نیست.
روش خطی سازی ورودی – خروجی
این روش کنترلی به طور معمول در مورد سیستم هایی به فرم زیر به کار می رود.
هدف کنترلی ما در اینجا به طور معمول ردیابی یک مسیر مطلوب می باشد.
ایده اساسی این روش این است که بتوان به طریقی ارتباط خطی و صریحی بین ورودی کنترل و خروجی تعریف شده برای سیستم پیدا کرد و سپس با اعمال یک قانون کنترل مناسب دینامیک سیستم را خطی کرد و سپس هدف ردیابی را برآورده کرد.
برای این منظور از خروجی تعریف شده برای سیستم تا زمانی که این ارتباط خطی و صریح بین ورودی و خروجی دیده شود مشتق گرفته می شود.
در نتیجه با توجه مرتبه مشتق خروجی درجه نسبی برای سیستم تعریف می شود.
از طرفی اگر درجه نسبی سیستم از مرتبه خود سیستم کمتر باشد.
بحث دینامیک داخلی پیش می آید.
در اینجا فقط اشاره می کنیم که اگر ما به هر طریقی توانستیم مدل دینامیکی خطی شده سیستم را پایدار کنیم هنوز کار تمام نشده است و باید پایداری دینامیک پنهان یا همان دینامیک داخلی سیستم را نیز بررسی کنیم.
زیرا این روش کنترلی در صورتی تضمین پایداری سیستم را می کند که دینامیک داخلی سیستم پایدار باشد.
برای بررسی پایداری دینامیک داخلی از مفهومی به نام پایداری صفر سیستم که یک ویژگی داخلی سیستم است استفاده می شود.
در این روش فرض بر این است که مشتقات خروجی تعریف شده و مسیر مطلوب معلوم بوده و کراندار می باشند.
همچنین قانون کنترلی مورد استفاده نیز ممکن است دارای نقطه یا نقاط تکین باشد.
در این روش نیز نیاز به اندازه گیری تمام حالت ها می باشد.
نکته مهم در اینجا این است که در این روش اگر درجه نسبی سیستم با مرتبه سیستم برابر باشد روش خطی سازی ورودی – خروجی به روش خطی سازی ورودی – حالت تبدیل می شود.
بخش سوم
معرفی سیستم
مقدمه
در این بخش به معرفی سیستم های مورد استفاده در این پروژه برای روش خطی سازی فیدبک می پردازیم.
لازم به ذکر است که برای تحلیل هر دو نوع روش کنترلی از چند مدل استفاده شده است.
سیستم اصلی مورد استفاده در این پروژه یک سیستم آشوب گونه است که از یک مقاله گرفته شده است.
چندین دهه می باشد که سیستم های آشوب و رفتار آنها مورد تحلیل و بررسی قرار گرفته شده اند.
این سیستم ها حساسیت زیادی به شرایط اولیه دارند که همین امر عملکرد فرایند های فیزیکی را محدود می کند.
از آنجایی که به طور معمول پیش بینی رفتار آشوب یک سیستم مشکل است ،این آشوب باعث ناپایداری سیستم و به طور معمول باعث تضعیف عملکرد یک سیستم می شود.
به همین دلیل باید این رفتار از مشخصه رفتاری یک سیستم حذف شود.
کنترل رفتار آشوب از این جهت که باعث نوسانات نامنظم می شود ضروری است زیرا این پدیده برای وسیله های فیزیکی نامطلوب است.
این نوسانات نامنظم به طور معمول باعث صدمه زدن به ابزار های فیزیکی می شود.
کنترل رفتار آشوب در زمینه هایی چون مبدل های dc-dc ،تنظیم دینامیک سیال،طراحی سیستم ها به منظور ارتباطات امن و بعضی مسائل مرتبط با علم زیست پزشکی کاربرد دارد.
سیستم آشوب Genesio-Tesi
سیستم آشوب Genesio-Tesi با مجموعه معادلات دیفرانسیل به صورت زیر ارائه می شود.
در معادلات بالا x1,x2,x3 حالت های سیستم هستند.
a,b,c ثابت های حقیقی مثبت هستند که شرط ab<c را برآورده می کنند.
a,b,c پارامتر های خطی و d پارامتر غیر خطی این سیستم آشوب می باشد.
بدون اینکه کلیت مسئله از بین برود مقدار d را یک در نظر می گیریم.
ثابت k نیز یک عدد اسکالر است که فرض بر این است که معلوم است.
u ورودی اعمالی به سیستم می باشد.
برای اینکه نشان دهیم این سیستم دارای رفتار آشوب است پارامتر های a,b,c را مطابق مقاله به ترتیب 1.92 ، 2.92 و 6 در نظر می گیریم و ثابت های k,d را 1 در نظر می گیریم.
با انتخاب شرایط اولیه مطابق مقاله به صورت
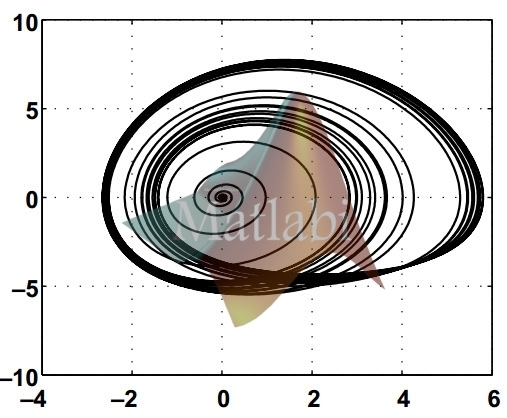
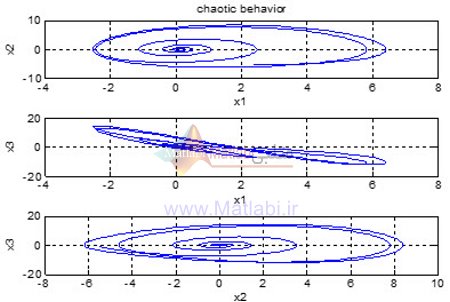
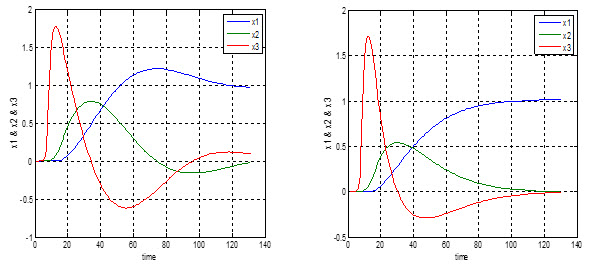
شکل پرتره فازی سیستم مورد نظر ما به صورت زیر خواهد شد.
شکل های بالا رفتار آشوب این سیستم را تحت شرایط اولیه ذکر شده نشان می دهند.
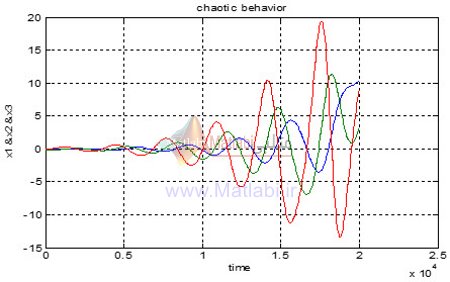
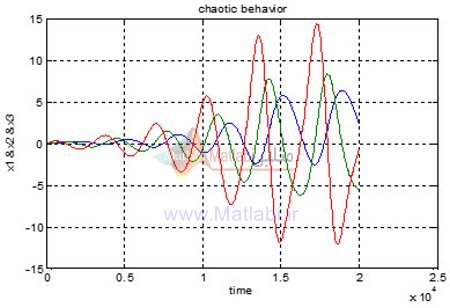
رفتار حالت های سیستم در مقیاس زمانی به صورت زیر می باشد.
همانطور که از شکل بالا مشخص است حالت ها در حالت ورودی صفر و تحت وجود شرایط اولیه دارای رفتار نوسانی نا منظم می باشند که از مشخصه های آشوب می باشد.
حال همین رفتار آشوب را تحت اعمال یک ورودی پله بررسی می کنیم.
1) ورودی پله با وجود شرایط اولیه بالا
2) ورودی پله در حالت سکون
رفتار حالت های سیستم در مقیاس زمانی
در بخش بعد کنترل رفتار آشوب این سیستم غیر خطی را از طریق روش خطی سازی ورودی – حالت نشان خواهیم داد.
انواع دیگر سیستم ها
در مورد همین روش خطی سازی ورودی – حالت یک نمونه سیستم دیگر که از کتاب Slotine گرفته شده است نیز اجرا شده است.
معادلات این سیستم به صورت زیر می باشد.
روش خطی سازی ورودی – خروجی نیز در اینجا تحلیل شده است.
برای این منظور از دو نمونه سیستم اشاره شده در کتاب Slotine استفاده شده است که در این بخش فقط معادلات آن را نشان می دهیم.
سیستم اول به صورت زیر می باشد.
سیستم دیگری که برای نوع دوم خطی سازی مورد استفاده قرار گرفته شده است دارای معادلاتی به فرم زیر می باشد.
در بخش بعدی چگونگی استفاده از روش خطی سازی فیدبک در قالب هر دو نوع آن به همراه شبیه سازی سیستم ها و نتایج این شبیه سازی ها ارائه خواهد شد.
بخش چهارم
تحلیل روش خطی سازی برای سیستم های مورد نظر به همراه شبیه سازی
خطی سازی ورودی – حالت
در روش ورودی حالت با انتخاب متغیر های جدید یا به عبارت دیگر با تبدیل حالت ابتدا معادله دینامیکی غیر خطی سیستم را به فرم کانوکیکال خطی در می آوریم.
البته از یک قانون کنترل غیر خطی نیز در این زمینه استفاده می کنیم.
سپس از روش جایگذاری قطب سیستم مورد نظر را کنترل می کنیم.
فرم کلی معادلات یک سیستم غیر خطی را به صورت زیر در نظر بگیریم.
جایی که f وg توابع برداری به صورت زیر می باشند.
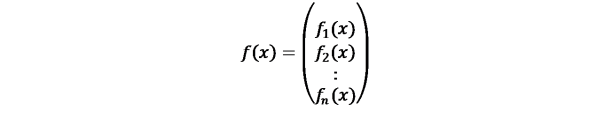
روند کلی این روش بر اساس یک دسته عبارت های جبری به صورت زیر می باشد.
- ابتدا از روی معادلات حالت سیستم دو مجموعه عبارت های زیر را تشکیل می دهیم.
در این مرحله باید استقلال خطی عضو های مجموعه A و شرط Involoutivity برای اعضای مجموعه B را بررسی کنیم.
این کار به خاطر این است که دو شرط مذکور وجود تبدیل حالت مناسب برای خطی سازی سیستم غیر خطی را اثبات می کنند یعنی اگر شرط های بالا برآورده نشوند تبدیل حالتی وجود نداشته و نمی توان از روش خطی سازی ورودی – حالت برای کنترل یک سیستم غیر خطی استفاده کرد.
2) بعد از اطمینان از وجود یک تبدیل حالت مناسب متغیر های جدید را از روابط زیر به دست می آوریم.
در نتیجه متغیر های جدید به صورت زیر به دست می آیند.
…
4) اگر قانون کنترل غیر خطی جهت خطی سازی را به صورت
در نظر بگیریم.با انجام مراحل بالا این قانون کنترل به صورت زیر در خواهد آمد.
قانون کنترل بالا سیستم غیر خطی را خطی خواهد کرد و قانون کنترل خطی v کار پایدارسازی سیستم را بر عهده دارد.
این قانون خطی به صورت زیر می باشد.
خطی سازی ورودی – خروجی
در روش خطی سازی ورودی – خروجی باید از خروجی تعریف شده برای سیستم مشتق بگیریم تا جایی که ارتباط خطی و صریحی بین ورودی و خروجی پیدا شود.
روند کلی این روش را می توان به مراحل زیر تقسیم کرد.
1) تعیین درجه نسبی سیستم از روی مرتبه مشتق خروجی
2) تعیین قانون کنترلی به طوری که معادله مشتق خروجی به صورت زیر در آید.
جایی که r درجه نسبی سیستم می باشد.
3) قانون کنترلی مناسب برای رسیدن به معادله بالا به صورت زیر می باشد.
4) تعیین v به صورتی که دینامیک خطای سیستم به سمت صفر همگرا شود.
این قانون کنترل به صورت زیر می باشد.
برای تضمین پایداری دینامیک خطا ضرایب k0 تا kn را باید به گونه ای به دست آورد که معادله
تمام ریشه هایش سمت چپ محور موهومی باشد.
تحلیل سیستم ها
روش خطی سازی ورودی – حالت
1) سیستم آشوب Genesio-Tesi
همانطور که اشاره شد تمرکز اصلی ما در این پروژه بر روی سیستم آشوب Genesio-tesi به فرم معادلات زیر می باشد.
در این قسمت ابتدا به طور تحلیلی و سیستماتیک روش خطی سازی ورودی – حالت را روی این سیستم مطابق مراحلی که در بالا اشاره شد اعمال می کنیم و سعی می کنیم تا با این روش رفتار آشوب سیستم را کنترل کنیم.
مطابق روند کلی روش ورودی – حالت ابتدا باید مجموعه های A و B را به دست بیاوریم.
بنابراین ابتدا باید را به دست آوریم.
لازم به ذکر است که پارامتر های خطی و غیر خطی مسئله را بدون از دست دادن کلیت مسئله به صورت زیر در نظر گرفته ایم.
حال مجموعه های A و B را تشکیل می دهیم.
…
برای مجموعه A باید شرط استقلال خطی اعضای آن و برای مجموعه B باید شرط involoutivity را بررسی کرد.
برای بررسی استقلال خطی اعضای مجموعه A را به صورت ترکیب خطی زیر می نویسیم.
حال با عملیات سطری خواهیم داشت:
بنابراین شرط استقلال پذیری برآورده می شود.حال شرط involoutivity را بررسی می کنیم.
برای این کار باید رابطه زیر بین برقرار باشد.
…
بنابراین شرط involoutivity نیز برقرار است.
حال می دانیم که تبدیل حالت لازم جهت به دست آوردن قانون کنترل وجود دارد.
در این مرحله این تبدیل حالت را می یابیم.
برای این منظور از روابط زیر استفاده می کنیم.
در نتیجه خواهیم داشت:
…
بنابراین با توجه به روابط بالا متغیر حالت اول به دست می آید.
از طرفی روابط بالا به گونه ای است که رابطه متغیر های بعدی با قبلی به صورت زیر می باشد.
بنابراین متغیر های جدید عبارتند از:
حال با توجه به اینکه
قانون کنترل مناسب به صورت زیر خواهد شد:
در نتیجه از روابط بالا خواهیم داشت:
حال معادلات جدید سیستم را می نویسیم.
بنابراین برای پایداری سیستم کافی است v را به صورت
انتخاب کنیم.
در نتیجه نوع پاسخ سیستم در این شرایط به پارامتر های k1,k2,k3 بستگی پیدا می کند.
در قسمت بعد سیستم آشوب مورد نظرمان را شبیه سازی می کنیم.
شبیه سازی سیستم Genesio-Tesi
همانطور که مشاهده کردیم قانون کنترل مناسب جهت اهداف کنترلی موردنظرمان در قسمت قبل به روش تحلیلی به دست آمد.
در این قسمت نتایج به دست آمده را از طریق محیط سیمولینک MATLAB شبیه سازی کرده و نتایج را ارائه می دهیم.
در ابتدا سیستم اولیه بدون اجرای روش خطی سازی ورودی – حالت شبیه سازی شده است.
نمای شماتیک این سیستم به صورت زیر می باشد.
جایی که سیستم اصلی به صورت زیر ساخته شده است.
همانطور که در بخش معرفی سیستم ها اشاره شد این سیستم در حالت معمول و با شرایط اولیه خاصی دارای رفتار آشوبناک به صورت زیر می باشد.
حال اکنون نشان می دهیم که روش خطی سازی ورودی – حالت، این رفتار سیستم غیر خطی را کنترل می کند و به عبارت دیگر عملکرد همواری را برای سیستم به دست می آورد.
نمای شماتیک سیستم کنترلی به صورت زیر می باشد.
…
قانون کنترل u و متغیر های جدید z و روابط جایگذاری قطب ها برای v مطابق آنچه که از روش تحلیلی به دست آمده اند در بخش سیمولینک وارد شده اند.
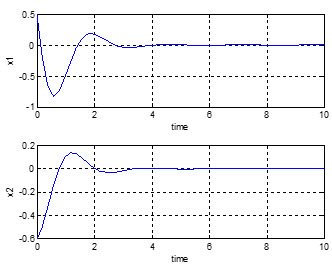
نتیجه زیر برای شرایط اولیه
و تنظیم پارامتر های کنترل به صورت
به دست آمده است.
نتیجه زیر برای همان پارامتر ها اما با شرایط اولیه به دست آمده است.
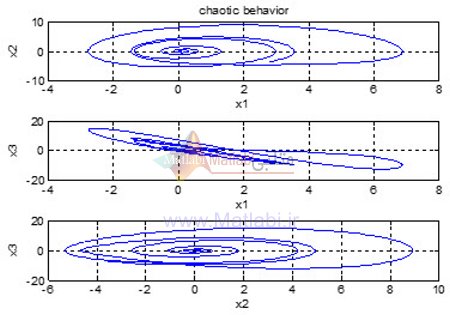
پرتره فازی حالت ها با این سیستم کنترلی به صورت زیر می باشد.
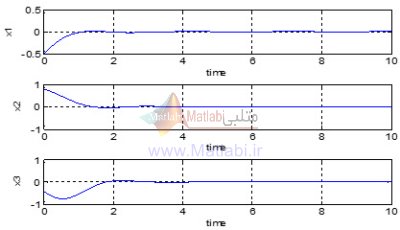
مشاهده می شود که رفتار آشوب حالت ها در این شرایط حذف شده است.
همچنین اگر رفتار حالت ها را با هم و در مقیاس زمانی نشان دهیم می بینیم که رفتار نوسانی نامنظم حالت ها به یک رفتار نرم و هموار تبدیل شده است.
این رفتار به صورت زیر می باشد.
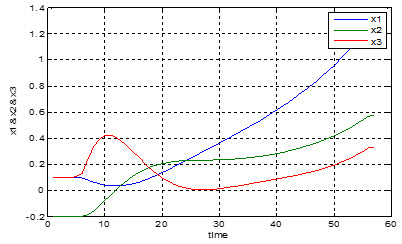
حال رفتار سیستم را در شرایط اولیه صفر و تحت اعمال ورودی پله بررسی می کنیم.
برای این منظور دو نمونه نتیجه شبیه سازی که نتیجه تنظیم متفاوتی از پارامتر های کنترل است را ارائه می کنیم.
لازم به ذکر است که مسئله ردیابی در این قسمت به این صورت است که حالت x1 باید ورودی پله را دنبال کند .
دو حالت دیگر باید به طور مجانبی پایدار شوند.
با تغییراتی که در پارامتر های کنترلی صورت گرفت نتیجه گرفتیم که بین خطای حالت دائم سیستم و میزان اورشوت باید مصالحه ای انجام دهیم.
متاسفانه مسئله ردیابی در این قسمت علی رقم تغییرات بسیار زیاد در پارامتر های کنترلی به نتیجه مطلوب نرسید.
در زیر دو نمونه از این نتایج دیده می شود.
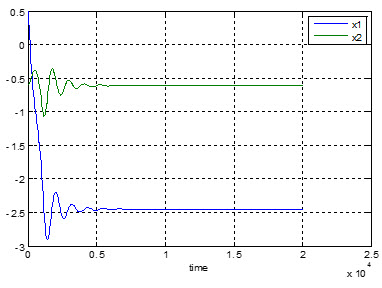
در این قسمت رفتار سیستم را تحت اعمال یک اغتشاش پله بررسی می کنیم.
برای این منظور یک ورودی پله را با ورودی کنترل سیستم غیر خطی در شرایطی که سیستم کنترلی نیز قرار داده شده است اعمال می کنیم.
نتیجه این اغتشاش ناپایداری سیستم کنترلی می باشد که شکل آن را در زیر مشاهده می کنید.
حال همین سیستم را در شرایطی که پارامتر های سیستم تغییر کنند بررسی می کنیم .
با تغییر پارامتر های سیستم به صورت c=-7 و b=-.4 و a=-2 نتیجه زیر از شبیه سازی به دست آمده است.
نتیجه ای که از شکل های بالا می گیریم این است که روش خطی سازی فیدبک یک روش کنترلی مقاوم نیست و نسبت به اغتشاش یا تغییر پارامتر ها مصون نیست.
سیستم (2)
در این قسمت فقط نتایج شبیه سازی را برای نشان دادن اعتبار این روش در مورد سیستم های مختلف نشان می دهیم.
سیستمی که در اینجا مورد استفاده قرار گرفته شده است به صورت زیر می باشد.
در این سیستم متغیر های جدید به صورت زیر می باشند.
قانون کنترل مناسب به صورت زیر خواهد بود.
در نتیجه معادلات حالت جدید برابر خواهد بود با:
نتیجه شبیه سازی این سیستم به صورت زیر می باشد.
1) بدون پیاده سازی سیستم کنترلی
2) با پیاده سازی سیستم کنترلی
روش خطی سازی ورودی – خروجی
سیستم (1)
سیستم اول که در روش ورودی – خروجی به کار گرفته شده است به صورت زیر می باشد.
با دو بار مشتق گیری از معادله خروجی رابطه بین ورودی و خروجی به صورت خطی و صریح یافت می شود.
این رابطه به صورت زیر می باشد:
در این صورت قانون کنترل به صورت زیر خواهد شد:
در نتیجه با انتخاب v به صورت
دینامیک خطای ردیابی سیستم به صورت زیر خواهد شد:
…
با روابط بالا نتیجه شبیه سازی برای این سیستم به صورت زیر خواهد بود:
خروجی تعریف شده برای این سیستم حالت x3 و هدف ما این است که این حالت، ورودی پله را به عنوان مسیر مطلوب ردیابی کند.
خروجی سیستم در حالتی که سیستم کنترلی روی سیستم اصلی اعمال نشده است به صورت زیر می باشد.
بعد از قرار دادن سیستم کنترلی در سیستم اصلی خروجی سیستم به صورت زیر می باشد.
شکل زیر پایداری دو حالت دیگر را همراه با ردیابی حالت سوم نشان می دهد.
شکل زیر اثر اغتشاش پله به ورودی کنترل را نشان می دهد که در آن باعث اختلال در عمل ردیابی سیستم کنترلی شده است.
نتیجه بالا این است که روش خطی سازی ورودی – خروجی نیز نسبت عدم قطعیت یا اغتشاش مقاوم نیست.
سیستم (2)
سیستم دوم مورد استفاده در این قسمت به صورت زیر می باشد.
با دو بار مشتق گیری از معادله خروجی رابطه بین ورودی و خروجی به صورت خطی و صریح یافت می شود.
این رابطه به صورت زیر می باشد.
در نتیجه قانون کنترل به صورت زیر خواهد بود.
در این صورت با انتخاب v به صورت
دینامیک خطای ردیابی سیستم به صورت زیر خواهد بود.
…
بنابراین مسئله ردیابی مسیر مطلوب، به تنظیم صحیح پارامتر های کنترل یعنی k1,k2 بستگی دارد.
طبق آنچه که در بالا به دست آمد نتیجه شبیه سازی برای این سیستم به صورت زیر می باشد.
در این سیستم هدف این است که خروجی سیستم که همان x1 است مسیر مطلوب سیستم که همان ورودی پله است را دنبال کند.
خروجی سیستم بدون اعمال سیستم کنترلی به صورت زیر می باشد.
…
بعد از قرار دادن سیستم کنترلی خروجی سیستم به صورت زیر درآمد که گویای ردیابی خوب این سیستم کنترلی است.
نتیجه گیری
روش خطی سازی فیدبک با تکنیک حذف اثر غیر خطی یک سیستم دینامیکی و استفاده از ابزار های کنترل خطی برای رسیدن به اهداف کنترلی یک روش طراحی کنترل کننده آسان و قابل فهم برای انواع زیادی از سیستم هاست.
در این گزارش سعی بر آن شد تا هر دو نوع روش خطی سازی فیدبک برای چهار نوع سیستم متفاوت اعمال شود تا نحوه عملکرد این روش روی سیستم به خوبی تحلیل شود.
سیستم اصلی مورد استفاده در این گزارش یک سیستم با رفتار نامنظم یا آشوبناک بود که با روش خطی سازی ورودی – حالت رفتار پایدار و همواری را برای سیستم به دست آوردیم.
آنچه که مشخص است این است که این روش قابلیت پایدارسازی داخلی یک سیستم و همچنین ردیابی یک مسیر مطلوب را به خوبی انجام می دهد.
اگر چه این روش محدودیت هایی دارد که در بخش های مختلف گزارش به آن اشاره شد.
از آن جمله اینکه قانون کنترل به دست آمده به طور معمول دارای نقاط تکین می باشد و از طرفی در بعضی موارد خیلی بزرگ می باشد.
از طرفی این روش به شدت به مدل سیستم وابسته است و در برابر عدم قطعیت و اغتشاش مصون نیست و این مسئله در مورد سیستم های مختلف گزارش بررسی شد.
کلید واژه : کنترل غیرخطی, خطی سازی فیدبک , تطبیقی, پروژه متلب, پروژه matlab , شبیه سازی با متلب
Adaptive feedback linearization control
شبیه سازی
Parametric convergence and control of chaotic system using adaptive feedback linearization
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.



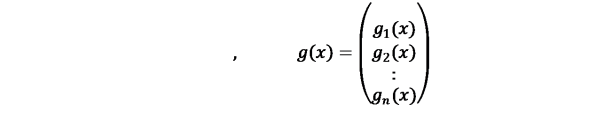







دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.