توضیحات
Non-Adaptive Sliding Mode Controllers in Terms of Inertial Quasi-Velocities
ترجمه فارسی مقاله: کنترلرهای مود لغزشی تطبیق ناپذیر بر حسب شبه سرعتهای ساکن
فقط بخشی از توضیحات اینجا آمده است. جهت دریافت شبیه سازی به همراه گزارش کامل باید این محصول خریداری شود.
1-معرفی
مساله ی کنترل مسیر زمانی ایجاد میشود که نیاز باشد یک بازوی مکانیکی (manipulator)، یک مسیر را دنبال کند.
در متون رباتیک برای رسیدن به این هدف دو رویکرد استفاده میشود:
محاسبه کننده گشتاور (کنترل معکوس مکانیکی) و کنترل مود لغزان (Sciavicco & Siciliano (1996); Slotine & Li (1991)). سیستم تحت کنترلر معکوس دینامیکی، خطی است و نسبت به ورودی های جدید جدا میشود.
در متون رباتیک روش مود لغزان که توسط Slotine & Li (1987; 1991) تشریح شده است، معمول است.
این روش، با روش قبل متفاوت است؛
چرا که حتی اگر معادلات بازوی مکانیکی دقیقا نیز معلوم باشد، معادلات حرکت آن، خطی نمی شود.
استراتژی های کنترل مود لغزان در صفحه زانوی بازوی مکانیکی استفاده می شود و بعلاوه در فضای عملیاتی آن هم کاربرد دارد (Sciavicco & Siciliano (1996); Slotine & Li (1987; 1991)).
از دیدگاه عملی برای مسیریابی (tracking) مکان عملگر نهایی (end effector)، برای بازوی مکانیکی راحت تر از تنطیم مکان زانو است؛ چرا که عمل مستقیما انجام می شود.
مساله ی کنترل حرکت در صفحه ی بازوی مکانیکی در مرجع مورد بررسی قرار گرفته است Kelly & Moreno (2005); Moreno & Kelly (2003); Moreno et al. (2003); Moreno-Valenzuela & Kelly (2006).
بعضی مواقع مدل اصطکاک نیز در نظر گرفته شده است؛ برای مثال: Moreno et al. (2003); Moreno-Valenzuela & Kelly (2006). یکی از کابردهای شناخته شده ی رویکرد مودهای لغزان این است که به شخص اجازه می دهد که یک شکل را کنترل کند Mochiyama et al. (1999).
به منظور طراحی نسخه های مختلف قانون لیاپانوف برای تنظیم بازوی مکانیکی ربات توسط Santibanez & Kelly (1997); Spong (1992) بر حسب IQV نیز در مرجع Herman (2009b). معرفی شده است.
تعریف کلاسیک منجر به بدست آمدن معادلات دیفرنسیل غیر خطی مرتبه 2 میشود.
این معادلات شامل بردارهای تعمیم یافته ی مکان و سرعت که بیانگر صفحه زانوی بازوی مکانیکی است می باشد. با این وجود، برای اهداف کنترلی، کار با معادلات مرتبه اول حرکت با ماتریس قطری نسبت به معادلات مرتبه 2، راحت تر است.
لحاظ کردن دینامیک های مکانیکی سیستم با استفاده از شبه سرعت ها و هندسه تفاضلی (diffrential geometry) امکان پذیر است (Kwatny & Blankenship (2000)).
معادلات مرتبه اول بدست آمده بصورت صورت poincares معادلات لاگرانژ است.
یکی از راه های مفید که منجر به ماتریس قطری یا ماتریس اینرسی واحد می شود، توسط آنچه IQV نامیده میشود، معرفی میشود.
چندین روش وجود دارد که چنین امری را ممکن میکند (برای مثال Hurtado (2004); Jain & Rodriguez (1995); Junkins & Schaub (1997); Loduha & Ravani (1995); Sovinsky et al. (2005)).
روشی که در Hurtado (2004) معرفی شده است با روش تجربی chelosky همراه است (Sovinsky et al. (2005)). در روشی که توسط Jain & Rodriguez (1995) تشریح شده است، شبه سرعت های نرمالایز شده (NQV) معرفی شده اند.
روش بعدی، روش Junkins & Schaub (1997)است که مبتنی بر محاسبه ی مقادیر ویژه و بردارهای ویژه ماتریس اینرسی است.
Loduha & Ravani (1995) مولفه های تعمیم یافته ی سرعت (QVC) را پیشنهاد میکند که به معادلات اصلاح شده ی kane مربوط است (برای مثال Kane & Levinson (1983)). سرانجام مولفه های نرمالایز شده ی تعمیم یافته ی سرعت (NQVC) در مرجع Herman (2005b; 2006) لحاظ شده است.
NGVC یک شکل مفید از GVC است.
ایده ی کلیدی مقاله، بررسی کنترلرهای مود لغزان سازگارناپذیر با آن شده بر حسب Inertial Quasi-Velocities (IQV)است.
IQV به این معنی است که شبه سرعت ها شامل پارامترهای حرکت شناسی و دینامیک برای بازوی مکانیکی صلب است.
بعلاوه شامل ابعاد هندسی نیز می باشند. برخلاف آنکه چندین IQV وجود دارد، فقط برخی از آنها اینجا بررسی شده اند. GVC در Loduha & Ravani (1995)تشریح شده، NQV در Jain & Rodriguez (1995)داده شده و NGVC در Herman (2005b; 2006)داده شده است.
این به این دلیل است که این نوع IQV به خوبی ایده ی کنترل مودهای لغزان را با استفاده از NQV مورد اشاره قرار می دهد.
همچنین نشان داده شده است که اگر سیستم تحت قانون کنترلی پیشنهادی لحاظ شود، چه مزیت هایی قابل مشاهده خواهد بود.
یکی از مزیت ها در نتیجه این واقعیت است که IQV در انرژی جنبشی تجزیه شده و منجر به تجزیه ی ماتریس های اینرسی بازوی مکانیکی میشود.
در نتیجه، با لحاظ شدن اینرسی، کوپلینگ دینامیکی میتواند تعیین شود. بعلاوه، برخی معایب رویکرد کنترل IQV نشان داده شده است.
هدف سوم نشان دادن این است که کنترلرهای مود لغزان در صفحه زانوی بازوی مکانیکی، محقق شده است.
علاوه بر این، میتوان اغتشاشات(که اینجا توسط تابع میرایی viscous نشان داده شده است) را نیز لحاظ کرد که به فرد اجازه میدهد تا نتایج را برای مدلهای مختلف اصطکاک توسعه دهد.
مقاله به این صورت سازمان دهی شده است. بخش 2، معادلات قطری حرکت بر حسب IQV را بدست میدهد.
در بخش 3، کنترلرهای لغزان در صفحه زانو برای یک بازوی مکانیکی و همچنین صفحه عملکرد آن معرفی میشود.
نتایج شبیه سازی با مقایسه عملکرد میان طرح های جدید کنترل و کنترلرهای کلاسیک برای 2 مدل سری بازوی مکانیکی به نام های ربات 3 N.O.F فضایی DD Am و ربات Yasukawa در بخش 4 آمده است.
بخش آخر شامل نتیجه گیری و پیشنهاداها برای تحقیقات آینده است.
2-دینامیک ها بر حسب شبه سرعت های ساکن
2-1-علامت گذاری
بردارهای مکان، سرعت و شتاب تعمیم یافته
تعداد درجه های آزادی
ماتریس اینرسی سیستم
بردار corolis و نیروی گریز از مرکز در معادلات حرکت کلاسیک
بردار نیروی گرانشی در معادلات حرکت کلاسیک
بردار نیروهای ناشی از اصطکاک (میرایی ویسکوز) که وابسته به بردار سرعت زانو
است که F یک ماتریس قطری معین مثبت
شامل ضرایب میرایی برای همه زانو ها است.
بردار نیروهای تعمیم یافته
ماتریس قطری اینرسی سیستم بر حسب GVC
مولفه های بردار سرعت تعمیم یافته و مشتق زمانی آن
ماتریس تبدیل بالا مثلثی میان بردار سرعت
و مولفه های بردار سرعت تعمیم یافته Loduha & Ravani (1995)
مشتق زمانی ماتریس Y(θ)
بردار coliolis و نیروهای گریز از مرکز بر حسب GVC
بردار نیروهای گرانشی بر حسب GVC
بردار نیروی اصطکاک بر حسب GVC
بردار شبه نیرو بر حسب GVC
به ترتیب بردار شبه سرعت NGVC و مشتق زمانی آن
ماتریس تبدیل بالا مثلثی سرعت بر حسب NGVC
مشتق زمانی ماتریس
بردار coriolis و نیروهای گریز از مرکز بر حسب NGVC
بردار نیروهای گرانشی بر حسب NGVC
بردار اصطکاک بر حسب NGVC
بردار نرمالایز شده شبه نیرو
بردار نرمالایز شده شبه سرعت
بردار coriolis و نیروهای گریز از مرکز در NQV
بردار نیروی گرانشی در NQV
عملگر فضایی ریشه دوم ماتریس اینرسی
مشتق زمانی ماتریس M(θ)
- بردار نرمالایز شده شبه نیرو بر حسب NQV
اینرسی تقسیم شده اطراف ماتریس محورهای زانو matrix Jain & Rodriguez (1995)
عملگر ترانهاده
بخشی از ترجمه در اینجا آورده نشده و با خریداری شبیه سازی مقاله بدست شما خواهد رسید.
3-2-روش های تجزیه ی دیگر
مساله ی حضور در خصوص تبدیل معادلات حرکت روشی است که برای تجزیه ی ماتریس اینرسی بکار می رود. روش های شناخته شده ی زیادی برای تجزیه ی ماتریس اینرسی برای بدست آوردن ماتریس قطری یا ماتریس واحد وجود دارد.
به این منظور از طریق فاکتورگیری Colesky (Hurtado (2004); Matlab (1996); Sovinsky et al. (2005)) یا تجزیه به مقادیر ویژه که در مرجع Junkins & Schaub (1997); Matlab (1996) لحاظ شده است، اشاره کرد.
به علاوه با استفاده از برای مثال تجزیه ی schur و روش تجزیه ی مقادیر ویژه Matlab (1996) میتوان ماتریس اینرسی را تجزیه کرد. روش تجزیه ی مبتنی بر مقادیر ویژه و بردارهای ویژه، روش تجزیه ی schur و روش مقادیر ویزه برای یک ماتریس معین مثبت M منجر به بدست آمدن یک ماتریس تبدیل می شود که بطور کلی همه عناصر آن غیر صفراند.
این حقیقت طراحی کنترلر را پیچیده می کند؛ چرا که تعداد عملگر ها و متغیرهای عددی لازم افزایش می یابد. با این وجود، گاهی اوقات استفاده از روش متناسب (که زیاد وقت گیر نباشد) ممکن است تصمیم به استفاده از روش کنترل مود لغزان سازگار ناپذیر بگیرد.
4-2-برخی ویژگی های مفید IQV
برخی مزیت های بدست آمده از تعریف حرکت بر حسب IQV در خصوص دیدگاه آن به دینامیکهای بازوی مکانیکی می باشد. انرژی جنبشی بازوی مکانیکی بر اساس مقایسه مراجع Herman (2005a), Jain & Rodriguez (1995), and Herman (2005b) به دست آمده است.
گزارش شبیه سازی با متلب :
شبیه سازی ربات دو درجه آزادی با کنترلر های PID و مد لغزشی
(مدل سازی با در نظر گرفتن شبه سرعت های ایستا)
سیستم ربات بازو دارای ساختاری مبتنی بر دینامیک ربات می باشد .
معادلات دینامیکی سیستم در محیط سیمولینک حاوی دو ترم موقعیت و سرعت می باشد.
با توجه به ترم های غیر خطی موجود در دینامیک سیستم اولین گام جهت دستیابی به ساختار کنترلی مطلوب ، استفاده از روش های خطی سازی است.
در این پروژه ابتدا به روش فیدبک خطی ساز دینامیک های غیرخطی سیستم حذف شده و سیستم دینامیکی شبه خطی خواهد داشت.
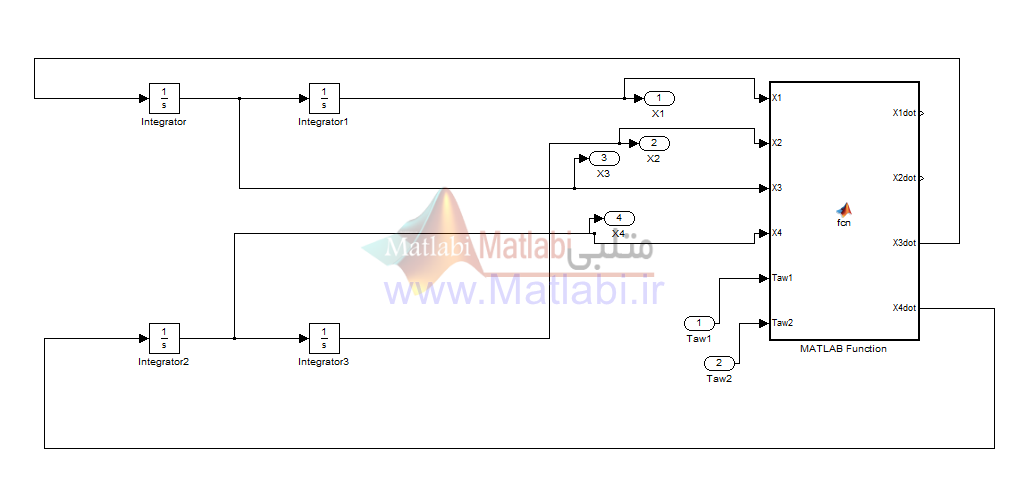
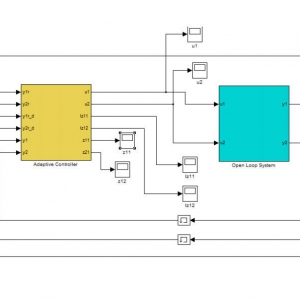
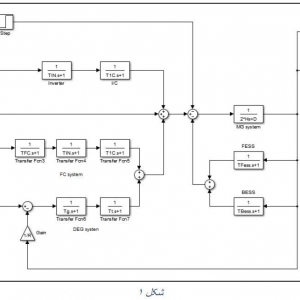
شکل 1 – دینامیک غیرخطی ربات
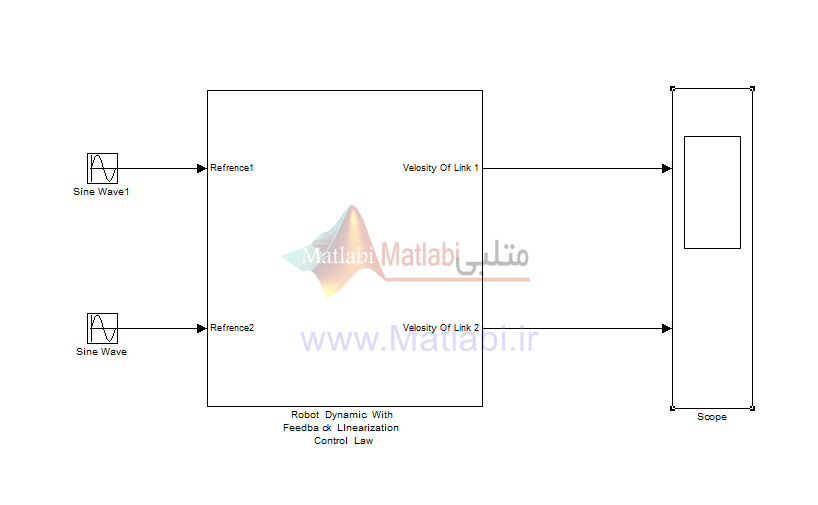
شکل 2 – ساختار حلقه بسته پلانت
همانطور که در ساختار شبه خطی بالا مشخص است رفتار سیستم مشابه رفتار سیستم های خطی می باشد.
علت سرزدن این رفتار از دینامیک غیر خطی طراحی سیگنال کنترلی به فرم زیر جهت خطی سازی المان های غیرخطی می باشد:
…
شکل 3 – فیدبک خطی ساز
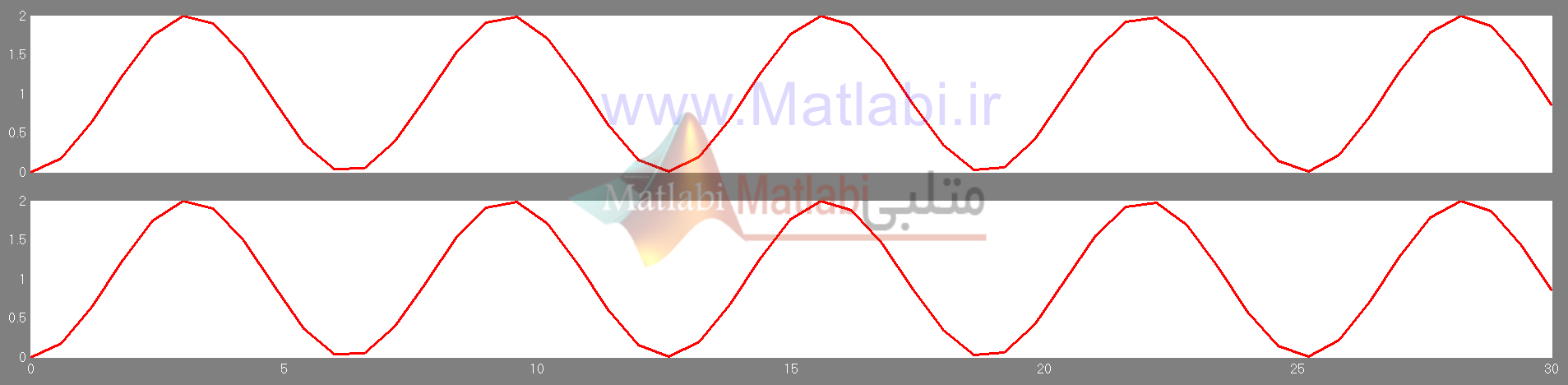
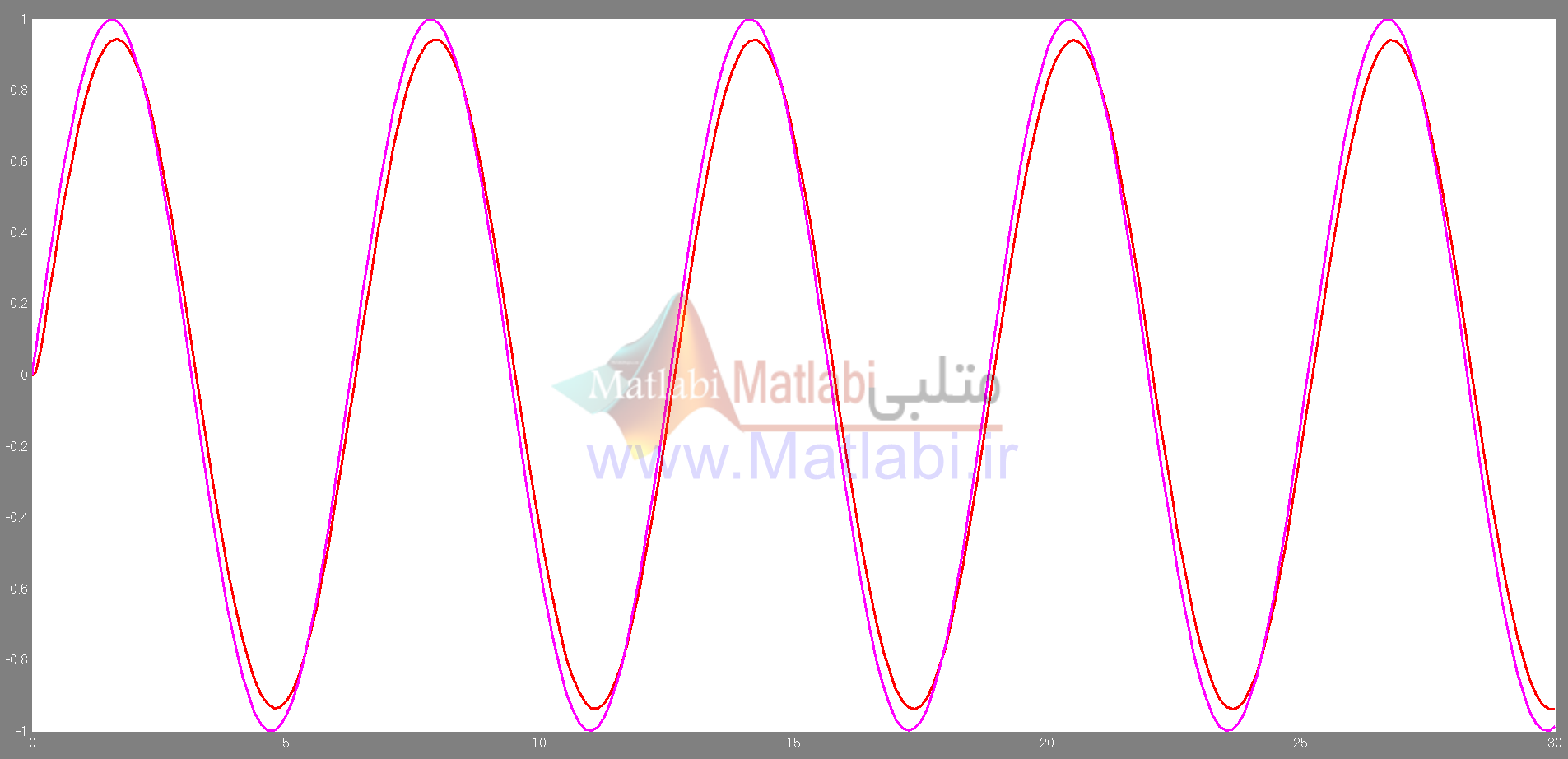
شکل4 – پاسخ سیستم خطی سازی شده
کنترلر PID :
این کنترلر یکی از معمول ترین و کاربردی ترین کنترل کننده های موجود در صنایع است که علی رغم سادگی قابلیت های کنترلی مناسبی به همراه مقاومت نسبتا مطلوبی می باشد.
با این وجود طراحی کنترلر PID در حضور وجود دینامیک های غیر خطی در ساختار پلنت مشکلی اساسی جهت دستیابی به عملکرد مطلوب می باشد.
…
شکل 5 – طراحی کنترلر PID

شکل 6– پاسخ سیستم در حضور کنترلر PID
کنترلر مد لغزشی :
به دنبال ایده طراحی کنترلر و ایجاد مفهوم حساسیت کنترل مد لغزشی با در نظر گیری کرانی بر روی عدم قطعیت ها و اغتشاش سیستم سیگنال کنترلی را ایجاد خواهد نمود که نسبت به موارد یاد شده دارای مقاومت بالایی می باشد.
یکی ازمهمترین دلایل استفاده از کنترل مد لغزشی افزایش مقاومت سیستم در برابر عدم قطعیت ها می باشد.
به طور خلاصه طراحی کنترلر مد لغزشی شامل دو فاز می باشد.
- فاز ریچینگ
- فاز رباستنس (ماندن روی سطح لغزش)
در این روش ابتدا با تعریف سطح لغزش مورد نظر به فرم استاندارد سیگنال کنترلی را به نحوی طراحی می کنند تا سیستم ضمن رسیدن به سطح لغزش مورد نظر علی رغم وجود عدم قطعیت و اغتشاش بر روی آن بماند.
این کنترلر در حقیقت متشکل از ساختار فیدبک حالت (فاز ریچینگ) و یک سیگنال سوئیچینگ (فاز مقاومت) می باشد.
شکل 7 – طراحی کنترلر مد لغزشی
شکل 8– پاسخ سیستم در حضور کنترلر Sliding Mode
استفاده از سیگنال سوئیچینگ باعث افزایش حاشیه پایداری سیستم خواهد شد اما وجود منطق سوئیچ زنی منجر به ناپیوستگی سیگنال کنترلی و در نتیجه آسیب رسیدن به عملکرد های مکانیکی و تحریک دینامیکهای مدل نشده فرکانس بالا می شود.
که به این پدیده اصطلاحا وزووز کردن یا چترینگ می گویند. ایده طراحی کنترلر مد لغزشی مرتبه بالا به منظور کاهش پدیده مذکور می باشد.
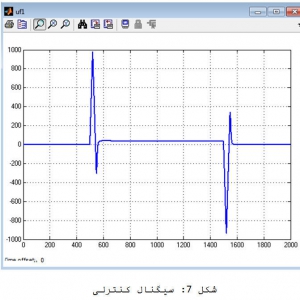
شکل 9 – سیگنال ورودی کنترلر مد لغزشی ( پدیده چترینگ)
همانطور که در شکل فوق مشخص است وجود سیگنال کنترلی مد لغزشی در متغیر کنترلی دوم (سرعت لینک دوم) باعث پدیده چترینگ بالا و ایجاد آسیب های بعدی به فرایند کنترل خواهد شد.
جهت کاهش اثر مشکل ایجاد شده از طراحی کنترلر مد لغزشی مرتبه بالا استفاده شده است که نتایج حاوی بهبود کیفیت سیگنال کنترلی متغیر سرعت لینک دوم می باشد.
…
شکل 10 – طراحی کنترلر مد لغزشی مرتبه بالا
شکل 11 – طراحی کنترلر مد لغزشی مرتبه بالا
شکل 12 – سیگنال کنترلر مد لغزشی مرتبه بالا
شبیه سازی مقاله Non-Adaptive Sliding Mode Controllers in Terms of Inertial Quasi-Velocities
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.









دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.