توضیحات
MOGSA, A Gravity Inspired Multi-Objective Meta-heuristic
یک روش فرا ابتکاری مبتنی بر گرانش برای مسایل چند هدفه متوالی بردار پشتیبان
مقدمه:
در مسایل عملی، مسایل بهینه سازی به صورت یافتن یک جواب که یک تابع هدف را مینیمم (یا ماکزیمم) میکند نیسّتند و معمولا میخواهیم تعدادی تابع هدف را مینیمم سازی نماییم. در این موارد یک نقطه بهینه سراسری وجود ندارد و با یک دسته از جوابهای نامغلوب مواجهیم.
بنابراین اگر الگوریتم بهینه سازی به درستی تنظیم نشده باشد جوابها به شدت مورد تاثیر قرار میگیرند.
الگوریتم جستجوی گرانشی (GSA) که در سال 2009 توسط راشدی و همکاران ارائه شد، یکی از قوانین مهم طبیعت یعنی گرانش را تقلید میکند.
نیرویی که بین دو جرم وجود دارد عبارت است از:
که در آن F اندازه نیروی گرانش و M1 و M2 جرم جسمهای اول و دوم میباشد. در رابطه بالا G ثابت گرانش است که معمولا آنرا به صورت متغیر با زمان زیر در نظر میگیریم:
با توجه به رابطه بالا، شتابی که بر اثر نیروی گرانش ایجاد میشود عبارت است از:
زمانی که چند جرم بر یکدیگر نیرو وارد میکنند، برآیند نیروهای وارد بر هریک محاسبه میگردد (شکل زیر).
در شکل بالا نیروی وارد بر جرم i از طرف جرم j است. بر اساس این توضیحات، الگوریتم جستجوی گرانشی معرفی میگردد.
الگوریتم جستجوی گرانشی
در این بخش الگوریتم بهینه سازی با الهام از نیروی گرانش معرفی میگردد.
در این الگوریتم جوابها به صورت اشیائی در نظر گرفته میشوند که عملکردشان بر اساس جرم آنها تعیین میگردد. تمام این جوابها بر اساس نیروی گرانش یکدیگر را جذب میکنند.
سیستمی با N عامل (جواب) را در نظر بگیرید. موقعیت عامل i اُم به صورت زیر تعریف میشود:
که در آن موقعیت i اُمین عامل در d اُمین بعد را نشان میدهد. در زمان t نیروی بین جرم i و جرم j به صورت زیر نشان داده میشود:
که در آن . برای ایجاد یک مشخصه تصادفی در الگوریتم فرض میکنیم که برآیند نیروهایی که به عامل i وارد میشود مجموع کل نیروها با وزنهای تصادفی در بازه [0 1] است:
که در آن یک عدد تصادفی در بازه [0 1] است.
بر اساس قانون حرکت، شتاب جسم i در بعد d برابر است با:…
با استفاده از شتاب، سرعت جسم به صورت زیر به روزرسانی میشود:…
سپس با استفاده از سرعت، موقعیت به صورت زیر به روز رسانی میشود:…
فرض میکنیم جرمهای اکتیو و پسیو برای جرمهای مختلف یکسان باشد:…
در این حالت جرم هر ذره به صورت زیر محاسبه میشود:…
در رابطه بالا برای مسایل مینیمم سازی:…
الگوریتم توضیح داده شده در بالا در فلوچارت زیر نمایش داده میشود:
بهینه سازی چند هدفه
در بهینه سازی چند هدفه بر خلاف بهینه سازی تک هدفه به جای یک جواب بهینه، با مجموعهای از جوابها مواجه هستیم. این جوابها نامغلوب[1] هستند. جواب نامغلوب به این معنی است که مقدار حداقل یک تابع هدف برای این جواب در بین تمام جوابها مینیمم است.
روش معمول در روشهایی مانند PSO این است که در هر تکرار یک جواب را به عنوان جواب پیشرو در نظر میگیریم و باقی جوابها را به سمت این جواب حرکت میدهیم.
بنابراین تفاوت این جوابها در نحوه انتخاب کردن جواب پیشرو است.
مثلا روشها انتخاب تصادفی و یا با استفاده از عملگر جهش تا به حال پیشنهاد شده است.
اما انتخاب تنها یک جواب از بین تمامی جوابها به عنوان جواب پیشرو به معنی این است که باقی جوابها را نادیده گرفته ایم. در این حالات الگوریتم به سمت یک بهینه محلی همگرا میگردد و در آن گرفتار میشود.
در روش ارائه شده به جای در نظر گرفتن تنها یک جواب پیشرو، از اطلاعات تمام جوابها بر حسب مقدار گرانش آن استفاده میکنیم.
برای توضیح الگوریتم ابتدا باید مفهوم غلبه را در فضای جوابها توضیح دهیم.
میگوییم که جواب 1 بر جواب 2 غلبه دارد اگر مقدار بردار تابع هدف اولی در هیچ یک از ابعاد از دومی بیشتر نباشد.
بر اساس این تعریف، دستهای از جوابها را که حداقل در یک بعد از بردار تابع هدف، کمترین مقدار را در بین تمامی جوابها دارند، جوابهای نامغلوب مینامند.
جوابهای نامغلوب صف اول نیز نامیده میشوند.
اگر جوابهای نامغلوب را کنار بگذاریم، جوابهای غالب در بین جوابهای باقی مانده، جوابهای صف دوم نامیده میشوند. به همین ترتیب صف سوم و … را داریم.
برای داشتن یک معیار از یک جواب از مفهوم غلبه استفاده میکنیم.
به این ترتیب که ابتدا جوابها را به صورت نامغلوب بودن مرتب میکنیم و به هر کدام بر اساس صفی که در آن قرار میگیرند یک رتبه اختصاص میدهیم. مثلا به جوابهای صف اول 1، صف دوم عدد 2 و … را اختصاص میدهیم.
سپس با استفاده از این رتبهها مقدار جرم را برای هر جواب محاسبه میکنیم.
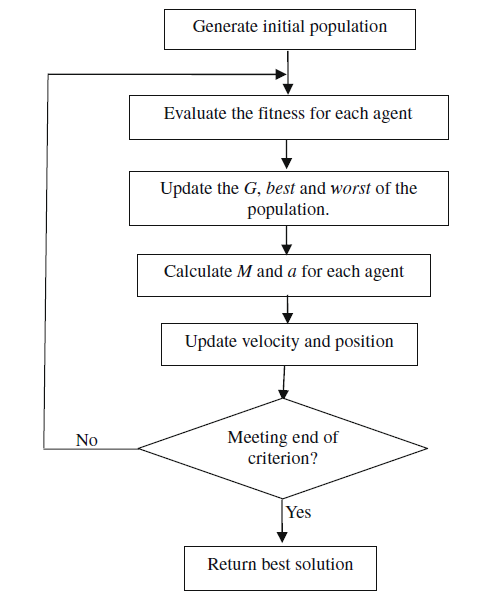
سپس نیروهای وارد بر هر جواب را توسط مقدار جرمها تعیین میکنیم وبا نیروها شتاب، سرعت و در نهایت موقعیت ذره به روز میشود. شکل زیر الگوریتم معرفی شده را نشان میدهد:
در الگوریتم بالا ابتدا جمعیت اولیه به صورت تصادفی در بازه مجاز تولید میشوند.
سپس مقدار سرعت اولیه صفر در نظر گرفته میشود. سپس جمعیت بر حسب غالب بودن مرتب میشوند و به هرکدام یک رتبه اختصاص داده میشود.
در مرحله بعد وارد یک حلقه تکرار میشویم و در هر تکرار مقادیر جرم و نیرو و سرعت و موقعیت به روز میشوند.
برای اطمینان از مجاز بودن جوابهای به روز شده، در این مرحله جوابها با کرانهای مجاز بالا و پایین مقایسه میشوند.
سپس جوابها بر اساس غلبه مرتب سازی میشوند و به همین ترتیب تکرارها ادامه پیدا میکنند.
توابع تست
در این پروژه از سه تابع چند هدف برای تست الگوریتم استفاده میکنیم.
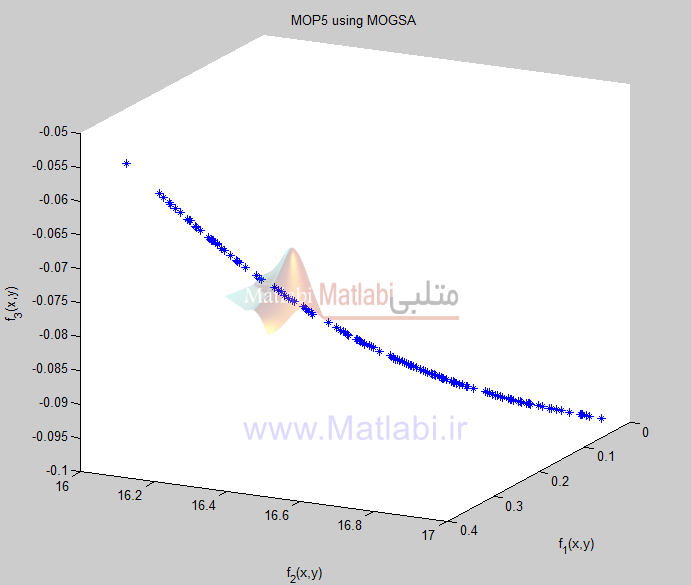
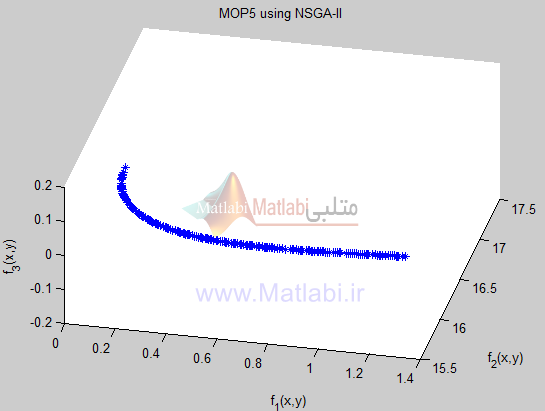
اولین تابع که MOP5 نامیده میشود به صورت زیر است:…
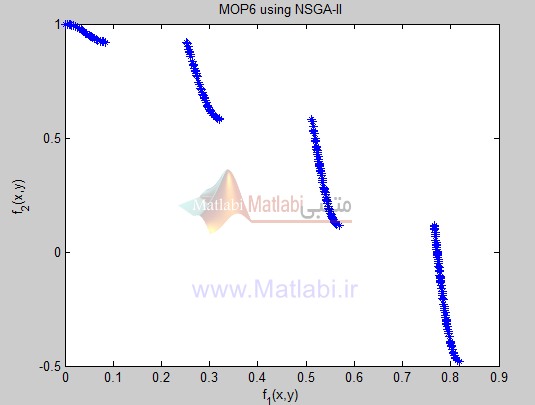
تابع بعدی که MOP6 نامیده میشود به صورت زیر است:…
تابع بعدی که MOP1 نامیده میشود به صورت زیر است:…
در پیاده سازی الگوریتم پارامترهای زیر را استفاده میکنیم:…
پیاده سازی در Matlab
برنامههای نوشته شده برای هر سه دست تابع هزینه یکسان است و فقط در تابع evaluate_objective که تابع هدف را پیاده سازی میکنند متفاوت هستند. پس به توضیح یکی از آنها اکتفا میکنیم. فایل main.m برنامه اصلی و اجرایی ما است. در ابتدای برنامه پارامترهای الگوریتم تنظیم میشود:
pop = 200;
max_it = 500;
up=5;
low=0;
M=2;
dim=2;
سپس جمعیت جوابها توسط تابع initialize_variables مقداردهی اولیه میشوند. در این تابع یک حلقه تکرار for برای تک تک جوابهای مورد نیاز داریم:
…
سپس در یک حلقه for دیگر تمام ابعاد ذره i اُم را با توجه به کرانهای بالا و پایین مجاز تعریف شده (up و low) تعیین میکنیم.
…
در نهایت مقدار بردار تابع هدف در جواب تولید شده محاسبه شده و در کنار آن جواب قرار داده میشود:
…
حلقه مربوط به شمارشگر i بسته میشود:
…
همانطور که دیده میشود برای محاسبه مقدار تابع هدف از برنامه evaluate_objective استفاده کردهایم. در این تابع مقدار تابع هدف از روی بردار ورودی X بر اساس روابط تعریف شده در مقاله در تک تک توابع هدف یک مساله تعیین میشود. مثلا برای تابع MOP1 داریم:
…
در ادامه برنامه اصلی main.m بردار سرعت هر جواب به صورت بردار صفر مقدار دهی اولیه میگردد:
V=zeros(pop,dim);
سپس وارد یک حلقه for با متغیر شمارشی iteration میشویم. این حلقه مربوط به تکرارهای الگوریتم GSA است:
for iteration = 1 : max_it
در هر تکرار عملیات زیر به صورت متوالی انجام میگیرد:
1-مقدار جوابها در تکرار قبل در متغیر old_X ذخیره میشوند:
old_X=X;
سپس جوابها بر اساس نامغلوب بودن مرتب میشوند و به انتهای هر جواب و در کنار بردار هدفی که قبلا قرار دادیم، دو عدد دیگر اضافه میشود. یکی رتبهای است که به آن جواب بر اساس شماره صفش داده میشود و دیگری فاصله از جمعیت است که بر اساس فاصله ای است که هر جواب از جوابهای هم صفش دارد و طبق رابطه زیر محاسبه میشود:
که در این رابطه داریم:
در واقع این عدد معیاری از پراکندگی دادهها در هر صف میباشد. دستور این عملیات به صورت زیر است:
X = non_domination_sort_mod(X,dim);
تابع non_domination_sort_mod.m که در خط بالا استفاده شده، با دریافت ماتریس جوابهای X و بُعد فضای جوابها (dim)، آنها را بر اساس رتبه صفشان مرتب کرده و مقدار رتبه و فاصله از جمعیت را در انتهای آنها قرر میدهد. یعنی هر سر از ماتریس X به صورت زیر در میآید:
| مقدار فاصله از جمعیت | مقدار رتبه (شماره صف) | بردار تابع هدف | بردار جواب (dim تایی) |
با توجه به این که ترتیب جوابها در خط بالا توسط تابع non_domination_sort_mod.m تغییر میکند و لازم است که ترتیب سرعتها (V) نیز بر همین اساس تغییر کند، با استفاده از برنامه ind_sort.m ترتیب اندیسهای جدید را از روی ماتریسهای old_X و X تعیین کرده و ماتریس V را بر اساس این اندیسها مرتب میکنیم:
…
در تابع ind_sort ابتدا یک بردار خالی بر اساس تعداد جوابها ایجاد میشود تا بعدا توسط اندیس های جابجا شده پر شود:
[N M]=size(V);
ind=zeros(1,N);
سپس در دو حلقه for جوابهای موجود در old_X و X یکی یکی با هم مقیسه میشوند و هر جا دو جواب از آندو دقیقا با هم برابر بود این نشان دهنده اندیس جدید آن جواب است و این اندیس ذخیره میگردد:
for i=1:N
for j=1:N
if all(V(j,:)==X(i,:))
ind(i)=j;
end
end
end
ادامه برنامه main.m:
در ادامه عملیات حرکت دادن جوابها بر اساس الگوریتم گرانش بر روی جوابها اعمال میشود:
[X,V] = gsa_operator(X,V,iteration,max_it,dim);
برنامه gsa_operator با دریافت ماتریس جوابها، ماتریس سرعتهای متناظر، شماره تکرار، تعداد کل تکرارها و بُد فضای جوابها، جوابهای جدیدی بر اساس الگوریتم GSA تولید میکند. در برنامه gsa_operator ابتدا مقدار رتبه جوابها که در ستون یکی قبل از آخر از ماتریس X ذخیره شده را در متغیر fitness میریزیم:
…
سپس مقدار جرم هر جواب بر اساس مقدار رتبه آن توسط تابع masscalculation (که بعدا توضیح داده میشود) محاسبه میشود و در متغیر M ذخیره میگردد:
…
سپس مقدار ثابت گرانش که تابعی از شماره تکرارهاست توسط رابطة معرفی شده محاسبه میشود:
alfa=-1;G0=1.5;beta=7;
G=G0*(-alfa*iteration/max_it)^beta; %eq. 28.
در ادامه از تابع Gfield.m ( که بعدا توضیح داده میشود) استفاده کرده و مقدار بردار نیروی وارد بر هر ذره و در نتیجه شتاب آنرا محاسبه میکنیم:
…
با داشتن بردار شتاب، بردار سرعت به راحتی به روز میشود:
…
در نهایت با استفاده از سرعت ذره، موقعیت آن به روز میگردد:
…
برنامه masscalculation: این برنامه در ابتدا مقدار کمترین و بیشترین رتبه را که معادل با بهترین و بدترین جوابها هستند پیدا میکند:
…
اگر تمام رتبه ها برابر بودند تابع مقدار 1 را برای تمام اجرام در نظر میگیرد:
if Fmax==Fmin
M=ones(N,1);
در غیر اینصورت مقدار جرمها با استفاده از رابطه داده شده محاسبه میگردد:
else
best=Fmin;worst=Fmax; %eq.17-18.
M=(fit-worst)./(best-worst); %eq.15,
end
سپس یک نرمالسازی روی جرمها انجام میشود تا مقدار مجموع آنها برابر 1 گردد:
…
در برنامه Gfield ابتدا جرمها به صورت نزولی مرتب میشوند:
…
سپس برای هر ذره نیروهایی که از طرف دیگر ذرات وارد میشود محاسبه میشوند و سپس با یک وزن تصادفی با هم جمع می گردند:
…
سپس با استفاده از نیروی محاسبه شده، مقدار شتاب بدست میآید:
…
ادامه برنامه main.m: از آنجایی که ممکن است جوابهایی که در تکرار جدید تولید شدهاند خارج از رنج مجاز مساله باشند، با استفاده از تابع space_bound این جوابها را در رنج قرار میدهیم:
X(:,1:dim)=space_bound(X(:,1:dim),up,low);
تابع space_bound هر بعد از جواب را با ابعاد مجاز مقایسه میکند و در صورت خارج از رنج بودن آن، مقدار آن را در حد بالایی یا پایینی رنج قرار میدهد:
function X=space_bound(X,up,low)
[N,dim]=size(X);
for i=1:N
X(i,X(i,:)>up)=up;
X(i,X(i,:)<low)=low;
end
در اینجا حلقه تکرارهای الگوریتم تمام میشود و جوابهای موجود در صف اول نمایش داده میشوند:
X=X(X(:,end-1)==1,:);
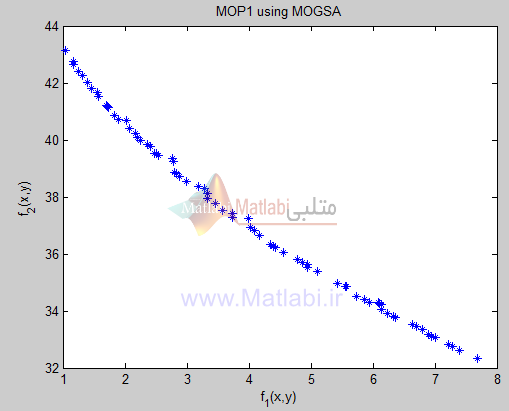
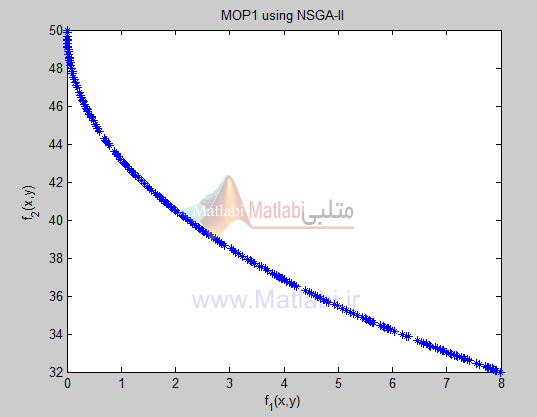
plot(X(:,dim + 1),X(:,dim + 2),’*’);
title(‘MOP1 using MOGSA’);
xlabel(‘f_1(x,y)’);
ylabel(‘f_2(x,y)’);
نتایج شبیه سازی با متلب
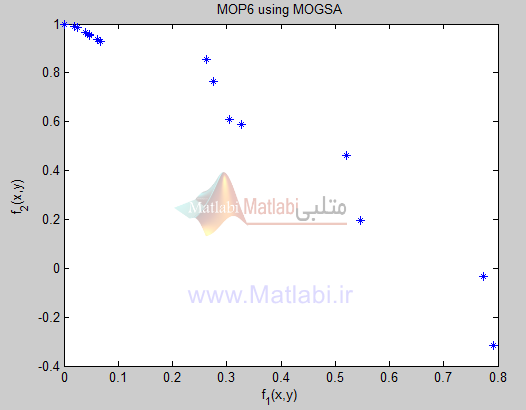
شکلهای زیر نتایج اجرای الگوریتم را بر روی توابع تست معرفی شده نشان میدهد. همچنین مقدار فاصله از جمعیت نیز برای ارائه یک معیار کمی محاسبه و نمایش داده شده است:
برنامه مربوط به اجرای الگوریتم فایل nsga_2.m است که در آن با تنظیم پارامتر pro بر روی 1،2 یا 3 میتوان مسایل MOP5،MOP6 و یا MOP1 را حل نمود:
pop = 200;
gen = 50;
pro = 2;
- Non-dominated ↑
کلید واژه : بهینه سازی,پروژه متلب,شبیه سازی با متلب,matlab project,پروژه های matlab,
Multi-objective Particle Swarm Optimization (MOPSO), Multi-objective Gravitational Search Algorithm (MOGSA), Pareto Optimality, Indirect Niching
شبیه سازی مقاله
MOGSA, A Gravity Inspired Multi-Objective Meta-heuristic
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

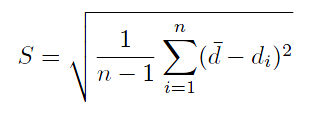
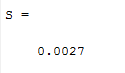
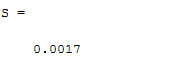

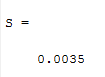
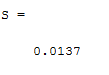
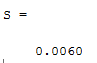


دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.