توضیحات
Modified input estimation technique for tracking manoeuvring targets
تکنیک تخمین ورودی اصلاح شده برای ردیابی اهداف مانور
قسمتی از گزارش شبیه سازی با متلب به همراه نتایج:
- فرض کنید T=1 پایداری سیستم را بررسی کنید.
حل: برای حل باید مقادیر ویژه ماتریس F را محاسبه کنیم.
اگر تمام مقادیر ویژه در دایره واحد بود سیستم پایدار است.
کد متلب زیر را که در بخش part12 نوشته شده است بدین منظور است.
(توضیحات مربوط به کلیه کدها به صورت کامنت در برنامه نوشته شده است و از توضیح کد در گزارش صرف نظر شده)
…
- اگر و Qii=1 وRii=10000 و g=9.8و با استفاده از شبیه سازی و حل معادلات حالت درایه های ماتریس کوواریانس حالت و خروجی را رسم کنید.
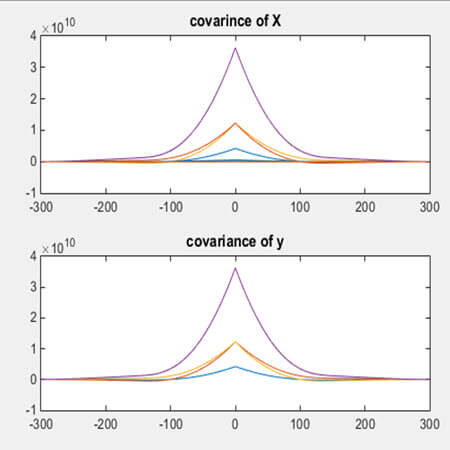
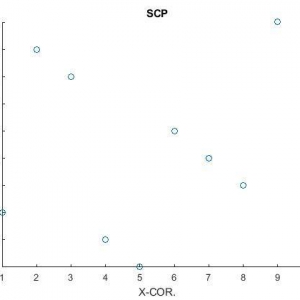
حل:کد زیر جهت حل معادله نوشته شده است و با محاسبه بردار x به محاسبه تابع همبستگی x و y میپردازیم. نتایج این قسمت در شکل شماره 1 نشان داده شده است.
StateDim = 4; % Number of states ( size(F,1) )
ObsDim = 2; % Number of observations ( size(H,1) )
…
شکل1- تابع هبستگی حالت ها و خروجی
- با توجه به اینکه تنها اطلاعات در دسترس موقعیت هدف در صفحه x-y است سرعت و شتاب را با اندازه گیری موقعیت تخمین زده و با مقادیر واقعی مقایسه کنید.
حل: در قسمت دوم با حل معادلات بردار X را به دست آوردیم . حال اگر فرض کنیم فقط xوy در دسترس هستند با توجه به اینکه سرعت مشتق اول مکان و شتاب مشتق دوم مکان است به تخمین سرعت و شتاب با توجه به رابطه های زیر میپردازیم
با نوشتن کد زیر در متلب((part3 با استفاده از فرمولهای بالا به تخمین مقدار سرعت در راستای محور x و yهمچنین تخمین شتاب در راستای محور x و y میپردازیم و با مقادیر واقعی که از حل معادله گسسته اولیه با شرایط اولیه معلوم به دست آمده اند مقایسه میکنیم.
StateDim = 4;
ObsDim = 2;
F = [1 1 0 0;0 1 0 0;0 0 1 1;0 0 0 1];
G=[0.5 1 0 0;0 0 0.5 1]’;
C=[1/2 1 0 0;0 0 1/2 1]’;
H = zeros(ObsDim,StateDim);
H(1,1) = 1; H(2,3)=1;
N = 300;
…
با اجرای کد بالا ، در شکل 2 نمودار مقادیر vx و مقادیر تخمین زده vx و همچنین مقادیر vy و تخمین زده vy رسم شده است.
شکل 2- نمودار سرعت در راستای محور x وy و مقادیر تخمین زده شده با روش تفاضل مرتبه اول
برای نشان دادن خطای این روش نمودار خطای سرعت در راستای محور x وy را به صورت جداگانه در شکل 3 رسم میکنیم.
شکل3 – نمودار خطای تخمین سرعت با روش تفاضل مرتبه اول
برای محاسبه شتاب دز راستای محور x و y از تفاضل مرتبه اول سرعت تخمین زده شده استفاده میکنیم.
که تخمین شتاب در شکل شماره 4 رسم شده است.
شکل 4- نمودار تخمین شتاب
- با استفاده از معادلات فیلتر کالمن بردار x را تخمین بزنید و با مقادیر واقعی مقایسه کنید.
با نوشتن کد زیر مراحل تخمین بردار X با فیلتر کالمن با ورودی معلوم اجرا میشود و در 300 مرحله به تخمین بردار X می پردازد.
clear
clc
close all
StateDim = 4; % Number of states ( size(F,1) )
ObsDim = 2; % Number of observations ( size(H,1) )
N = 300;
…
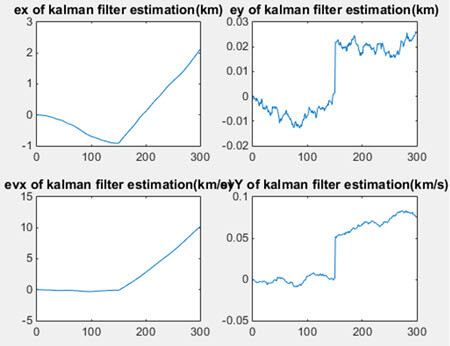
با اجرای کد بالا و رسم مقادیر X و y وvx وvy در شکل 5 و همچنین رسم نمودار خطای تخمین فیلتر (در مقیاس کیلومتر) در شکل 6 میبینیم که این فیلتر تخمینگر مناسبی برای تخمین حالت میباشد.
خطای تخمین در مقایسه با مقادیر بردار حالت بسیار ناچیز است.
شکل5- نمودار تخمین حالت با روش فیلتر کالمن
همانطور که در شکل بالا نشان داده شده است از لحظه اول تا 150 که مانور شتاب وجود ندارد حالتها تقریبا اطراف صفر هستند از لحظه 150 تا 300 با وجود ورودی معین مقادیر از صفر فاصله میگیرند
شکل6- نمودار خطای تخمین با روش فیلتر کالمن
- پایداری سیستم تخمین گر را بررسی و بحث نمایید
حل : برای بررسی پایداری تخمین گر بافرض داشتن واریانس در بی نهایت( در اینجا ماتریس واریانس در 300 را در نظر میگیریم) باید تمام مقادیر ویژه که به صورت زیر محاسبه میشود درون دایره واحد قرار گیرند.
K=Px*H’*inv(R);
Ftilda=(eye(4)-K*H)*F;
B=eig(Ftilda)
…
پس از اجرای برنامه بالا میبینیم که تمام مقادیر ویژه ماتریس درون دایره واحد قرار دارند پس تخمینگر پایدار است
0.9290 + 0.0662i
0.9290 – 0.0662i
0.9273 + 0.0677i
0.9273 – 0.0677i
- چنانچه از دو سنسور دیگر نیز استفاده کنیم، خواهیم داشت
…
با توجه به معادلات فیلتر کالمن بردار X را تخمین بزنید و با مقادیر قسمت 4 مقایسه کنید.
با اجرای مجدد فیلتر کالمن در حالی که تعداد مشاهدات به 4 افزایش پیدا کرده است و تغییر ماتریس H و ماتریس کوواریانس نویز تخمین بردار X را در شکل 7 مشاهده میکنیم.
شکل7 – تخمین بردار X با وجود 4 مشاهده
برای مقایسه با سوال 4 ابتدا باید خطای تخمین را رسم کنیم. این خطا در شکل شماره 8 رسم شده است.
شکل8- خطای تخمین بردار X با داشتن 4 مشاهده
برای مقایسه با حالتی که فقط دو مشاهده داشتیم در هر حالت به محاسبه میانگین مجذور خطا میپردازیم که نتایج در جدول 1 نوشته شده است.
|
خطا |
حالت 4 مشاهده | حالت 2 مشاهده |
|
میانگین مجذور خطا ex2 |
0.4842 |
3.4352 |
|
میانگین مجذور خطا evx2 |
8.2309e-04 |
1.7077e-04 |
|
میانگین مجذور خطا ey2 |
2.3317 |
8.0494 |
| میانگین مجذور خطا evy2 | 8.3703e-04 |
9.3003e-04 |
همانطور که از جدول بالا مشخص است در حالت 4 مشاهده خطا کمتر است
- در این قسمت هدف آن است که با استفاده از ماتریس افزوده و الگوریتم پیشنهادی در متن سوال به تخمین همزمان بردار X و ورودی u بپردازیم.
معادلات مربوط به این حالت را در متلب مینویسیم. در این مورد 6 حالت و 2 مشاهده داریم Faug ، Haug، Gaug را در کد تعریف کرده ایم .
clear
clc
close all
StateDim = 6; %number of states
ObsDim = 2; % Number of observations ( size(H,1) )
N = 300;
…
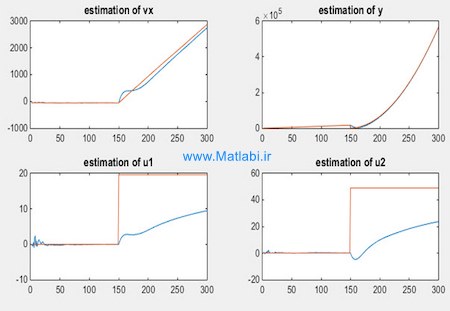
نتیجه تخمین با این روش در شکل زیر رسم شده است. همانطور که میبینیم نتیجه موجود با نتیجه موجود در مقاله متفاوت است و این تخمین گر قابلیت تخمین مناسب ورودی u شتاب را ندارد.
شکل10 – تخمین بردار X وu با روش الگوریتم 1
کلید واژه:
target tracking, Bayes methods, Kalman filters, Monte Carlo methods
شبیه سازی تکنیک تخمین ورودی اصلاح شده برای ردیابی اهداف مانور با متلب
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.









دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.