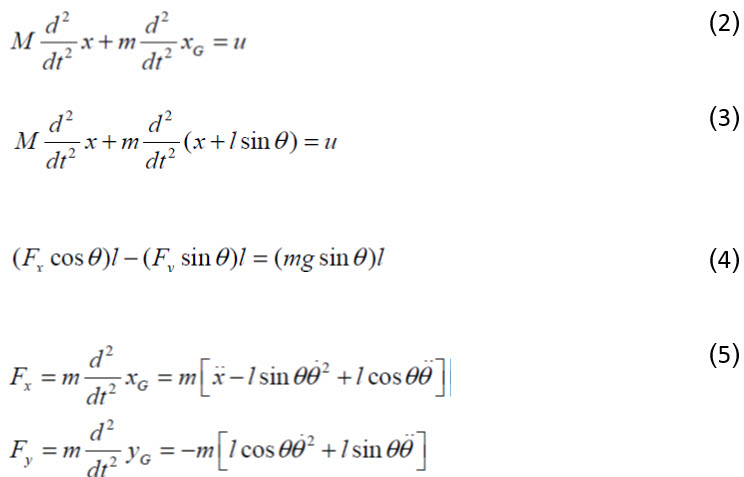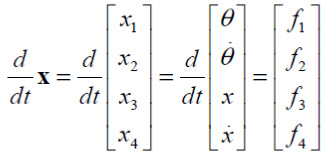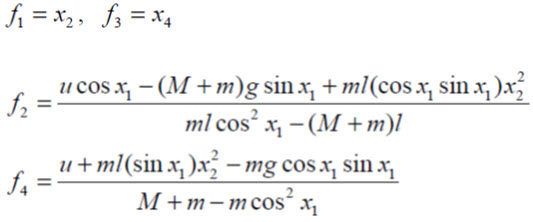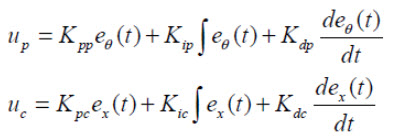توضیحات
Modelling & Simulation for Optimal Control of Nonlinear Inverted Pendulum Dynamical System using PID Controller & LQR
طراحی کنترل کننده LQR برای کنترل پاندول معکوس
مدل غیر خطی آونگ معکوس
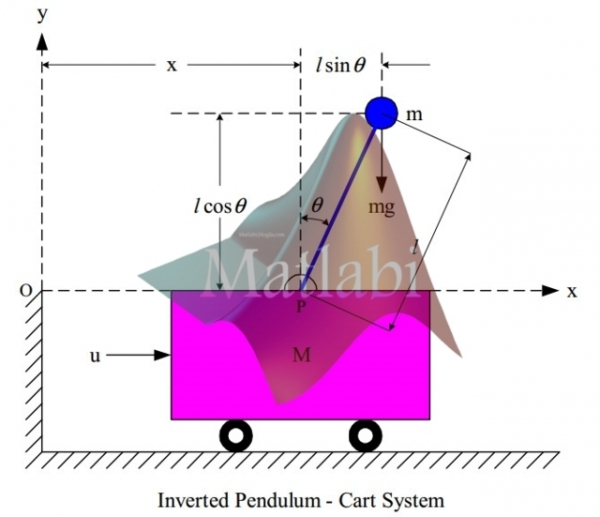
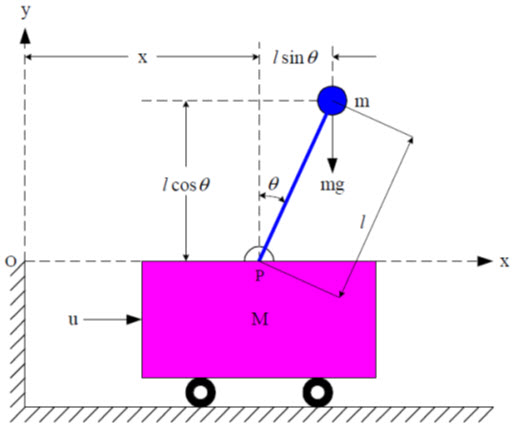
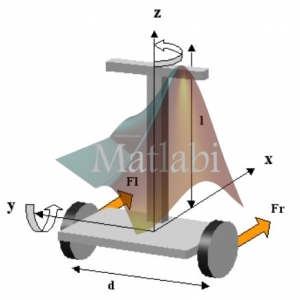
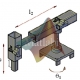
مطابق شکل 1 پاندول معکوس به جرم m و به طول l در نظر گرفته می شود که روی ارابه ای به جرم M می تواند حرکت افقی داشته باشد.
نیروی اعمالی F باعث حرکت ارابه و تعادل پاندول معکوس خواهد شد.در این مسئله فرض شده است که میله پاندول دارای جرم ناچیز می باشد و اصطکاک وجود ندارد.
شکل 1 – پاندول معکوس
اندازه موقعیت جسم (نامتغیر با زمان) به صورت زیر تعیین می شود:
(1)
با استفاده از قوانین فیزیکی و بکار گیری روابط بالا با استفاده از قانون بقای انرژی ، روابط به صورت زیر در امتداد x و θ بدست می آید.
معادله 6 با استفاده از رابطه 2 و 1 و3 و معادله 7 با ساده سازی معادلات 4 و 5 بدست می آیند که در واقع نشان دهنده معادلات حرکت سیستم غیر خطی می باشند.
با در نظر گرفتن متغیر های حالت به صورت زیر معادلات سیستم به فرم معادلات حات بدست می آیند.
(8)
معادلات حالت عبارتند از :
(9)
که در آن
(10)
در فایل سیمولینک معادلات غیرخطی در در بلاک subsystem شبیه سازی شده اند.
خطی سازی حول نقطه تعادل
خطی سازی به روش بسط سری تیلور، با توجه به معادله زیر در نقاط تعادل سیستم صورت می گیرد.
(11)
با در نظر گرفتن x0 = 0 و u = 0 معادلات خطی به صورت زیر تعریف می شوند :
A = [0 1 0 0; 29.8615 0 0 0; 0 0 0 1; -0.9401 0 0 0];
B = [0; -1.1574; 0; 0.4167];
C = [1 0 0 0; 0 0 1 0];
D = [0 0];
طراحی کنترلر PID
معادلات مربوط به PID به صورت زیر می باشند. ضرایب در این مسئله با روش آزمون و خطا تعیین می شوند.
(12)
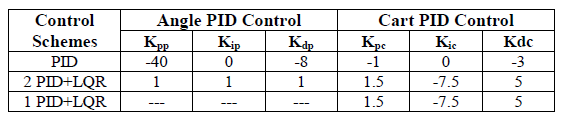
برای شکل های مختلف شبیه سازی و بکار گیری کنترلر ، ضرایب در جدول زیر نوشته شده است:
طراحی کنترلر LQR
کنترلر LQR با توجه به تابع معیار مشخص شده و حل معادله ریکاتی بدست آمده و با در نظر گرفتن مقادیر Q و R به صورت زیر طراحی می گردد.
(13)
(14)
Q = [1 0 0 0; 0 1 0 0; 0 0 500 0; 0 0 0 250];
R = 1;
ضرایب فیدبک بدست آمده به صورت زیر می باشد:
K = [-137.7896 -25.9783 -22.3607 -27.5768];
شبیه سازی :
….
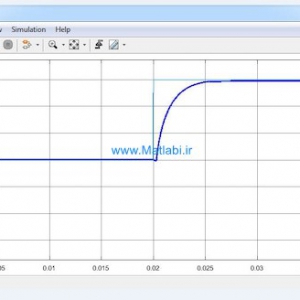
شکل 2 – شبیه سازی در حضور کنترلر PID
….
شکل 3 – شبیه سازی در حضور یک کنترلر PID و LQR
…
شکل 4 – شبیه سازی با کنترلر های PID و LQR
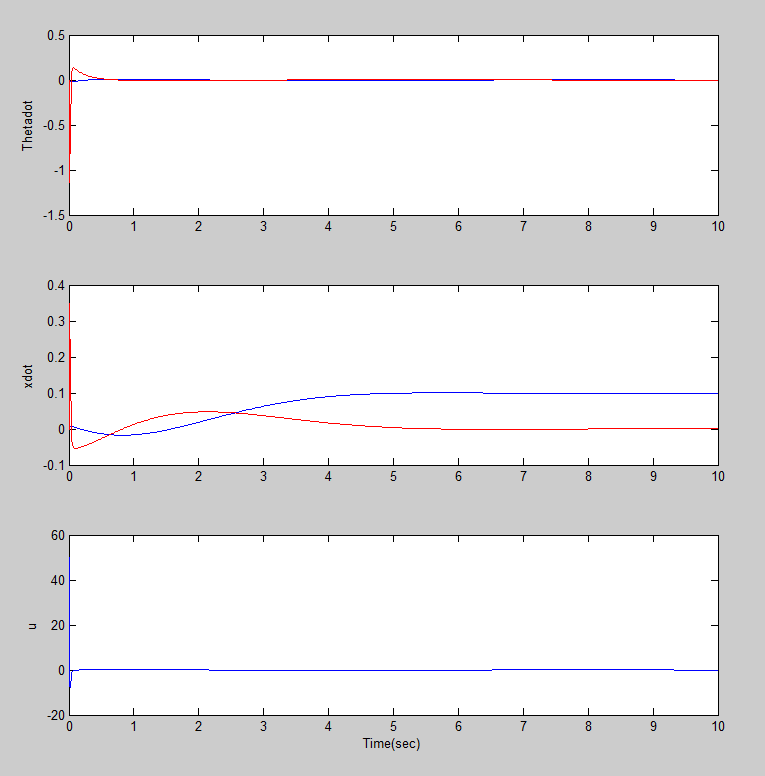
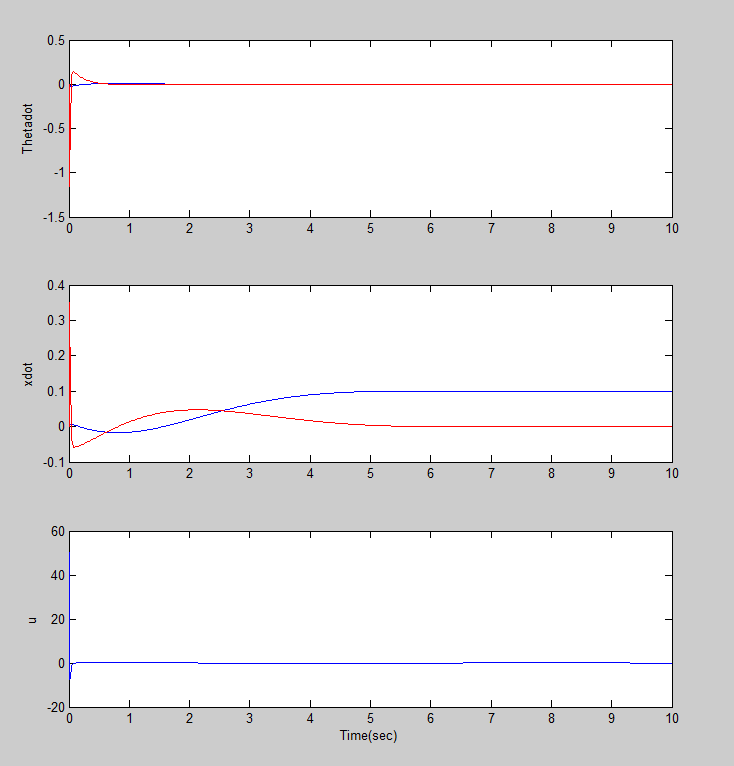
شکل 5 – خروجی و ورودی سیستم با کنترلر PID
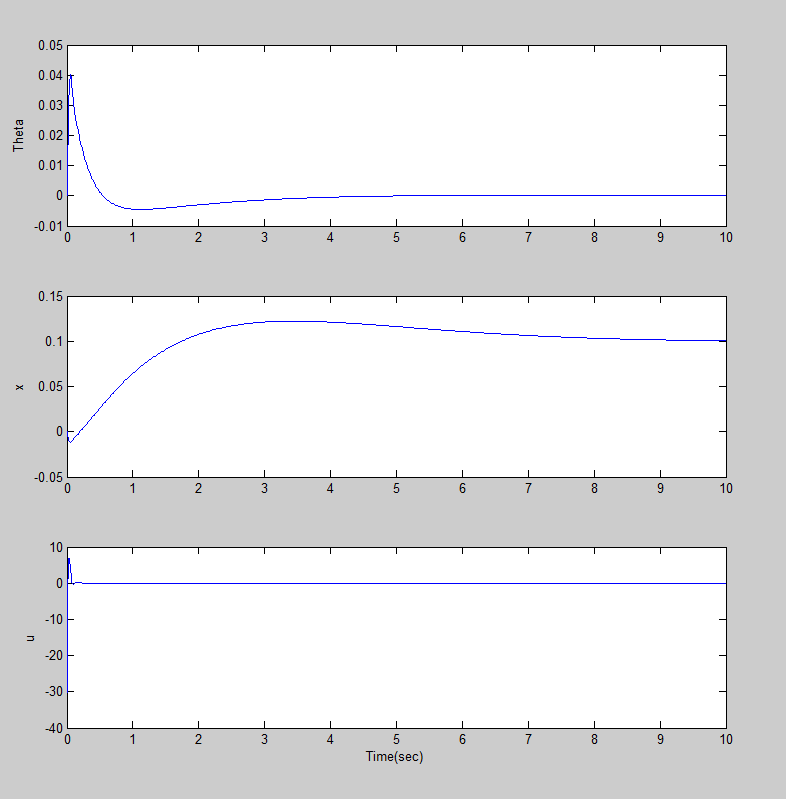
شکل 6 – خروجی و ورودی سیستم با کنترل LQR و یک PID
شکل 7 – خروجی و ورودی کنترلی سیستم با کنترل LQR و PID روی هردو خروجی
در این مقاله برای سیستم غیر خطی آونگ معکوس به طراحی کنترلر پرداختیم.
کنترلر بهینه به همراه کنترلر PID همانطور که ار نتایج مشخص می شود ، سبب بالاتر بردن کارایی و شاخص های کنترلی نسبت به استفاده مجزا از آنها در سیستم می شود.
جهت بهتر کردن سیستم کنترلی می توان به جای روش آزمون و خطا از روشهای هوشمند نیز جهت یافتن ضرایب PID در دو حلقه کنترلی، مانند الگوریتم ژنتیک یا الگوریتم PSO بهره برد.
Inverted pendulum, nonlinear system, PID control, optimal control, LQR , پروژه متلب, پروژه matlab , شبیه سازی با متلب
شبیه سازی
Modelling & Simulation for Optimal Control of Nonlinear Inverted Pendulum Dynamical System using PID Controller & LQR
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.