توضیحات
Modeling, Simulation, and Control of an Oil Heater
مدل سازی، شبیه سازی و کنترل یک گرم کننده نفتی
در توضیحات زیر بخش هایی با … پر شده است.
با خرید محصول نسخه کامل شبیه سازی و گزارش قابل دریافت است.
پروژه چند متغیره:
سيستم گرمکننده روغن
1- معرفی سیستم
1-1: مدل سیستم
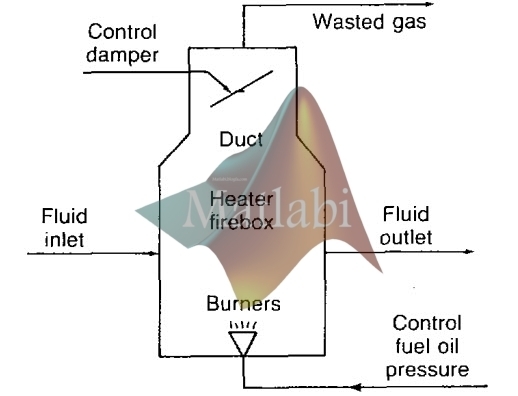
در شکل زیر دياگرام يک گرمکننده روغن نشان داده شده است. سيالي که بايد گرم شود روغني درحدود 320 درجه سانتيگراد ميباشد.
دماي سيال ورودي در حدود 285 درجه ميباشد.
دياگرام يک سيستم گرمکننده روغن
اين سيستم دو متغير کنترل شونده دارد که يکي فشار سوخت روغن و ديگري زاويه و جهت مجراي اکسیژن ميباشد.
اين دو متغير کنترلي براي کنترلکردن دماي سيال خروجي و درصد اکسيژن خارجشونده بهکار ميروند.
بنابراين سيستم مورد نظر يک سيستم چندمتغيره 2 -ورودي-2خروجي ميباشد. دو عمل مهم جهت سيستم کنترلي انجام ميشود.
اولين کار اين است که تا حد امکان دماي خروجي با نوسانات کم و پاسخ نسبتا سريع باشد.
در نقطه کار عادي، انحراف دماي خروجي نبايد بيشتر از باشد.
دومين کار اين است که درصد اکسيژن در مجرا را تا حد امکان کاهش دهيم، زيرا بازده گرمايي گرمکننده به ميزان اکسيژن بستگي دارد.
تحت شرايط مناسب، درصد پايينتر اکسيژن باعث بيشتر شدن بازده گرمايي ميشود.
نتايج آزمايشگاهي نشان ميدهد که انحراف فشار سوخت روغن تنها تاثير بر روی دماي خروجي ندارد بلکه بر روی فشار اکسيژن مجرا نيز تاثیر می گذارد.
هنگامي که فشار سوخت روغن پايين بيايد درصد اکسيژن افزايش يافته و بنابراين بازده گرمايي گرمکن پايين ميآيد
هنگامي که دمپر بسته ميباشد، درصد اکسيژن پايين ميآيد، اما باعث افزايش دماي خروجي ميشود.
بنابراين اندرکنشي قوي بين متغيرهاي کنترلي و هر سيگنال کنترل وجود دارد. انجام پروژه متلب با متلبی
بنابراين دو متغير ورودي فشار سوخت روغن ورودي P و جهت مجراي دمپر X و دو متغير خروجي کنترلي دماي سيال خروجي T و درصد اکسيژن مجرا O ميباشد.
Y(s)=G(s)U(S)
ماتريس 2*2 تابع تبديل G(s) که براي سيستم به دست آمده است در زير آورده شده است.
ابعاد همه متغيرها به ولت تبديل شده و مقياس زماني ثانيه ميباشد.
…
سيستم مورد نظر داراي 5 قطب حلقه باز پايدار ميباشد که 4 تاي آنها مزدوج ميباشند.
قطبهاي حلقه باز سيستم عبارتند از:i 0102/0+0177/0- و i0102/0-0177/0- و i0104/0+0150/0- و i0104/0-0150/0- و 0143/0- .
همچنين اين سيستم داراي دو صفر انتقال مزدوج ميباشد که در سمت چپ صفحه فرکانسي قرار دارند، بنابراين سيستم غيرمينيممفاز ميباشد.
اين صفرها عبارتند از
: i0104/0+0143/0- و i014/0-0143/0-
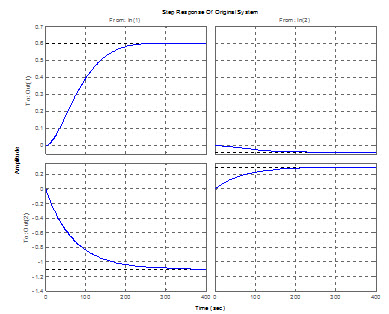
پاسخ پله سيستم حلقه باز:
پاسخ پله سيستم حلقه باز
در اين شكل واضح است كه تداخل در سيستم زياد بوده ولي سيستم پايدار است
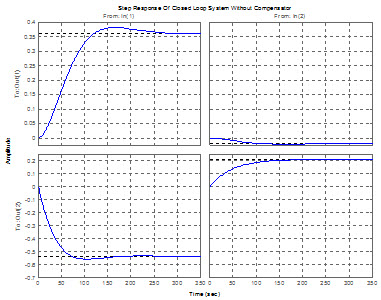
پاسخ پله سيستم حلقه بسته:
پاسخ پله سيستم با فيدبک واحد بدون جبرانساز
2- طراحي به روش Characteristic Loci
در طراحي کنترلكننده براي سيستمهاي چندمتغيره به دنبال هدفهای زير هستيم:
در حالت دائمي: در حالت دائمي بايد تا آنجا که امکان دارد خطاي حالت دائمي صفر شود و تداخل بين کانالها از بين برود. اگر تابع تبديل حلقه باز سيستم را به صورت زير تجزيه کنيم:
در اين صورت تابع تبديل حلقه بسته سيستم به شكل زير خواهد بود :
…
بنابراين مقادير ويژه سيستم حلقه بسته زير را خواهيم داشت :
…
بنابراين با توجه به اينکه مي باشد براي اينکه خروجي تقريبا ورودي را دنبال کند(خطاي حالت دائمي صفر) و از طرف ديگر داراي اندرکنش کمي باشد مي توان رابطه زير را نتيجه گرفت:
از طرفي با توجه به مقادير ويژه ارائه شده، براي اينکه تابع تبديل حلقه بسته ماتريس يکه شود خاصيت زير را مي توان براي مقادير ويژه تابع تبديل حلقه باز بدست آورد:
بنابراين هر چه اندازه مقادير ويژه سيستم حلقه باز در فرکانسهاي پايين (حالت دائمي) بزرگ باشد سيستم در حالت دائمي داراي خطاي حالت دائمي و اندرکنش کمي خواهد بود که در واقع همان مشخصات مطلوب طراح براي حالت دائمي مي باشد.
بهترين روش براي افزايش در فرکانسهاي استفاده از انتگرالگير مي باشد که در الگوريتم بيان شده در بخشهاي بعدي اين موضوع بيشتر مورد بررسي قرار مي گيرد.
حالت گذرا
در حالت گذار نيز به دنبال کاهش اندرکنش مابين کانالها مي باشيم.
بنابراين مي بايستي رابطه زير را داشته باشيم:
….
با توجه به اينکه رابطه …. براي سيستم حلقه بسته برقرار است در اينصورت خواهیم داشت :
…
بنابراين اگر ورودي به صورت به سيستم اعمال نماييم خروجي فقط در جهت iام حاکم خواهد بود و يا بعبارت ديگر اندرکنش بسيار ناچيز مي گردد.
پس مي بايستي بردارهاي ويژه را در جهت بردارهاي يکه انتخاب نماييم.
براي اندازه گيري زاويه بين بردارهاي ويژه و بردارهاي يکه از معيار Misalignment Angle استفاده مي کنيم که به صورت زير تعريف مي شود:
…
پس براي از بين بردن اندرکنش در فرکانسهاي بالا مي بايستي با طراحي کنترل کننده مناسب Miss Alignment Angle را از بين ببريم (…).
در روش characteristic loci نيز کنترل کننده را طوري طراحي مي کنيم که بتوانيم به اهداف مربوط به حالت گذراي و دائمي فوق دست يابيم.
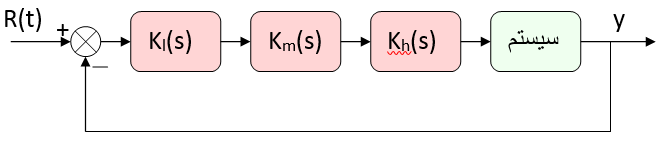
براي اين منظور براي سيستم با تابع تبديل حلقه باز G(s) کنترل کننده اي به صورت بلوک دياگرام زير طراحي مي کنيم:
ساختار كلي CL
2-2 – طراحي جبرانساز فرکانس بالا:
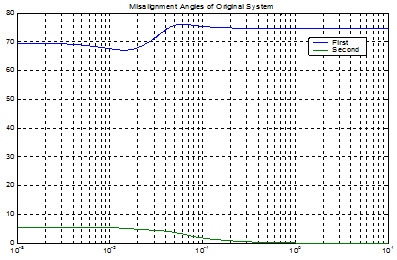
قبل از طراحی کنترلکننده در فرکانس بالا ابتدا میزان زاویه همراستایی را در شکل زیر مشاهده میکنید.
زاويه ناهمراستايي سيستم حلقه باز(جبراننشده)
همانطور که از شکل زیر مشاهده میشود زاویه ناهمراستایی در یکی از C.L.ها زیاد است که باعث اندرکنش زیاد در فرکانسهای بالا میشود.
به همین منظور با استفاده از یک جبرانساز در فرکانس بالا این اندر کنش را کم کرده و زاویه ناهمراستایی مربوط به این مقدار ویژه را کاهش میدهیم.
مرحله اول: طراحي در فرکانسهاي بالا
در اين مرحله هدف از طراحي آن است که تداخل موجود در سيستم بگونهاي باشد که باشد.
براي انجام طراحي مقدار فرکانس 1/0 در نظرگرفته شده است.
لذا با استفاده از الگوريتم Align کنترلکننده فرکانس بالا بصورت زير بدست ميآيد:
با توجه به اين طراحي، سيستم جبرانشده در فرکانس بالا بصورت زير است:
شکلهاي زیر به ترتیب بیانگر زاویه ناهمراستایی، دیاگرام بود و پاسخ پله سیستم حلقه بسته با فیدبک واحد بعد از جبران سازی در فرکانس بالا را نشان میدهد.
…
زاويه ناهمراستايي سيستم جبرانشده در فرکانس بالا
…
دیاگرام بود سيستم جبرانشده در فرکانس بالا
…
پاسخ پله سیستم جبران شده دز فرکانس بالا
مشاهده ميگردد که بواسطه استفاده از جبرانساز Align در فرکانسهاي بالا تداخل سيستم کمترشده است.
با توجه به شکل زیر میزان فزاجهش زیاد است.
2-3 – مرحله دوم: طراحي در فرکانسهاي مياني
همانطورکه پيشتر بيان شد، هدف از انجام طراحي در فرکانسهاي مياني بهبود عملکرد سيستم و بدست آوردن حدفاز و حدبهره مناسب براي پاسخ سيستم با استفاده از کنترلکنندههاي lead و lag است.
براي اين سيستم فرکانس 05/0 راديان بر ثانيه بعنوان فرکانس در نظر گرفته شدهاست.
با در نظر گرفتن اين فرکانس و با استفاده از الگوريتم Align ماتريسهاي A وB بصورت زير بدست ميآيند:
نيز که ماتريس قطري حاوي جبرانسازهاي lead و lag است با توجه به ملزومات طراحي بصورت زير بدست ميآيد:
همانطور که ملاحظه میکنید یکی از جبرانسازها پیشفاز و دیگری پسفاز انتخاب شده تا سرعت و فراجهش مناسب باشد.
شکل زیر دیاگرام بود سیستم جبران شده در فرکانس میانی را نشان میدهد.
نمودار بود C.L.هاي سيستم جبرانشده در فرکانس مياني
پاسخ پله سیستم جبران شده دز فرکانس میانی
لازم به ذکر است که طراحی جبرانساز در فرکانسهای میانی نباید لطمهای به جبران کننده در فرکانس بالا وارد کند.
در شکل زیر زاویه ناهمراستایی سیستم جبران شده در فرکانس میانی را مشاهده میکنید.
زاويه ناهمراستايي سيستم جبرانشده در فرکانسهاي مياني
2-4 – مرحله سوم: طراحي در فرکانسهاي پايين
در اين مرحله طراح سعي ميکند جبرانکننده فرکانس پايين که عموماً مانند جبرانساز فرکانس مياني يک ديناميک است را بگونهاي طراحي کندکه رفتار حالت ماندگار سيستم مطلوب باشد.
براي دستيابي به عملکرد مطلوب جبرانساز فرکانس پايين قطري بصورت زير طراحي ميگردد:
…
حال پس از طراحي سهمرحلهاي و با کنارهمقرارگرفتن جبرانسازهاي مختلف و بستن حلقه فيدبک واحد بصورت آرايش شکل زیر پاسخ حلقه بسته سيستم جبرانشده بصورت زير بدست ميآيد:
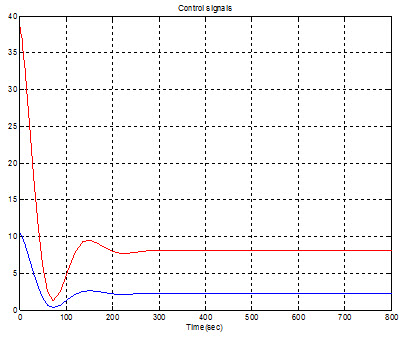
در شکل زیر سیگنال کنترلی که به سیستم اعمال میشود بازای این طراحی نشان داده شده است.
سیگنال کنترلی اعمالی به سیستم
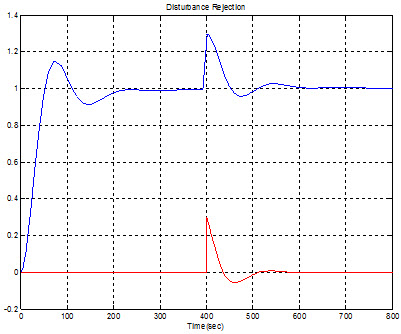
در این قسمت میخواهیم پاسخ سیستم به ورودی پله و در حضور اغتشاش را مورد بررسی قرار دهیم.
فرض میکنیم که در زمان t=400 ثانیه به سیستم یک اغتشاش وارد میشود.
در شکل زیر نمودار خروجی اول سیستم بازای اغتشاش 30٪ در خروجی دیده میشود.
حذف اثر اغتشاش
3: طراحي بهروش آرايه نايکوئيست
3-1: معرفی روش
براي طراحي بهروش آرايه نايکوئيست سيستم بايد حتماً مربعي باشد.
جبرانکنندههاي طراحي شده بايد معکوسپذير و تمام قطبها و صفرهاي آن بايد سمت چپ محور موهومي باشند.
قضيه: فرض کنيد جبرانکننده K(s) يک ماتريس مربعي و معکوسپذير باشد که تمام قطبها و صفرهاي آن سمت چپ محور موهومي باشند.
آنگاه همواره ميتوان K(s) را بفرم زير نوشت:
…
در اينجا يا ماتريسهاي پيش ضربکننده ميباشند که در واقع سطرها يا ستونها را جابجا ميکنند و از حاصلضرب ماتريسهاي مقدماتي بدست ميآيند.
يا حاصلضرب ماتريسهاي مقدماتي است که هريک از اين ماتريسهاي مقدماتي بصورت زير است:
که توابعي کسري و پايدار است و و iامين و j امين بردار اوليه هستند.
نهايتاً و ماتريسهاي قطري بفرم زير هستند:
توابعي کسري و غيرصفر هستند که تنها قطبها و صفرهاي سمت چپ محور موهومي دارند.
اين قضيه در واقع نشان ميدهد که طراحي جبرانکننده با استفاده از روش آرايههاي نايکوئيست در دو مرحله انجام ميپذيرد، که عبارتست از:
دو بند از گزارش در اینجا نیامده و با خرید این محصول قابل دریافت است.
3-2: طراحي براي سيستم گرمکننده روغن
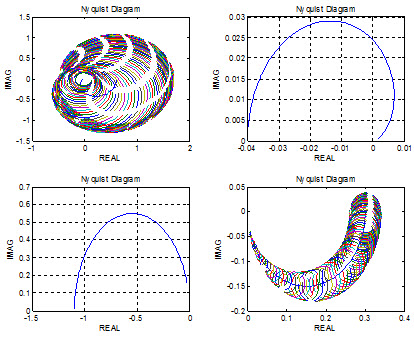
شکل های زیر نمايش باندهاي گرشگورين براي تابع تبديل حلقه باز و معکوس آن است.
در شكل دومی ديده ميشود كه تابع تبديل مستقيم DD است.
اما ديده ميشود كه تابع معكوس DD نيست و باندهاي گرشگورين نقطه را دربرگرفته است.
براي افزايش ميزان DD شدن تابع تبديل مستقيم بايد با استفاده از پيشجبرانساز مناسب استفاده كنيم.
اولين انتخاب، استفاده از معکوس تابع تبديل حلقه باز در يک فرکانس صفر است.
بنابراين پيشجبران ساز به صورت زير است.
باندهاي گرشگورين سيستم حلقه باز
باندهاي گرشگورين معکوس تابع تبديل حلقه باز
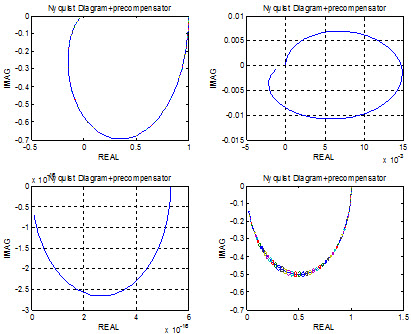
در شکلهاي زیر باندهاي گرشگورين سيستم حلقه باز با در نظر گرفتن پيشجبران ساز رسم شده است.
باندهاي گرشگورين سيستم حلقه باز در سيستم با پيش جبران ساز
باندهاي گرشگورين معکوس تابع تبديل حلقه باز در سيستم با پيش جبران ساز
با توجه به نمودارهاي بالا ديده ميشود که سيستم با پيش جبرانساز گفته شده DD تر ميشود.
با DD شدن سيستم کافي است به طراحي کنترلکننده بپردازيم.
در واقع در اينجا با دو سيستم تکورودي- تکخروجي که همان توابع تبديل روي قطر اصلي ماتريس تابع تبديل هستند کار ميکنيم.
طراحي درايههاي ماتريس قطري نيز با توجه به خواستههاي کنترلي تعريف شده براي عملکرد سيستم از جمله زمان نشست، زمان صعود، حداکثر خطاي حالت ماندگار و … انجام ميپذيرد.
با توجه به خواستههاي عملکردي مورد نياز کنترلکنندههاي زير طراحي شدهاند:
شکلهاي زیر به ترتيب پاسخ سيستم حلقه بسته و سيگنال کنترلي با استفاده از روش مستقيم آرايه نايکوئيست براي طراحي کنترلکننده سيستم گرمکننده روغن را نشان ميدهند.
پاسخ حلقه بسته سيستم جبران شده
سيگنال کنترلي براي پاسخ پله در سيستم جبران شده
در شکل زیر توانايي حذف اثر اغتشاش ديده ميشود.
در لحظه t=500 اغتشاشي با دامنه 3/0 به سيستم اعمال شده است.
توانايي دفع اثر اغتشاش کنترلکننده
4- طراحي كنترلكننده چند متغيره با استفاده از LQG/LTR
4-1: مقدمه
این روش يک روش طراحي مبتني بر تئوري کنترل بهينه مي باشد که شاخصترين تئوري که در آن به کار گرفته ميشود، حل مساله LQG يعني تخمين حالتها به کمک تخمين زننده بهينه فيلتر کالمن و طراحي رگولاتور بهينه خواهد بود.
همانطور که مي دانيم، هم رگولاتور LQ و هم فيلتر کالمن علمکرد و مقاوم بودن خوبي دارند، بنابراين انتظار مي رود کنترل کننده LQG هم خواص خوبي داشته باشد.
ولي در حالت کلي اينگونه نيست.
در واقع دو روش براي طراحي LQG داريم.
يا بهره فيدبک را قبل از طراحي فيلتر کالمن طراحي مي کنيم يا ابتدا يک فيلتر مي سازيم و بعد بهره فيدبک را ايجاد مي کنيم.
اگر دو روش مختلف از طراحي LQG را به کار بريم به دو نوع راه حل متفاوت مي رسيم.
به منظور پايدار سازي و رسيدن به عملکرد مطلوب يک راه انتخاب مقادير ويژه فيلتر کالمن در محل صفرهاي سيستم مي باشد.
در اين روش امکان شکل دهي بهره هاي اساسي نرخ بازگشت در خروجي يا ورودي سيستم به طراح داده مي شود تا به اين وسيله بتوان به مشخصات عملکردي مطلوب و مقاوم بودن مناسب دست پيدا کرد.
از مزاياي اين روش اين است که ذاتا پايدار ميباشد.
بنابراين نگران مشخصه هاي فاز نخواهيم بود.
دراين روش ابتدا با طراحي يک فيلتر کالمن و سپس رگولاتور بهينه در قالب مسأله LQG به شرايط مطلوب کنترلي دست پيدا مي کنيم.
سپس بااستفاده از تکنيک LTR حلقه را در خروجي بازيابي مي کنيم.
ابتدا به توضيح مختصري از تئوري LQG/ LTR مي پردازيم و سپس مراحل طراحي را براي سيستم مذکور بيان کرده و نتايج شبيه سازي را ارائه خواهيم کرد.
شکل زیر بلوک دیاگرام ساختار LQG با دو محل بازیابی حلقه را نشان میدهد.
| … |
| ساختار جبرانساز LQG با دو محل بازیابی حلقه |
4-2: معرفی روش طراحی LQG/LTR
این بخش اینجا قابل نمایش نیست و با خرید محصول قابل دریافت است.
4-3: طراحي فيلتر کالمن
مرحله اول طراحي فيلتر کالمن مي باشد.
طراحي اين قسمت شامل يافتن يک بهره KF است که متناسب با آن خطاي خروجي از مقدار تخمين زده شده در تخين حالت تاثير داده مي شود بطوريکه کوواريانس خطاي حالت از مقدار تخمين زده شده حداقل گردد.
از تابع Kalman در نرم افزار MATALB استفاده مي کنيم که سيستم اوليه و واريانس نويزهاي موثر در حالات و خروجي سيستم را بعنوان ورودي دريافت کرده و بهره Kf و کوواريانس خطاي تخمين حالت را بعنوان خروجي توليد مي نمايد.
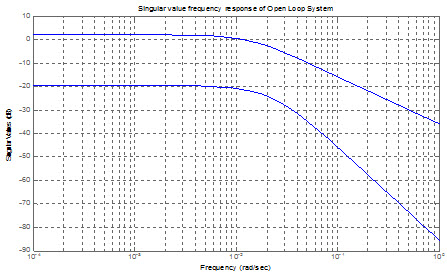
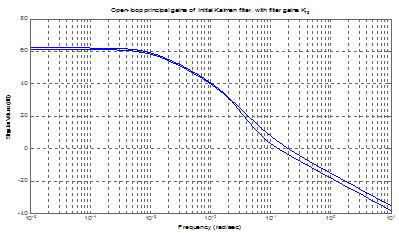
شکل زیر بيانگر بهرههاي اساسي[1] سيستم حلقه باز است.
بهرههاي اساسي سيستم حلقه باز
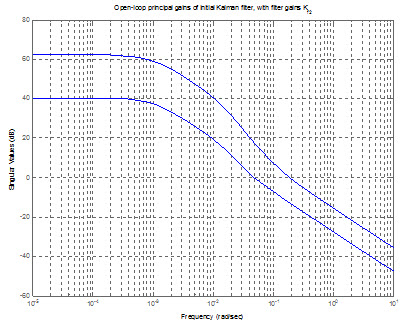
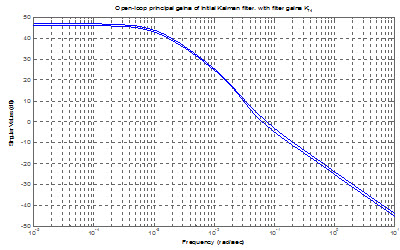
شکل زیر نمايش بهرههاي اساسي فيلتر کالمن يعني پس از اولين طراحي براي بهره كالمن است.
همانطورکه مشاهده ميشود بهرههاي اساسي سيستم در فرکانسهاي پايين مقادير بسيار کوچکي دارند.
يکي از اين بهرهها در حدود dB 4- و ديگري dB 37- است.
بدين ترتيب لزوم وجود يک انتگرلگير کاملا احساس ميشود.
براي بهبود طراحي يک انتگرالگير را در فرکانسهاي پايين به سيستم اضافه ميکنيم.
بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf1
از آنجايي که اضافه کردن انتگرالگير در فرکانس صفر در مرحله LTR مشکل ايجاد ميکند، انتگرالگير در فرکانس بسيار پايين که نزديک به صفر باشد مثلاً 0001/0 هرتز به سيستم اضافه ميشود.
شکل زیر نمايش بهرههاي اساسي سيستم فيلتر کالمن پس از اضافه کردن انتگرالگير را نشان ميدهد.
ديده ميشود که با افزايش انتگرلگير ميزان بهرهها در فرکانسهاي پايين dB 62 و dB 40 ميباشد که بوضوح افزايش يافته است.
همچنين بدليل قرار نگرفتن قطب انتگرالگير در مبدا شيب بهرههاي اساسي در فرکانسهاي پايين نهايتا صفر شده و بهره dc بينهايت نخواهد شد.
بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf2
حال به منظور افزايش سرعت کاهش خطاي حالت ماندگار بايد کوچکترين بهره اساسي (PG) را افزايش دهيم به گونهاي که اندازه آن در فرکانس پايين تقريبا برابر با اندازه بزرگترين PG گردد.
براي اين کار بايد کوچکترين بهره را در فرکانس پايين به ميزان dB 22 افزايش دهيم.
شکل زیر نشان ميدهد که بهره جديد فيلتر کالمن اين خواسته را برآورده کرده است.
بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf3
در گام چهارم طراحي فيلتر کالمن، توجه خود را به تغيير پهناي باند سيستم معطوف ميکنيم.
براي رسيدن به پهناي باند حدود 1/0 راديان بر ثانيه بايد بهرههاي اساسي را در حدود dB 5 کاهش داد.
با تغيير ضريب ماتريس W و محاسبه بهرههاي جديد بر اساس بهره کالمن Kf4 نمودار بهرههاي اساسي به شکل زیر در ميآيد.
بهرههاي اساسي حلقه باز براي فيلتر کالمن با بهره Kf4
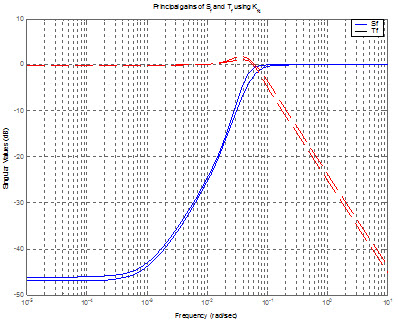
به منظور بررسي بيشتر و دستيابي به بهترين عملکرد براي فيلتر کالمن در ادامه به بررسي بهرههاي اساسي توابع حساسيت و متمم حساسيت (تابع تبديل حلقه بسته) فيلتر کالمن ميپردازيم.
در شکل زیر اين بهرهها رسم شدهاند.
با توجه به اينکه در حوالي فرکانس گذر از 0 dB بهرهها يکسان هستند، لذا طراحي توسط فيلتر کالمن در اين قسمت خاتمه پيدا کرده و بهره نهايي فيلتر کالمن که همان Kf4 است را در ادامه طراحي لحاظ ميکنيم.
در ادامه به فاز دوم طراحي يعني بازيابي حلقه خواهيم پرداخت.
بهرههاي اساسي تابع حساسيت و تابع تبديل حلقه بسته فيلتر کالمن با استفاده از بهره Kf4
4-4-: بازيابي حلقه
پس از طراحي فيلتر کالمن براي تخمين حالات سيستم، نوبت به طراحي يک رگولاتور مناسب براي سيستم ميشود.
جبرانسازهاي LQG عموماً عملکرد و مقاومت[2] خوبي دارند.
براي طراحي يک رگولاتور بايد ضرايب تابع هزينه را تا دستيابي به عملکرد مورد نظر تغيير دهيم.
براي طراحي رگولاتور مناسب دو روش بکاربرده ميشود.
4-4-1- بازيابي حلقه در ورودي
1. پس از تعيين ماتريسهاي وزني R و Q ، يک طراحي مناسب براي ماتريس بهره و مساله تنظيمکننده خطي بهينه(LQR) انجام ميدهيم بطوريکه مقاديراستثنايي بهره حلقه در ورودي سيستم يعني… داراي فرم مناسبي بوده و ملزومات طراحي را برآورده نمايد.
2. با قرار دادن و افزايش q و يا کاهش
را با حل مساله فيلتر کالمن چنان تعيين ميکنيم تا بهره حلقه در ورودي سيستم به بهره
در رنج نسبتاً وسيعي از فرکانسها منطبق گردد.
4-4-2- بازيابي حلقه در خروجي
اين روش دقيقاً دوگان روش بازيابي حلقه در ورودي است.
اين روش نيز بطورخلاصه در دو قدم بصورت زير است:
1. با تعيين ماتريسهاي کوواريانس V وW ، يک طراحي مناسب براي ماتريس بهره فيلتر و مساله تخمينگر بهينه حالت(KF) انجام ميدهيم بطوريکه مقادير استثنايي بهره حلقه در خروجي سيستم يعني … داراي فرم مناسبي بوده و ملزومات طراحي را برآورده نمايد.
2. این قسمت در گزارش کار آمده و اینجا منتشر نشده است.
شکل زیر نمايش بهرههاي اساسي به ازاي مقادير مختلف ميباشد.
همانطور که ديده ميشود به ازاي عملکرد سيستم بسيار مناسب است.
بازيابي بهرههاي اساسي حلقه باز به ازاي مقادير مختلف
در نهايت کنترل کننده نهايي بر اساس بهره فيلتر کالمن و بهره رگولاتور بصورت زير در ميآيد.
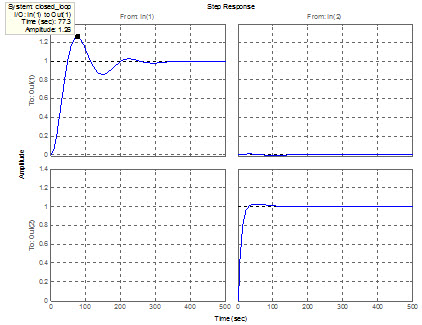
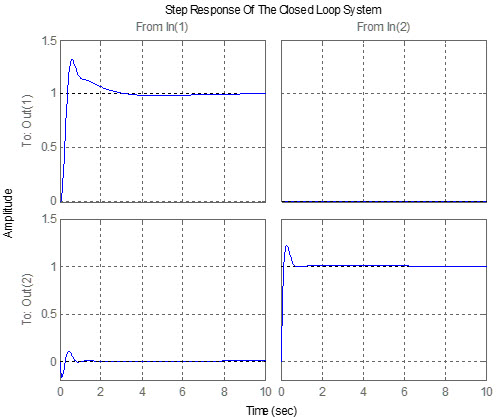
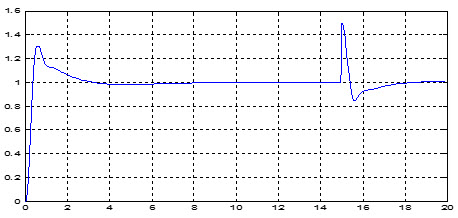
شکل زیر پاسخ پله سيستم حلقه بسته را با توجه به طراحي انجام شده براي بهره تخمينگر حالت(فيلتر کالمن) و رگولاتور بهينه با بستن حلقه فيدبک، نشان ميدهد.
همانگونه که ديده ميشود پاسخ حلقه بسته بسيار مطلوب بوده يعني اندرکنش بسيار کم و خطاي حالت ماندگار نيز مقدار کمي دارد.
شکل دومی شبیه سازی سیستم همراه با کنترلر طراحی شده را نشان می دهد.
پاسخ حلقه بسته پس از انجام طراحي
……
شبیه سازی سیستم همراه با کنترلر
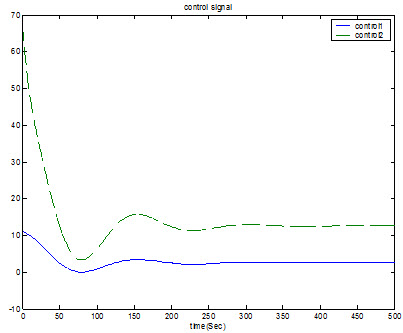
سيگنال کنترلي اعمالي به سيستم بازاي ورودي پله سيگنال مرجع
سيگنال کنترلي اعمالي به سيستم را نشان ميدهد که بازاي ورودي پله سيگنال مرجع بدست آمده است.
در شکل زیر عملکرد کنترلکننده در برابر اثر اغتشاش باري ثابت 4/0 و در لحظه t=15ثانيه ديده ميشود.
همانطور که از اين نمودار مشخص است کنترلکننده به خوبي اثر اغتشاش را از بين ميبرد.
توانایی دفع اثر اغتشاش
در شکل زیر توانايي کنترلکننده در خنثي کردن اثر نويز با توان 001/0 نشان داده شده است.
سيگنال خروجي آلوده به نويز و خنثيکردن آن توسط کنترل کننده طراحي شده
همانطور كه ديده ميشود اين روش نسبت به دو روش ديگر عملكرد بهتري در خنثي كردن اثر نويز دارد.
البته اين انتظار هم وجود داشت و دليل آن طراحي مقاوم اين روش و در نظر گرفتن نويز پروسه و اندازه گيري در هنگام طراحي است.
- Design and Simulation of Control Systems for a Field Survey Mobile Robot Platform
- کنترل مقاوم یک ستون تقطیر
مراجع:
[1] J. M. Maciejowski, Multivariable Feedback Design, Addison-Wesley, 1989.
[2] H. Zhuang, F. Bai and J. Xue, “Modeling, Simulation and Control of an Oil Heater, ” IEEE Control System Magazine, Vol. 7, No. 4, pp. 41-44, Aug 1987.
کلید واژه : کنترل چند متغیره, سيستم گرمکننده روغن,
طراحي به روش Characteristic Loci, آرايه نايکوئيست و LQG/LTR,
MIMO, LTR,LQG, Nyquist
شبیه سازی
Modeling, Simulation, and Control of an Oil Heater
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.


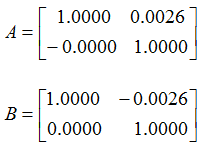
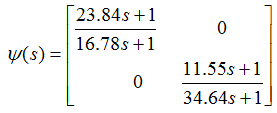



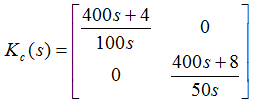







دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.