توضیحات
Haar wavelet method for nonlinear integro-differential equations
ابتدا پایه های هار ساخته می شود و با توجه به ماتریس عملیاتی انتگرال و معادلات داده شده در مقاله حل می شود
روش موجک Haar برای معادلات انتگرالی-دیفرانسیلی
برای محاسبه ماتریسهای H, Q در سیستم موجک Haar، برنامهای با نام HaarWavelet.m نوشته شده است.
ورودی تابع HaarWavelet مقدار J است (level) و خروجیهای آن ماتریسهای H, Q هستند.
روابط استفاده شده در این تابع، همان روابط ارائه شده در بخش 2 مقاله مرجع است.
به عنوان نمونهای از نتایج، اجرای دستور [H, Q]=HaarWavelet(1) در پنجره دستور MATLAB منجر به نتایج زیر میشود:
>> [H, Q] = HaarWavelet(1)
H =
1 1 1 1
1 1 -1 -1
1 -1 0 0
0 0 1 -1
Q =
0.1250 0.3750 0.6250 0.8750
0.1250 0.3750 0.3750 0.1250
0.1250 0.1250 0 0
0 0 0.1250 0.1250
>>
تابع HaarWavelet در جای لازم در برنامه اصلی با توجه به سطح مورد نظر (J=0, 1, 2, …, 6) فراخوانی میشود.
برای حل مثالهای موجود در مقاله مرجع، برنامههای Case1.m، Case2.m و Case3.m نوشته شده است که به ترتیب مربوط به Example 6.1، Example 6.2 و Example 6.3 در مقاله مرجع هستند.
ساختار کلی هر سه برنامه مشابه یکدیگر است و تنها در تعریف مشخصات مربوط به هر مسئله متفاوت هستند.
هر برنامه دارای یک حلقه خارجی برای مقادیر مختلف J است. در برنامه Case1.m :
…
در هر مقدار J، یک الگوریتم حدس و خطا برای محاسبه ضرایب موجک وجود دارد. الگوریتم بر اساس بخشهای 3 و 4 مقاله مرجع (Calculation of wavelet coefficients) نوشته شده است که از روش نیوتن برای محاسبه ضرایب کمک میگیرد. در برنامه Case1.m :
محاسبات تخمین خطا و همگرایی بر اساس بخش 5 مقاله مرجع (Error Estimates) نوشته شده است. در برنامه Case1.m :
نتایج شبیه سازی با متلب
نتایج اجرای برنامه Case1.m به صورت زیر است (ممکن است اجرای برنامه برای مقادیر بالاتر J، با توجه به مشخصات پردازنده سیستم، کمی طول بکشد).
در هر سطح J، مقادیر u در نقاط x محاسبه شده توسط روش عددی با مقادیر تحلیلی دقیق u_ex مقایسه شدهاند.
———— Calculating for J = 0 —————-
x = 0.25 0.75
u = 0.26176 0.78654
u_ex = 0.25 0.75
eps = 0.036539
———— Calculating for J = 1 —————-
x = 0.125 0.375 0.625 0.875
u = 0.12634 0.37903 0.63183 0.88495
u_ex = 0.125 0.375 0.625 0.875
eps = 0.009948
rho = 3.673
delta= 0.036823
sigma= 27.1572
———— Calculating for J = 2 —————-
x = 0.0625 0.1875 0.3125 0.4375 0.5625 …
u = 0.062664 0.18799 0.31332 0.43865 0.564 …
u_ex = 0.0625 0.1875 0.3125 0.4375 0.5625 …
eps = 0.0026391
rho = 3.7694
delta= 0.0083374
sigma= 4.4166
———— Calculating for J = 3 —————-
x = 0.03125 0.09375 0.15625 0.21875 0.28125 …
u = 0.03127 0.093811 0.15635 0.21889 0.28143 …
u_ex = 0.03125 0.09375 0.15625 0.21875 0.28125 …
eps = 0.00068294
rho = 3.8644
delta= 0.0020367
sigma= 4.0936
———— Calculating for J = 4 —————-
x = 0.015625 0.046875 0.078125 0.10938 0.14063 …
u = 0.015628 0.046883 0.078138 0.10939 0.14065 …
u_ex = 0.015625 0.046875 0.078125 0.10938 0.14063 …
eps = 0.00017358
rho = 3.9343
delta= 0.00050649
sigma= 4.0212
———— Calculating for J = 5 —————-
x = 0.0078125 0.023438 0.039063 0.054688 0.070313 …
u = 0.0078128 0.023438 0.039064 0.05469 0.070315 …
u_ex = 0.0078125 0.023438 0.039063 0.054688 0.070313 …
eps = 4.3514e-05
rho = 3.9892
delta= 0.00012645
sigma= 4.0056
———— Calculating for J = 6 —————-
x = 0.0039063 0.011719 0.019531 0.027344 0.035156 …
u = 0.0039063 0.011719 0.019531 0.027344 0.035157 …
u_ex = 0.0039063 0.011719 0.019531 0.027344 0.035156 …
eps = 1.0632e-05
rho = 4.0925
delta= 3.1601e-05
sigma= 4.0014
همان طور که از مقایسه مقادیر u با u_ex مشخص است، حل عددی تطابق قابل قبولی با حل دقیق تحلیلی دارد. با توجه به نتایج بالا، جدول زیر حاصل میشود:
| 0 | 3.7E-02 | |||
| 1 | 9.9E-03 | 3.7 | 3.7E-02 | 27.2 |
| 2 | 2.6E-03 | 3.8 | 8.3E-03 | 4.4 |
| 3 | 6.8E-04 | 3.9 | 2.0E-03 | 4.1 |
| 4 | 1.7E-04 | 3.9 | 5.1E-04 | 4.0 |
| 5 | 4.4E-05 | 4.0 | 1.3E-04 | 4.0 |
| 6 | 1.1E-05 | 4.1 | 3.2E-05 | 4.0 |
همانطور که مشاهده میشود، روند نتایج و اندازه بزرگی پارامترهای حاصل شده مشابه است.
اختلاف بین مقادیر محاسبه شده توسط برنامه با مقادیر ارائه شده در جدول 1 مقاله مرجع ناشی از اختلاف در دقت حل ضرایب موجک و مواردی از این دست است.
نتایج اجرای برنامه Case2.m به صورت زیر است:
———— Calculating for J = 0 —————-
x = 0.25 0.75
u = 0.1237 0.34464
u_ex = 0.12403 0.34924
eps = 0.0045987
———— Calculating for J = 1 —————-
x = 0.125 0.375 0.625 0.875
u = 0.062337 0.18362 0.29541 0.39259
u_ex = 0.062378 0.18422 0.29749 0.39694
eps = 0.0043543
rho = 1.0561
delta= 0.0029273
sigma= 341.6075
———— Calculating for J = 2 —————-
x = 0.0625 0.1875 0.3125 0.4375 0.5625 …
u = 0.03123 0.093263 0.15408 0.21298 0.26928 …
u_ex = 0.031235 0.093339 0.15435 0.21356 0.27027 …
eps = 0.0028331
rho = 1.5369
delta= 0.0016111
sigma= 1.817
———— Calculating for J = 3 —————-
x = 0.03125 0.09375 0.15625 0.21875 0.28125 …
u = 0.015622 0.046814 0.077853 0.10865 0.13911 …
u_ex = 0.015623 0.046824 0.077887 0.10872 0.13924 …
eps = 0.0015995
rho = 1.7713
delta= 0.0016803
sigma= 0.95882
———— Calculating for J = 4 —————-
x = 0.015625 0.046875 0.078125 0.10938 0.14063 …
u = 0.0078122 0.02343 0.039028 0.054597 0.070123 …
u_ex = 0.0078123 0.023431 0.039033 0.054606 0.070139 …
eps = 0.00084789
rho = 1.8864
delta= 0.001074
sigma= 1.5645
———— Calculating for J = 5 —————-
x = 0.0078125 0.023438 0.039063 0.054688 0.070313 …
u = 0.0039062 0.011718 0.019527 0.027332 0.035133 …
u_ex = 0.0039062 0.011718 0.019528 0.027334 0.035135 …
eps = 0.0004363
rho = 1.9434
delta= 0.00059744
sigma= 1.7977
———— Calculating for J = 6 —————-
x = 0.0039063 0.011719 0.019531 0.027344 0.035156 …
u = 0.0019531 0.0058593 0.0097651 0.01367 0.017575 …
u_ex = 0.0019531 0.0058593 0.0097652 0.013671 0.017575 …
eps = 0.00022129
rho = 1.9716
delta= 0.00031409
sigma= 1.9021
همان طور که از مقایسه مقادیر u با u_ex مشخص است، حل عددی تطابق قابل قبولی با حل دقیق تحلیلی دارد. با توجه به نتایج بالا، جدول زیر حاصل میشود:
| 0 | 4.6E-03 | |||
| 1 | 4.4E-03 | 1.1 | 2.9E-03 | 341.6 |
| 2 | 2.8E-03 | 1.5 | 1.6E-03 | 1.8 |
| 3 | 1.6E-03 | 1.8 | 1.7E-03 | 1.0 |
| 4 | 8.5E-04 | 1.9 | 1.1E-03 | 1.6 |
| 5 | 4.4E-04 | 1.9 | 6.0E-04 | 1.8 |
| 6 | 2.2E-04 | 2.0 | 3.1E-04 | 1.9 |
نتایج اجرای برنامه Case3.m به صورت زیر است:
———— Calculating for J = 0 —————-
x = 0.25 0.75
u = 0.26795 0.90545
u_ex = 0.25264 0.82924
eps = 0.076207
———— Calculating for J = 1 —————-
x = 0.125 0.375 0.625 0.875
u = 0.23047 0.50043 0.60043 0.92496
u_ex = 0.12533 0.38404 0.66914 1.0069
eps = 0.11639
rho = 0.65478
delta= 0.040112
sigma= 24.93
———— Calculating for J = 2 —————-
x = 0.0625 0.1875 0.3125 0.4375 0.5625 …
u = 0.17169 0.38704 0.42806 0.47905 0.60006 …
u_ex = 0.062541 0.18861 0.31769 0.45201 0.59417 …
eps = 0.19843
rho = 0.58653
delta= 0.020114
sigma= 1.9942
———— Calculating for J = 3 —————-
x = 0.03125 0.09375 0.15625 0.21875 0.28125 …
u = 0.1171 0.28027 0.34005 0.38611 0.43873 …
u_ex = 0.031255 0.093888 0.15689 0.22051 0.28502 …
eps = 0.22249
rho = 0.89185
delta= 0.012433
sigma= 1.6179
———— Calculating for J = 4 —————-
x = 0.015625 0.046875 0.078125 0.10938 0.14063 …
u = 0.074925 0.18766 0.24516 0.29165 0.33625 …
u_ex = 0.015626 0.046892 0.078205 0.10959 0.14109 …
eps = 0.22064
rho = 1.0084
delta= 0.0070307
sigma= 1.7683
———— Calculating for J = 5 —————-
x = 0.0078125 0.023438 0.039063 0.054688 0.070313 …
u = 0.045878 0.11869 0.16305 0.20092 0.23672 …
u_ex = 0.0078126 0.02344 0.039072 0.054715 0.07037 …
eps = 0.22927
rho = 0.96239
delta= 0.0036465
sigma= 1.9281
———— Calculating for J = 6 —————-
x = 0.0039063 0.011719 0.019531 0.027344 0.035156 …
u = 0.027217 0.072082 0.10252 0.12947 0.15511 …
u_ex = 0.0039063 0.011719 0.019532 0.027347 0.03516 …
eps = 0.23554
rho = 0.97337
delta= 0.0018173
sigma= 2.0065
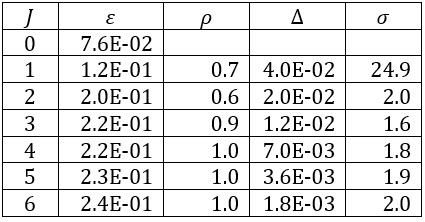
همانطور که مشاهده میشود، خطای محاسبات برای این مثال بالا است و نتایج جدول زیر اختلاف بسیار زیادی با مقادیر ارائه شده در مقاله مرجع دارند.
روند کلی برنامه کاملاً مشابه دو مثال قبلی است، اما نتایج در این مثال با مقاله همخوانی ندارد.
این عدم تطابق نتایج، احتمالاً ناشی از وجود اشتباه تایپی در فرمولهای مقاله مرجع مربوط به این مثال است.
کلید واژه :,پروژه متلب,شبیه سازی با متلب,matlab project,پروژه های matlab,
Integro-differential equations, Numerical solution, Nonlinear, Haar wavelets, Collocation method
شبیه سازی
Haar wavelet method for nonlinear integro-differential equations
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.