توضیحات
FUZZY-SLIDING STATE-FEEDBACK CONTROL OF NONLINEAR BALL SUSPENSION SYSTEM
پروژه کنترل غیرخطی- خطی سازی فیدبک
در اینجا برخی از قسمت های گزارش حذف شده است.
مقدمه:
در این روش می خواهیم با اعمال یک u مناسب که از دو قسمت تشکیل شده است با استفاده از قسمت اول ، اثر غیر خطی بودن سیستم را دفع کنیم و با قسمت دوم پایداری و سرعت را تضمین کنیم.
این روش استفاده وسیعی هم در دنیای کنترل و هم در دنیای طبیعت دارد.
در مباحث کنترلی، برای پایداری می خواهیم با بدست آوردن یک قانون کنترل u حالت ها را از هر کجا در فضای به سمت صفر میل دهیم.
در مبحث ردیابی می خواهیم خروجی ، خروجی مطلوب را دنبال کند لذا باید قانون کنترل u را طوری بدست آوریم که از هر شرایط اولیه در فضای خطای ردیابی به سمت صفر میل کند و در ضمن تمام حالت ها محدود بمانند.
در این پروژه در بخش اول انواع روش های خطی سازی فیدبک توضیح داده می شود، در بخش دوم مدل سیستم مورد استفاده و شرایط لازم برای استفاده از خطی سازی فیدبک را مورد بررسی قرار خواهیم داد.
در بخش سوم نتایج شبیه سازی آورده می شود و در انتها نتیجه گیری بیان خواهد شد.
انواع روش های خطی سازی فیدبک
خطی سازی فیدبک به 2 صورت میباشد:
- روش خطی سازی ورودی- حالت
- روش خطی سازی ورودی- خروجی
در روش اول هدف آن است که با اعمال یک u مناسب ، حالتهای سیستم محدود شوند برای این منظور دنبال یک تبدیل غیر خطی هستیم که مختصات را تغییر دهد.
این تبدیل روی u اعمال می شود و کل سیستم را جابجا می کند.
ولی درروش دوم ما خروجی را پایدار و یا کنترل میکنیم و فقط دینامیک های داخلی سیستم را از نظر پایداری مورد بررسی قرار میدهیم.
روش خطی سازی ورودی – حالت
در روش خطی سازی ورودی – حالت سیستم های غیر خطی به فرم کلی زیر می باشند.
در واقع این روش از دو مرحله اساسی تشکیل شده است.
در مرحله اول با استفاده از تبدیلz=z(x) و یک قانون کنترلی غیر خطی مناسب به صورت u=u(x,v) اثر غیر خطی سیستم حذف می شود و مدل دینامیکی غیر خطی سیستم به یک مدل دینامیکی خطی به فرم تبدیل می شود.
سپس با اعمال یک قانون کنترل پایداری دینامیک خود سیستم یا دینامیک خطای سیستم تضمین می شود.
به طور معمول در مسئله خطی سازی ورودی – خروجی بحث پایداری داخلی و کنترل حالت های سیستم در شرایط اولیه خاصی مورد بررسی قرار می گیرد.
اما می توان از این روش برای مسئله ردیابی هم استفاده کرد.
البته معادله حرکت مطلوب باید بر اساس متغیر های جدیدی که برای تبدیل جبری لازم است به دست آید.
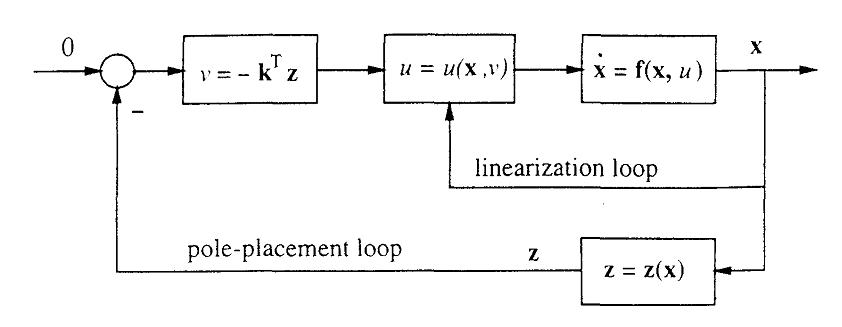
بلوک دیاگرام این روش کنترلی به صورت زیر می باشد.
همانطور که در بالا مشاهده می شود این سیستم کنترلی از دو حلقه داخلی و خارجی تشکیل شده است.
حلقه داخلی عمل خطی سازی دینامیک سیستم را بر عهده دارد و حلقه خارجی کار پایدارسازی سیستم غیر خطی را بر عهده دارد.
در این روش به طور معمول با توجه به نحوه انتخاب قانون کنترل غیر خطی برای خطی سازی دینامیک غیر خطی سیستم، قانون کنترل دارای نقطه یا نقاط تکینی می باشد که این مسئله حوزه پایداری سیستم را تحت الشعاع خود قرار می دهد.
از طرفی برای پیاده سازی این رویکرد کنترلی نیاز به اندازه گیری همه حالت ها می باشد زیرا به طور معمول حالت های جدید تعریف شده و قانون کنترلی غیر خطی به تمام حالت های سیستم وابسته می باشند.
نکته اساسی در مورد این روش این است که به طور کلی روش خطی سازی فیدبک به شدت وابسته به مدل سیستم است.
بنابراین برای پیاده سازی این روش از یک طرف باید سیستم را باید به خوبی شناخت.
از طرف دیگر اگر نامعینی در مدل یا پارامتر های سیستم رخ دهد این نامعینی یا عدم قطعیت روی عملکرد سیستم کنترلی تاثیر گذاشته و باعث تضعیف عملکرد آن می شود.
بنابراین این روش، یک روش کنترلی مقاوم نیست.
حال شرایط لازم برای استفاده از این روش را ذکر می کنیم.
فرض میکنیم معادلات سیستم به این صورت باشد:
- باید مجموعه زیر مستقل خطی باشد
- مجموعه زیر involutive باشد
اگر هر دو شرط برقرار بود میتوانیم z1 را از معادلات زیر به دست بیاوریم:
و در نهایت تبدیل حالت
و تبدیل ورودی به این صورت انجام میشود:
حال میتوان v را بگونه ای طراحی کرد که مسئله پایداری یا ردیابی را انجام دهد.
روش خطی سازی ورودی – خروجی
این روش کنترلی به طور معمول در مورد سیستم هایی به فرم زیر به کار می رود.
هدف کنترلی ما در اینجا به طور معمول ردیابی یک مسیر مطلوب می باشد.
ایده اساسی این روش این است که بتوان به طریقی ارتباط خطی و صریحی بین ورودی کنترل و خروجی تعریف شده برای سیستم پیدا کرد و سپس با اعمال یک قانون کنترل مناسب دینامیک سیستم را خطی کرد و سپس هدف ردیابی را برآورده کرد.
برای این منظور از خروجی تعریف شده برای سیستم تا زمانی که این ارتباط خطی و صریح بین ورودی و خروجی دیده شود مشتق گرفته می شود.
در نتیجه با توجه مرتبه مشتق خروجی درجه نسبی برای سیستم تعریف می شود.
از طرفی اگر درجه نسبی سیستم از مرتبه خود سیستم کمتر باشد.
بحث دینامیک داخلی پیش می آید.
در اینجا فقط اشاره می کنیم که اگر ما به هر طریقی توانستیم مدل دینامیکی خطی شده سیستم را پایدار کنیم هنوز کار تمام نشده است و باید پایداری دینامیک پنهان یا همان دینامیک داخلی سیستم را نیز بررسی کنیم.
زیرا این روش کنترلی در صورتی تضمین پایداری سیستم را می کند که دینامیک داخلی سیستم پایدار باشد.
برای بررسی پایداری دینامیک داخلی از مفهومی به نام پایداری صفر سیستم که یک ویژگی داخلی سیستم است استفاده می شود.
در این روش فرض بر این است که مشتقات خروجی تعریف شده و مسیر مطلوب معلوم بوده و کراندار می باشند.
همچنین قانون کنترلی مورد استفاده نیز ممکن است دارای نقطه یا نقاط تکین باشد.
در این روش نیز نیاز به اندازه گیری تمام حالت ها می باشد.
نکته مهم در اینجا این است که در این روش اگر درجه نسبی سیستم با مرتبه سیستم برابر باشد روش خطی سازی ورودی – خروجی به روش خطی سازی ورودی – حالت تبدیل می شود.
در روش خطی سازی ورودی – خروجی باید از خروجی تعریف شده برای سیستم مشتق بگیریم تا جایی که ارتباط خطی و صریحی بین ورودی و خروجی پیدا شود.
روند کلی این روش را می توان به مراحل زیر تقسیم کرد.
1) تعیین درجه نسبی سیستم از روی مرتبه مشتق خروجی
2) تعیین قانون کنترلی به طوری که معادله مشتق خروجی به صورت زیر در آید.
جایی که r درجه نسبی سیستم می باشد.
3) قانون کنترلی مناسب برای رسیدن به معادله بالا به صورت زیر می باشد.
4) تعیین v به صورتی که دینامیک خطای سیستم به سمت صفر همگرا شود.این قانون کنترل به صورت زیر می باشد.
برای تضمین پایداری دینامیک خطا ضرایب تا را باید به گونه ای به دست آورد که معادله تمام ریشه هایش سمت چپ محور موهومی باشد.
مدل سیستم مورد بررسی
می خواهیم یک توپ فلزی را با کنترل جریان مغناطیسی در مکان مطلوب قرار دهیم.
شکل مدل به صورت زیر می باشد.
معادلات حالت سیستم به صورت زیر می باشد.
که در آن می باشد.
C یک عدد مثبت است ما آن را 10 در نظر می گیریم.
ماتریس هایf و g را بدست می آوریم
همانطور که در بخش قبل گفته شد برای استفاده از روش خطی سازی فیدبک ورودی- حالت باید دو شرط استقلال خطی و involutive برقرار باشند.
بررسی شرط استقلال خطی:
برای بررسی استقلال خطی از mfile زیر استفاده شده است.
clear all
clc
syms x1 x2 x3
…
که rank(h) برابر 3 است پس شرط اول برقرار است.
بررسی شرط involutive :
با انتخاب شرط involutive هم برقرار می شود پس می توان از این روش خطی سازی استفاده کرد.
شبیه سازی:
سیستم اصلی بدون فیدبک خطی به صورت زیر می باشد.
…
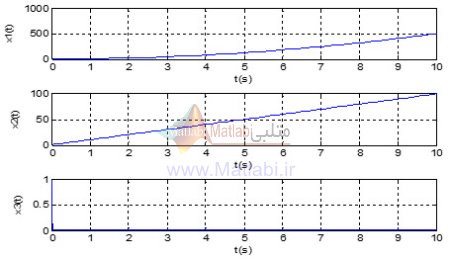
به ازای ورودی صفر و شرایط اولیه [1,1,1] حالت هایx1وx2 ناپایدار می باشد.
استفاده از خطی سازی فیدبک
سیستم شبیه سازی شده با در نظر گرفتن خطی سازی فیدبک به صورت زیر می باشد.
…
که زیر سیستم سیگنال کنترل به صورت زیر می باشد.
…
که درون Embedded Function به صورت زیر می باشد.
…
و v به صورت زیر می باشد.
function v = fcn(z1,z2,z3)
v=50*z1+60*z2+10*z3;
تغییر مختصات به صورت زیر می باشد.
function [z1,z2,z3] = fcn(x1,x2,x3)
…
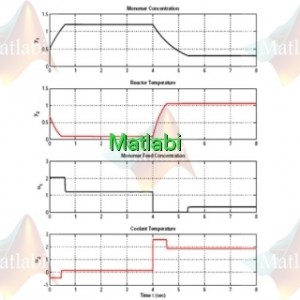
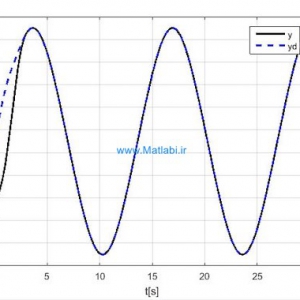
خروجی سیستم به ازای ورودی صفر و شرایط اولیه [-1,-1,-1] به صورت زیر می باشد.
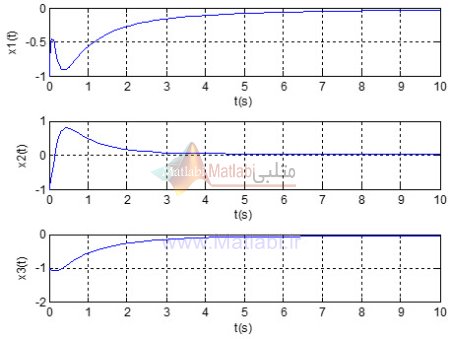
به ازای تغییر شرایط اولیه به [-2,2,-2] پاسخ سیستم و سیگنال کنترل به صورت زیر می باشد.
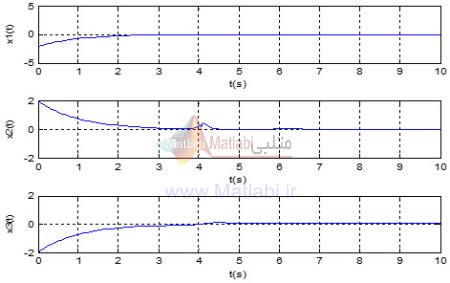
نتیجه گیری
روش خطی سازی فیدبک با تکنیک حذف اثر غیر خطی یک سیستم دینامیکی و استفاده از ابزار های کنترل خطی برای رسیدن به اهداف کنترلی یک روش طراحی کنترل کننده آسان و قابل فهم برای انواع زیادی از سیستم هاست.
آنچه که مشخص است این است که این روش قابلیت پایدارسازی داخلی یک سیستم و همچنین ردیابی یک مسیر مطلوب را به خوبی انجام می دهد.
اگر چه این روش محدودیت هایی دارد از آن جمله اینکه قانون کنترل به دست آمده به طور معمول دارای نقاط تکین می باشد و از طرفی در بعضی موارد خیلی بزرگ می باشد.
از طرفی این روش به شدت به مدل سیستم وابسته است و در برابر عدم قطعیت و اغتشاش مصون نیست.
کلید واژه : کنترل غیرخطی, خطی سازی فیدبک, پروژه متلب, پروژه matlab , شبیه سازی با متلب
fuzzy control, magnetic suspension, state-feedback control, sliding-mode control
شبیه سازی
FUZZY-SLIDING STATE-FEEDBACK CONTROL OF NONLINEAR BALL SUSPENSION SYSTEM
طبق توضیحات فوق به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.


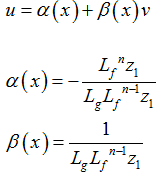

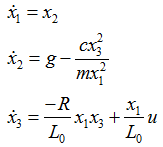
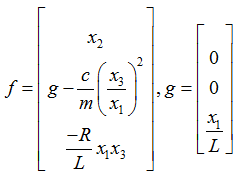





دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.