توضیحات
DESIGN OF STABILIZING SIGNALS BY USING MODEL PREDICTIVE CONTROL
شبیه سازی تثبیت کننده پایداری سیستم بر مبنای کنترل پیش بین (MPC)
مقدمه
کنترل پیش بین مدل (Model Predictive Control یا MPC) نوعی کنترل پیشرفته فرایند است که از دهه ۱۹۸۰ در صنایع فرایند، صنایع شیمیایی و پالایشگاههای نفت به کار میرود.
اخیراً از این کنترل کننده در مدلهای بالانس سیستمهای قدرت نیز استفاده شده است.
در این کنترل کنندهها از مدلهای دینامیکی فرایند، که عمدتاً از مدلهای تجربی، که با شناسایی سیستم به دست میآیند، استفاده میشود.
مهمترین مزیت MPC بهینهسازی تابع هزینه با درنظر گرفتن مقادیر آینده، میباشد.
این کار با بهینه سازی یک افق زمانی محدود اما اجرای آن تنها زمان نمونهبرداری جاری انجام میگیرد.
کنترل کننده MPC، توانایی پیش بینی رخدادهای آینده و اتخاذ اعمال کنترلی متناسب با آن را دارد.
مدلهای به کاررفته در MPC معمولا” مدلهایی برای نشان دادن رفتار یک سیستم دینامیکی پیچیده هستند.
الگوریتم کنترل پیش بین پیچیدگی سیستم را افزایش میدهد و برای کنترل سیستمهای ساده که اغلب با کنترل کنندههای PID به خوبی کنترل میشوند استفاده از این کنترل کننده توصیه نمیشود.
از مشخصههای دینامیکی رایجی که معمولاً برای کنترل کنندههای PID مشکل ایجاد میکنند، میتوان به تآخیرهای زمانی طولانی و دینامیکهای مرتبه بالا اشاره کرد.
تغییرات متغییرهای وابسته که نتیجه تغییرات متغییرهای نابسته هستند، با استفاده از مدلهای MPC پیش بینی میشوند.
در یک فرایند شیمیایی متغییرهای نابستهای که میتوان با کنترلر تغییر داد اغلب یا نقاط تنظیم (set point) کنترل کنندههای PID رگولاتوری (فشار، فلو، دما…) هستند یا عنصر کنترلی نهایی (ولو، دمپر…).
متغییرهای نابستهای که نمیتوان با کنترل کننده تنظیم کرد به عنوان اغتشاش به کار میروند.
متغییرهای وابسته در این فرایندها دیگر اندازه گیریهایی هستند که یا اهداف کنترلی را نشان میدهند یا محدودیتهای کنترلی.
کنترل کننده MPC با استفاده از اندازه گیریهای فعلی از سیستم تحت کنترل، حالت دینامیکی فعلی فرایند، مدلهای MPC و اهداف و محدودیتهای متغییر فرایند، تغییرات آتی متغییرهای وابسته را محاسبه میکند.
این تغییرات به گونهای محاسبه میشوند که متغییرهای وابسته نزدیک به هدف بمانند و محدودیتها روی متغییرهای نابسته و وابسته رعایت شود.
معمولاً MPC تنها اولین تغییر در هر متغییر نابسته را برای اجرا میفرستد و محاسبه را برای تغییر بعدی تکرار میکند.
با وجود آنکه بسیاری از فرایندهای واقعی خطی نیستند اغلب می توان آنها را در بازه کوچکی خطی در نظر گرفت.
روشهای MPC خطی در بیشتر کاربردها با مکانیسم فیدبک به کار می روند که خطاهای پیش بینی ناشی از عدم تطبیق بین مدل و فرایند را جبران می کند.
در کنترل کننده های پیش بین که تنها از مدلهای خطی تشکیل می شوند اصل برهم نهی (جمع آثار) جبر خطی امکان می دهد اثر تغییرات متغییرهای نابسته چندگانه برای پیش بینی پاسخ متغییر وابسته با هم جمع شوند.
با این کار مسئله کنترلی به یک سری محاسبات جبری ماتریسی مستقیم ساده می شود که سریع و مقاوم هستند.
هنگامي كه مدلهاي خطي به اندازه كافي براي نشان دادن غيرخطي بودن واقعي مدل دقيق نيستند از روشهاي گوناگوني مي توان استفاده كرد.
در برخي موارد مي توان از تغيير متغييرهاي فرايند پيش و/يا پس از مدل خطي براي كاهش غير خطي بودن استفاده كرد.
فرايند را مي توان با MPC غير خطي كه مستقيما” از مدل غير خطي استفاده مي كند كنترل كرد.
مدل غير خطي مي تواند به شكل يك برازش منحني تجربي (مانند شبكه هاي عصبي مصنوعي) يا يك مدل ديناميكي دقيق بر مبناي توازن بنيادي جرم و انرژي باشد.
مدل غير خطي را مي توا ن براي به دست آوردن فيلتر كالمن و يا استفاه از آن در MPC خطي، خطي سازي كرد.
چرا کنترل پیشبین؟
از دلایلی که برای استفاده از کنترل پیشبین میتوان به آن اشاره کرد، وجود تاخیر و کندی در سیستمها میباشد.
در سیستمهای تاخیر دار به دلیل این که اطلاعات خروجی سیستم دیر به دست کاربر میرسند، لذا به منظور اینکه از جهت گیریهای ناخواسته خروجی جلوگیری شود، لازم است آینده پیشبینی شود.
از طرفی به دلیل اینکه در کنترل پیشبین غیرخطی محاسبات زیادی انجام میشود، لذا باید زمان نمونهبرداری به حدی کافی باشد که پروسسور بتواند محاسبات لازم را انجام دهد.
لذا در سیستمهای کند همانند سیستمهای فرآیندی با زمان نمونهبرداری زیاد به دلیل فرصت کافی برای انجام محاسبات، استفاده از این کنترلکننده قابل قبول است.
ساختار کنترل پیشبین
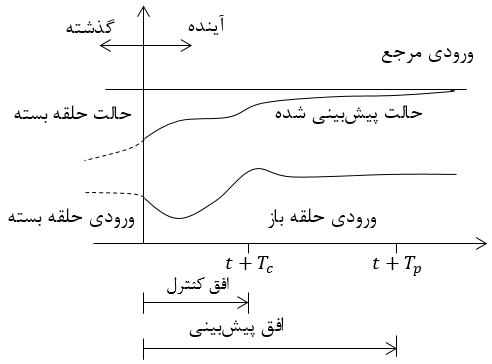
کنترل پیشبین را میتوان به نوعی یک مسئله بهینه سازی دانست که در هر گام یا زمان بهینه سازی حل میشود.
در واقع این مسئله تلفیقی از کنترل بهینه، مدلسازی و بهینهسازی ریاضی میباشد.
در شکل 1-1 اساس کارکرد این کنترل کننده نشان داده شده است، همانطور که در شکل نشان داده شده است مقادیر سیگنال کنترلی و خروجی سیستم در لحظهt و قبل از آن کاملا مشخص بوده و کنترل پیشبین بر اساس مدلی که از سیستم در اختیار دارد مقادیر خروجی آینده، در افق پیشبین Tpرا تخمین زده و با حل یک معادله بهینهسازی مقادیر سیگنال کنترل را در افق کنترلTu بدست میآورد.
بنابراین سیگنال کنترل بدست آمده، شرایط معادله بهینه سازی را ارضا کرده و به سیستم اعمال می-شود؛ در گام بعدی همین روند تکرار میشود.
توجه داریم که در شکل سیگنال کنترلی یک سیگنال اختیاری است.
اجرای روند الگوریتم
در کل، الگوریتمهای MPC روند مشترکی دارند، که به 3 مرحله تقسیم میشوند.
این مراحل به ترتیب اولویت به صورت زیر میباشند:
- مدل پیشبین
- تابع هزینه
- سیگنال کنترل
مدل پیشبین
اصلیترین بخش در کنترل پیشبین مبتنی بر مدل، مدلسازی سیستم و به دست آوردن یک مدل مناسب از سیستم میباشد.
در بسیاری از مقالات مدلهای متفاوتی برای کنترل پیشبین در نظر گرفته شده و نتایج بررسی شده است.
در کنترل پیشبین دو عامل بر کیفیت کنترل اثر میگذارد، این دو عامل مدل و پارامترهای کنترلی میباشند.
از آنجا که مدل اصلی ترین قسمت از تابع بهینه سازی را تشکیل میدهد، لذا رسیدن به مدلی مطلوب و با کیفیت در اولویت است.
تابع هزینه
در کنترل پیشبین هدف از بهینه سازی بدست آوردن سیگنال کنترلی است که با اعمال آن به سیستم، خروجی در یک افق معین از سیگنال مرجع مشخصی پیروی کند.
عبارت معمول برای تابع هزینه به صورت زیر در نظر گرفته میشود.
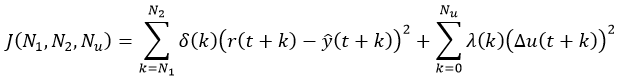 |
در این رابطه و افق پیشبین، و افق کنترل میباشد.
پارامترهایN1 و N2 پارامترهایی هستند که به نوعی جنبه احساسی دارند، در صورتی که افق پیشبین بزرگ در نظر گرفته شود چنانچه در لحظات اولیه خطا بزرگ باشد چندان اهمیت نخواهد داشت.
در صورتی که پروسه دارای تاخیری برابر dباشد، دلیلی برای کمتر گرفتن مقدار ابتدایی افق از d وجود ندارد زیرا در لحظه قبل از تاخیر، خروجی مقداری ندارد.
از طرفی چنانچه سیستم غیر مینیمم فاز باشد جمله اول اجازه لحاظ نشدن پاسخ معکوس در معادله بهینهسازی را صادر میکند.
بدست آوردن قانون کنترل
در نهایت، با حل معادله بهینهسازی ، مقدار سیگنال کنترل به صورت یک بردار بدست میآید که اولین عنصر این بردار سیگنال کنترلی است که باید به سیستم اعمال شود.
الگوریتمهای متداول کنترل پیشبین
تاکنون انواع الگوریتمهای متفاوتی برای کنترل پیشبین ارائه شدهاند، که در این کنترلکنندهها روند همانند قبل یعنی پیشبینی، بهینه سازی و سیگنال کنترلی میباشد.
این کنترلکننده ها به شرح زیر میباشند:
- کنترل کننده ماتریسی دینامیکی (DMC)
- کنترل خود تنظیم پیشبین گسترش یافته (EPSAC)
- کنترل پیشبین تعمیم یافته (GPC)
- کنترل الگوریتمیک مدل(MAC)
- کنترل تابعی پیشبین (PFC)
- کنترل ماتریسی دینامیکی کنترل (QADMC)
- بهینهسازی حلقه بازترتیبی (SOLP)
- و …
از میان مدلهای فوق کنترل پیشبین تعمیم یافته که از مدل تابع تبدیل سیستم استفاده میکند، از محبوبیت بیشتری در صنعت برخوردار است.
این الگوریتم توسط کلارک پیشنهاد شد و به یکی از محبوبترین روشهای کنترل پیشبین در صنعت تبدیل شد.
ایده اصلی در این کنترل کننده همان ایده کمینه کردن تابع معیار مورد نظر است که طی آن یک بردار سیگنال کنترل بدست آمده که از این بردار اولین عنصر به سیستم اعمال میشود.
در اواخر دهه 70 که DMC توسط کاتلر مطرح شد، به طور همزمان کنترل الگوریتمیک مدل معرفی و در شرکت آدرسا استفاده شد.
در این روش از مدل پاسخ ضربه استفاده میشود.
در این قسمت فقط به چند روش محبوب اشاره شد و در کل توضیح هر کدام از این کنترل کنندهها از حوزه این بحث خارج بوده و از آن میگذریم.
کنترل پیشبین غیرخطی
یکی از قدرتمندترین الگوریتمهای کنترلی که برای سیستم های غیرخطی ارائه شده کنترل پیشبین غیرخطی است که موضوع بسیار محبوبی برای تحقیق و پژوهش است.
در بسیاری از سیستمها، در نزدیکی حالت ماندگار با استفاده از خطیسازی، یک مدل خطی به سیستم نسبت داده میشود که با استفاده از این مدل میتوان یک کنترل کننده خطی با کارایی مناسب جهت کنترل سیستم پیشنهاد کرد.
اما در بعضی فرآیندها به دلیل درجه غیرخطیگری بالای سیستم، پایداری حلقه بسته تحت تاثیر قرار گرفته که در نهایت استفاده از مدل خطی به تنهایی پاسخگو نیست.
بنابراین در چنین فرآیندهایی، از مدل سازی غیرخطی حول نقطه کار مورد نظر استفاده میشود.
از طرفی با توجه به اینکه کنترل پیشبین غیرخطی از مدل غیرخطی سیستم به منظور تحقق اهداف کنترلی استفاده میکند، به کنترل کنندهای محبوب جهت کنترل سیستمهای غیرخطی تبدیل شده است.
کنترل پیشبین مدل شبکه عصبی
شبکههای عصبی به دلیل انعطافپذیری بالا برای کنترل سیستمهای غیرخطی استفاده میشوند.
از جمله کاربردهای مهم این ابزار میتوان به کنترل پیشبین غیرخطی اشاره کرد، جاییکه شبکه عصبی وظیفه تخمین خروجی سیستم را بر عهده دارد.
در سیستمهای کنترلی که وظیفه مدلسازی بر عهده شبکه عصبی است، تحت عنوان روش غیر مستقیم یاد میشود.
در این حالت هدف بهینه سازی یک تابع هزینه است.
کنترل کنندههای مستقیم در محدوده کنترل کنندههای مدل آزاد و کنترل کنندههای غیر مستقیم در محدوده کنترل کنندههای مبتنی بر مدل قرار میگیرند.
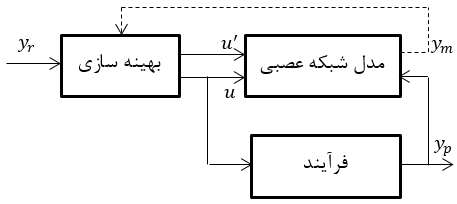
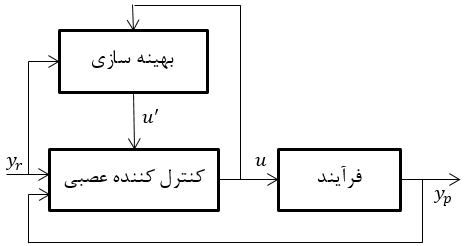
شکل های (1-2) و (1-3) تفاوت کاربرد شبکه عصبی به عنوان کنترل کننده مستقیم و غیر مستقیم را نشان میدهد.
شکل2- 2: شبکه عصبی به عنوان کنترل کننده غیر مستقیم
شکل2- 3: شبکه عصبی به عنوان کنترل کننده مستقیم
بهینه سازی تابع هزینه در کنترل پیشبین غیرخطی
در حالت کنترل پیشبین خطی، با برابر صفر قرار دادن گرادیان تابع هزینه میتوان سیگنال کنترلی را سر راست مشخص کرد.
ولی در حالت غیرخطی باید با استفاده از بهینهسازی عددی به حل مسئله پرداخت.
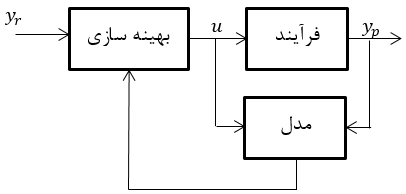
ابتدا بلوک دیاگرام کنترل پیشبین با حل مسئله بهینهسازی به صورت زیر است.
شکل2- 4: ساختار حل مسئله بهینهسازی در کنترل پیشبین غیرخطی
روش بهینهسازی غیرخطی به دو دسته مربعی و غیرمربعی تقسیم میشود.
در دسته مربعی تابع هزینه شکل مربعی دارد که به صورت زیر است.
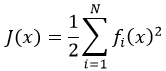 |
(2‑2) |
در بهینه سازی تابع هزینه مربعی راههای ساده تری از حالت کلی تدوین شده است که در ادامه به آنها پرداخته شده است.
بهینه سازی به دو صورت مقید و نامقید انجام میشود، در حالت مقید، نقطه بهینه علاوه بر مینیمم کردن تابع هزینه، باید یکسری قیود را برآورده کند.
در حالت نامقید قیودی وجود نداشته و تنها هدف یافتن نقطه کمینه کلی است. علاوه بر این، بهینه سازی غیرخطی خود به دو صورت یافتن مینیمم محلی و کلی تقسیم میشود. انجام پروژه متلب با سایت معتبر متلبی
روش بهینه سازی کلی، نقطه مینیمم کلی را در کل فضای کاری پیدا میکنند در صورتی که روش بهینهسازی محلی تنها در یک بازه کاری مسئله را حل کرده و نقطه بهینه را معرفی میکند.
در صورتی که تابع بهینهسازی تعریف شده در کل بازه کوژ باشد، کمینه محلی همان کمینه کلی است.
از جمله روشهای مشهور در بهینه سازی میتوان به الگوریتم ژنتیک، روشهای چند شروع، برنامه ریزی مربعی ترتیبی، گرادیان نزولی، روش نیوتن، گاوس نیوتن، شبه نیوتن گرادیان مختلط، و Levenberg-Marquardt اشاره کرد.
در ادامه از تشریح همه خودداری کرده و فقط روش لونبرگ مارکوات به دلیل استفاده در این پروژه مورد بررسی میگیرد.
روش بهینه سازی Levenberg-Marquadt
همان طور که گفته شد این روش یکی از روشهای بهینهسازی تابع هزینه مربعی تعریف شده در قسمت قبل میباشد.
این روش مشابه روش نیوتن عمل میکند، توضیح اینکه روش نیوتن برای حل مسئله بهینه سازی در توابع معیار کاربرد فراوانی دارد.
اما یک مشکل این روش برخورد با حالتی است که ماتریس هسیان نقص رتبه پیدا میکند.
در صورت برخورد با این حالت نقطه ناایستا به عنوان کمینه معرفی خواهد شد.
در این حالت ناحیه اطمینان باید کوچکتر انتخاب شود.
از طرفی روش بیشترین شیب عملا رابطه زیر را درنظر میگیرد:
| (2‑3) |
روش بهینه سازی لونبرگ-مارکوات تلفیقی از دو روش فوق است، در این حالت با تلفیق دو روش فوق یک حالت تطبیقی بزحسب ناحیه اطمینان تعریف میکنند.
وقتی فاصله تا نقطه بهینه زیاد است، دقت تقریب گاوس نیوتن کم بوده و باید از روش بیشترین شیب استفاده کرد.
از طرفی با نزدیک شدن به نقطه بهینه و بهتر شدن تقریب گاوس نیوتن، نقص رتبه به وجود نمیآید.
و میتوان در این حالت به روش نیوتن تغییر وضعیت داد.
روش لونبرگ-مارکوات این دو روش را با یک ضریب تطبیقی با هم جمع میکند که در نهایت جهت از رابطه زیر بدست میآید:
| (2‑4) |
که در آن گام بهینه سازی میباشد.
در صورتی که مقدار کوچک باشد معادله فوق به روش نیوتن تبدیل میشود و در حالت عکس چنانچه این مقدار بزرگ باشد روش فوق به بیشترین شیب تبدیل میشود.
برای سوئیچ کردن بین دو روش معیار اصلی شرط کوچک بودن تابع هزینه است.
همچنین چنانچه مقدار به ویژه بودن نزدیک شود
آنقدر افزایش پیدا میکند که عبارت داخل پرانتز ناویژه شود.
در واقع روش لونبرگ-مارکوات از مزیت سرعت روش نیوتن استفاده میکند.
همچنین این روش عیب عمده روش نیوتن را رفع کرده و در ابتدای کار که لزوماً تابع حالت کوژ ندارد و در ناحیه اطمینان قرار ندارد، آن را با جستجوی بیشترین شیب جایگزین کرده است.
بیشترین شیب نیازی به محاسبه معکوس ماتریس نداشته و این مشکل را حل میکند. اما در مقابل، دقت و سرعت همگرایی کمتری دارد.
نحوه اجرای الگوریتم کنترل پیشبین
در این بخش نحوه اجرای الگوریتم کنترل پیشبین با استفاده از الگورتم بهینهسازی L-M توضیح داده میشود.
در مسئله کنترل پیشبین تابع هدف به صورت زیر میباشد:
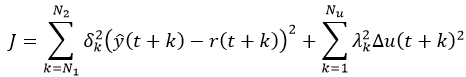 |
(2‑5) |
در این رابطه خروجی سیستم در لحظه
ورودی مرجع در لحظه
سیگنال کنترل اعمالی به سیستم در لحظه
وزنهایی هستند که اهمیت خطاها را مشخص میکنند.
به عنوان مثال یک انتخاب خوب برای این وزنها انتخاب یک تابع نمایی کاهش است که بیانگر این حقیقت است که خطاهای لحظات آینده نزدیک از اهمیت بالاتری نسبت به خطاهای آینده دور برخوردارند.
در این رابطه داریم:
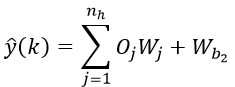 |
و
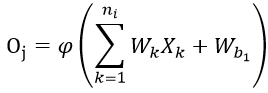 |
که در آن تابع عملکرد لایه میانی است.
همچنین ورودی سیستم و دینامیک ها میباشد.
و بقیه پارامترها وزنهای شبکه هستند که در حین آموزش مشخص میشوند.
به این ترتیب با استفاده از شبکه عصبی مقادیر خروجی در لحظات آینده تخمین زده شده و به تابع بهینه سازی داده میشوند.
حال در مرحله بعدی این تابع حل شده و در نهایت سیگنال کنترلی که باعث بهینه کردن این تابع معیار میشود، مشخص شده و به سیستم اعمال میشود.
این محاسبات برای یک زمان نمونهبرداری است و در حالت روی خط، پردازنده باید توانایی انجام محاسبات را در زمان یک نمونه برداری داشته باشد.
در زمانهای نمونهبرداری بعدی همین روند به طور متناوب اجرا میشود.
جمله دوم در معادله بهینه سازی، به دلیل جلوگیری از تغییر ناگهانی سیگنال کنترلی اضافه شده است.
در صورتی که این جمله وجود نداشته باشد، تغییرات شدید و نوسانی در سیگنال کنترل ایجاد شده که مطلوب نمیباشد.
از طرفی در حالت ماندگار تغییرات دامنه سیگنال کنترل یعنی جمله دون صفر بوده و در صورت استفاده از سیگنال کنترل خطای حالت ماندگار رخ خواهد داد.
جزئیات بیشتر در این باره در[1] آمده است.
در این پروژه هدف طراحی کنترل کننده GPC برای پایدار ساز سیستم های قدرت می باشد.
در ادامه الگوریتم کنترل پیش بین تعمیم یافته شرح داده می شود.
در این روش از ساختار CARIMA برای تحلیل استفاده می کنیم]2[.
این ساختار به شرح زیر است:
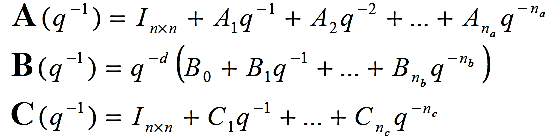
چند جمله ای های ، و صورت زیر است:
تابع هزینه GPC به صورت زیر می باشد:
که در آن به ترتیب ماکزیمم و مینیمم افق پیشبین می باشد و نیز افق کنترل.
نیز ضریب وزنی برای ورودی می باشد که برای راحتی در انجام محاسبات آنرا عددی ثابت در نظر می گیرند.
قسمتی از گزارش اینجا نیامده است و با خرید محصول قابل دسترس است.
پایدار ساز های سیستم های قدرت:
اکثر روشهای طراحی کنترل کننده ها با این فرض است که مدل نسبتاً دقیقی از سیستم در دسترس داشته باشند، این مدل ها عموماً پس از خطی کردن معادلات غیرخطی حول نقطه کار بدست می آید.
طراحی پایدارسازهای معمولی براساس بدترین نقطه کار جهت افزایش گشتاور میراکننده انجام می گیرد.
بدیهی است اگر تغییری در پارامترهای مدل رخ دهد نتایج استنتاج شده لزوماً صحت نخواهد داشت.
شاید کنترل تطبیقی یک انتخاب جهت تعقیب نقطه کار برای یک عملکرد رضایت بخش باشد، لکن انتخاب روش مناسب جهت شناسایی با توجه به تعداد پارامترها بصورت بلادرنگ و نرخ عملگرایی کند مشکلاتی دارد که عملاً از حد شبیه سازی تجاوز نکرده است.
یک روش عملی در طراحی پایدارسازهای سیستم قدرت اینست که باید عدم قطعیت ساختاری (تغییر پارامترها) و غیرساختاری (تغییر مدل سیستم) را در نظر بگیریم.
در این مقاله می خواهیم به کمک کنترل ترکیبی، غیرخطی فیدبک خطی ساز و ساختار متغییر هوشمند، پایدارسازی برای سیستم قدرت تک ماشینه مطابق طرح واره شکل 1 طراحی کنیم.
که با نصب آن روی هر نیروگاه بتواند پایداری گذرا و دینامیکی سیستم قدرت را در رنج وسیعی از عدم قطعیت ساختاری و غیرساختاری تضمین کند.
مدل سیستم در مرجع ]3[، به صورت زیر داده شده است:
این مدل، یک مدل خطی سازی شده است که از سیستم غیرخطی بدست می آید.
پارامترهای سیستم به صورت زیر داده می شوند:
که در آن
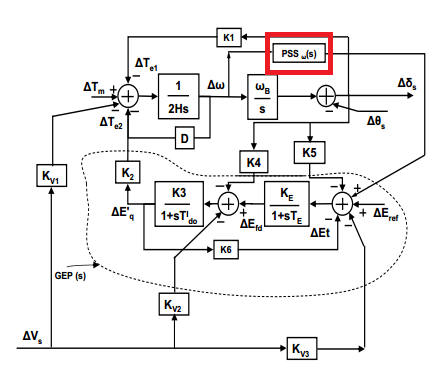
که در نهایت بلوک دیاگرام سیستم به صورت زیر می باشد:
شکل: بلوک دیاگرام سیستم و مکان قرار گرفتن کنترلر GPC
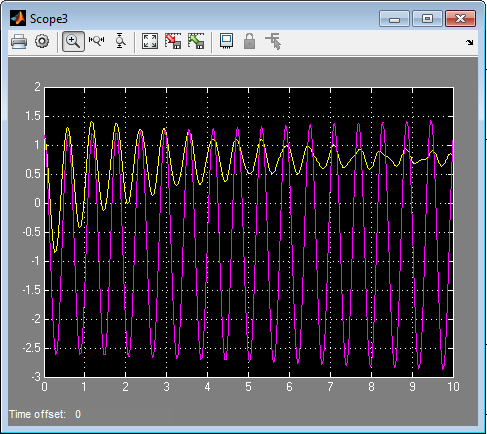
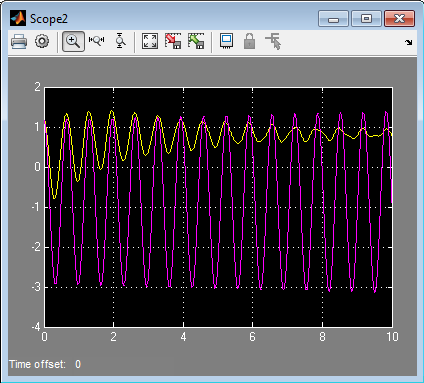
که در نهایت نتایج شبیه سازی با متلب به صورت زیر می باشند.
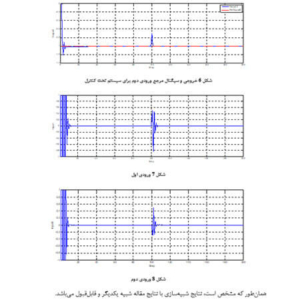
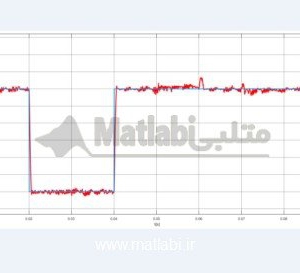
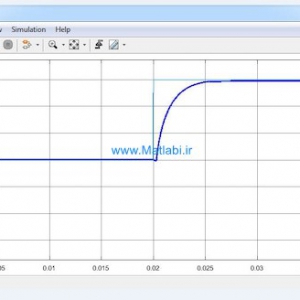
شکل 1: شبیه سازی مربوط به ماشین A
شبیه سازی مربوط به ماشین B
همانطور که مشاهده می شود، پایداری با استفاده از کنترل پیش بین به خوبی محقق می شود.
کلید واژه : , پروژه متلب, پروژه matlab , شبیه سازی با متلبpss
Model Predictive Control, Generalized Predictive Control, Low-Frequency Oscillations, PSS, SVC
شبیه سازی
DESIGN OF STABILIZING SIGNALS BY USING MODEL PREDICTIVE CONTROL
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.


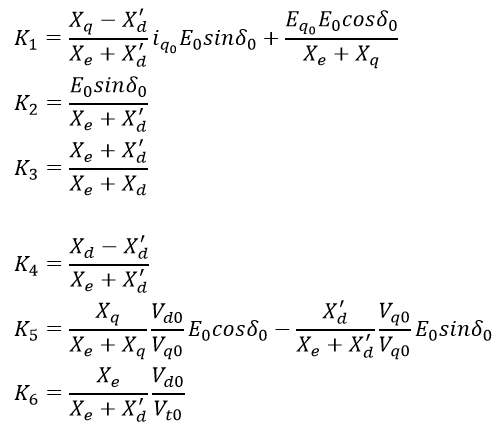
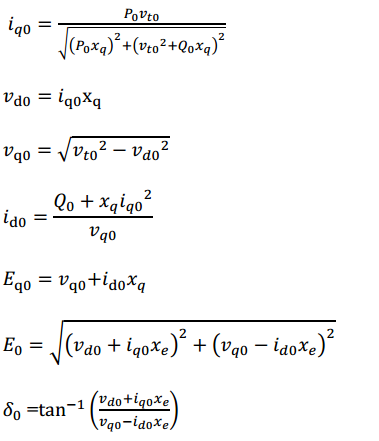



دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.