توضیحات
Design of Linear Quadratic Optimal Controller for Bicycle Robot
طراحی کنترل بهینه خطی درجه دوم برای ربات دوچرخه
بخشی از ترجمه مقاله:
چکیده
مدل دینامیکی ربات دوچرخه شبیه به مدل خطی می باشد وقتی در سرعت بالا در حرکت می باشد.با هدف حفظ تعادل دوچرخه در سرعت های بالا، گونه ای مدل دینامیکی خطی بر اساس مدل دینامیکی غیر خطی ربات دوچرخه ارائه شد.
حلقه ی باز پایداری براساس مدل دینامیکی خطی تجزیه و تحلیل شد و قابلیت کنترل پذیری و رویت و مشاهده ی از مدل پویا (دینامیکی) تایید شد. سپس محدوده ی مدل زمان از ربات دوچرخه بر اساس مدل خطی زمان پیوسته ارائه شد.
پس یک کنترلر بهینه ی خطی درجه دو (چهارگانه) براساس تئوری کنترل خطی برای مدل خطی دینامیکی ربات دوچرخه طراحی شد.
نتایج شبیه سازی کامپیوتر کارایی الگوریتم کنترلی را نشان می دهد. این برای آزمایش ربات دوچرخه ی واقعی در آینده امکان پذیر و عملی می باشد.
توضیحات برنامه
فایل زیپ شده ای که در اختیار شما قرار میگیرد حاوی دو پوشه با نام های Optimal Control for linear Dynamic و Optimal Control for Nonlinear Dynamic میباشد.
پوشه ی اول مربوط به دینامیک خطی و فضای حالت خطی گسسته ای است که در مقاله بدست آمده است، میباشد.
در این پوشه دو نوع ورودی متفاوت به سیستم اعمال شده است.یکی ورودی پله و دیگری یک نویز با توجه به شکل اخر مقاله به سیستم اعمال شده است. روند طراحی کنترلر بصورت زیر است:
خطوط اول تا سوم به ترتیب مربوط به پاک کردن صفحه ی اصلی متلب (command window)، پاک کردن داده ها (workspace) و در نهایت بستن تمامی نمودار هایی که قبل از این پروژه اجرا شده اند.
قسمت اول برنامه Data:
در این قسمت داده های موجود در مقاله در برنامه وارد میشوند.
قسمت دوم create System
در این قسمت فضای حالت سیستم پیوسته در محیط متلب تشکیل شده و بعد از آن مقادیر ویژه و بردارهای ویژه محاسبه شده اند.
قسمت سوم Calcute Co & Ob matrix
در این قسمت ماتریس های کنترل پذیری و رویت پذیری و رتبه ی آنها محاسبه شده و در نهایت کنترل پذیری و رویت پذیری سیستم با توجه به رتبه ی آنها بررسی میشود که این سیستم هم کنترل پذیر و هم رویت پذیر است.
قسمت چهارم simulation
این قسمت به کمک دستور sim به محیط سیمولینک مرتبط میشود.
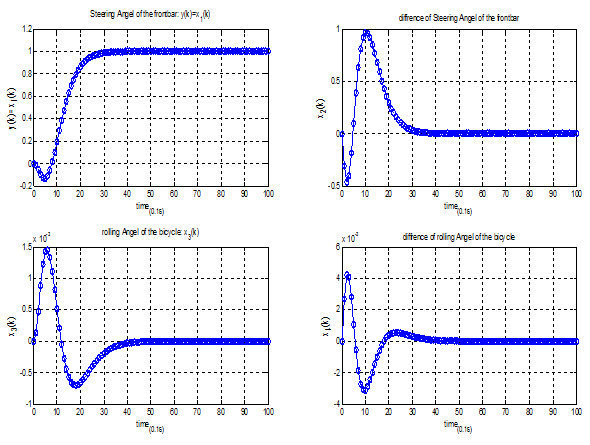
بعد از فراخوانی و اجرای فایل سیمولینک مقادیر حالت، زمان شبیه سازی و u را در نتایج رسم میکنیم.
نتایج به صورت زیر هستند.
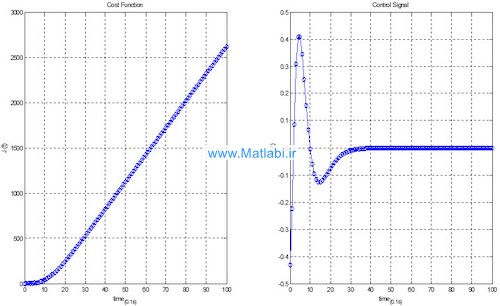
قسمت پنجم Plot Cost Function & Control Signal
در این قسمت با توجه به تابع هزینه ی تعریف شده در مقاله تابع هزینه را رسم میکنیم و همراه با سیگنال کنترلی بدست آمده از فایل سیمولینک در شکل زیر نشان میدهیم.
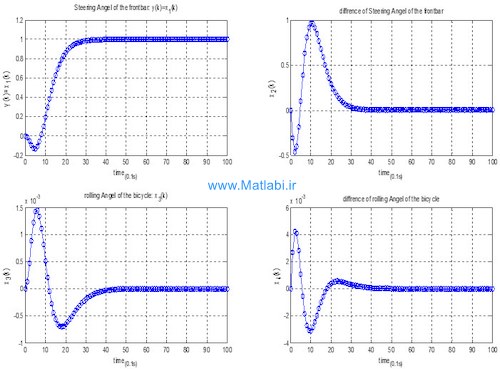
*** مراحل ذکر شده برای ورودی نویز هم به همین ترتیب بوده و نتایج آن به صورت زیر است.
*** اما در پوشه ی دوم با نام Optimal Control for Nonlinear Dynamic کنترلر طراحی شده برای سیستم غیرخطی را به دینامیک غیرخطی سیستم اعمال میکنیم. بلوک دیاگرام این سیستم در محیط سیمولینک به صورت زیر است.
…
در این شبیه سازی با کلیک کردن بر روی بلوک Nonlinear Dynamic برنامه ی زیر باز میشود که دینامیک غیرخطی روبات مدل شده است.
***اما نکته ی مهم مربوط به خط 21 میباشد.
چون کنترلری که طراحی شده است برای فضای حالت خطی گسسته تعریف شده است باید دینامیک غیرخطی را نیز ابتدا گسسته و سپس به آن کنترلر را اعمال کنیم.
که از روش اویلر استفاده شده است.
شرح روش اویلر برای تبدیل معادلات پیوسته به گسسته
…
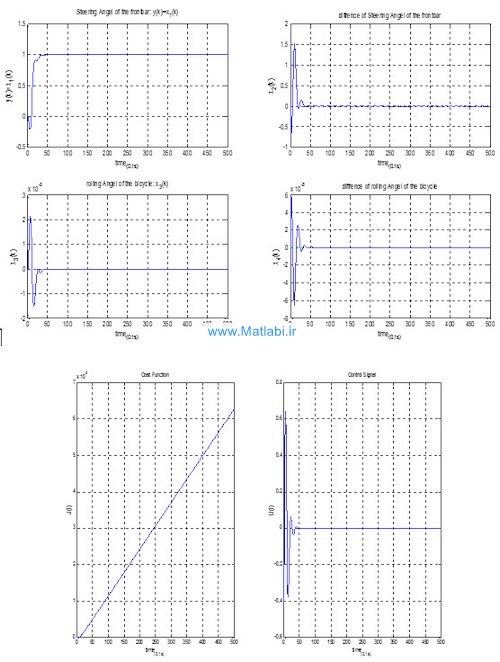
نتایج حاصل از اعمال کنترلر طراحی شده در قسمت قبل به سیستم غیر خطی به صورت زیر است:
کلید واژه : کنترل غیرخطی,
bicycle robot, Linear dynamic model, district , time model, linear quadratic optimal control, computer simulation
شبیه سازی
Design of Linear Quadratic Optimal Controller for Bicycle Robot
طبق توضیحات فوق به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.