توضیحات
DC Motor Position Control using State Space Technique
در زیر قسمتهایی از گزارش این شبیه سازی آمده است:
پروژه کنترل مدرن:
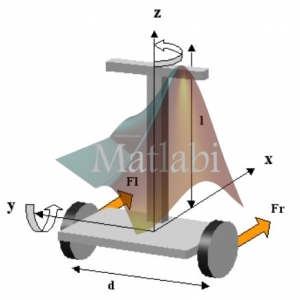
- سیستم انتخاب شده مدل یک سیستم موتور DC به صورت زیر می باشد.
…
می باشد که در آن مقادیر پارامترها به صورت زیر می باشد.
…
- برای به دست آوردن مقادیر و بردارهای ویژه از دستور eig استفاده می کنیم.
[h1,h2]=eig(A)
که در آن h1 بردارهای ویژه و h2 مقادیر ویژه سیستم داخل یک ماتریس قطری ارائه می شود .
h1 =
1.0000 -0.0147 – 0.0106i -0.0147 + 0.0106i
0 0.7835 0.7835
0 -0.5026 + 0.3651i -0.5026 – 0.3651i
h2 =
0 0 0
0 -35.0114 +25.4151i 0
0 0 -35.0114 -25.4151i
که در واقع مقادیر ویژه سیستم عناصر روی قطر اصلی ماتریس h2 می باشند.
ans =
0
-35.0114 +25.4151i
-35.0114 -25.4151i
این سیستم دو قطب مزدوج مختلط در سمت چپ محور jw دارد و یک قطب آن بر روی محور jw قرار گرفته است.
پاسخ پله سیستم به صورت زیر می باشد.
که بیانگر ناپایداری سیستم به ازای ورودی پله واحد می باشد.
- برای چک کردن کنترل پذیری از تابع … و برای چک کردن رویت پذیری از دستور … استفاده می کنیم در صورتی که رنک ماتریس های تشکیل شده کامل باشد نشان می دهد که ماتریس کنترل پذیر و یا رویت پذیر می باشد.
…
چون رنک هر دو ماتریس کامل می باشد پس بنابر این سیستم هم رویت پذیر و هم کنترل پذیر می باشد.
- پاسخ سیسستم به ازای ورودی پله واحد و شرایط اولیه دلخواه
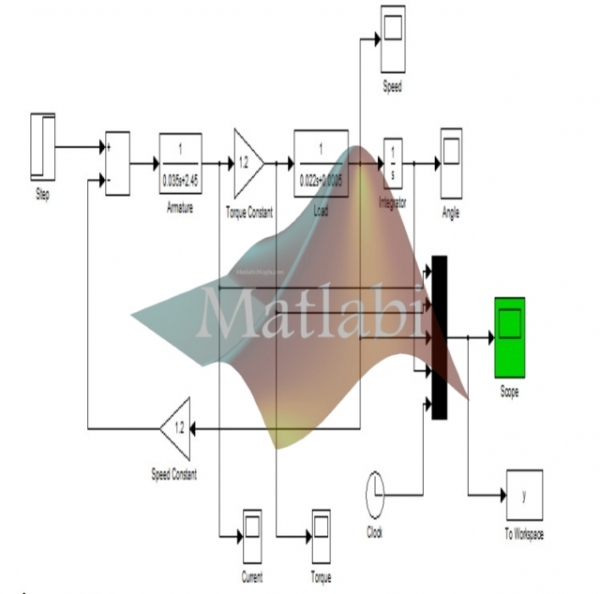
برای این کار ابتدا مدل فضای حالت سیستم را در محیط Simulink می کشیم.
شرایط اولیه را در داخل انتگرالگیر تعریف می کنیم.
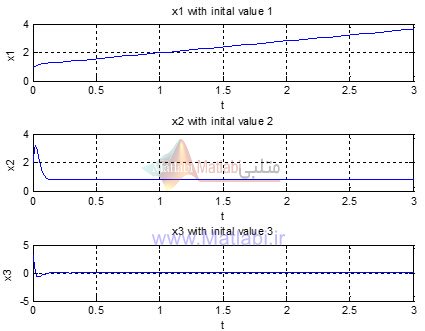
به ازای شرایط اولیه
x0=[1;2;3];
نتایج به صورت زیر می باشد.
به ازای شرایط اولیه
x0=[.1;-2;.003];
نمودار حالت ها به صورت زیر می باشد.
- طراحی حالت رگولاتوری:
با توجه به این که سیستم کنترل پذیر می باشد بنابر این می توان قطب های مطلوب سیستم را در هر جای دلخواهی قرار داد. می خواهیم کنترل کننده فیدبک حالتی طراحی کنیم که قطب های سیستم را در نقطه dis=[-3 ;-1+i ;-1-i];
برای به دست آوردن ماتریس K از دستور … استفاده می کنیم که خروجی این دستور ماتریسی است که گین فیدبک حالت را به ما می دهد.
dis=[-3 ;-1+i ;-1-i];
…
با اجرای این دستور گین فیدبک حالت برابر است با
gain =
0.0039 -1.1949 -2.2758
مدل فضای حالت سیستم را با وجود کنترل کننده فیدبک حالت در Simulink مدل می کنیم.
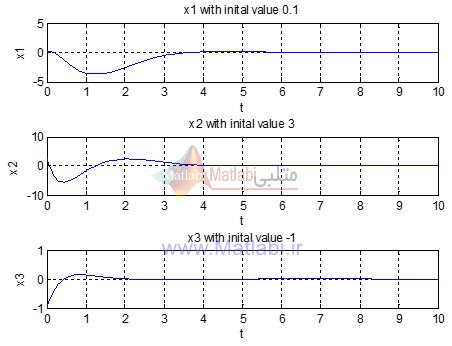
به ازای شرایط اولیه
x0=[.1;3;-1];
سیگنال کنترل و نمودار حالت ها برابر است با
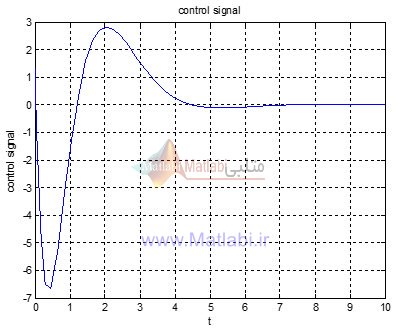
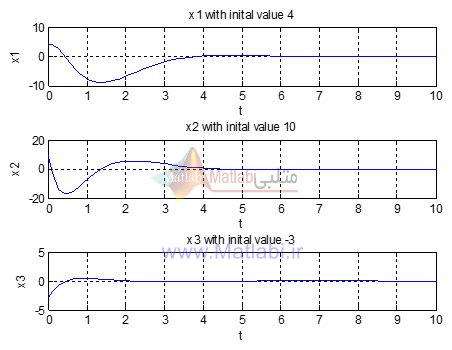
به ازای شرایط اولیه
x0=[4;10;-3];
نتایج برابر است با

برای حالت دوم می خواهیم قطب های مطلوب سیستم را از محور jw دور کنیم و سرعت سیستم را بهبود ببخشیم.
فرض می کنیم قطب های مطلوب در نقاط زیر قرار بگیرند.
dis=[-3 ;-2+2*i ;-2-2*i];
در این صورت گین فیدبک حالت برابر است با
gain =
0.0154 -1.1873 -2.2058
به ازای مقادیر اولیه
x0=[1;-1;-4];
نمودار سیگنال کنترل و حالت ها برابر است با
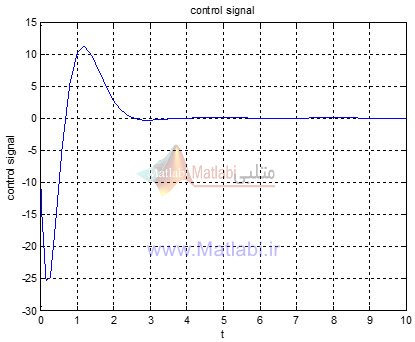
و به ازای حالت اولیه
x0=[.01;20;0];
نتایج برابر است با

همانطور که دیده می شود با دور کردن قطب های مطلوب سیستم از محور jw سرعت همگرایی حالت ها به سمت صفر افزایش پیدا کرده است.
6-طراحی حالت رگولاتوری yd ثابت
در این حالت نیز طراحی به صورت بند قبل می باشد با این تفاوت که ورودی مرجع پله واحد می باشد.
می خواهیم قطب های مطلوب سیستم در نقاط زیر قرار بگیرد.
dis=[-3 ;-1.5+sqrt(2)*i ;-1.5-sqrt(2)*i];
گین برابر است با
gain =
0.0082 -1.1916 -2.2408
نمودار سیگنال کنترل، حالت ها و خروجی به ازای شرایط اولیه زیر برابر است با
x0=[0;-2;-1];


کلید واژه : پروژه کنترل مدرن , پروژه متلب, پروژه matlab , شبیه سازی با متلب
Ackerman’s formula, DC motor, Graphical user interface, Integral control, State feedback controller
شبیه سازی
مدل سیستم مقاله DC Motor Position Control using State Space Technique
برای پروژه کنترل مدرن
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.











دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.