توضیحات
CLUSTER HEAD ELECTION USING IMPERIALIST COMPETITIVE ALGORITHM FOR WIRELESS COMPETITIVE ALGORITHM (CHEI)FOR WIRELES
به طور کلی سه الگوریتم 1-رقابت امپریالیست 2-LEACH 3-ژنتیک پیادهسازی شدهاند. فایل اصلی که برنامه اصلی در آن قرار دارد و با اجرای آن برنامه برای هر سه الگوریتم اجرا شده و نتایج را مشخص میکند فایل Main.m است. قبل از توضیح برنامه اصلی، کدهای نوشته شده برای هر سه الگوریتم را توضیح خواهیم داد.
کدهای Imperialist competitive algorithm
کدهای این برنامه در چند فایل و توابع مختلف نوشته شده است. هر فایل به طور جداگانه شرح و توضیح داده خواهد شد. بدنه اصلی الگوریتم ICA درون فایلی به همین نام قرار دارد. در ادامه به توضیح کدهای موجود در این فایل خواهیم پرداخت. لازم به ذکر است که برنامه ICA به تعداد مراکز خوشهها متغیر خواهد داشت و هر متغیر یک عدد که شماره راس کاندید برای مرکز خوشه بودن را مشخص میکند. هدف یافتن بهترین ترکیب از مراکز خوشهها به منظور بهینه کردن تابع هدف یا همان عبارت 22 مقاله است.
تابع هدف به منظور ارزیابی هر پاسخ تعریف شده است. اسم این تابع را تابع costfunction گذاشته و در ابتدا به ICA معرفی میکنیم تا معیاری برای ارزیابی خوشه بندی باشد.
%% Problem Statement
ProblemParams.CostFuncName = ‘CostFunction’; % You should state the name of your cost function here.
تعریف پارامتر اضافه برای تابع ارزیابی(در مدل طراحی شده پارامتر اضافی نداریم)
ProblemParams.CostFuncExtraParams = [];
تعیین تعداد متغیرهای برنامه که برابر با تعداد خوشه هاست
ProblemParams.NPar = cluster_number; % Number of optimization variables of your objective function. “NPar” is the dimention of the optimization problem.
بازه تغییرات هر عضو از جمعیت(کشور) ICA که بین 1 و تعداد رئوس است.
ProblemParams.VarMin = 1; % Lower limit of the optimization parameters. You can state the limit in two ways. 1) 2)
ProblemParams.VarMax = node_number; % Lower limit of the optimization parameters. You can state the limit in two ways. 1) 2)
تولید حد پایین و بالای هر متغیر به نسبت تعداد متغیرها و بازهای که قبلا مشخص شد
% Modifying the size of VarMin and VarMax to have a general form
if numel(ProblemParams.VarMin)==1
ProblemParams.VarMin=repmat(ProblemParams.VarMin,1,ProblemParams.NPar);
ProblemParams.VarMax=repmat(ProblemParams.VarMax,1,ProblemParams.NPar);
end
بازه از اختلاف حد بالا با پایین به دست خواهد آمد.
…
روش سوم که پیادهسازی شد روش الگوریتم ژنتیک بود. مقاله روشی ارائه داده بود و مرجع زده بود که متاسفانه در اینترنت قابل دسترسی نبود و گویا چنین مقالهای در google.scholar ثبت نشده بود. به همین دلیل یک مقاله مشابه با مقاله فعلی مربوط به سالهای اخیر پیدا شد که در ضمیمه نیز قرار دادم که از نظر عملکرد نیز خوب است و مقایسهای خوبی بین روش مقاله و روش ژنتیک خواهد بود. الگوریتم ژنتیک شامل دو فایل GA و GACostFunction است که به ترتیب هر دوی آنها توضیح داده خواهد شد. کلید روش پیشنهادی در طراحی تابع هدف یا همان GACostFunction است.
%Genetic algorithm
pop_number = 200;جمعیت الگوریتم ژنتیک برابر با کشورهای الگوریتم امپریالیست 200 در نظر گرفته شده است
max_itr = 100; حداکثر تکرار نیز مانند الگوریتم رقابت امپریالیستی 100 در نظر گرفته شده است
%population initiation
تولید جمعیت اولیه به صورت تصادفی
pops = randi([1 node_number],pop_number,cluster_number);
مقداردهی اولیه بهترین پاسخ و عناصر آن
BestSolVal = Inf;
BestSol = [];
شروع حلقه اصلی الگوریتم ژنتیک
%main loop
for ii=1:max_itr
فاز تقطیع و تولید دو فرزند از یک جفت والدین به تعداد 0.8*تعداد جمعیت
%cross_over phase
co = 1; %counter
for i=1:round(pop_number*.8)/2
pc = randperm(pop_number,2);%choose two different parents
new_pop(co,1:round(cluster_number/2)) = pops(pc(1),1:round(cluster_number/2)); %first part-first child
new_pop(co,round(cluster_number/2)+1:cluster_number) = pops(pc(2),round(cluster_number/2)+1:end); %second part-first child
new_pop(co+1,1:round(cluster_number/2)) = pops(pc(2),1:round(cluster_number/2)); %first part-first child
new_pop(co+1,round(cluster_number/2)+1:cluster_number) = pops(pc(1),round(cluster_number/2)+1:end); %second part-first child
…
الگوریتم LEACH
% %%%%%%%%%%%%%%%%%%%%%%%%LEACH phase
%cluster initiation using k-means
% [IDX,CE] = kmeans(node_location,cluster_number); %find centers
الگوریتم LEACH براساس انتخاب رئوسی که قبلا انتخاب نشدهاند رفتار میکند، به همین دلیل یک ماتریس به نام selected برای تعیین انتخاب شدن یا نشدن مقدار دهی اولیه میکنیم
selected = zeros(node_number,1);
% %find cluster head nodes
% for i=1:size(CE,1)
% D = sqrt(sum((node_location – repmat(CE(i,:),node_number,1)).^2,2));%one to other nodes distance
% [~,ind] = min(D);
% centers(i) = ind;
% selected(centers(i)) = node_number/cluster_number;
% end
%
% cluster_location = node_location(centers,:);
% BestSol = centers;
% %assign nodes to clusters
% for j=1:size(node_location,1)
% D = sqrt(sum((cluster_location – repmat(node_location(j,:),length(centers),1)).^2,2));%fasele marakez ta sink
% [~,ind] = min(D);
% %clusters(j) = centers(ind);
% clusters(j) = (ind);
% end
%continues phase
…
الگوریتم ژنتیک – کدهای این بخش نیز دقیقا مانند بخش قبل است و فقط دستور GA به جای LEACH استفاده شده است. تصاویر در پوشه GA pic ذخیره خواهند شد….
پس از پایان برنامه سه نمودار برای انرژی باقی مانده در هر مرحله، رئوس باقی مانده و هزینه ارسال و دریافت بستهها رسم خواهد شد.
%plot residual energy
figure; plot(res_energy(:,1),’-o’); hold on; plot(res_energy(:,2),’r-+’); hold on; plot(res_energy(:,3),’k-s’);
legend(‘ICA’,’LEACH’,’GA’); title(‘Residual Energy’);
%plot alive nodes
figure; plot(alive_nodes(:,1),’-o’); hold on; plot(alive_nodes(:,2),’r-+’); hold on; plot(alive_nodes(:,3),’k-s’);
legend(‘ICA’,’LEACH’,’GA’); title(‘Number of alive nodes’);
%plot costs
figure; plot(Costs(:,1),’-o’); hold on; plot(Costs(:,2),’r-+’); hold on; plot(Costs(:,3),’k-s’);
- legend(‘ICA’,’LEACH’,’GA’); title(‘Costs’);
- تعهدات واحد محرمانه ی امنیت (SCUC) و آن حل با الگوریتم رقابتی اصلاح شده امپریالیست (MICA)
چند نمونه از نمودارهای برنامه
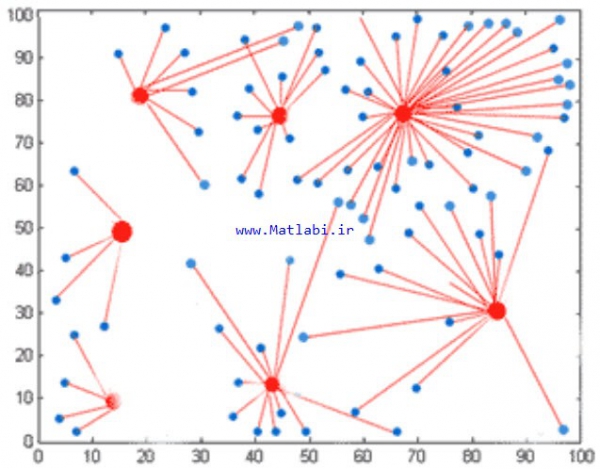
با اجرای برنامه، ابتدا الگوریتم ICA که به دلیل محاسبه سنگین تابع ارزیابی کند پیش میرود، شروع شده و نتایج آن مرحله به مرحله مانند تصویر زیر نمایش داده خواهند شد.
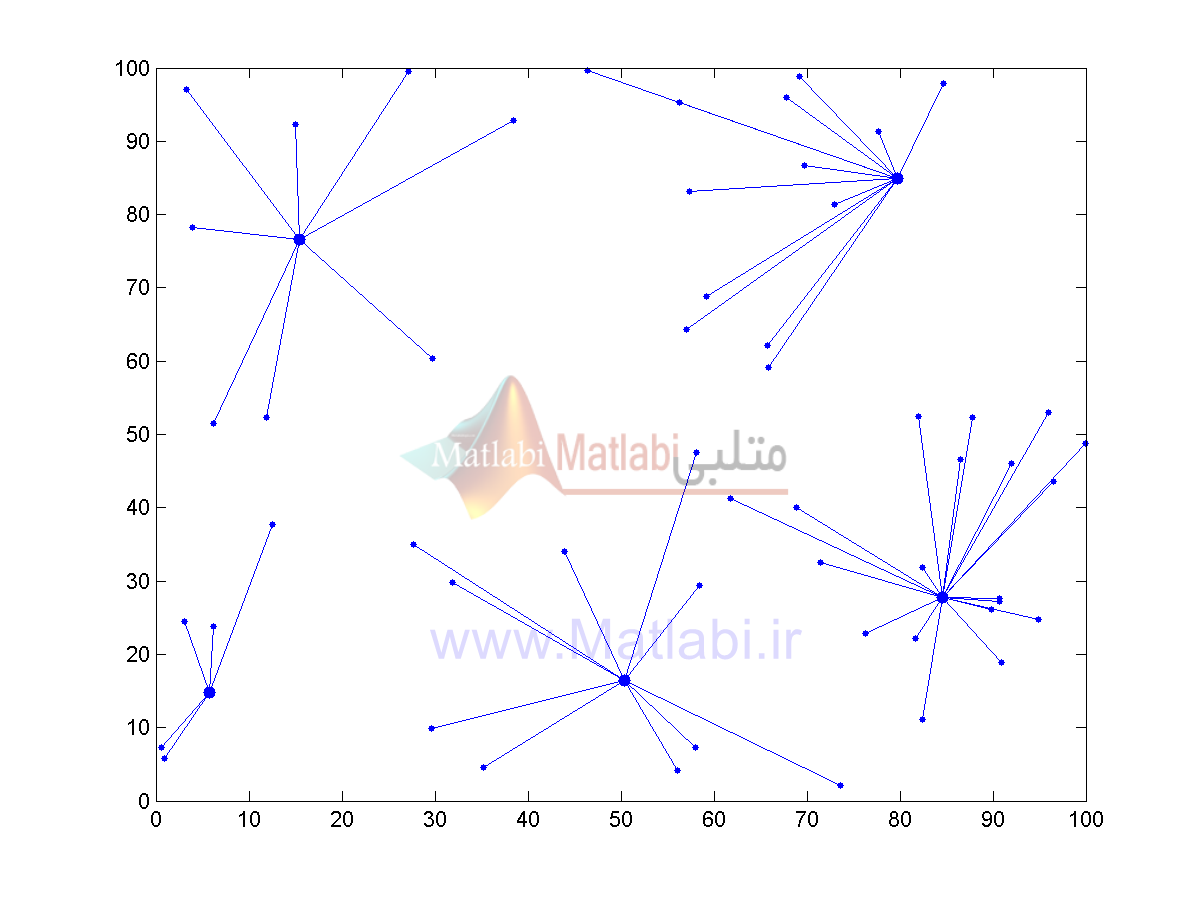
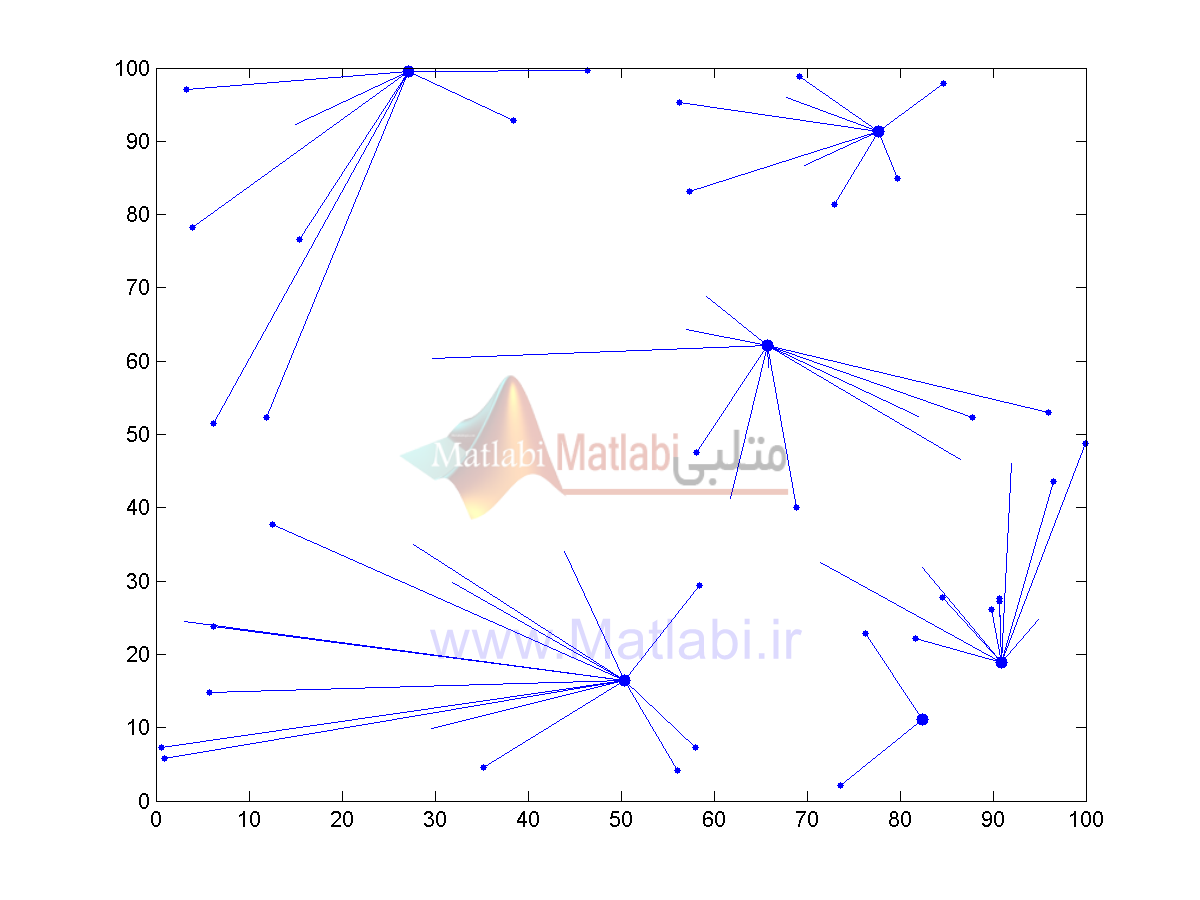
تصویر بالا مرحله17(تکرار 17) الگوریتم ICA را نشان میدهد. تمام مراحل شبیهسازی که یک بار اجرا شدهاند همانطور که پیشتر گفته شد در پوشه ICA pic قابل دسترسی و مشاهده است. همین مرحله در الگوریتم LEACH به شکل زیر است.
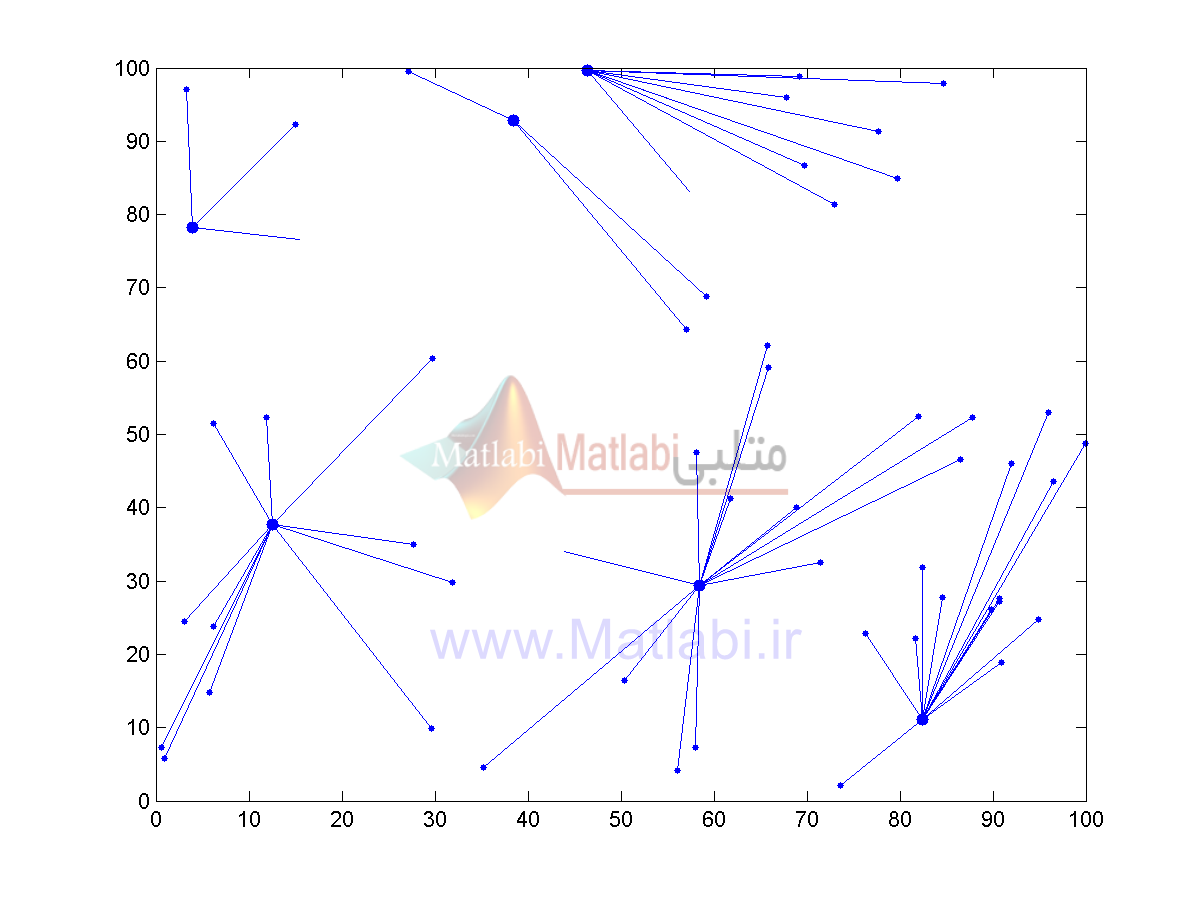
همانطور که مشخص است، الگوریتم ICA به جای 6 خوشه به تشخیص خودش از 5 خوشه استفاده کرده زیرا همانطور که مشخص است میتوان به جای دو خوشه سمت راست-پایین از یک خوشه استفاده کرد و این یک ویژگی روش پیشنهادی مقاله است. شکل زیر مرحله17 الگوریتم ژنتیک را نشان میدهد. این الگوریتم مانند الگوریتم LEACH خوشههای نزدیک به هم تولید کرده که باعث افزایش هزینه و انرژی خواهد شد.
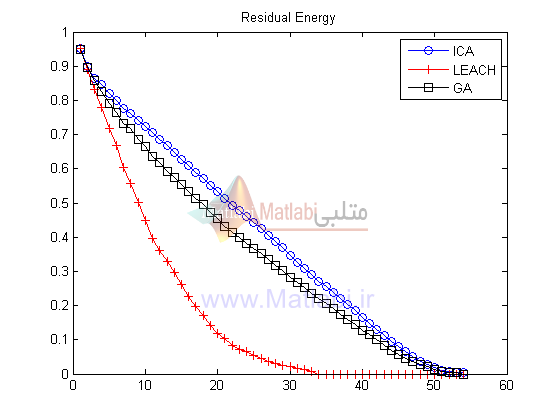
همانطور که گفته شد سه الگوریتم نیز در پایان برنامه نمایش داده خواهند شد. تصویر زیر مقایسه هر سه روش در انرژی باقیمانده رئوس در هر مرحله است. روش پیشنهادی به شکل محسوسی از روش LEACH بهتر و با کمی اختلاف از ژنتیک بهتر است.
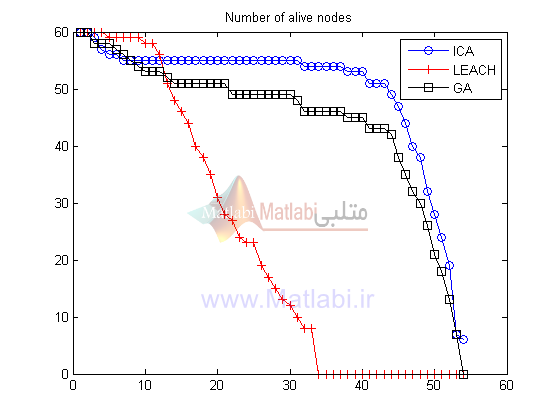
نمودار زیر نیز تعداد رئوس زنده در هر مرحله را نشان میدهد.در این بخش نیز رفتار الگوریتم ICA از دو روش دیگر بهتر است.
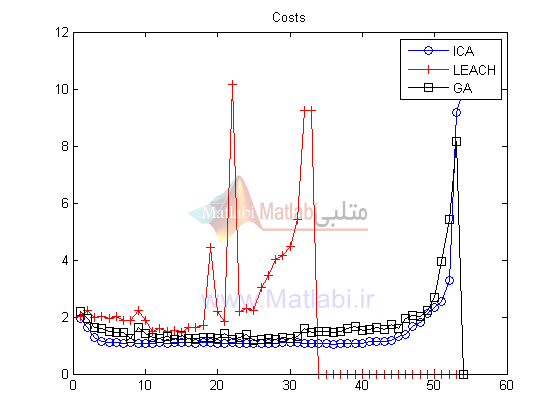
در نهایت تابع هزینه معرفی شده در عبارت22 به عنوان مقایسه هزینهها در نظر گرفته شده است که در تصویر زیر میتوانید نتیجه آن را نیز مشاهده کنید. الگوریتم LEACH تا تکرار 30 هزینه بیشتری را به دست آورده و ICA دقیقا عکس آن عمل کرده است. دلیل 0 شدن هزینه LEACH از تکرار 30 به بعد، پایان یافتن عمر رئوس با پایان یافتن هزینه آنهاست که ضعف این مدل در مقابل روش مقاله است.
کلید واژه : شبکه های بیسیم، کلاستر، مصرف انرژی, پروژه متلب,شبیه سازی بامتلب
Wireless Sensor Networks, Clustering, Imperialist competitive algorithm, ICA, Energy Consumption, Cluster Head Election
شبیه سازی مقاله CLUSTER HEAD ELECTION USING IMPERIALIST COMPETITIVE ALGORITHM FOR WIRELESS COMPETITIVE ALGORITHM (CHEI)FOR WIRELES
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.




دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.