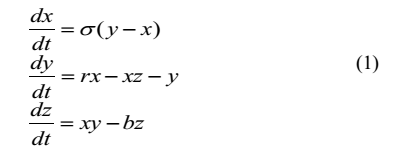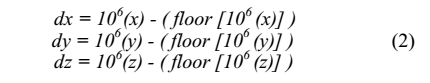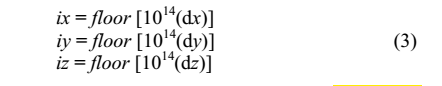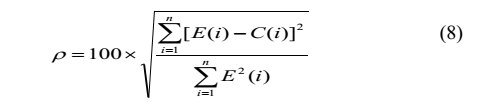توضیحات
Chaos-based Encryption of Biomedical EEG Signals using Random Quantization Technique
رمزنگاری برمبنای آشوب سیگنال های EEG با استفاده از تکنیک تعیین میزان تصادفی بودن
فهرست
چکیده 3
مقدمه 3
روش رمزنگاری سیگنالهای مغزی براساس پیشنهادآشوب 5
نتایج آزمایشات 8
آنالیز تصادفی 8
تجزیه و تحلیل سیگنال eeg 11
انالیز همبستگی 12
تحلیل چگالی طیف توان 14
نتیجه گیری 16
نتایج شبیه سازی 17
منابع 28
چکیده:
یک سیگنال الکتروانسفالوگرام(eeg) شامل اطلاعات حساس شخصی است که نیازمند قانونی است تاجلوی دسترسی های غیرمجاز را بگیرد.
به طور مثال HIPAA در ایالات متحده آمریکا،مستلزم آن است که دسترسی به اطلاعات شخصی بهداشتی محدود باشد تابه افراد درستی اجازه دسترسی داده شود.
در این مقاله یه روش رمزنگار بر مبنای آشوب ارائه شده است تا امن کند دیتای eeg بیمار را قبل از ارسال از یک کانال ناامن.روش پیشنهادی از یک مالتی پلکسر استفاده میکند تابه صورت دینامیکی بین دو جریان بیتی تصادفی کوانتیزه برای تولید کلید امنیت،انتخاب کند.
این روش شبیه سازی شده و برای رمزنگاری دیتای eeg و خواص آماری همچون توزیع سیگنال،خود همبستگی و cross-correlation،چگالی طیف توان، residual Deviationسیگنال اصلی و رمزنگاری شده مورد بررسی قرار گرفته شد.
نتایج تجربی بررسی میکندکه روش پیشنهادی امنیت بالایی دارد و برای حفاظت از اطلاعات حساس eeg مناسب است
مقدمه:
تله مدیسین اکنون به عنوان یک نقش بسیار مهم در بهداشت و درمان دارد.
در حقیقت بنابر مطالعات N. Lasierra et al ،98% بیمارانی که در اسپانیااز از راه حل های تله مدیسین استفاده میکردند،از آن راضی بوده اند،در حالیکه 75%آن را به روش های مرسوم ترجیح میدهند.
سیگنال های پزشکی eeg از 1950 به منظور مانیتور کما،dementiaومشکلات بلندمدت حافظه مورد استفاده قرار میگرفته است.
دیتای eeg برای هر بیمار اختصاصی است،اما وقتی در یک بیمارستان ثبت میشوند معمولا از طریق یک کانال ناامن ارسال میگردند.
از نظر قانونی حفاظت از جلوگیری از دسترسی های غیرمجاز افرادقبل از اینکه از طریق کانال ناامن ارسال گردد.
عواقب ناشی از دسترسی غیر قانونی و اصلاح اطلاعات فراوان است،به خصوص شاید موارد مربوط به حق بیمه یا وقتی که مربوط به مرگ مغزی است.
پایبندی به قوانین و مقررات،نیازبه جایگذاری یک روش رمزنگاری قوی به منظور حفاظت از اطلاعات بهداشتی بیمار را قبل از انتقال به وجود می آورد.
در سالهای اخیر،پیشرفت های قابل توجهی در زمینه استفاده از تئوری آشوب در رمزنگاری وجودداشته است.
یک سیستم آشوب گونه دارای چندین ویژگی رمزنگاری مطلوب است که آن را برای ارتباط امن ایده ال میسازد،که از جمله مهمترینشان،حساسیت به شرایط اولیه،غیرتناوبی و تصافی بودن است.
به هرحال،به خاطرتشابه خواص سیستمهای آشوب و روش های رمزنگاری،آنها نشان داده اند که به خوبی در هماهنگی در ارائه ی قوی راه حل های امنیتی بر مبنای آشوب کارمیکنند و از آنها برای حفاظت از تصویر،گفتار،صداو سیگنال های ویدیویی استفاده میشود.
دراین مقاله،یک روش مبتنی بر مپ لورنز برای حفاظت از دیتای eeg بیمار پیشنهاد شده است .
به منظورارتقاء روش پیشنهادی سیستم گسسته متغیره لورنز به صورت تصادفی کوانتیزه شد ودوتابع بولی رمزنگاری بااستفاده از متغییرکوانیزه شده ی بولی محاسبه گردید.
علاوه برآن،کلید تولید فرآیند به صورت تصادفی و توسط یک مالتی پلکسرکه به صورت غیرپریودیک بین مقداری که با توابع بولی به دست آمده است،سوییچ میکند، ساخته شده است.
بررسی نتایج شبیه سازی طرح پیشنهادی،امنیت بالایی را برای دیتای eegبیماران فراهم میکند.
II.روش رمزنگاری سیگنالهای مغزی براساس پیشنهادآشوب
یک بلوک دیاگرام شماتیک ازروش جدید در تصویر1 نشان داده شده است.
سیستم لورنز سه بعدی برپایه ی طرح پیشنهادی استفاده شده است.معادلات حاکم برآن به شرح زیر است:
همه جاx,y,z مقادیرحقیقی متغییرهای حالت سیستم لورنز هستند.
σ عددPrandtl وr عدد رایلی است.
برای مقادیر σ=10 و b=8/3 و برای همه ی مقادیر r>24.74 دینامیک چرخه ی سیستم لورنز در فضای آشوب است.
باتوجه به پیچیدگی دینامیک سیستم لورنز،دنباله ی آشوبی تولید شده غیرقابل پیش بینی تر از دنباله های آشوبی بدست آمده از سیستم های تک بعدی است.
سیستم آشوبگونه ی لورنز از یکپارچه سازی عددی برای بدست آوردن مقادیرحقیقی دنباله ی آشوب و روش Runge-Kutta-4 استفاده میکند تا بتواند برای حل معادلات دیفرانسیل 3بعدی لورنز اعمال شوند.
بنابراین برای هر تکرار روش Runge-Kutta-4 پیش پردازش مقادیر حقیقی متغیرهای حالت بدست آمده انجام شد وشامل مراحل زیر است:
1.برای هرمتغییر،شیفت راست ممیز مبناتوسط تعداد کمی از مکان ها و استخراج قسمت اعشاری برای بهبود دنباله ی شبه تصادفی
این میتواند توسط فرمول زیر به دست آید:
2.ارزش کسری شبه تصادفی dx,dy,dz در 10^14 ضرب میشودبرای بدست آوردن عدد صحیح تصادفی مربوطه ix,iy,iz:
3.این اعداد صحیح شبه تصادفی با پارامتر کوانیزه شده ی تصادفی تولیدشده N،در طول هر تکرار کوانتیزه میشودتا دنباله ی شبه تصادفی Bx,By,Bz هر Nبیت مرتبط با مقادیر حقیقی متغییرهای حالت x,y,z سیستم لورنز.
همه جا L=2^N است که تعداد سطوح کوانتیزیشن را در تکرار فعلی گزارش میکند.
مقادیرNمیتواند از 1تا 10 متغییر باشد واز فرمول زیر به دست می آید:
خروجی فرآیند کوانتیزیشن تصادفی بلوک های Bx,By,Bz به طول Nبیت است.
در هرتکرار مقدار جدید N دریافت میشوددر نتیجه با اضافه کردن تصادفی به فرایند رمزنگاری،امنیت و نیرومندی روش رمزنگاری را بهبود میبخشد.
بلوک های شبه تصادفی دودویی Bx,By,Bz برای محاسبه 1φ و 2φ با استفاده از 2تابع متعادل بولی f1,f2 استفاده شدند.
همه جا اپراتور xor است و همچنین “.” تابع اپراتور AND منطقی است.
توابع بولی f1,f2 رشته های φ1,φ2 را که ورودی مالتی پلکسر است را تولید میکنند که آن هم در نهایت رشته رمزی K را ایجاد میکند.
حداقل بیت به عنوان خط انتخاب Selبه کار گرفته میشود.
در ابتدا Sel=0و هرزمان که sel صفر باشد خروجی مالتی پالکسر φ1 است در بقیه موارد خروجی φ2 خواهد بود.
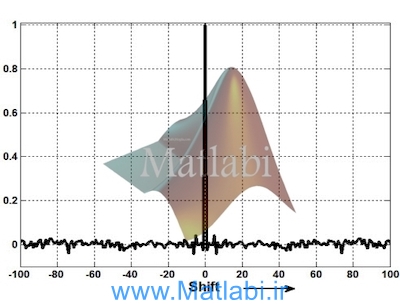
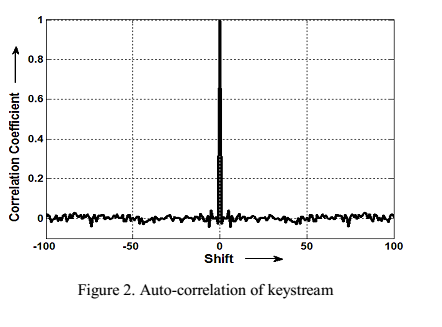
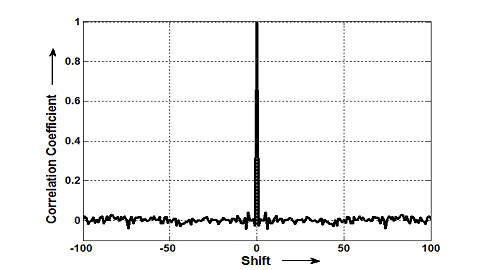
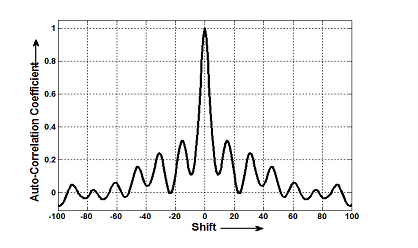
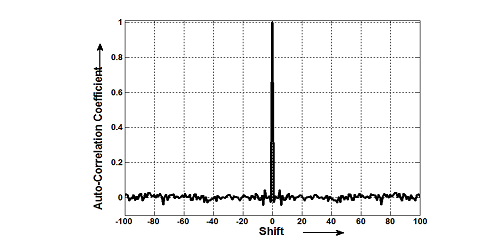
تابع خودهمبستگی رشتهk بدست آمده در شکل-2 نمایش داده شده است.
شباهت شکل آن به یک تابع ضربه درجه بالای تصادفی بودن فرایند تولیدرا نشان میدهد.
Figure 1 تابع خودهمبستگی رشتهk بدست آمده
رشته کلیدهارا به صورت گزارش میکنیم.دنباله بیت رمزی شده به صورت زیر به دست می آید.
همه جامنظور از ،سیگنال خام است وهمینطور منظور از
سیگنال رمزنگاری شده است.
برای اهداف آزمایشات و شبیه سازی ها،روش پیشنهادی رمزنگاری از دیتادانشگاه Bonn استفاده کردیم.
شرایط اولیه و پارامترهای کنترل برای آزمایشات به این شرح هستند:
σ =10,r=28, b=8/3, x(0)=13.3604 , y(0)=7.2052 , z(0)=21.5026,h=0.001
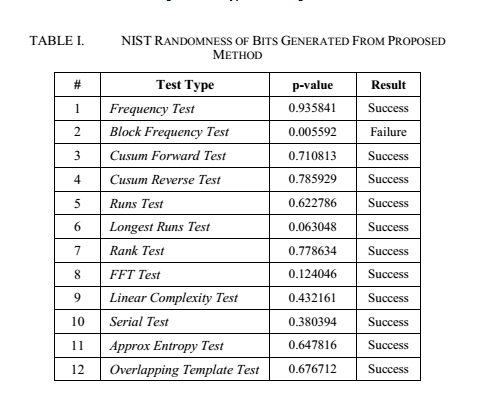
برای ارزیابی اتفاقی دنباله بیتی تولید شده،تجزیه و تحلیل از خروجی دنباله تصادفی پیشنهادی با استفاده ازبسته ی ازمون NIST(National Institute of
Standards and Technology) انجام شد.
در این تست درجه اهمیت یا همان α روی 0.01 تنظیم شده است و P-value که مربوط است به اینکه با چه احتمالی دنباله زیر تست تصادفی است ،به دست می آید.
آزمون به اینصورت است که،تست با موفقیت سپری میشود اگر مقدار p-value به دست آمده از مقدارα بزرگتر باشد.
مقدارα برابر با 0.01 مشخص میکندکه یکی در 100 دنباله برای بازگشت مورد انتظاراست و p-value بزرگتراز 0.01 میگوید که دنباله بااطمینان 99% تصادفی است.
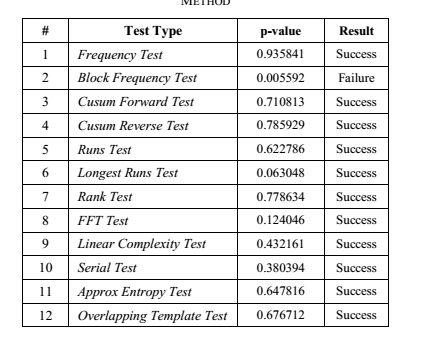
نتایج این تست های آماری در جدول1 نشان داده شده است.
میتوان مشاهده کرد که همه تست ها جز یکی از آنها،سپری شده اند.
این بسیار مهم است که توجه داشته باشید که عملکردخوب روش ارائه شده در این آزمونها هیچ تضمینی از ارتباطات امن ندارد و تنها یک شاخص از عملکرد مورد انتظار است.
Table نتایج این تست های آماری
برای روشن سازی این تست ها،توضیحات کوتاهی درباره ی انها بیان کردیم:
تست فرکانسی: تمرکز این تست بر روی نسبت صفر ها و یک ها ، برای تمام دنباله می باشد.
هدف این تست این است که می خواهیم ببینیم تعداد صفر ها و یک ها در دنباله تقریبا شبیه به یک دنباله با مقادیر تصادفی هست یا خیر .
-تست فرکانسی بلوکی :
تمرکز این تست بر روی تناسب یک ها در داخل یک بلوک m بیتی است.
هدف این تست تشخیص فرکانس یک ها در بلوک های m بیتی است.
این فرکانس در یک بلوک با مقادیر تصادقی تقریبا M/2 است . ( اگر M=1 شود ، تست مونوبیت محاسبه می شود ) .
Cosum –test تست جمع های انباره ای :
این تست بر مبنای مقدار ماکزیمم مطلق در جمع های جزئی ِ دنباله است .
مقادیر بزرگ این آمار نشان دهنده ی تعداد زیادی یک یا صفر در قسمت اولیه ی دنباله است .
و مقادیر کوچک نشان دهنده ی آن است که صفر ها و یک ها به صورت هموار در هم آمیخته شده اند .
-تست Runs :
تمرکز این تست بر روی تعداد عددهای runs در دنباله است .
هر جا که یک run هست دنباله بدون وقفه بیت های یکسان دارد.
یک run ِ طول ِ k شامل دقیقا k بیت یکسان است و یک بیت قبل و بعد آن بیت مقابل آن است . ( اگر ران صفر باشد ، مرزها یک می شوند ) .
تست طولانی ترین ران ( سلسله )
تمرکز این تست بر روی این است که طولانی ترین سلسله یک ها را در بلوک های Mبیتی پیدا کند .
هدف این تست تشخیص جایی است که طولاتی ترین سلسله یک ها در دنباله ی تست شده با طول بلند ترین سلسله یک ها( که قابل انتظار است ) در دنباله ی تصادفی سازگار باشد .
– تست رتبه
تمرکز این تست روی رتبه ی زیرماتریکس های منفصل در سر تا سر رشته است .
هدف این تست بررسی وابستگی خطی در میان زیر رشته های طول ثابت، در دنباله ی اصلی است
تست تبدیل فوریه :
تمرکز این تست بر روی ارتفاع پیک ها در تبدیل فوریه ی دنباله ی مورد ِ بررسی است .
هدف این تست تشخیص ویژگی های پریودیک( الگوهای مکرر ) در رشته ی تست شده است که اختلاف رشته ی تست شده را با فرض اتفاقی بودن بررسی می کند.
تست پیچیدگی خطی :
تمرکز این تست بر روی طول شیفت رجیستر بازخورد خطی است.
انجام پروژه متلب با متلبی
هدف این تست تشخیص این است که رشته نسبت به مقادیر تصادفی ، دارای پیچیدگی هست یا خیر ؟
-تست سریال :
تمرکز این تست بر روی فرکانس همه ی الگوهای M بیتی روی هم افتاده ی ممکنه است .
هدف این تست تشخیص این است که آیا تعداد رخداد ها 2^m ، الگوهای روی هم رفته ی m بیتی ، تقریبا شبیه به چیزی است که برای رشته ی تصادفی انتظار داشتیم یا خیر .
تست بی نظمی تقریبی
مثل تست سریال ، تمرکزش بر روی تکرار الگوهای m بیتی روی هم افتاده ی ممکنه در سرتاسر رشته است .
هدف این تست مقایسه ی فرکانس بلوک های روی هم افتاده ی دو طول ( پی در پی یا نزدیک هم مثل m و m+1 ) در مقابل نتیجه ی قابل انتظار برای رشته ی تصادفی است .
– تست تطبیق الگوهای روی هم افتاده ( دارای اشتراک )
تمرکز این تست روی تعداد رخداد های رشته ی هدف ِ از پیش تعیین شده است.
در پنجره های m بیتی به دنبال یک الگوی ام بینی تعیین شده می گردد .
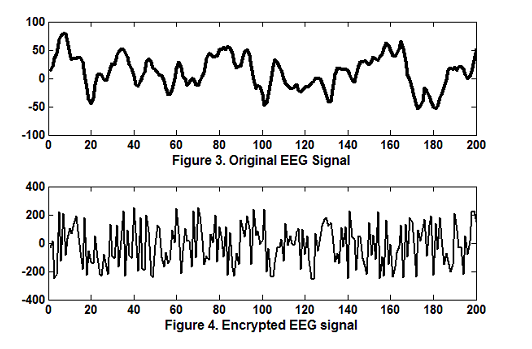
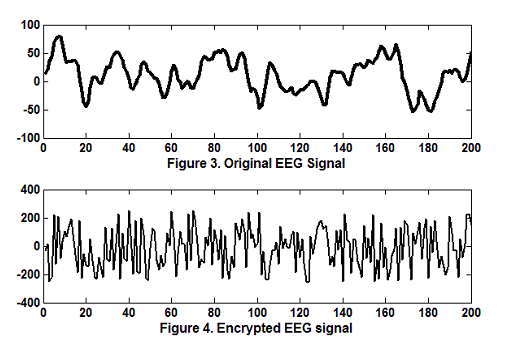
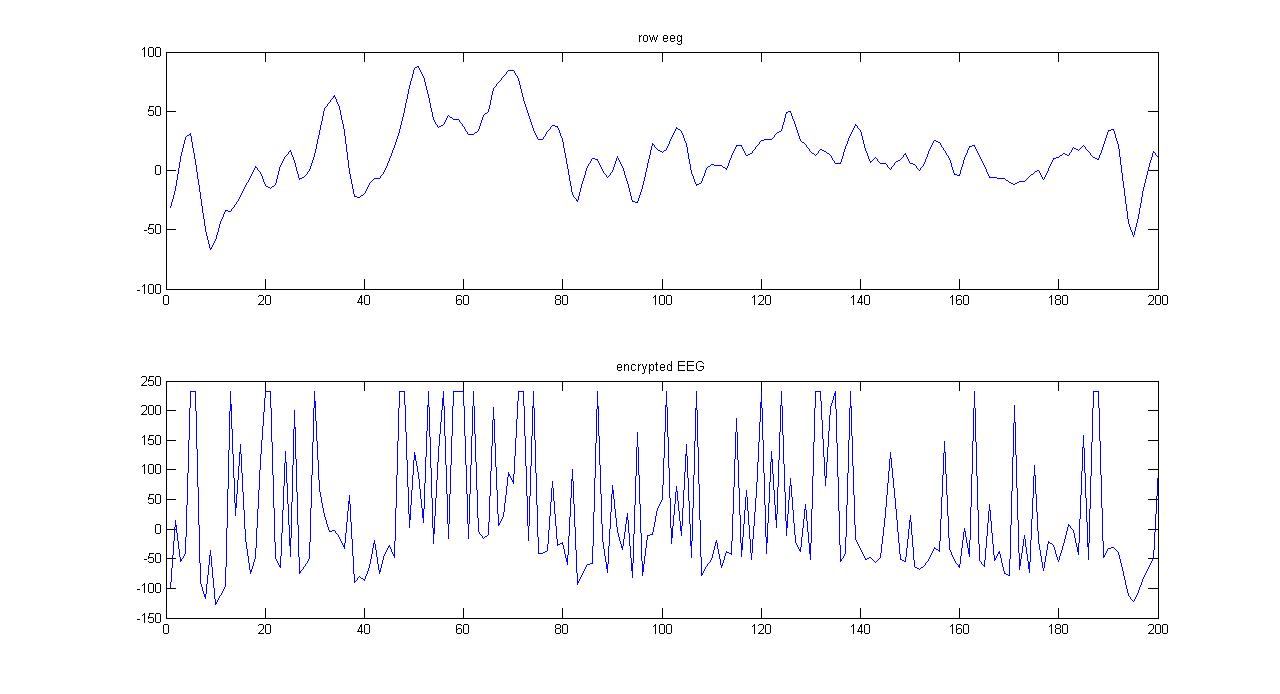
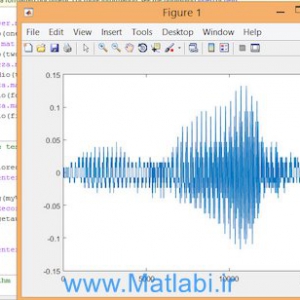
سیگنال eeg خام و همینطور سیگنال رمزنگاری شده در تصویر زیر نشان داده شده اند
سیگنال رمزی شده بسیار شبیه به نویز میباشد که ماهیت تصادفی خودش را نشان میدهد.
Figure 2سیگنال eeg خام و همینطور سیگنال رمزنگاری شده
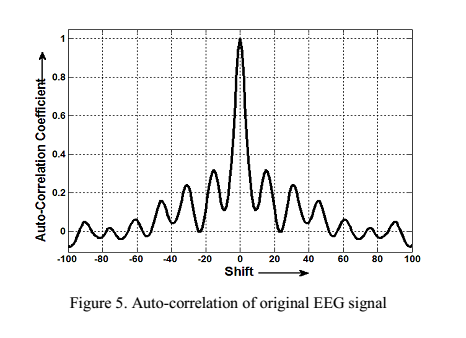
خودهمبستگی سیگنال مقدارشباهت سیگنال به نسخه تاخیر یافته ی خودش است.
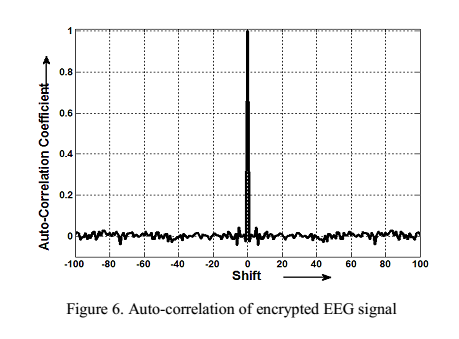
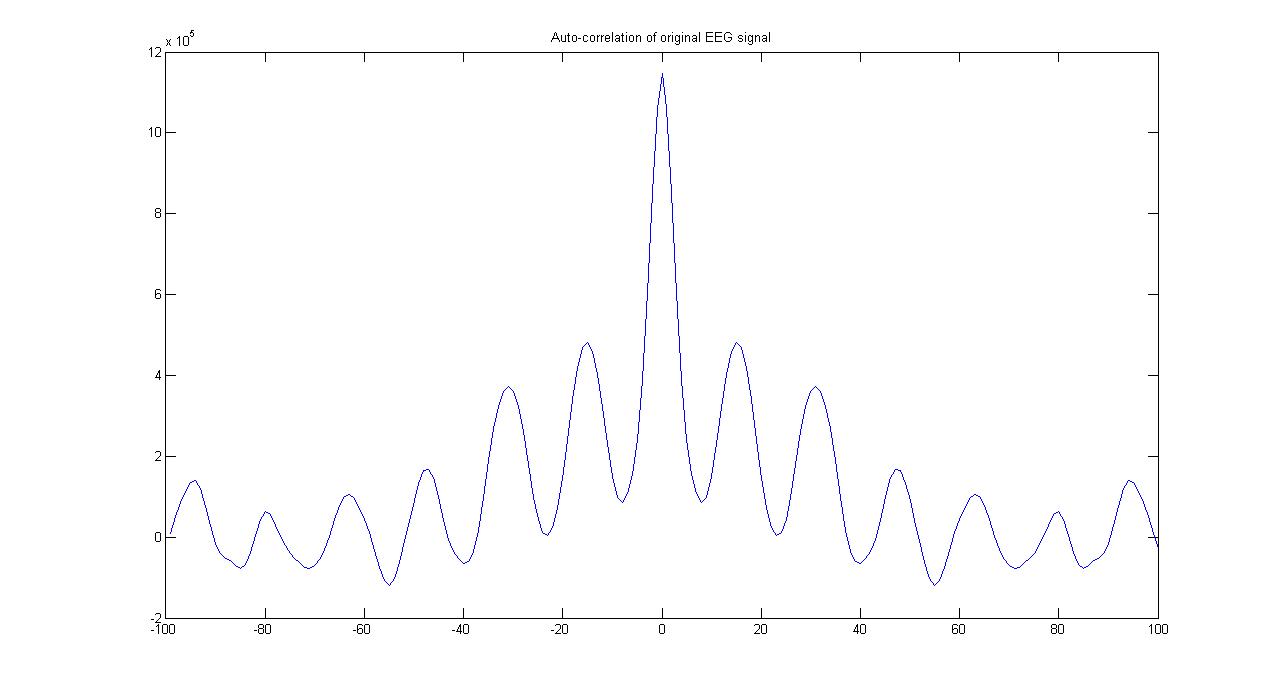
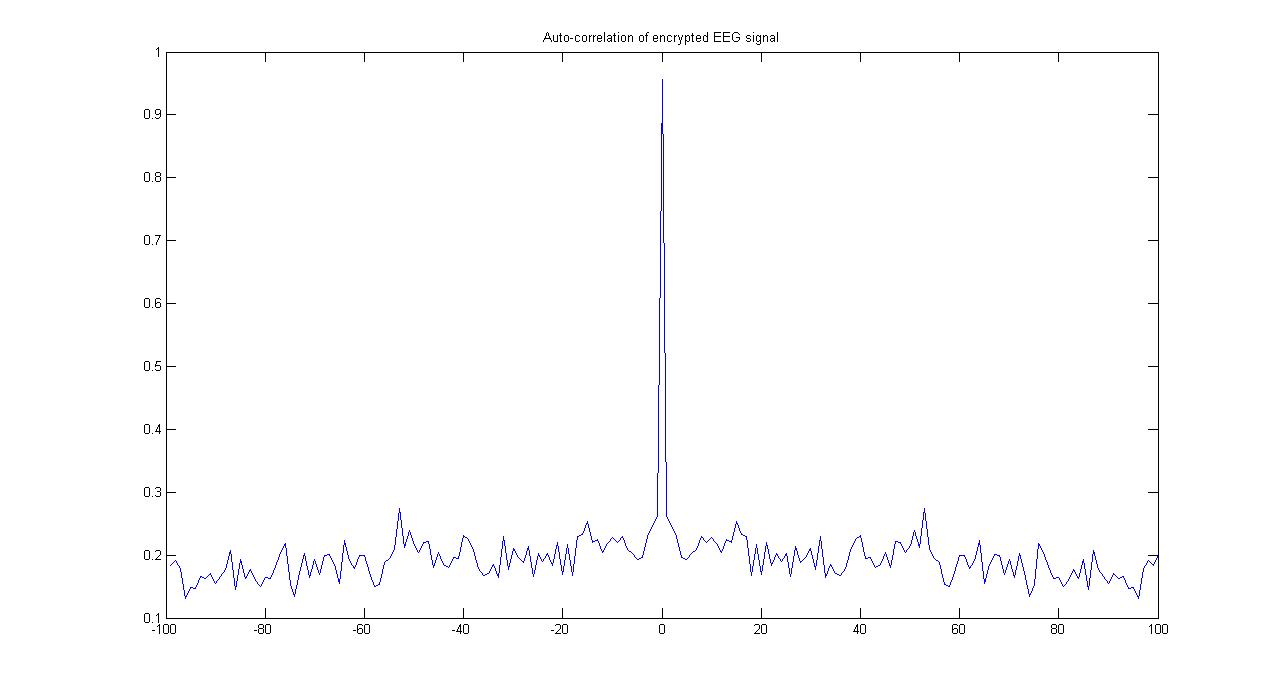
تابع خودهمبستگی سیگنال اصلی و سیگنال رمزی شده در زیر نشان داده شده است.
برای سیگنال اصلی خودهمبستگی اش نشان میدهد که آیا تابع خودهمبستگی سیگنال رمزی مقادیری کوچکترازشیفت صفر(لگ صفر) دارد،مقادیر کم همبستگی ،درجه بالایی از تصادفی بودن را نشان میدهد.
Figure 3 خودهمبستگی سیگنال
Figure 4 تابع خودهمبستگی سیگنال رمزی شده
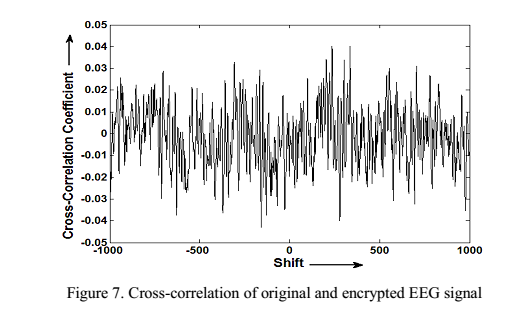
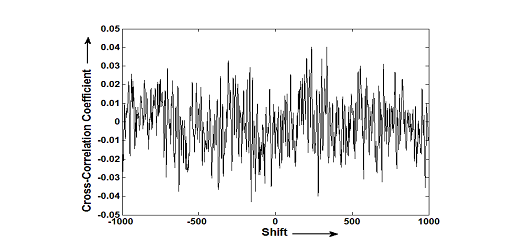
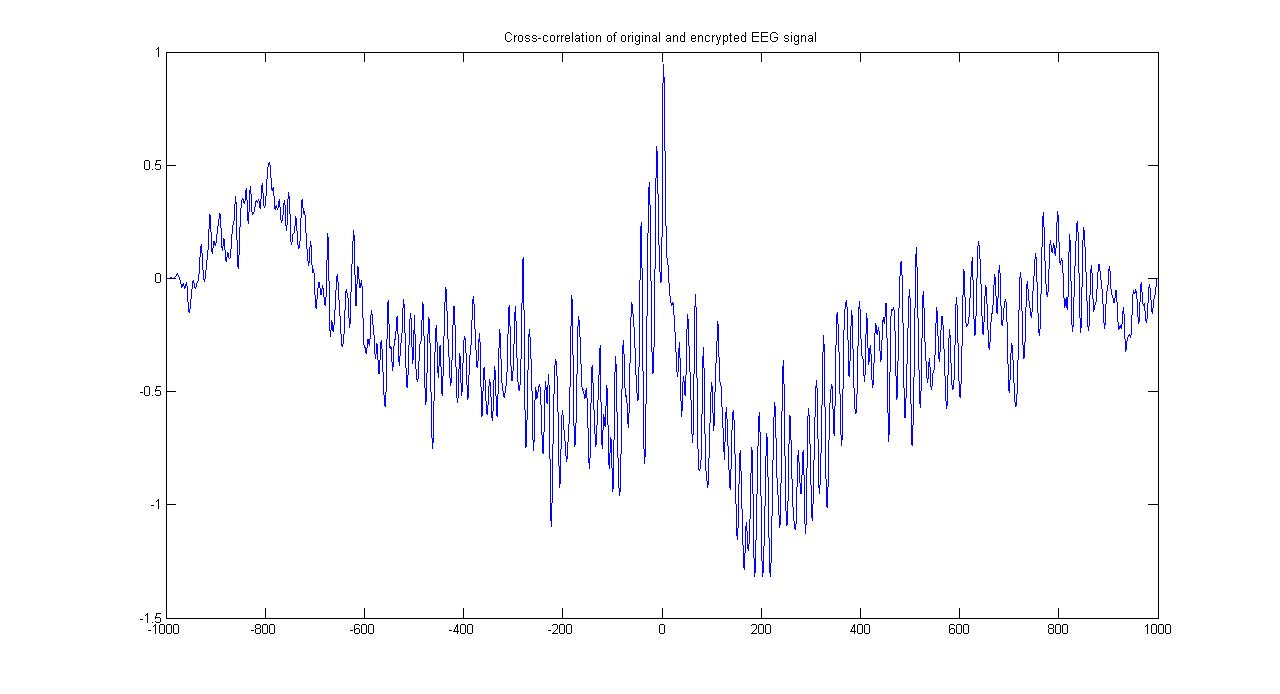
همبستگی بین سیگنال اصلی و سیگنال رمزی شده در تصویر زیر نمایش داده شده است
Figure 5 همبستگی بین سیگنال اصلی و سیگنال رمزی شده
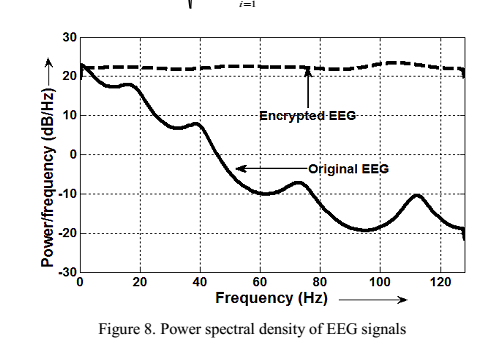
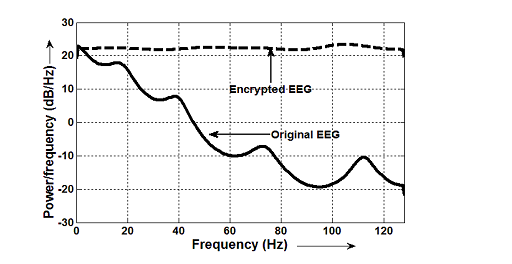
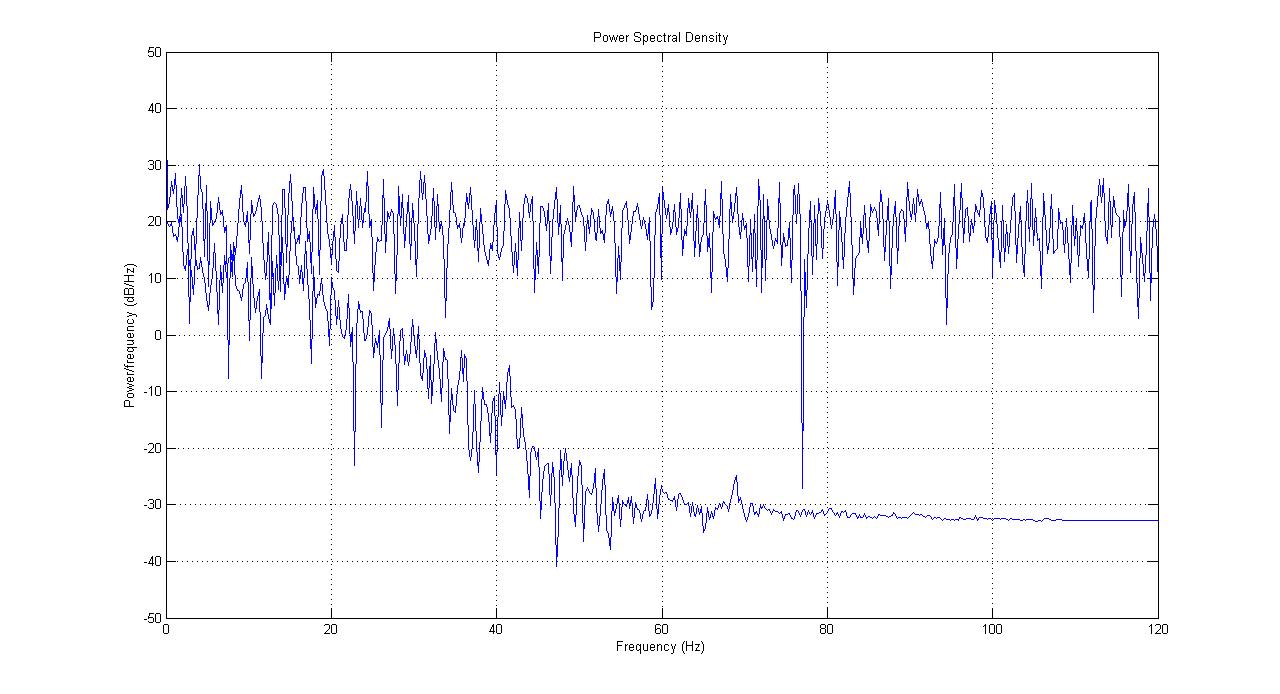
چگالی طیف توان یا (PSD)،فرکانس غالب حاضر در سیگنال را نشان میدهد.
برای کیفیت خوب رمزنگاری،سیگنال رمزنگاری باید در همه فرکانس هامقادر مشابه داشته باشد،تا حدودی شبیه به باند نویز سفید است.
چگالی طیف توان در زیر نمایش داده شده است.
Figure 6چگالی طیف توان
برای سیگنال اصلی که فرکانس غالب در رنج
0-20 hz است اما کمترین انرژی در فرکانس های بالاتر است.
سیگنال رمزنگاری شده ویژگی هایی مشابه نویز دارد و دارای چگالی صاف است.
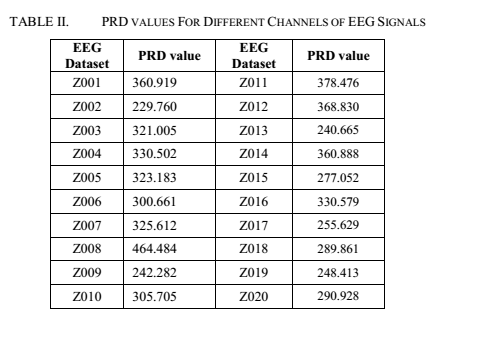
E.آنالیز درصد انحراف باقی مانده
برای تعیین میزان که سیگنال رمزنگاری شدهC(i) متفاوت ازسیگنال اصلی E(i) است.
پارامتر PRD یا درصدانحراف باقی مانده محاسبه میشود.
این اندازه گیری های متفاوت سیگنال اصلی وسیگنال رمزنگاری شده را فراهم میکند و به صورت زیر محاسبه میشود:
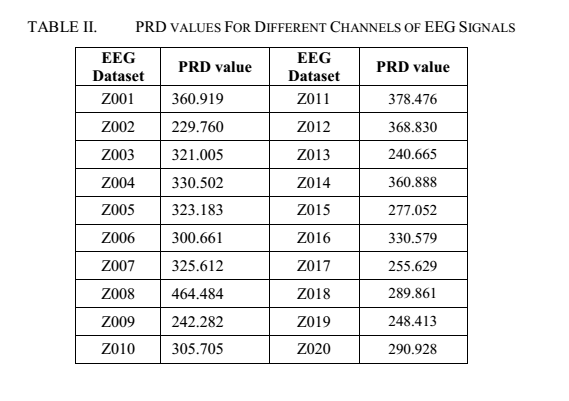
مقادیرPRD برای بیست کانال اول سیگنال اصلی و سیگنال رمزنگاری شده محاسبه گردید.
Table مقادیرPRD
به منظور ارائه شرایط مناسب برای تشخیص در محیط های سلامت،در اغلب موارد کنترل اطلاعات بیمار از موارد غیرمجاز اجباری است.
در این کار، با جایگذاری یک روش رمزنگاری سیگنالeeg که از ویژگی های سیستم 3بعدی آشوب گونه لورنز استفاده میکند.
که متغییرهای حالت نشان دهنده ی ویژگی های تصادفی و غیرمتناوب است.
تکنیک همچنین دارای یک تکنیک کوانتیزیشن است که قدرت بیشتری را به سیستم رمزنگاری می افزاید.
این روش با یک پایگاه داده استاندارد eeg تست شد.
نتایج نشان میدهد که روش رمزنگاری پیشنهادی امنیت بالایی را به نمایش میگذارد و برای حفاظت از اطلاعات حساس بیماران مناسب است
نتایج شبیه سازی:
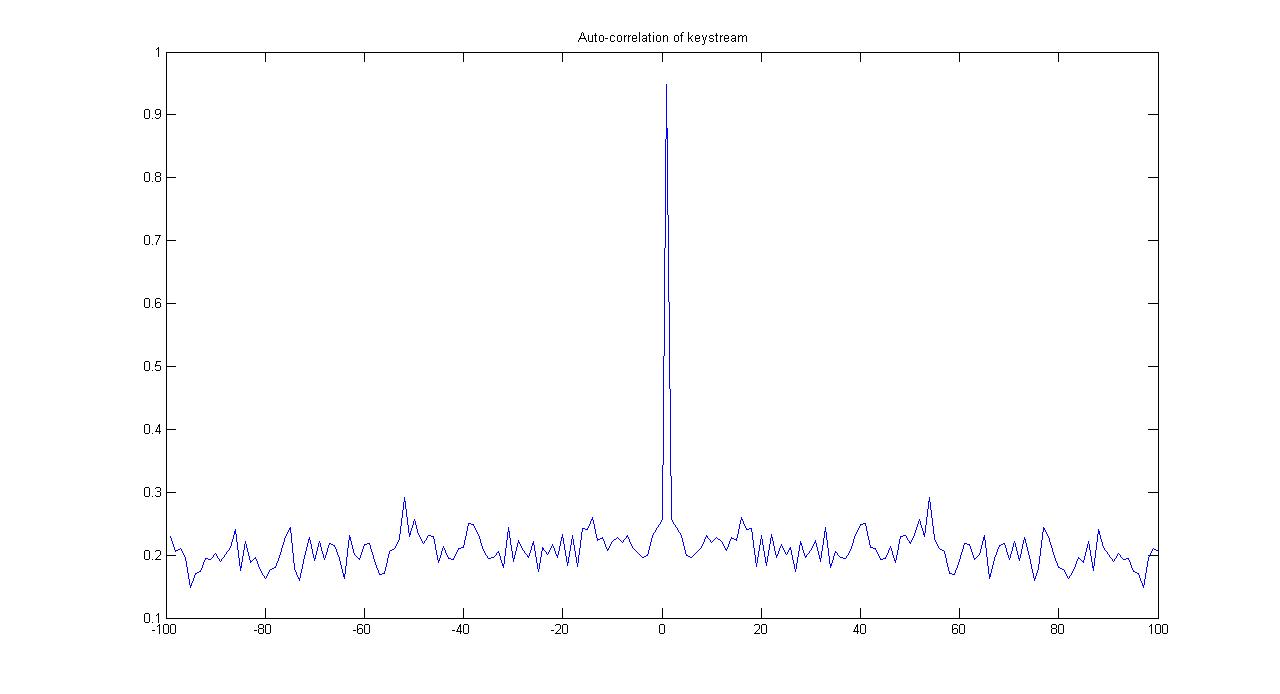
شکل1) تابع خودهمبستگی برای رشته keystream
Figure 7 تابع خودهمبستگی شده در شبیه سازی
Figure 8 تابع خودهمبستگی شده در شبیه سازی حاصل شبیه سازی ما
Figure 9 نمونه ی سیگنال خام وسیگنال رمزنگاری شده در مقاله
Figure 10 سیگنال خام استفاده شده در شبیه سازی و سیگنال رمزنگاری شده حاصل از شبیه سازی
Table تست های تصادفی مورد استفاده در مقاله
Table 4 نتایج تستهای تصادفی ما در شبیه سازی
| Result | p-value | Test Type | # |
| Success | 0.8432 | Frequency Test | 1 |
| Failure | 0.0018 | Block Frequency Test | 2 |
| Success | 0.5438 | Cusum Forward Test | 3 |
| Success | 0.5712 | Cusum Reverse Test | 4 |
| Success | 0.8565 | Runs Test | 5 |
| Success | 0.1291 | Longest Runs Test | 6 |
| Success | 0.7675 | Rank Test | 7 |
| Success | 0.2111 | FFT Test | 8 |
| Success | 0.5001 | Linear Complexity Test | 9 |
| Success | 0.3156 | Serial Test | 10 |
| Success | 0.6593 | Approx Entropy Test | 11 |
| Success | 0.4597 | Overlapping Template Test | 12 |
Figure 11تابع خودهمبستگی سیگنال اصلی
Figure 12تابع خودهمبستگی سیگنال اصلی در نتایج شبیه سازی
Figure 13تابع خودهمبستگی سیگنال رمزنگاری شده مورداستفاده در مقاله
Figure 14 تابع خودهمبستگی سیگنال رمزی حاصل شده
Figure 15 )تابع همبستگی دوسیگنال اصلی ورمزنگاری شده در مقاله
Figure 16تابع همبستگی سیگنال اصلی با سیگنال رمزنگاری شده به دست امده از نتایج
Figure 17چگالی طیف توان موجود در مقاله
Figure 18تابع چگالی طیف توان به دست امده از شبیه سازی
Table مقادیر PRD حاصل شده در مقاله
Table 6مقادیر PRD بدست امده در شبیه سازی
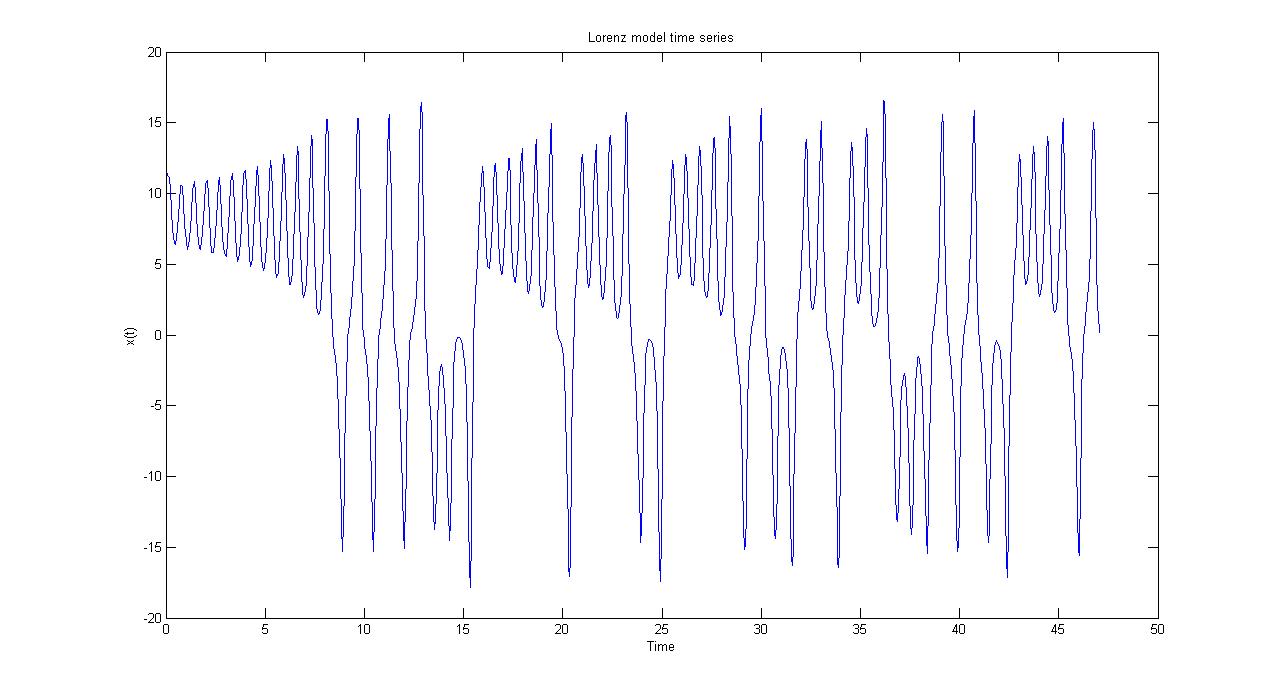
Figure 19 ترژکتوری لورنز
Figure 20یکی ازتوابع لورنز(x)
منابع:
[1].Musheer Ahmad and et,” Chaos-based Encryption of Biomedical EEG Signals using Random Quantization Technique”, 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI)
[2]. R. G. Andrzejak, K. Lehnertz, C. Rieke, F. Mormann, P. David, C. E.
Elger, Indications of nonlinear deterministic and finite dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state, Physical Review E, Vol. 64, 2001, pp. 061907-8.
[3].http://epileptologiebonn.de/cms/front_content.php?idcat=193&lang=3&changelang=3
[4]. Andrew Rukhin and et,” A Statistical Test Suite for
Random and Pseudorandom Number Generators for Cryptographic Applications”, NIST Special Publication 800-22
Revision 1a
کلید واژه : آشوب,پروژه متلب,شبیه سازی با متلب,matlab project,پروژه های matlab,
Chaos system, EEG signals, encryption, security, random quantization
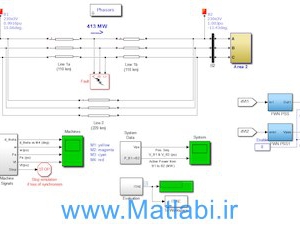
شبیه سازی مقاله
Chaos-based Encryption of Biomedical EEG Signals using Random Quantization Technique
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.