توضیحات
An Efficient Transient Analysis Algorithm for Mildly Nonlinear Circuits
ترجمه فارسی موضوع مقاله: روش آنالیز بازده گذرای جدید برای مدارهای غیر خطی میلدلی
دارای ترجمه در قالب ورد است.
گزارش کار:
در این مقاله روش آنالیز بازده گذرای جدید برای مدارهای غیر خطی میلدلی ارائه شده است.
این روش مبتنی بر سری های ولترای مدارهای غیرخطی است.
این ویژگی های مدارهای غیرخطی برای استفاده در مجموعه ای از مدارهای خطی که بنام مدارهای ولترا نامیده می شوند استفاده می شود.
ورودی مرتبه اول مدارهای ولترا با مدارهای غیرخطی برابرست، در حالی که مراتب بالاتر مدارهای ولترا از پاسخ مرتبه پایین تر این مدارها حاصل می شود.
درونیابی سری های فوریه برای تقریب ورودی های مرتبه بالاتر مدارهای ولترا بکار گرفته شده است.
این مدارها با استفاده از شبیه سازی داده های نمونه مدارهای خطی برای بازده محاسباتی وپاسخ مدارهای غیرخطی که با استفاده از فواصل زمانی مساوی بدست می آیند آنالیز می شوند.
دقت این روش توسط مراتب ولترا و درونیابی سری فوریه کنترل می شود.
منابع مختلفی برای کنترل خطا انالیز شده اند.
الگوریتم ارائه شده در این مقاله برای اجرای محاسبات شبیه سازی داده های نمونه برای مدارهای غیرخطی (SDSN) بکار می رود.
برای بررسی دقت و بازده این روش، الگوریتم PC مرتبه اول با استفاده از روش فوروارد اویلر برای پیش بینی مقادیر بک وارد اویلر اجرا شده تا الگوریتم مرتبه اول با استفاده از BDF و نیز در اجرای SDSN اصلاح شود.
چند مدار غیرخطی با استفاده از SDSN و PC آنالیز شده و نتایج نمایش داده شده است.
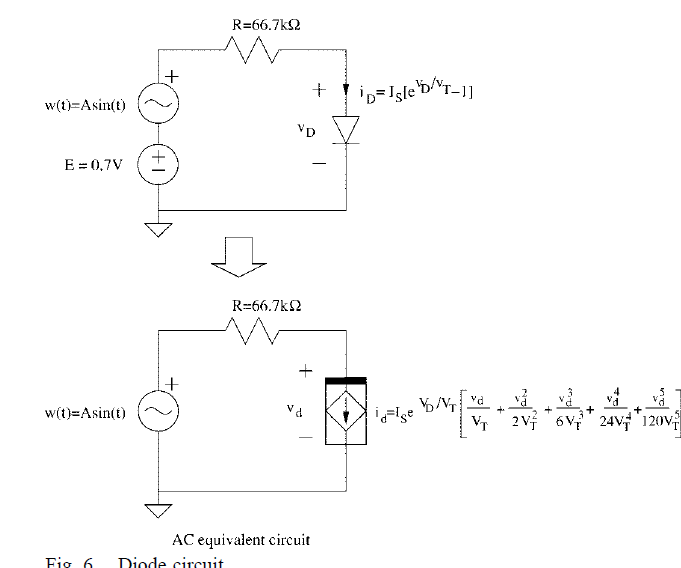
- مدار دیودی:
مدار دیودی نشان داده شده در شکل 6 را در نظر بگیرید.
مشخصات دیود بدین شرح است: ، که IS=10-16 A و Vt=26mV در 300K. نقطه کار dc با حل مدار از روش تکرار نیوتن-راپسون بدست می آید.
روابط مدار در m-file به نام dSovleNLA.m نوشته شده است. پس از اجرای این برنامه داریم:
در آنالیز SDSN، عرض پنجره شبیه سازی روی 0.1 دوره تناوب سیگنال تنظیم می شود، برای مثال 0.1s.
تعداد نمونه های انتخاب شده در پنجره ی شبیه سازی در آنالیزPC ,100تاست.
این مسئله باعث کاهش تعداد مراحل در نتیجه ی خطاهای بزرگ می شود.
تعداد مراحل در پنجره ی شبیه سازی در SDSN ,20تاست.
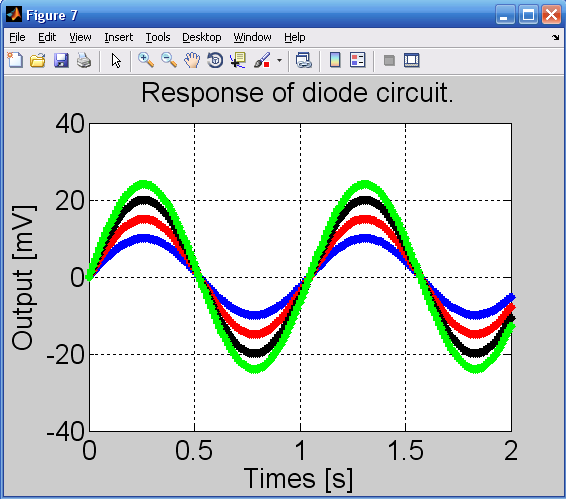
معیار اتمام آنالیز نیوتن-راپسون در آنالیز PC روی 10 تنظیم می شود. ولتاژ ac گذرنده از دیود با استفاده از هر دو روش SDSN و PC محاسبه شده است و نتایج برای ورودی با دامنه های مختلف در شکل 7 نمایش داده شده است.
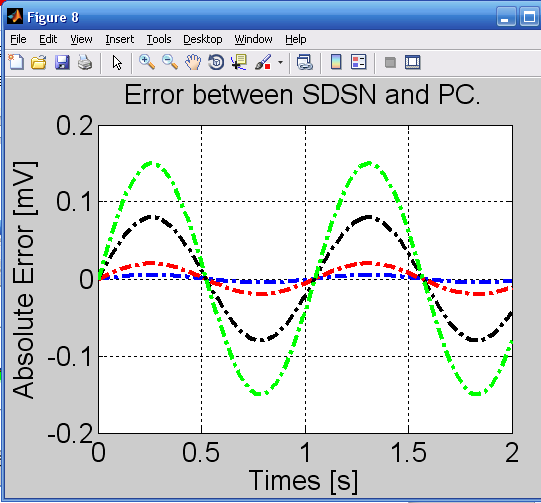
اختلاف بین SDSN و PC در شکل 8 نمایش داده شده است.
دیده می شود که نتایج SDSN با نتایج حاصل از PC منطبق است.
ماکزیمم اختلاف نرمالیزه شده 1% است.
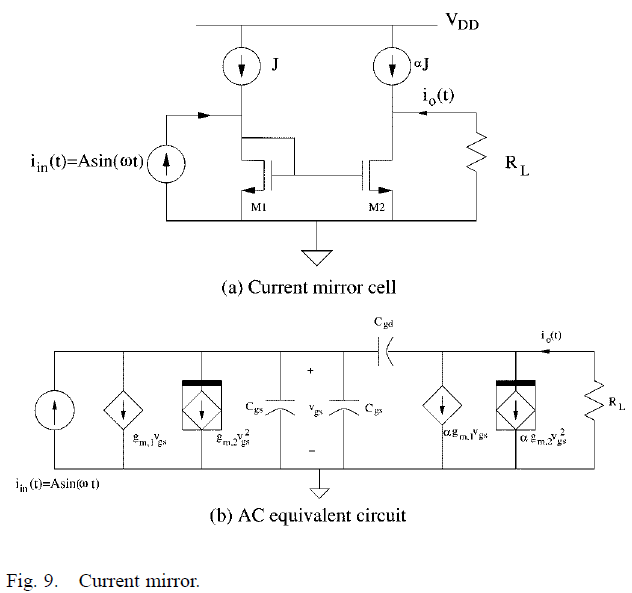
- آینه جریان:
دومین مثال به بررسی سلول آینه جریان نشان داده شده در شکل 9 می پردازد.
مانند قبل با نوشتن روابط مدار و ذخیره کردن در dSovleNLB.m پس از اجرا داریم:
مدار ac سلول در شکل 9 نمایش داده شده است.
ورودی منبع جریان سینوسی با دامنه ml1 و فرکانس GHz1 است.
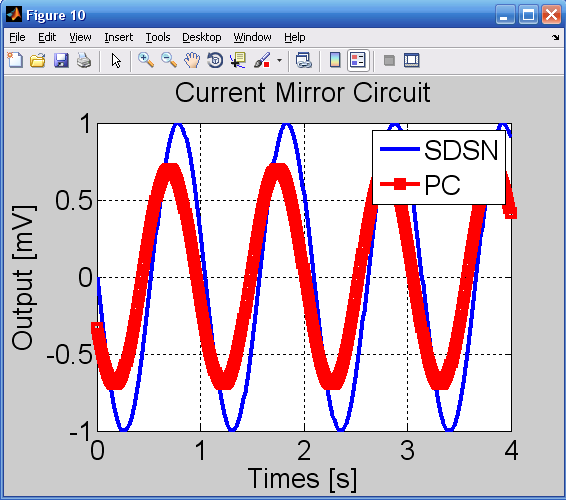
در شبیه سازی ما, جریان گین آینه α واحد است. جریان خروجی با استفاده از هر دو روش SDSN و PC محاسبه شده است.
نتایج در شکل 10 با دو فرض بودن یا نبودن خازن های گیت – سورس و گیت – درین نمایش داده شده است.
دیده می شود که وقتی از خازنها صرفنظر کرده ایم, در آینه داریم .
اما وقتی خازنها را در نظر می گیریم, جریان خروجی کاهش می یابد.
نتایج حاصل از آنالیزهای SDSN و PC با هم مطابقت دارد.
- تقویت کننده های کم نویز :
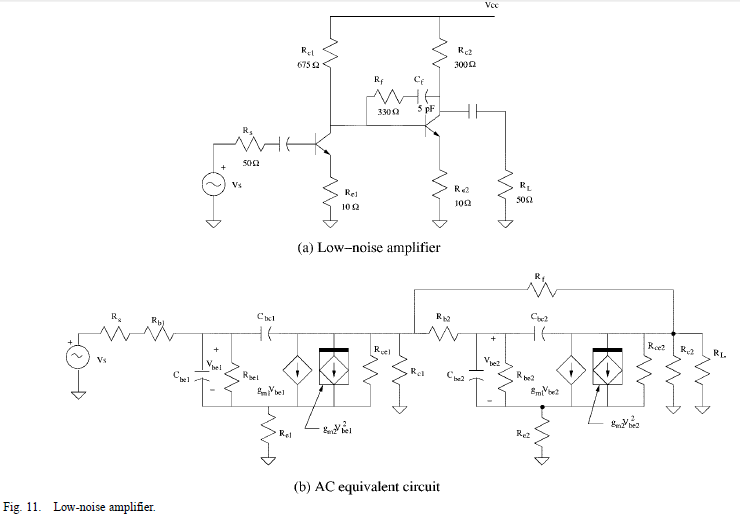
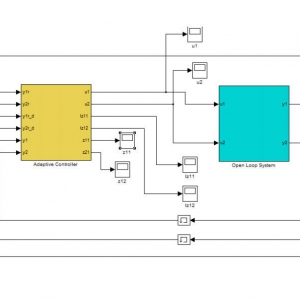
یک تقویت کننده ی کم نویز در شکل 11 نمایش داده شده است که بررسی می شود.
ورودی سیگنال ولتاژ سینوسی با فرکانس 1GHz و دامنه 1mA است.
تقویت کننده با استفاده از روش SDSN بررسی و هم زمان با روش PC مبتنی بر BDF و با استفاده از فرمول های Tableau اجرا شده است.
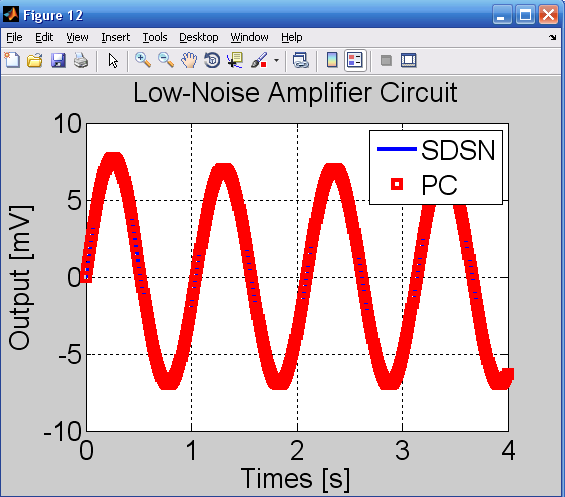
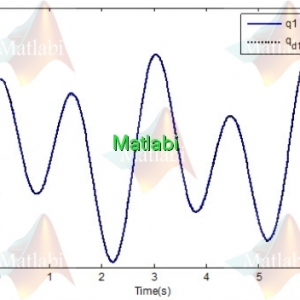
بعد از اجرای dSovleNLC.m نتایج در شکل 12 نمایش داده شده است.
مشاهده می شود در هر دو روش تطابق وجود دارد.
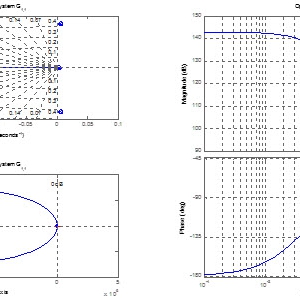
این تقویت کننده دارای ولتاژ گین حدود 16dB است.
- مدار غیرخطی با خازن:
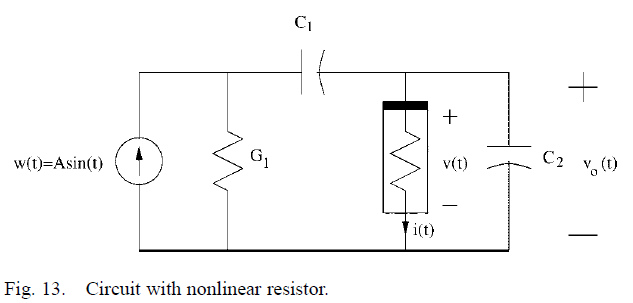
برای توضیح بیشتر این روش، مدار نشان داده شده در شکل 13 را بررسی می کنیم.
تعداد مراحل پنجره ی شبیه سازی برای SDSN و PC بترتیب 20 تا 100 تاست.
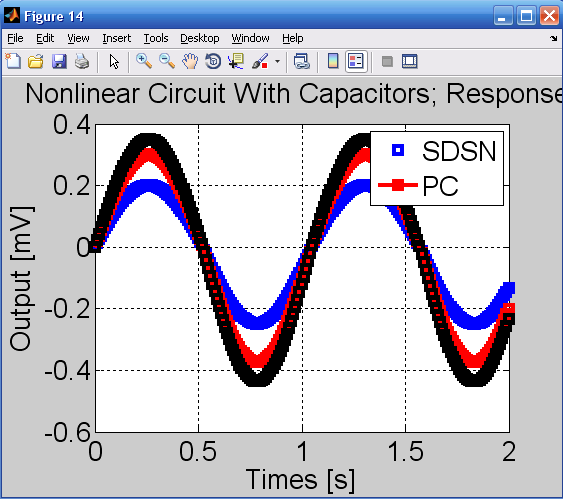
نتایج در شکل 14 برای دامنه های مختلف ورودی نمایش داده شده است.
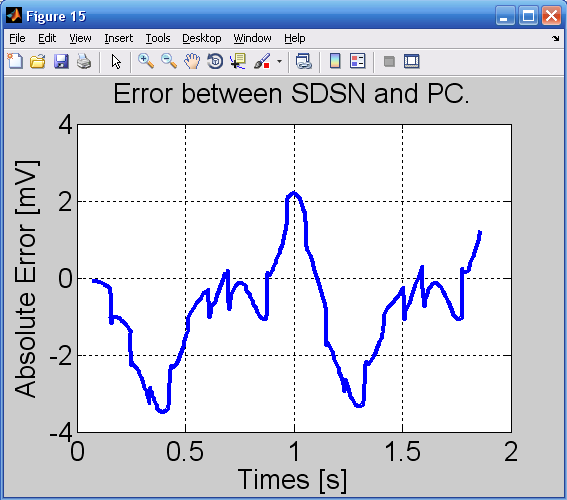
دیده می شود که نتایج حاصل از SDSN و PC در شکل 15 نمایش داده شده و حداکثر اختلاف نرمالیزه شده نزدیک به 1% است.
که برای نشان دادن تعداد مراحل شبیه سازی در آنالیز PC باید به اندازه کافی بزرگ باشد.
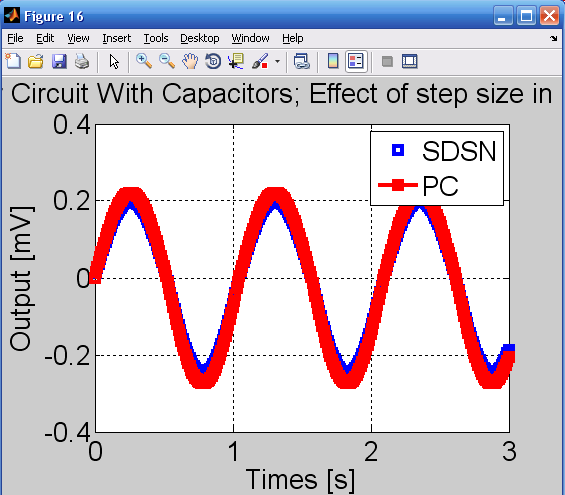
با تنظیم اندازه ی پنجره ها بر روی0.55 مدار حل شده و تعداد مراحل پنجره ی شبیه سازی برای SDSN بدون تغییر می ماند اما برای PC متغیر است.
نتایج در شکل 16 نمایش داده شده است.
مراحل کم پنجره در آنالیز PC مشهود است.
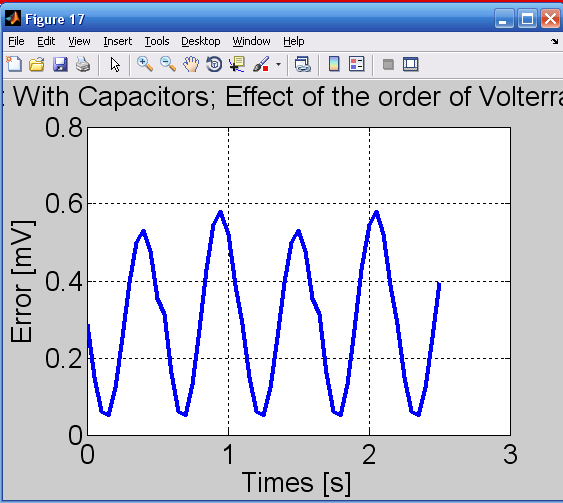
خطای ناشی از برش سری ولترا نیز بترتیب با محاسبه ی اختلاف بین پاسخ مدار با مرتبه های 3 و4 بسط سری ولترا بررسی شده است و نتایج آن در شکل 17 به ازای دامنه ی V 0.5 نمایش داده شده است.
مشاهده می شود خطای نرمالیزه شده ناشی از برش سری ولترا حدود 0.1درصد است.
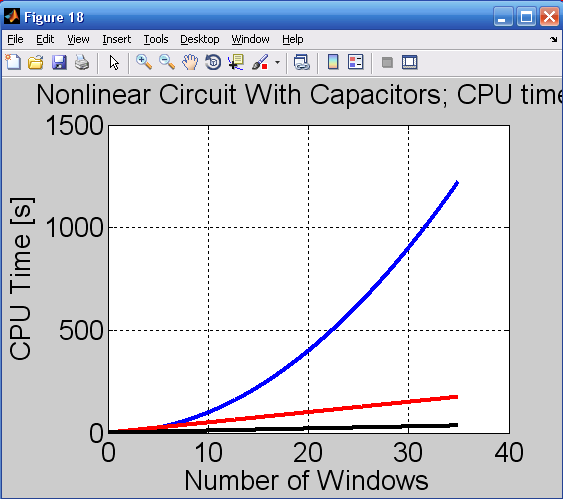
محاسبات بازده SDSNکه در آن زمان cpu برای SDSN و PC بر حسب تابعی از تعداد پنجره های شبیه سازی است در شکل 18 نشان داده شده است.
نتیجه گیری
در این مقاله, روش جدیدی برای بررسی مدارهای غیر خطی میلدلی با فواصل زمانی یکسان معرفی کردیم.
این روش مبتنی بر نمایش سری ولترا برای سیستم های غیر خطی و درونیابی سری فوریه است.
ویژگی های مدارهای غیر خطی میلدلی در مجموعه ای از مدارهای ولترای خطی با توپولوژی مشخص استفاده شده است.
این مدارها با استفاده از شبیه سازی داده های نمونه حل شده اند.
برای مقایسه با روش های SPICE-Like سنتی, روش پیشنهادی برای هر مرحله به تکرار نیوتن-راپسون یا انتگرال تصحیح پیش بینی نیاز ندارد.
در عوض, به عملگر های بردار/ماتریس و محاسبات FFT برای هر پنجره نیازمند است, که انتظار داریم به محاسبات کمتری نیاز داشته باشد، اما نه در همه ی موارد.
در آنالیز مدار داده شده الگوریتم پیشنهادی پیش محاسبه می کند مانند محاسبه ی بردار/ماتریس M و P که محاسبات کمتری نیاز دارد.
اگر ما نیاز به دانستن پاسخ مدار برای زمان های متعددی داشته باشیم که هزینه ی محاسبات اولیه ی زیادی نیاز داشته باشد در این روش بازده محاسبه می شود.
شبیه سازی های SPICE-Like، حل مدار را در هر زمان محاسبه می کند حتی اگر مدار دارای ورودی شبیه مرحله قبل باشد مانند شبیه سازی های SPICE-Like ساده که با استفاده از اطلاعات قبل دوباره محاسبه می کند.
بنابراین بین الگوریتم های SPICE-Like سنتی و روش ارائه شده در این مقاله مصالحه برقرار است.
روش پیشنهادی برای مدارهای غیر خطی با نقطه کار dc ثابت و ورودی ac کوچک مناسب است.
در این مدارها، المان های غیر خطی می توانند با استفاده از عبارات مرتبه پایین تر بسط سری فوریه در نقطه کار dc (غیر خطی میلدلی) توصیف شود.
این روش برای هر دو نوع مدارهای تک ورودی و چند ورودی مناسب است.
هرچند شکل موج های ورودی می تواند اختیاری باشد، اما بطور عمده اجرای این روش با ورودی های سینوسی ساده می شود.
دقت روش پیشنهادی ناشی از دقت الگوریتم شبیه سازی و دقت مدلینگ است.
برای مدار غیر خطی داده شده با ویژگی های غیر خطی مشخص، دقت مدلینگ را می توان قبل از شروع شبیه سازی تعیین کرد.
این مسئله اجازه می دهد مرتبه ی بسط سری فوریه در المان های غیر خطی و مرتبه ی بسط سری ولترا در مدار را تنظیم کنیم.
معمولا هر دوی این مرتبه ها یکسان هستند.
دقت شبیه سازی عمدتا بوسیله ی مرتبه ی درونیابی سری فوریه ی استفاده شده در تقریب ورودیه مدارهای ولترای مرتبه ی بالا و اندازه ی پنجره ی شبیه سازی تعیین می شود.
معمولا وقتی که الگوریتم های لاپلاس معکوس عددی مرتبه بالا استفاده می شود از خطای ایجاد شده ی ناشی از محاسبه ی M و P صرفنظر می شود.
افزایش مرتبه درونیابی سری فوریه کمتر از خطای درونیابی است بنابراین دقت بیشتر است.
هر چند، افزایش زمان محاسبات پیش پردازش ناشی از محاسبه ی بردار Pk است.
بدیهی است که باید از خطای ناشی از تاثیر Gibb، استفاده از مرتبه های خیلی پایین درونیابی بسط سری فوریه اجتناب کرد.
کلید واژه : مدارهای ولترا ,برق الکترونیک ,کامپیوتر ,مدارهای غیرخطی, Interpolating Fourier series, nonlinear circuits,transient analysis, Volterra series
شبیه سازی مقاله
An Efficient Transient Analysis Algorithm for Mildly Nonlinear Circuits
توسط مجریان سایت متلبی تهیه و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.