توضیحات
کنترل کننده تطبیقی برای سیستم های غیرخطی نامشخص با تاخیرهای زمانی متعدد
عنوان اصلی مقاله:
An adaptive controller for uncertain nonlinear systems with multiple time delays
شبیه سازی در محیط سیمولینک متلب انجام شده است. (متلب 2018b)
دارای ترجمه مقاله در قالب ورد است. (فقط بخش Remark1 در صفحه 5 ترجمه نشده است)
شامل ویدیو توضیحات 9 دقیقه ای در مورد شبیه سازی و اجرای سیمولینک است.
چکیده مقاله: در این مقاله یک کنترل تطبیقی مرجع مدل پیش بین (PMRAC) برای سیستمهای غیرخطی نامشخص با تاخیرهای متعدد ورودی و حالت استفاده ارائه شده است. کنترل کننده از یک پیش بین حالت، یک سیستم کمکی و قوانین تطبیقی تشکیل شده است. قوانین تطبیقی از طریق تابع لیاپانوف به گونه ای طراحی می شوند که حالت پیش بینی کننده و حالت کمکی به طور مجانبی به متغیرهای حالت سیستم همگرا می شوند، و شرط پایداری ارائه شده برقرار می گردد. ارضای این شرط پایداری وابسته به تاخیر، که در قالب یک نامعادله ماتریس خطی (LMI) فرموله شده است، پایداری سیستم کنترل حلقه بسته را تضمین می کند. مطالعات عددی با مدل استاندارد هواپیمای F-16 برای نشان دادن کارایی کنترلر پیشنهادی مورد ارائه گردیده است.
مقدمه مقاله: طراحی یک کنترلر که قادر به جبران تاخیرهای زمانی ناپایدارکننده سیستم های حلقه بسته، یک مساله بسیار چالشبرانگیز است. زمانی که سیگنالهای فیدبک از کنترلر عبور میکنند، به دلیل تاخیر در ورودیهای کنترل و/یا کانالهای فیدبک، نسبت به وضعیت سیستم از نظر زمانی عقب میمانند. در نتیجه، سیگنالهای فیدبک اثر تثبیتکنندهای که برای دستیابی به آن طراحی شدهاند را ندارند (فریدمن، 2014؛ هیل و لونل، 2013). برای غلبه بر این چالش، روش های بسیاری ارائه شده اند. به عنوان مثال، مدل پیش بین کلاسیک اسمیت (1959) برای سیستم های تاخیر پایدار ارائه شد. سپس اصلاحات زیادی بر روی آن در Astrom، Hang و Lim (1994)، Matausek و Micic (1996) و Watanabe و Ito (1981) ارائه شد که به بهبود عملکرد آن منجر گشته است. برای سیستم هایی با متغیرهای حالت انتگرالی، روش های دیگری مانند Paor (1985) و Majhi و Atherton (2000) پایداری فرآیندهای ناپایدار با تاخیر را امکان پذیر می کند. روشهای کلاسیک بعدی عبارتند از طرح Artstein، که یک سیستم با تاخیر ورودی را به یک سیستم بدون تاخیر تبدیل می کند، و یا عملگرهای Padé approxi-mants (Lam, 1993) و Hankel (Curtain & Zwart, 2012) که تاخیر را تقریب می زنند. اصطلاحات دیگری بر روی توابع انتقال ، کنترل حالت لغزشی (Roh & Oh، 1999)، و کنترل H∞ صورت گرفته است (فریدمن و شاکد، 2002).
یکی از رایج ترین روش ها برای جبران تاخیر ورودی، فیدبک خطی بر مبنای حالت پیش بینی شده است.
حالت های پیش بینی شده معمولاً به شکل یک انتگرال بر روی مقادیر گذشته ورودی کنترل قرار داده می شوند. این الگوریتمهای فیدبک پیشبینیکننده اغلب به عنوان کنترلکنندههایی با طیف محدود نامیده میشوند، که در آنها میتوان با طراحی ماتریسهای بهره فیدبک، مقادیر ویژه را در مکان های مطلوب قرار داد (Kwon & Pearson, 1980; Manitius & Olbrot, 1979 مراجعه کنید).
روشهای فیدبک پیشبینیکننده، ساختارهای پایه ای را برای نوآوریهای بعدی در جبران تاخیر فراهم میکنند. به طور خاص، پیشرفتهای مهم اخیر در کرستیک (2009، 2010)، تسوباکینو، کرستیچ، و اولیویرا (2016) و ژو، کرستیچ، و سو (2017) یک سیستم تاخیر را به یک ساختار PDE-ODE سری تبدیل میکنند که در آن از روش های کنترل شرایط مرزی برای پایداری استفاده می شوند. کنترلکنندههای مرزی به گام به عقب هم هستند که به صورت فیدبک خروجی برای سیستمهای LTI با تاخیر ورودی در Cacace و Germani (2017)، با تاخیر متغیرهای حالت و ورودی در Kharitonov (2017) و یک کنترلکننده ناظر-پیشبین در Mazenc and Malisoff (2017) ارائه گردیده اند. پژوهش ارائه شده در Bekiaris-Liberis و Krstic (2010) یک الگوریتم پیشبینی کننده فیدبک را برای جبران تاخیرهای متغیرهای حالت ناشناخته و ورودی در سیستمهای پیشخور خطی ایجاد کردند. یک روش کنترل مرزی PDE با پایداری محلی در Zhu، Krstic و Su (2018b) ارائه شده است تا اثرات تاخیرهای ورودی مجزا و ناشناخته در سیستمهای LTI را کاهش دهد. سپس این روش، در ژو، کرستیک و سو (2018) با این فرض که متغیرهای حالت برای دستیابی به پایداری قابل اندازهگیری هستند، اصلاح شد. ژو، کرستیک و سو (2019) این روش را برای سیستمهای خطی فیدبک خروجی گسترش دادند.
پژوهش اخیر لیو و ژو (2016، 2018) و ژو (2014) اصلاحاتی، به نام پیش بینی تودرتو، را برای سیستم های با متغیرهای حالت انتگرالی پیشنهاد می کند که منجر به پیش بینی متغیر حالت می شود. هدف این کار مقابله با تأخیرها در ورودی حالت و کنترل است. چندین مقاله که به سیستمهای غیرخطی میپردازند شامل طرحهای فیدبک پیشبینیکننده در Bekiaris-Liberis و Krstic (2012، 2016) و Bresch-Pietri and Krstic (2014)، Karafyllis و Krstic (2016) و نیز Karafyllis و Krstic (2016) هستند.
یکی از ویژگیهای مهم روش های پیشبینی فیدبک این است که اجرای کنترل آنها مستلزم تقریب شرایط انتگرال با مجموع محدود است. همانطور که در Engelborghs، Dambrine و Roose (2001) نشان داده شده است، این تقریب ممکن است باعث از دست دادن پایداری شود. علاوه بر این، زمانی که تعداد نقاط گسسته برای بهبود دقت زیاد باشد، پیاده سازی به زمان محاسبات طولانی نیاز دارد. به عنوان مثال، همانطور که در جدول 1 در لیو و ژو (2018) گزارش شده است، 432 ثانیه طول می کشد تا یک شبیه سازی 30 ثانیه ای با 40 نقطه گسسته انجام شود.
در این مقاله، یک کنترلر ارائه گردیده است که قادر به جبران تاخیرهای متعدد در حالتها و ورودیهای کنترل یک سیستم غیرخطی نامشخص می باشد و در عین حال عملکردهای گذرا و حالت پایدار مطلوب را حفظ میکند. سیستمهای با تاخیرهای متعدد در ورودیها و حالتهای کنترل، ساختارهای متفاوتی در مقایسه با سیستم های تک تاخیری دارند. علاوه بر این، زمانی که تاخیر ورودی بزرگتر از تاخیر حالت باشد، محاسبه پیش بینی کننده حالت به متغیرهای حالت آینده نیاز دارد، بنابراین قابل اجرا نیست (ژو، 2014).
برای پرداختن به سیستم های با تاخیرهای متعدد، از چارچوب PMRAC در لاورتسکی، گادینت و گریگوری (2010)، نگوین (2018)، نگوین و دانکوویچ (2019) و نگوین، لی و دانکوویچ (2018) استفاده میکنیم. طرح پیشنهادی در این مقاله از چهار جزء کلیدی تشکیل شده است: سیستم کمکی، پیشبینیکننده حالت، قوانین تطبیقی، و ورودی کنترل. سیستم کمکی و پیش بینی کننده حالت به گونه ای ساخته شده اند که انحرافات بین هر یک از این سیستم ها و وضعیت سیستم مستقل از تاخیرهای ورودی باشد. سپس قوانین تطبیقی به گونهای طراحی میشوند که یک تابع لیاپانوف منفی شود، و از این رو، انحرافات به صورت مجانبی به صفر همگرا میشوند. این ساختار جبران تاخیر چندین مزیت را به همراه دارد. این روش می تواند سیستم های غیرخطی نامشخص را با تاخیرهای زمانی ورودی و حالت های متعدد پایدار کند. هر جزء آن به راحتی قابل پیاده سازی است. از این رو، هیچ نگرانی در مورد گسسته سازی و پیاده سازی یکپارچه مرتبط با کنترل کننده های فیدبک پیش بینی وجود ندارد. علاوه بر این، از آنجایی که از ساختار کلاسیک MRAC استفاده می کند، موانع بسیار کمی برای اجرا دارد. هر مهندس کنترلی که با MRAC آشناست باید بتواند طرحهای جبران تاخیر را برای کارهای خاص اجرا کند. طرح پیشنهادی همچنین توانایی دستیابی به عملکرد عالی ردیابی گذرا را از MRAC اصلی به ارث برده است.
فرض های در نظر گرفته شده در این مقاله عبارتند از: (i) فرض میکند که ضرایب ورودیهای کنترل مشخص هستند. (ii) یک حد بالایی برای تاخیرهای ورودی وجود دارد که فراتر از آن سیستم کنترل حلقه بسته بیثبات میشود.
توضیحات پروژه کنترلر تطبیقی سیستم های غیرخطی نامشخص
در این پروژه مدل و روش اصلی مقاله در سیمولینک متلب پیاده سازی شده است, به همراه گزارش ویدیوی و ترجمه مقاله در قالب ورد.
در ویدیو بخوبی شبیه سازی تشریح شده است.
نتایج بدست آمده از شبیه سازی با متلب:
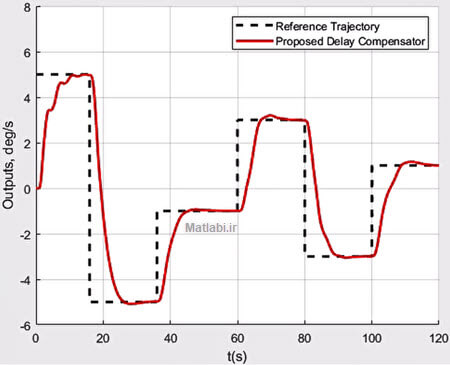
Fig. 1. Tracking performance of the proposed delay compensator as compared with the controller in Nguyen (2018). In this case, the input and state delays are τ = 0.2 s and h = 2 s, respectively.
شکل 1. عملکرد ردیابی جبران کننده تاخیر پیشنهادی در مقایسه با کنترل کننده در Nguyen (2018). در این حالت تاخیرهای ورودی و حالت به ترتیب ث0.2=تاو و اچ = 2ث هستند.
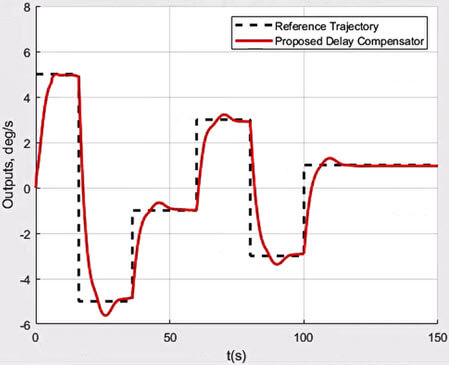
Fig. 2. Tracking performance of the proposed delay compensator. In this case, the input and state delays are τ1 = 0.5 s, τ2 = 0.2 s, and h = 5 s, respectively, for the system controlled by the controller proposed in this paper
شکل 2. عملکرد ردیابی جبران کننده تاخیر پیشنهادی. در این مورد، تاخیرهای ورودی و حالت به ترتیب τ1 = 0.5 ثانیه، τ2 = 0.2 ثانیه و h = 5 ثانیه برای سیستم کنترل شده توسط کنترل کننده پیشنهادی در این مقاله است.
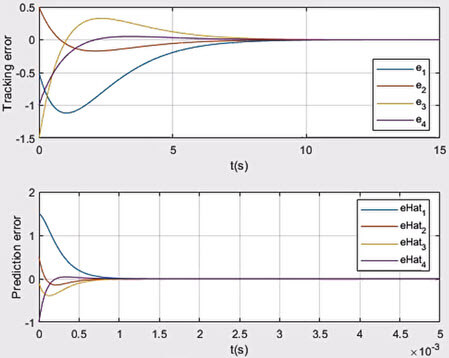
Fig. 3. The top panel shows the time histories of the tracking error e(t) = x(t) − xa(t). The bottom panel shows the time histories of the prediction error eˆ(t) = xˆ(t)−x(t). In this case, the input and state delays are τ1 = 0.5 s, τ2 = 0.2 s, and h = 5 s, respectively, and the control system is tasked to track a step input. Asymptotic stability is evident in both tracking and prediction errors despite the large delay values
شکل 3. پانل بالایی تاریخچه زمانی خطای ردیابی e(t) = x(t) – xa(t) را نشان می دهد. پانل پایینی تاریخچه زمانی خطای پیش بینی eˆ(t) = xˆ(t)−x(t) را نشان می دهد. در این حالت، تاخیرهای ورودی و حالت به ترتیب τ1 = 0.5 ثانیه، τ2 = 0.2 ثانیه و h = 5 ثانیه است و سیستم کنترل وظیفه دارد یک ورودی مرحله ای را ردیابی کند. پایداری مجانبی در هر دو خطای ردیابی و پیشبینی با وجود مقادیر تاخیر زیاد مشهود است.

Fig. 4. Tracking performance of the proposed delay compensator. In this case, the input and state delays are τ1 = 5.7 s, τ2 = 0.2 s, and h = 5 s, respectively.
شکل 4. عملکرد ردیابی جبران کننده تاخیر پیشنهادی. در این حالت، تاخیرهای ورودی و حالت به ترتیب τ1 = 5.7 ثانیه، τ2 = 0.2 ثانیه و h = 5 ثانیه است.
ترجمه نتیجه گیری مقاله:
در این مقاله یک کنترلر جبران تاخیر تطبیقی جدید با استفاده از PMRAC ارائه شده است. رویکرد پیشنهادی قادر است سیستمهای غیرخطی نامشخص را با تاخیرهای متعدد در ورودیها و حالتهای کنترل پایدار کند. یک شرط پایداری وابسته به تاخیر با استفاده از تابع لیاپانوف-کراسوفسکی ارائه شده است. هنگامی که مقادیر تاخیر کمتر از آستانه بالا هستند، پایداری مجانبی سیگنال های خطا و پایداری ورودی به حالت سیستم کنترل تطبیقی حلقه بسته تضمین می شود. علاوه بر این، بر خلاف بسیاری از دیگر کنترلکنندههای جبران تاخیر، طرح پیشنهادی نیازی به گسستهسازی ندارد.
بنابراین، از نظر محاسباتی کارآمدتر از کنترلکنندههای فیدبک پیشبینیکننده است، که قوانین کنترل آنها بر حسب انتگرالها فرمولبندی میشوند و از موضوع زمان پردازش طولانی رنج میبرند، که به عنوان مثال در لیو و ژو (2018) گزارش شده است. همچنین نتایج مقایسهای نشان دهنده عملکرد طرح پیشنهادی با توجه به کنترلکنندههای جبران تاخیر موجود است.
شاید به موارد زیر نیز علاقه مند باشید:
- تشخیص و جداسازی عیب حسگر برای یک کلاس از سیستم غیرخطی نامشخص با استفاده از رویتگر مود لغزشی
- طراحی ناظر تابعی با مرتبه کسری ورودی نامشخص برای سیستم های مرتبه کسری با تاخیر زمانی لیپشیتس یک طرفه
- سفارش شبیه سازی مقالات کنترل غیرخطی با متلب
- کنترل سرعت موتور DC به همراه دست یابی به زمان نشست کوتاه در پاسخ سیستم
- تشخیص عیب برای سیستم های LPV گسسته با استفاده از مشاهده کننده فاصله زمانی
کلیدواژه:
Delay compensation, Adaptive control, Nonlinear systems
جبران تاخیر, کنترل تطبیقی, سیستم های غیرخطی
کنترل کننده تطبیقی برای سیستم های غیرخطی نامشخص با تاخیرهای زمانی متعدد با متلب
طبق توضیحات فوق توسط کارشناسان سایت متلبی تهیه شده است و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.





دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.