توضیحات
تنظیم بهینه کنترل کننده PID بر روی سیستم چند متغیره خلبان خودکار طولی هواپیما براساس الگوریتم اجتماع ذرات (PSO)
در این مقاله طراحی کنترل کننده بهینه حول محور طولی در یکی از شرایط پروازی سیستم چندمتغیره هواپیما برای کنترل مجزای زاویه حمله از زاویه وضعیت پیچش (که در مدهای اعمال نیروی مستقیم حول محورطولی مورد استفاده میگیرد) با استفاده از الگوریتم بهینه سازی اجتماع ذرات (PSO) ارائه میشود.
همان طور که میدانیم طراحی کنترل کننده حول محور طولی و حول محور سمتی- جانبی منجر به طراحی سیستم خلبان خودکار در هواپیما خواهد شد.
سیستم خلبان خودکار در اکثر سازههای هوایی امروزی به یک جزء اساسی و جداییناپذیر تبدیل شده است.
به نحوی که کمترهواپیمای نظامی و یا غیرنظامی را می توان یافت که از این سامانه بیبهره مانده باشد.
از طرف دیگر به دلیل مشکلاتی نظیر معادلات حرکتی غیرخطی و پیچیده حاکم بر رفتار دینامیکی این گونه سازهها، طراحی سیستم خلبان خودکار به راحتی امکانپذیر نمیباشد.
ارائه این روش میتواند پیچیدگیهای طراحی سیستم خلبان خودکار را کاهش دهد.
این روش بر روی هواپیمای جنگنده HIMAT شبیه سازی شده است و نتایج بیانگر کارایی آن میباشد.
گزارش شبیه سازی مقاله
مسئله موردنظر: سیستم دو ورودی – دو خروچی با ماتریس های فضای حالت به فرم زیر:
گام اول، شبیه سازی open loop
دو راه جهت شبیه سازی سیستم فوق وجود دارد، راه اول استفاده از سیمولینک و راه دوم استفاده از m-file می باشد، با توجه به اینکه در ادامه عملیات بهینه سازی در راستای یافتن یک کنترلر بهینه بر روی سیستم موردنظر احتیاج است، لذا استفاده از m-file به جهت کاهش مدت زمان run سیستم پیشنهاد می شود:
بنابراین با نوشتن کد زیر در محیط matlab خواهیم داشت:
|
clc close all clear all %============================================================= A=[0.023 -37 -19 -32;0 -1.9 0.98 0.01;0.012 -12 -26 0;0 0 1 0]; B=[0 0;-0.41 0;-78 22;0 0]; … |
خروجی:
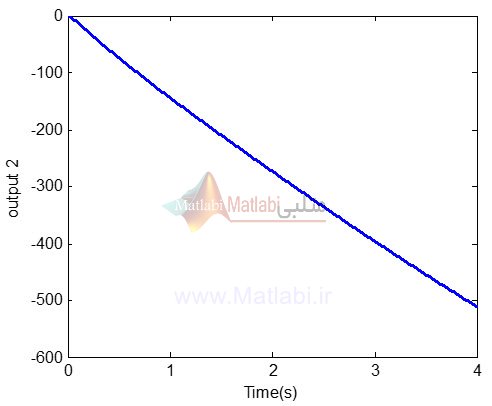
بنابراین خروجی سیستم در حالت ورودی step برای input 1 برای دو خروجی سیستم به صورت زیر می باشد:
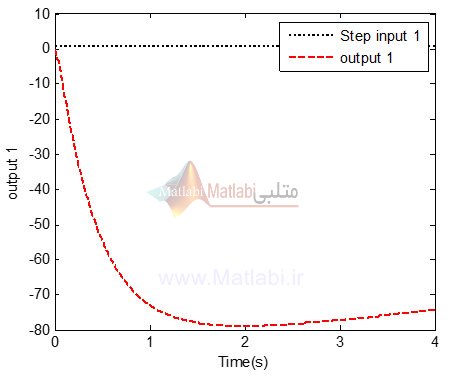
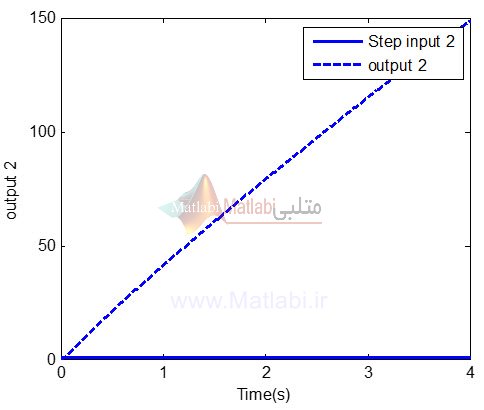
هم چنین، با اجرای کد فوق، نتایج برای خروجی سیستم در حالت ورودی step برای input 2 برای دو خروجی سیستم به صورت زیر می باشد:
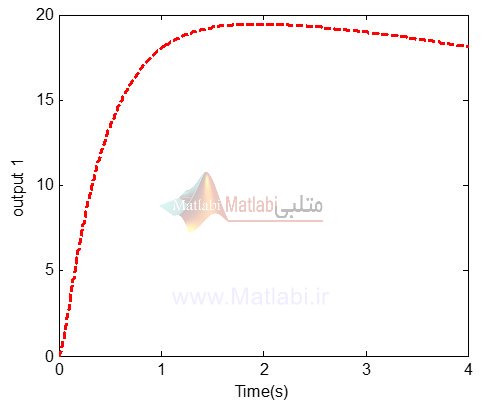
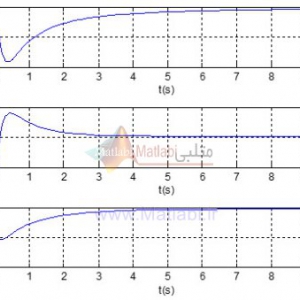
همانطور که از نتایج فوق مشهود است سیستم ناپایدار بوده و بنابراین می بایست جهت پایدارسازی آن از یک کنترل کننده استفاده نمود.
در این مقاله از کنترل کننده PID جهت پایدارسازی استفاده شده است که بهره های بهینه این کنترل کننده توسط الگوریتم های ژنتیک و PSO یافته و مورد استفاده قرار گرفته است:
معیار مورد استفاده در بهینه سازی پارامترهای کنترلی PID به صورت زیر می باشد:
که در آن ، ()، حداکثر فراجهش و تفاضل مقدار خروجی شماره i ام از ورودی مرجع شماره jام و W ضریب وزنی اهداف و نیز به عنوان تابع معیار یا تابع هدف تعریف می گردد.
علاوه براین ساختار کنترل کننده چند متغیره به صورت زیر تعریف می گردد:
محدوده تغییرات پارامترهای کنترل کننده نیز به صورت زیر تعریف شده است:
لازم به ذکر است که از یک پیش فیلتر در مسیر ورودی های مرجع به صورت زیر ا ستفاده شده است:
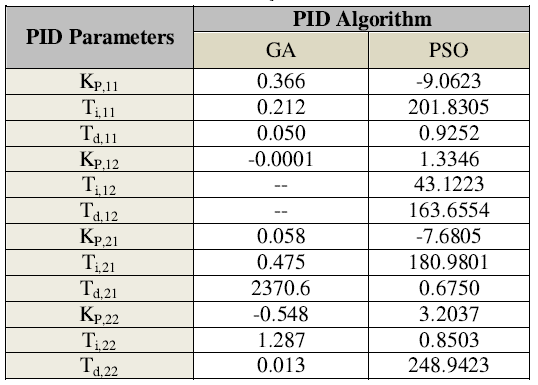
نتایج ارائه شده توسط مقاله، برای کنترل کننده های PSO و GA در جدول زیر داده شده است:
کنترل کننده طراحی شده براساس روش شکل دهی حلقه به فرم زیر می باشد:
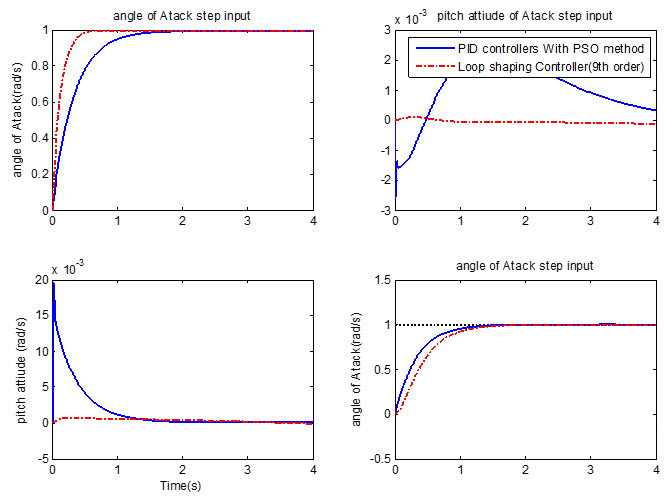
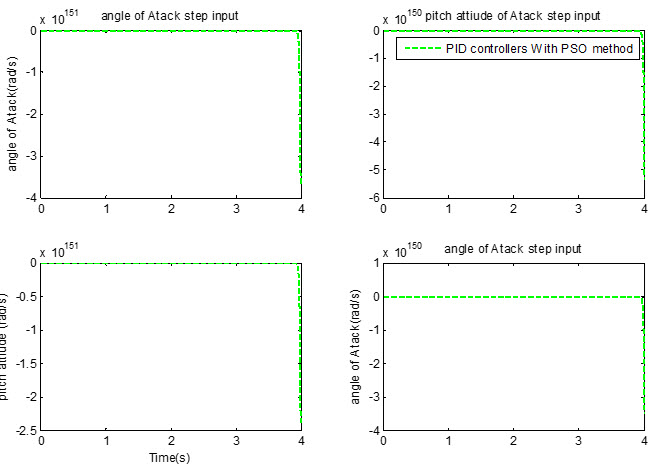
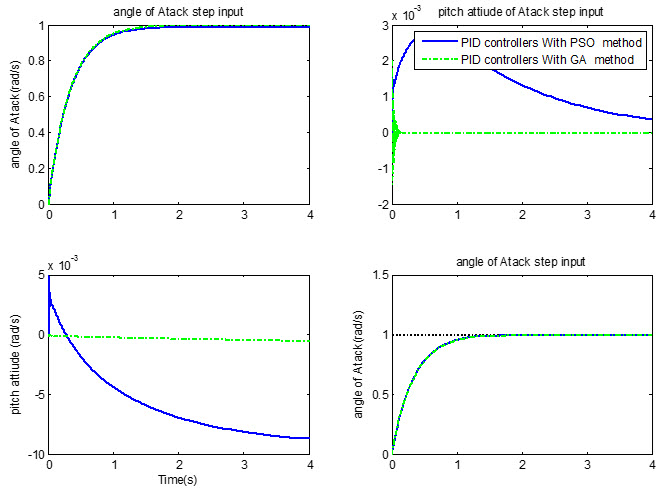
نتایج ارائه شده از بهره های پایدارکننده با استفاده از الگوریتم ژنتیک در پایدارسازی سیستم، به اشتباه در مقاله ارائه شده، چرا که این نتایج نمی تواند سیستم را پایدار کند، ابتدا نتایج حاصل از کنترل کننده های PSO و روش شکل دهی حلقه ارائه می شود و در نهایت نتایج ناپایداری ناشی از بهره های بهینه شده با استفاده از الگوریتم ژنتیک ارائه می شود (این بهره ها به اشتباه در مقاله ارائه شده است).
نتایج حاصل از اعمال کنترل کننده PSO و روش شکل دهی حلقه
|
clc close all clear all %======================================================================================= %=============================================== A=[0.023 -37 -19 -32;0 -1.9 0.98 0.01;0.012 -12 -26 0;0 0 1 0]; B=[0 0;-0.41 0;-78 22;0 0]; C=[0 57 0 0;0 0 0 57]; … |
خروجی:
نتایج ارائه شده در فوق با نتایج مقاله یکسان می باشد.
به منظور اثبات غلط بودن نتایج مربوط به بهینه سازی با استفاده از الگوریتم ژنتیک ارائه شده در مقاله، کد زیر به بررسی پاسخ سیستم پس از اعمال کنترل کننده می پردازد:
|
clc close all clear all %======================================================================================= %=============================================== A=[0.023 -37 -19 -32;0 -1.9 0.98 0.01;0.012 -12 -26 0;0 0 1 0]; B=[0 0;-0.41 0;-78 22;0 0]; C=[0 57 0 0;0 0 0 57]; … |
نتایج:
می بینیم که سیستم به شدت ناپایدار شده است.
بنابراین نتایج ارائه شده مربوط به بهره های بهینه با استفاده از الگوریتم ژنتیک اشتباه می باشد.
به منظور پایدار سازی سیستم با استفاده از الگوریتم PSO و Genetic، در ادامه به یافتن بهره های بهینه با استفاده از این دو الگوریتم پرداخته می شود.
گام ابتدایی در یافتن پارامترهای بهینه، ایجاد تابع هدف، براساس معیارات ذکر شده در مقاله می باشد، بدین منظور cost_function زیر با گرفتن، 12 پارامتر، متشکل از 4 عدد بهره Kp، 4 عدد بهره Ti و 4 عدد بهره Td، رفتار سیستم را براساس تابع هدف تعریف شده مورد بررسی قرار می دهد و cost مورد نظر را مورد محاسبه قرار می دهد:
|
% clc % close all % clear all function cost=cost_function(para) %=============================================== A=[0.023 -37 -19 -32;0 -1.9 0.98 0.01;0.012 -12 -26 0;0 0 1 0]; B=[0 0;-0.41 0;-78 22;0 0]; C=[0 57 0 0;0 0 0 57]; … |
کد الگوریتم ژنتیک زیر به منظور یافتن بهره های بهینه کنترلی مورد استفاده قرار گرفته است، در واقع الگوریتم زیر با استفاده از تابع هدف تعریف شده در فوق، به سمت بهینه ترین جواب حرکت می کند:
|
clc close all clear %========================================================================== % define the requirement variables || %========================================================================== %define the zone of answer X_max=[10*ones(1,4) 1e+3*ones(1,4) 1e+3*ones(1,4)]; % … |
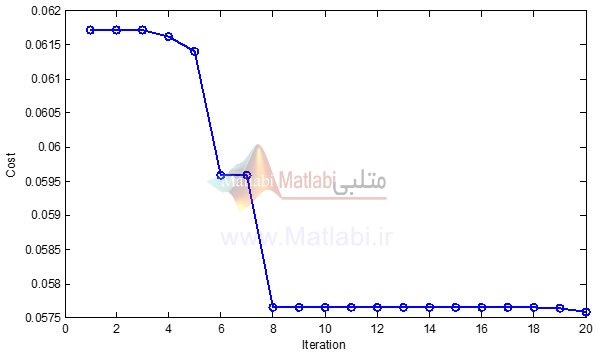
می نیمم شدن تابع هزینه با استفاده از الگوریتم ژنتیک در زیر ارائه شده است:
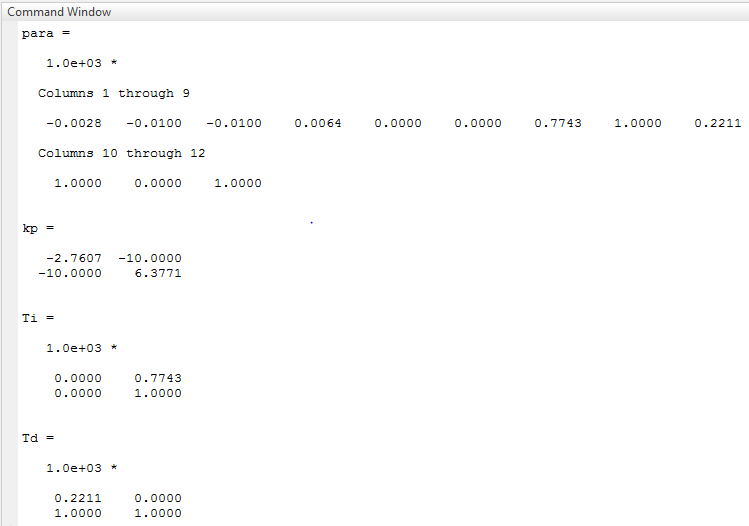
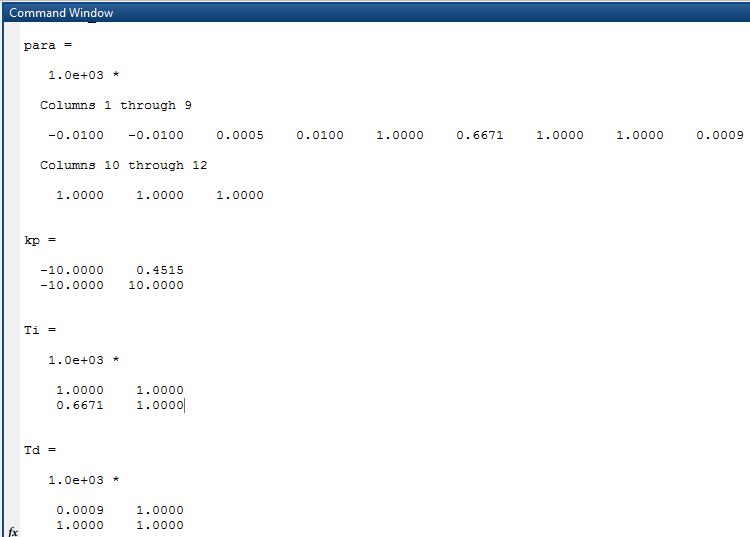
پارامترهای بهینه بدست آمده در زیر ارائه شده است:
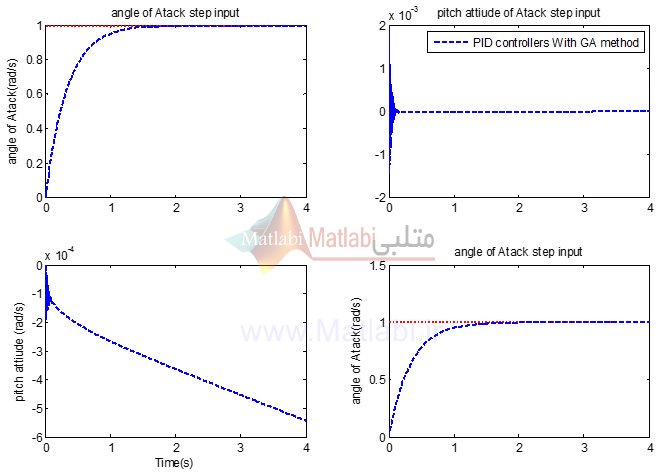
با اعمال پارامترهای بهینه بدست آمده رفتار سیستم مورد بررسی قرار گرفته است:
در راستای بهینه شدن پارامترهای کنترلی از الگوریتم PSO مندرج در زیر به منظور بهینه سازی پارامترهای کنترلی استفاده شده است:
|
clc;clear close all N=input(‘enter number of initial population :’); X_max=[10*ones(1,4) 1e+3*ones(1,4) 1e+3*ones(1,4)]; % … |
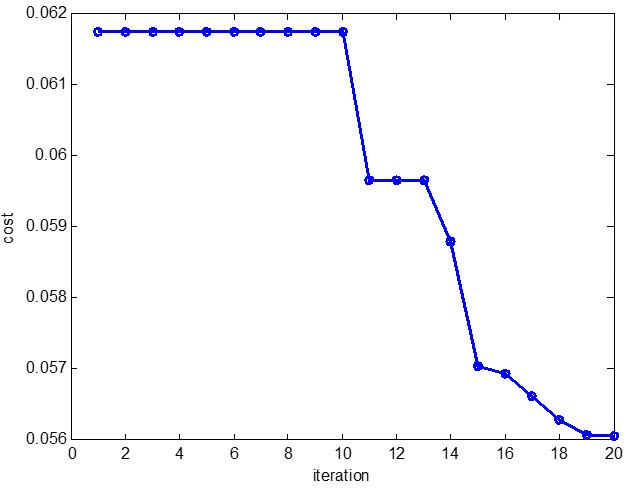
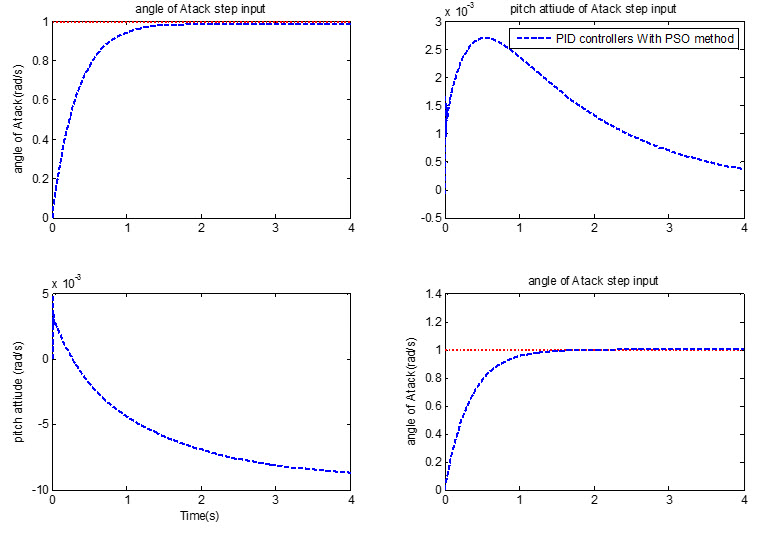
می نیمم شدن تابع هدف با استفاده از الگوریتم PSO نوشته شده در زیر ارائه شده است:
پارامترهای بهینه یافته شده با استفاده از الگوریتم ژنتیک در زیر داده شده است:
با اعمال نتایج بدست آمده از الگوریتم PSO نتیجه به صورت زیر خواهد بود:
پارامترهای بهینه شده با استفاده از الگوریتمهای ژنتیک و PSO به پیوست در دو فایل mat ذخیره شده است.
کد زیر به مقایسه عملکرد پارامترهای کنترلی بدست آمده با استفاده از دو الگوریتم GA و PSO می پردازد:
|
clc close all clear all %=================================== load GAanswer para A=[0.023 -37 -19 -32;0 -1.9 0.98 0.01;0.012 -12 -26 0;0 0 1 0]; B=[0 0;-0.41 0;-78 22;0 0]; … |
نتیجه بعد از Run:
کلید واژه : سیستمهای چندمتغیره؛ الگوریتم بهینه سازی اجتماع ذرات (Particle Swarm Optimization)؛ خلبان خودکار طولی؛ معادلات حرکت هواپیما, پروژه متلب, پروژه matlab , شبیه سازی با متلب
Swarm intelligence, particle swarm optimization algorithms, PID controllers, MIMO systems, longitudinal autopilot, aircraft equation of motion
شبیه سازی
تنظیم بهینه کنترل کننده PID بر روی سیستم چند متغیره خلبان خودکار طولی هواپیما براساس الگوریتم اجتماع ذرات (PSO)
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

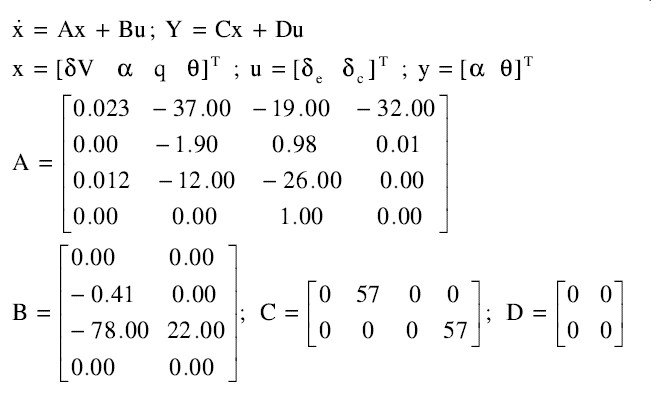

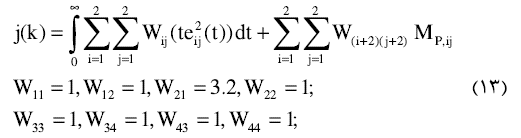

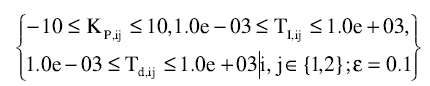
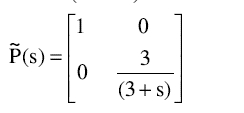



دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.