توضیحات
تحقق کانونیکال برای سیستم پیوسته در سیمولینک متلب
انجام 4 سوال زیر:
- یک تحقق کانونیکال برای سیستم پیوسته خود بنویسید.
- روش شناسایی فضای حالت را با فرض در دسترس بودن متغیرها، بر روی این سیستم پیاده کنید.
- فرض کنید متغیرهای حالت در دسترس نبوده و تنها خروجی سیستم را داریم. یک رویتگر تطبیقی برای سیستم طراحی کنید.
- اثر غنی بودن ( PE ) سیگنال ورودی را بر روی شناسایی بررسی کنید.
دارای فایل های شبیه سازی و گزارش مختصر
در زیر گزارش این شبیه سازی آمده است:
هر جا … قرار داده شده, با خرید محصول دسترسی به آن قسمت خواهید داشت و قابل مشاهده خواهد بود.
قسمت اول سوال
تحقق کانونیکال را به صورت زیر مینویسیم.
…
این تحقق در سیمولینک به صورت زیر میباشد
…
شکل1 – تحقق مینیمال در سیمولینک
حل سوال دوم: 2روش شناسایی فضای حالت را با فرض در دسترس بودن متغیرها، بر روی این سیستم پیاده کنید.
با در نظر گرفتن مدل مرجع و شبیه سازی در محیط سیمولینک ، با فرض ورودی پله، ورودی سینوسی، و جمع سه ورودی سینوسی تابع خطای حالت و خطای حاصل از تخمین متغیر ها رسم شده است.
ورودی پله
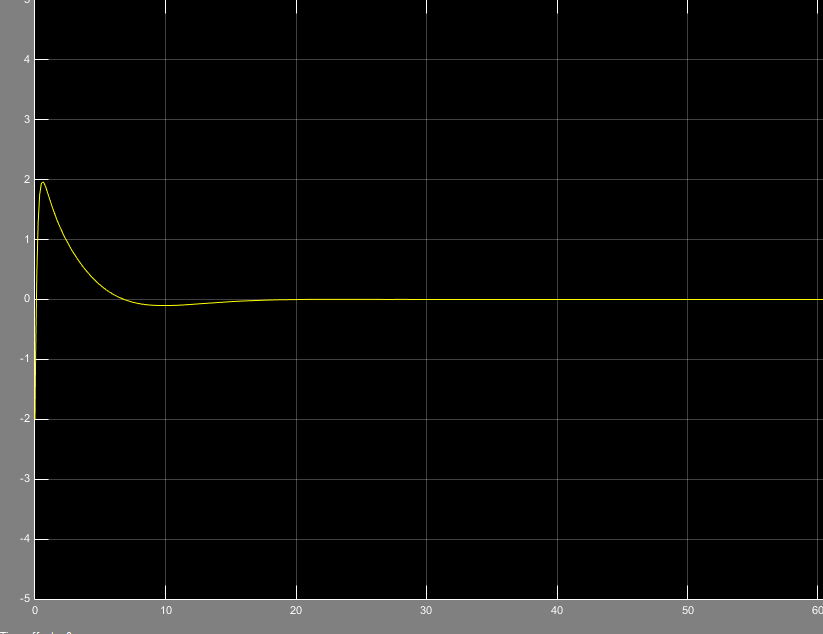
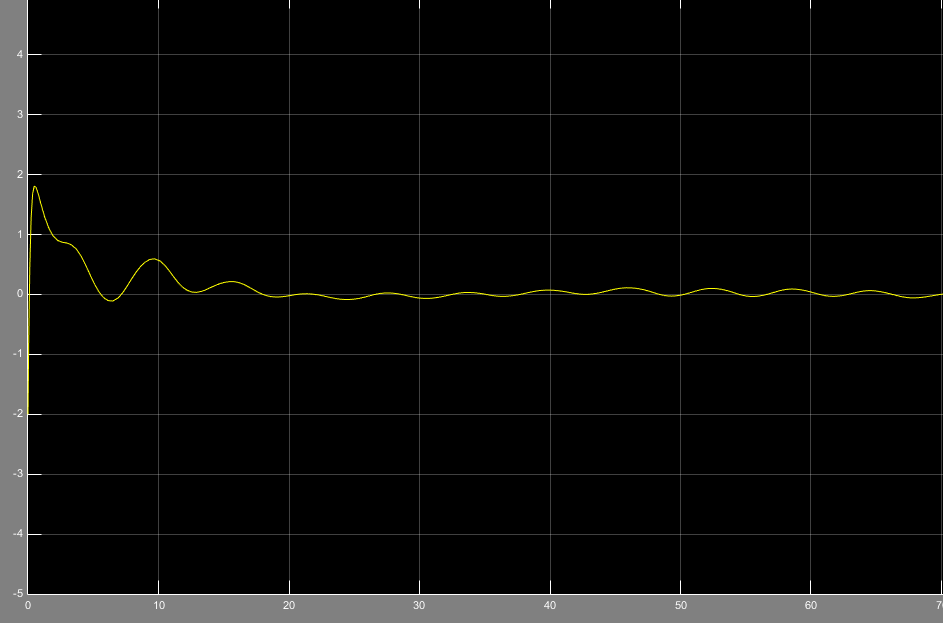
شکل2 خطای ناشی از تخمین متغیرهای حالت را نشان میدهد در این حالت ورودی را پله در نظر گرفتیم.
میبینم که خطای e در نهایت صفر میشود.
شکل2- خطای ناشی از شناسایی متغیر حالت و متغیر تخمین زده شده با ورودی پله(e)
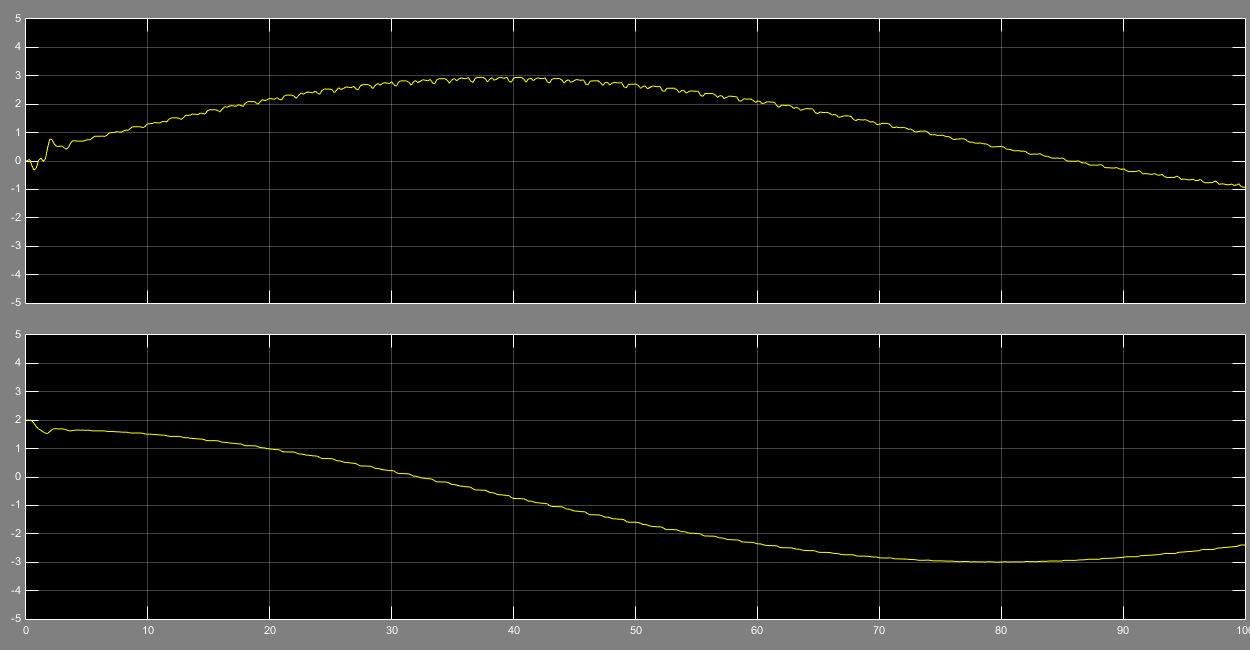
شکل شماره 3 و4 خطای پارامتر a11 و a21را با ورودی پله نشان میدهد.
همانطور که مشاهده میکنیم این خطا اگرچه پایدار است ولی به سمت صفر میل نکرده است که علت آن وجود تابع پله برای ورودی میباشد
شکل3- خطای پارامتر (a11)باورودی پله
شکل4- خطای پارامتر (a21)باورودی پله
به همین ترتیب خطای پارامتر b در محیط سیمولینک نوشته شده است.
که خطای تخمین این پارامتر هم پایدار است ولی به سمت صفر میل نمیکند.
بررسی خطای شناسایی با فرض ورودی سینوسی
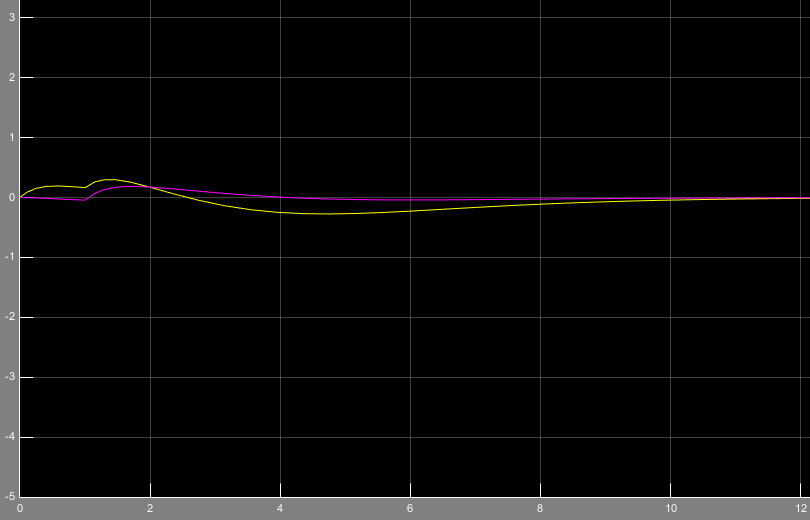
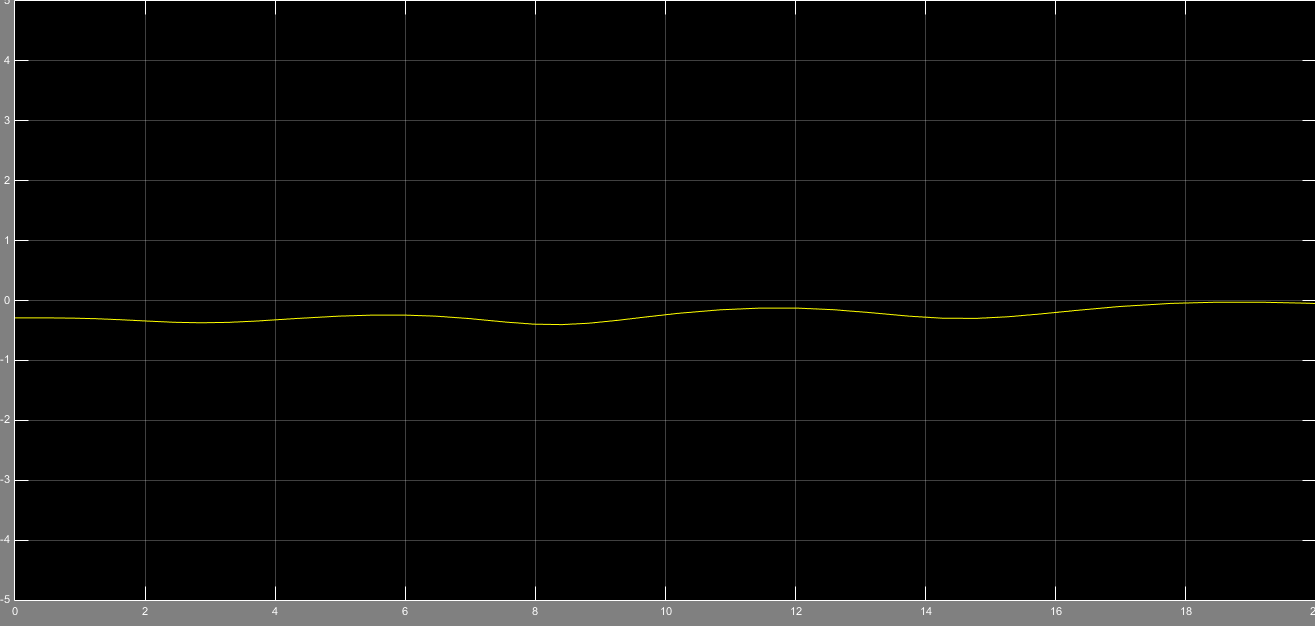
شکل شماره 5 خطای ناشی از تخمین متغیرهای حالت را با فرض ورودی سینوسی نشان میدهد که اطراف صفر نوسان میکند و در نهایت به صفر همگرا میشود.
شکل شماره 6 و7 خطای ناشی از تخمین پارامتر a11و a21 را نشان میدهد که این خطاها اگرچه پایدارند ولی همگرا به صفر نیستند.
شکل5- خطای ناشی از شناسایی متغیر حالت و متغیر تخمین زده شده با ورودی پله(e)
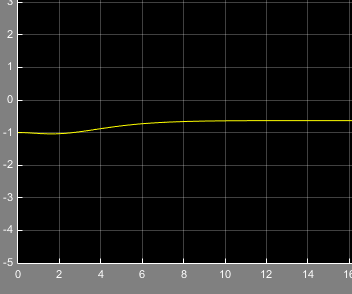
شکل6- خطای ناشی از تخمین پارامتر a11 با ورودی سینوسی
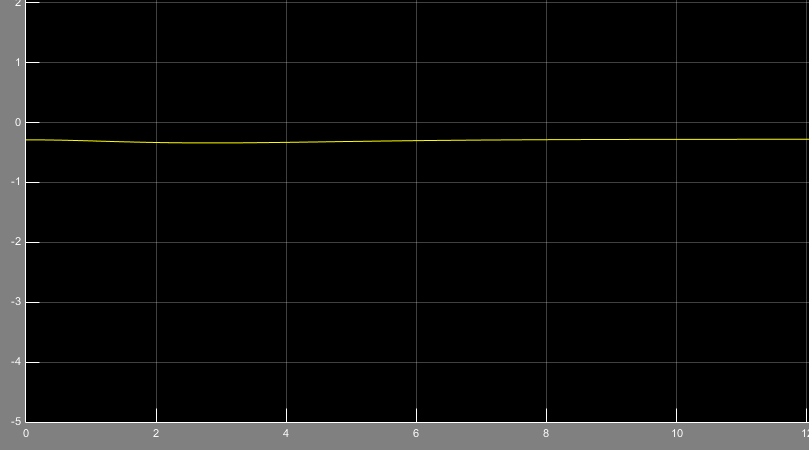
شکل7- خطای ناشی از تخمین پارامتر a21 با ورودی سینوسی
ورودی جمع سه تابع سینوسی
تخمین دوباره پارامترها با ورودی سه تابع سینوسی با فرکانسهای 1، 0.2 و 0.5 (رادیان/ثانیه) آغاز میکنیم.
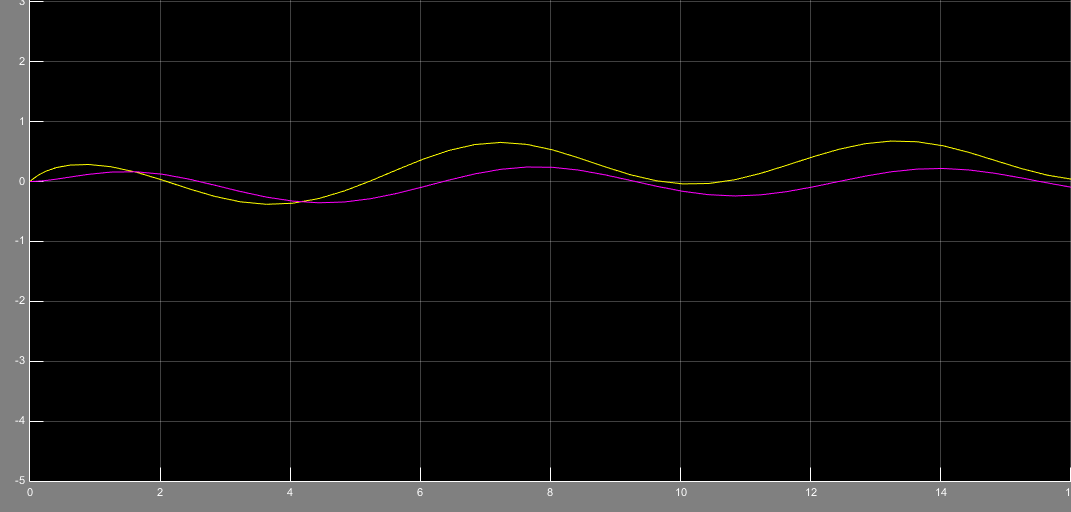
شکل 8 خطای e را نشان میدهدکه همگرا به صفر میباشد.
شکل 9 خطای ناشی از تخمین پارامتر a11 را نشان میدهد که همگرا به صفر است و شکل 10 خطای ناشی از تخمین پارامتر a21 را نشان میدهد که این خطا نیز همگرا به صفر میباشد
شکل8- خطای e با ورودی سه تابع سینوسی
شکل9- خطای ناشی از تخمین پارامتر a11 با ورودی سه تابع سینوسی
شکل10- خطای ناشی از تخمین پارامتر a21 با ورودی سه تابع سینوسی
حل سوال سوم: فرض کنید متغیرهای حالت در دسترس نبوده و تنها خروجی سیستم را داریم.
یک رویتگر تطبیقی برای سیستم طراحی کنید
برای طراحی رویتگر به صورت زیر عمل میکنیم.
K را چنان تعیین میکنیم که ماتریس … پایدار مجانبی باشد سپس با نوشتن قانون تطبیق به شکل زیر به تخمین حالت میپردازیم.
در این روابط g=k+a میباشد.
که a بردار حالت سیستم در تحقق مینیمال و b نیزبردار ضریب ورودی در حالت مینیمال میباشد.
روابط به صورت زیر شبیه سازی شده است.
برای طراحی رویتگر مینیمال از روابط صفحه 164 و 165 کتاب Narendra- stable adaptive systems استفاده شده است.
…
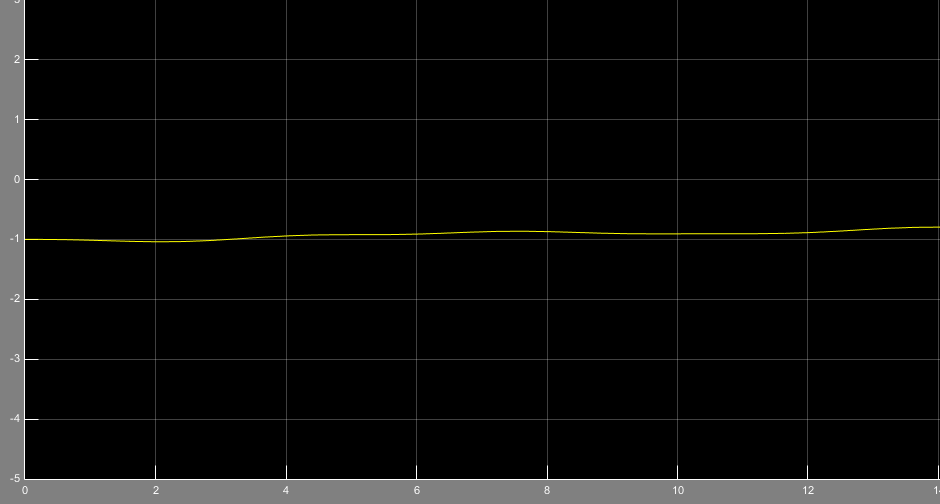
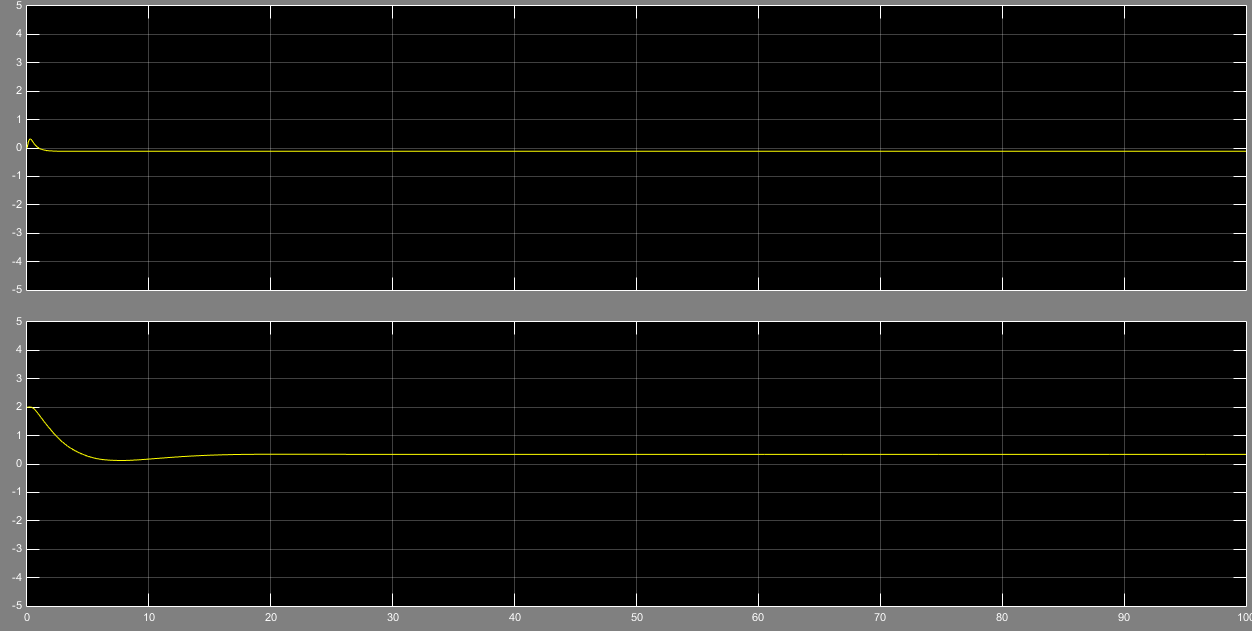
با وجود ورودی پله ، خطای ناشی از تخمین متغیر حالتx1 به صورت شکل11 میباشد که خطا به سمت صفر همگرا میشود.
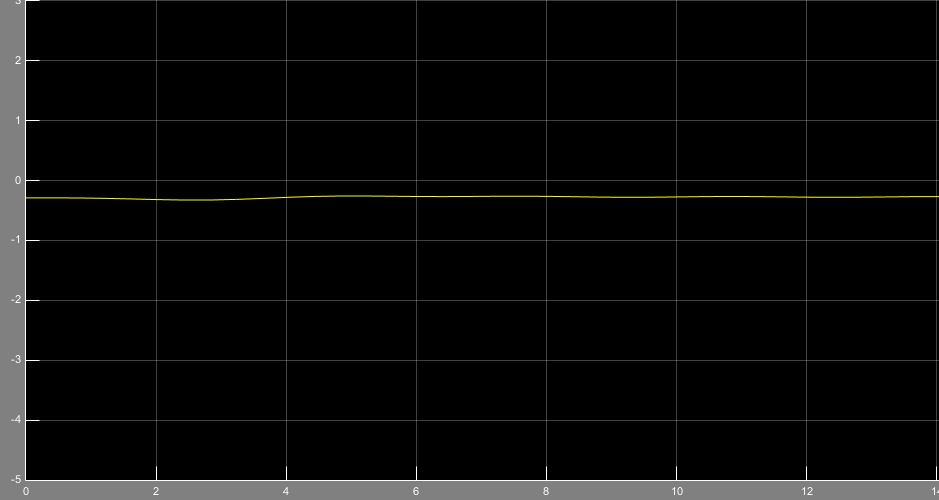
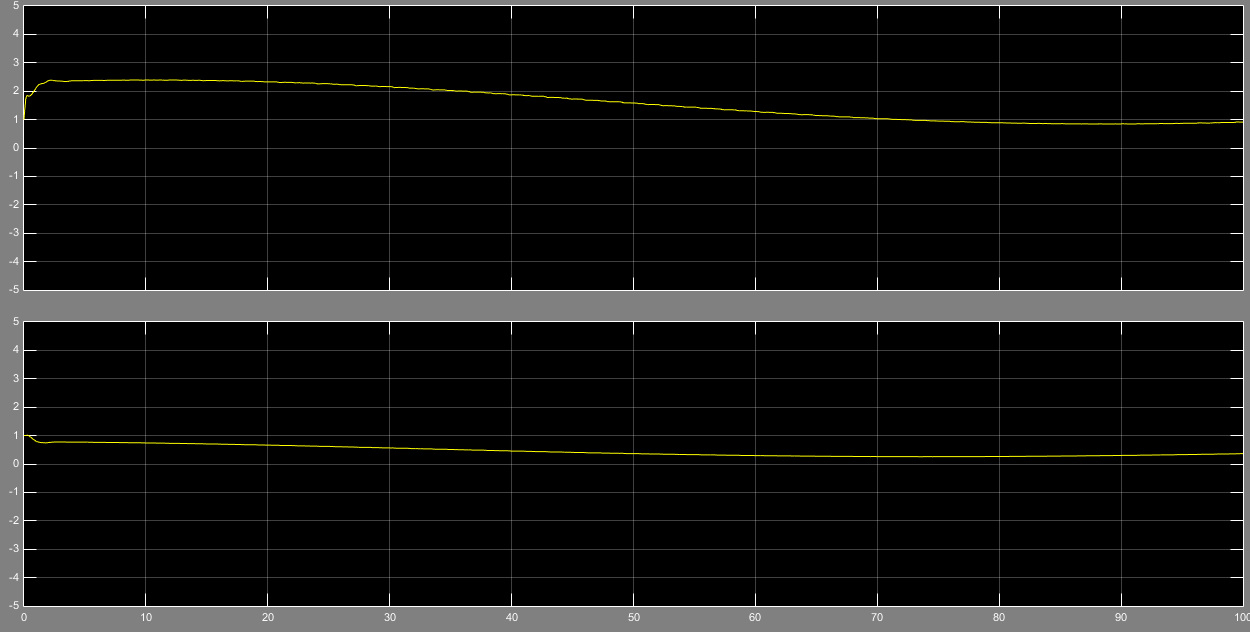
ماتریس b و g به صورت شکل 12 و 13 تخمین زده میشوند. که خطای پارامترها صفر نمیشود.
شکل 11- خطای ناشی از تخمین متغیر حالت با رویتگر تطبیقی
شکل 12- تخمین ماتریس b با رویتگر مینیمال و ورودی پله
شکل 13- تخمین ماتریس g با رویتگر مینیمال و ورودی پله
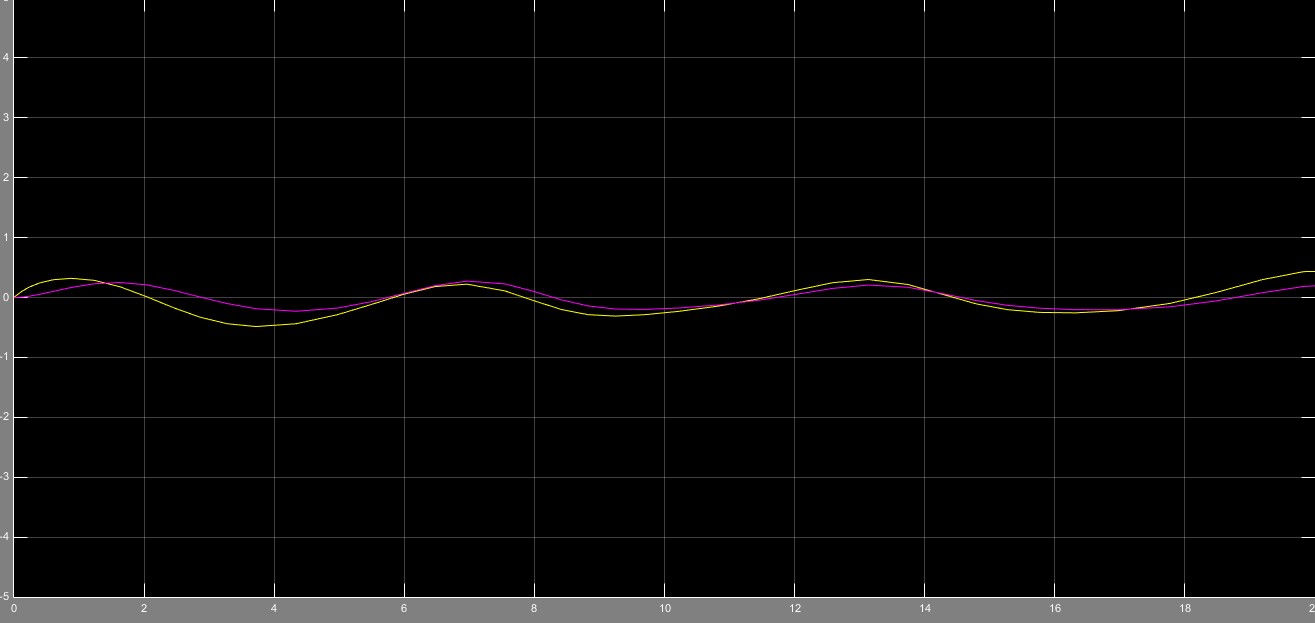
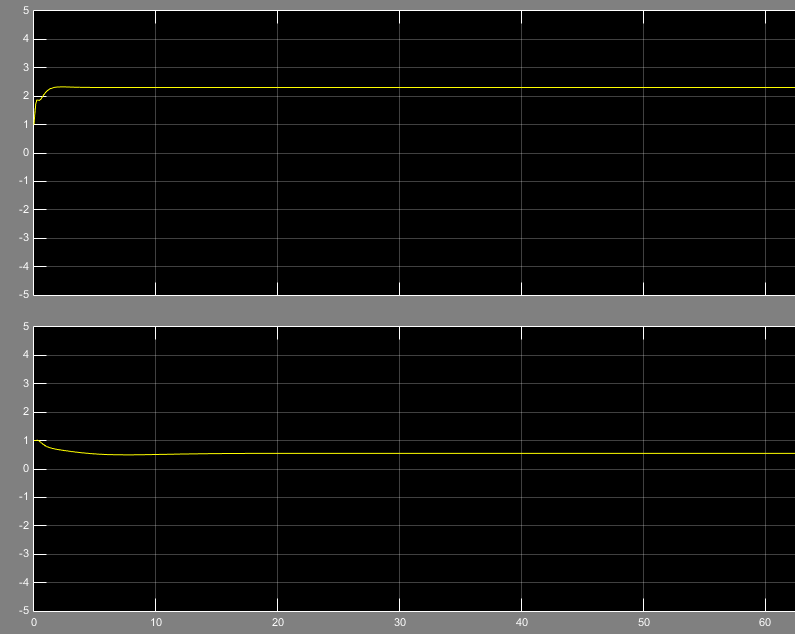
حال حالتی را بررسی میکنیم که ورودی جمع دو تابع سینوسی با فرکانس 3 و 7 (رادیان/ثانیه) باشد.
در این صورت خطای e و تخمین بردار g وb به صورت زیر میباشد.
شکل14- خطای ناشی از تخمین متغیر حالت با استفاده از رویتگر مینیمال
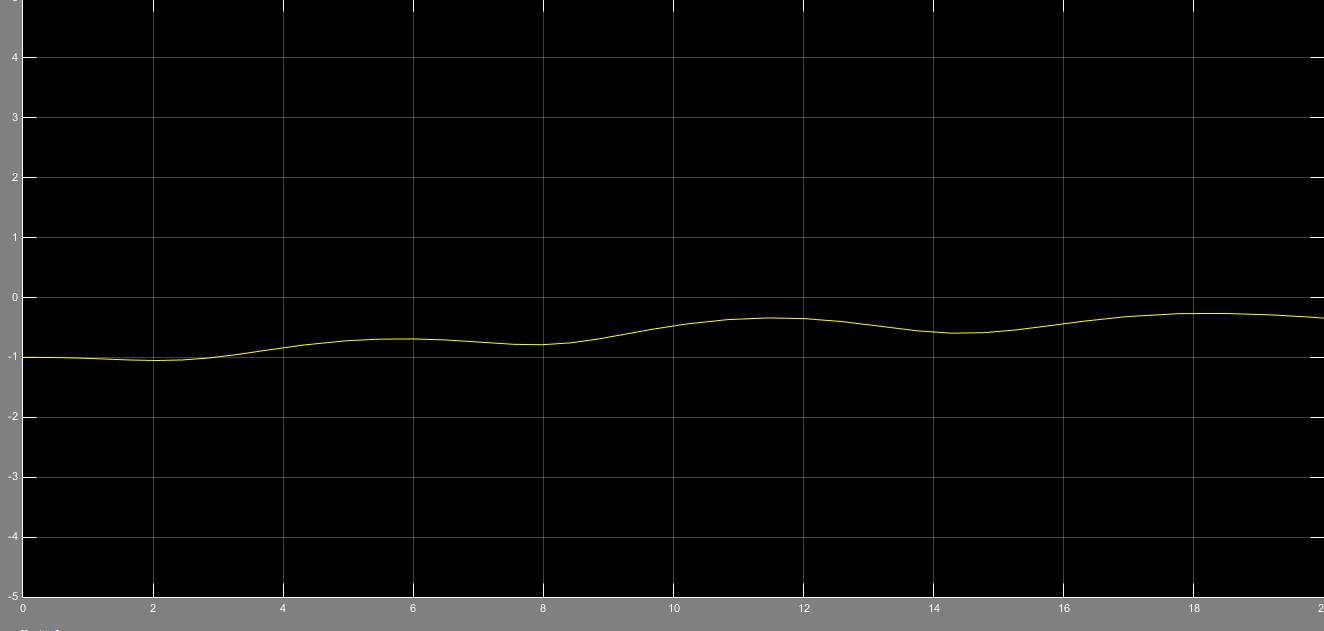
شکل 15- تخمین ماتریس b با رویتگر مینیمال و ورودی پله
شکل 16- تخمین ماتریس b با رویتگر مینیمال و ورودی پله
سوال 4ام: اثر غنی بودن سیگنال ورودی بر روی شناسایی:
در حل قسمت دوم سوال دیدیم که با ورودی پله خطای ناشی از تخمین متغیر حالت در نهایت صفر شد ولی خطای ناشی از تخمین بردارهای a و b به سمت صفر میل نکرد.
با تغییر ورودی به جمع سه تابع سینوسی با فرکانسهای مختلف مشاهده کردیم که خطای ناشی از تخمین بردار a و b به سمت صفر میرود. در بحث شناسایی قوانین تطبیق برای بردار b به صورت زیر میباشند.
همانطور که میبینیم قانون تطبیق به ورودی بستگی دارد.
و با وجود ورودیهای که فرکانس آنها شرط کافی برای تحریک مدها را داشته باشد.
کلید واژه:
تحقق کانونیکال , فضای حالت , رویتگر تطبیقی , Canonical realization
شبیه سازی
تحقق کانونیکال برای سیستم پیوسته در سیمولینک متلب
توسط کارشناسان سایت متلبی پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.





دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.