توضیحات
استفاده از ضريب انتشار تطبيقی براي حذف نويز تصاوير با استفاده از معادلات مشتقات جزيی
در اين مقاله روش جديدي براي حذف نويز تصاوير با استفاده از معادلات مشتقات جزيي ارايه شده است.
در به کارگيري معادلات مشتقات جزيي براي حذف نويز تصاوير از پارامتري به نام ضريب انتشار استفاده مي شود که انتخاب درست آن تاثير زيادي بر روي حذف نويز و حفظ لبه هاي تصوير دارد.
در مقالات موجود مقدار ضريب انتشار براي تصاوير مختلف بر اساس سعي و خطا به دست مي آيند.
اما در اين مقاله روشي ارايه مي شود که مقدار اين ضريب به صورت تطبيقي براي تصاوير در نظر گرفته مي شود.
روش ارايه شده در اين مقاله بر روي چندين تصوير استاندارد آزمايش شده است.
نتايج اين آزمايشات نشان مي دهند که روش ارايه شده در مقايسه با روش هاي موجود مبتني بر معادلات مشتقات جزيي عملکرد بهتري دارد.
گزارش:
کار حذف نویز مطابق مقاله انجام شده است.
یعنی از معادلۀ انتشار برای حذف نویز استفاده شده است.
ولی این مقاله اشکالاتی دارد، در واقع بعضی نتایج به دست اومده با نتایج ذکر شده در مقاله فرق میکند.
این تفاوت مربوط میشه به همان به دست آوردن ضریب بازگشتی.
کدهای مربوط به این قسمت و قسمتهای دیگر نوشته شده که درست کار میکنند ولی برخلاف اون چیزی که در مقاله گفته شده، k و var(d) اصلا رابطۀ مستقیم ندارند.
برای روشن شدن موضوع چند مثال ذکر میکنیم.
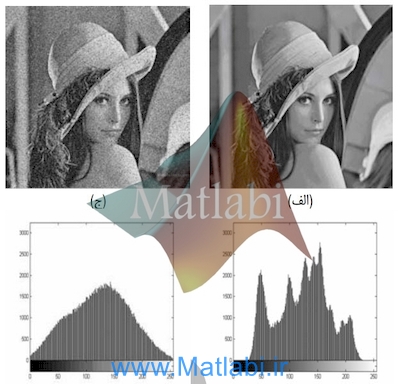
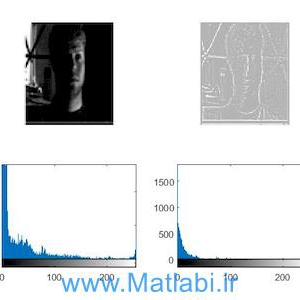
به این تصویرها نویز گوسی با میانگین صفر و واریانس 0.01 اضافه شده:
denoised Image noisy Image
Best k= 10;
V=var(d)=308.9420;
α= 0.032
Noisy Image Denoised Image
Best k=8;
V=var(d)=424.2730
α=0.0188 noisy Image

Noisy Image denoised Image
Best k=5;
V=var(d)=2327.6
α=0.0021
همانطور که مشاهده می شود، عمل حذف نویز به خوبی انجام شده ولی بین k و V، رابطۀ مستقیم وجود ندارد.
کلید واژه : پردازش تصویر, ضريب نفوذ, ضريب بازگشتي, معادلات مشتقات جزيي,
شبیه سازی
استفاده از ضريب انتشار تطبيقي براي حذف نويز تصاوير با استفاده از معادلات مشتقات جزيي
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.











دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.