آموزش انجام پروژه کنترل مدرن با متلب
آموزش انجام پروژه کنترل مدرن با متلب
در این آموزش متلب قصد داریم تمرین درس کنترل مدرن را بررسی و در متلب شبیه سازی کنیم:
تمرین شماره یک بصورت زیر است:
برای حل این تمرین از مثال حل شده فصل 6 کتاب کنترل مدرن دکتر علی خاکی صدیق کمک می گیریم
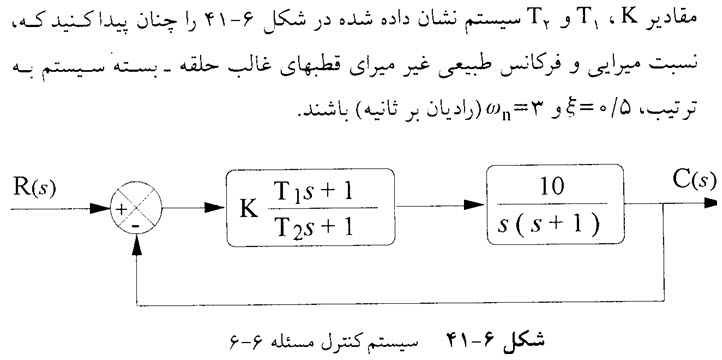
در این تمرین تابع تبدیل حلقه باز سیستم (بدون سیستم جبران ساز) به صورت زیر است
از جایی که 0.5=ξ و3=nω در این مسئله مشخص می باشد و با توجه به تابع تبدیل استاندارد که به صورت زیر است
با جایگذاری مقادیر داده شده مسئله در تابع تبدیل بالا تابع تبدیل برابر می شود با
که قطب های آن به صورت زیر بدست می آید
در واقع ما با طراحی این کنترل کننده باید به این قطب ها برسیم
برای براورده ساختن مشخصه های مسئله وبرای تغییر مسیر نمودار مکان ریشه ها به گونه ای که از قطب های حلقه-بسته (ذکر شده در بالا)عبور کند، جبران سازی طراحی خواهیم کرد.
Matlabi معتبرترین سایت انجام پروژه با متلب.
برای تعیین جبران ساز پیش فاز زاویه لازم φ جهت افزودن به مجموع زوایای قطبها و صفرهای حلقه-باز با یکی از قطبهای غالب حلقه –بسته مطلوب را پیدا می کنیم.مجموع این زوایا و زاویه φ باید باشد.
در سیستم فعلی، زاویه در قطب حلقه بسته مطلوب عبارتست از
از اینرو جبران ساز پیش فاز باید زاویه را فراهم آورد.
موقعیت قطب و صفری که این زاویه را فراهم می آورند،منحصر بفرد نیست.
یک جبران ساز مناسب (که با سعی و خطا بدست آمده است)عبارتست از
بهره از شرط دامنه تعیین می شود به عبارت دیگر از شرط دامنه داریم
با استفاده از شرط دامنه در قطب مورد نظر داریم
بهره برابر است با
پس به طور کلی اطلاعات بدست آمده برابر است با
ابتدا برای مشاهده مکان هندسی تابع تبدیل حلقه – بسته بدون کنترل کننده به صورت زیر عمل می کنیم
s=tf(‘s’);
gs=10/(s*(s+1));
sys1 = feedback(gs,+1);
rlocus(sys1)
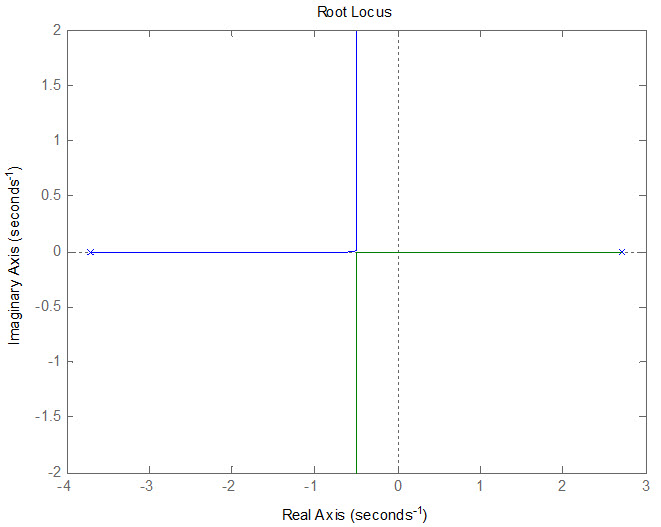
مکان هندسی حلقه- باز بدون کنترل کننده
مکان هندسی حلقه- بسته بدون کنترل کننده
برای بدست آوردن قطب های تابع تبدیل استاندارد به روش زیر عمل می کنیم
a=[1 3 9];
b=roots(a);
در ادامه برای تعیین زاویه مورد نظر از برنامه زیر استفاده شده
s=-1.5+2.59i;
z=10/(s^2+s);
r = abs(z);
theta = atan2(imag(z),real(z));
anglout = radtodeg(theta);
zaviye=180-anglout;
یعنی کنترل کننده ما باید زاویه بالا را جبران کند تا به جواب مطلوب برسیم که با بدست آوردن مقادیر t1 وt2 مورد نظر از طریق سعی وخطا به صورت زیر به زاویه مطلوب می رسیم
t1=3.7222; %40.8934
t2=0.45;
z1=((t1*s)+1)/((t2*s)+1);
r1 = abs(z1);
theta1 = atan2(imag(z1),real(z1));
anglout1 = radtodeg(theta1);
K بدست می آید با
k=1/abs(z1*z);
با دستورات زیر مکان هندسی ریشه های سیستم حلقه بسته را بدون کنترل کننده وهمینطور همراه با کنترل کننده در یک شکل رسم می شود
q=tf(‘s’);
gs=10/(q*(q+1));
gc=((k*(t1*q+1))/(t2*q+1));
sys1 = feedback(gs,1);
gg=series(gc,gs);
sys2=feedback(gg,1);
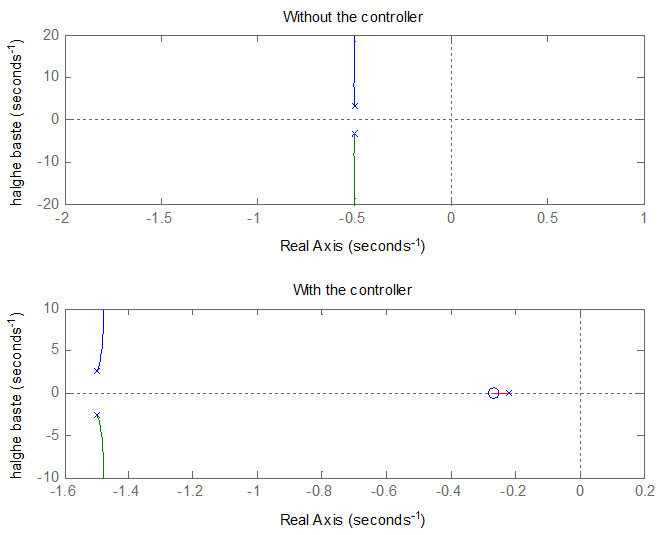
subplot(2,1,1); rlocus(sys1)
title(‘Without the controller’)
ylabel(‘halghe baste’)
subplot(2,1,2); rlocus(sys2)
title(‘With the controller’)
ylabel(‘halghe baste’)
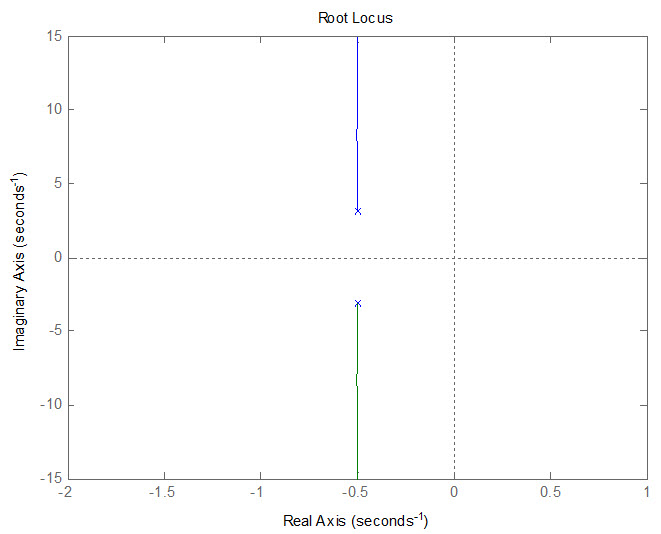
که به صورت زیر است
مکان هندسی ریشه های سیستم حلقه- بسته را بدون کنترل کننده وهمینطور همراه با کنترل کننده
همینطور اگر بخواهیم مکان هندسی حلقه-باز را رسم کنیم به شکل زیر است
figure
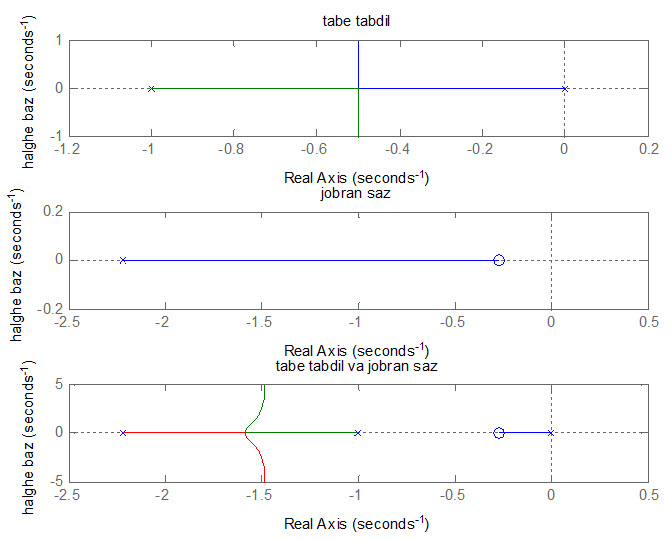
subplot(3,1,1); rlocus(gs)
title(‘tabe tabdil’)
ylabel(‘halghe baz’)
subplot(3,1,2); rlocus(gc)
title(‘jobran saz’)
ylabel(‘halghe baz’)
subplot(3,1,3); rlocus(gg)
title(‘tabe tabdil va jobran saz’)
ylabel(‘halghe baz’)
مکان هندسی حلقه-باز بدون کنترل کننده وهمینطور همراه با کنترل کننده
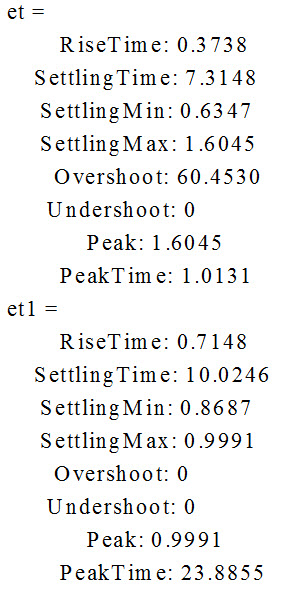
رسم پاسخ پله سیستم بدون کنترل کننده وبدون کنترل کننده و همینطور اطلاعات پاسخ پله آن به صورت زیر است به این صورت انجام می شود
et=stepinfo(sys1)
et1=stepinfo(sys2)
figure
subplot(2,1,1)
plot(step(sys1))
subplot(2,1,2)
plot(step(sys2))
پاسخ پله سیستم بدون کنترل کننده وبدون کنترل کننده
در پیوست برنامه متلب این تمرین وجود دارد که مرحله به مرحله توضیحاتی که داده شد در آن انجام شده و همچنین مکان هندسی حالات مختلف نیز رسم شده است.
- یک مثال عملی برای درس شناسایی سیستم با متلب
- سفارش شبیه سازی مقالات درس کنترل توان راکتیو
- نوشتن و کار با فایل MEX. در متلب توسط زبان ++C
- مقالات شبیه سازی شده با متلب کد جیg -بخش چهارم
- شناسایی سیستم غیر خطی ربات بازوی مسطح دو درجه آزادی توسط شبکه عصبی
.

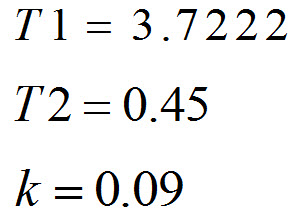






سلام خسته نباشید
این کدها میشه بدون دستورات اماده متلب نوشت؟
یعنی دستورات جزو تولباکس کنترل نباشن و با حلقه ها نوشته بشن؟
سلام میتونید درخواستتونو از طریق فرم ثبت سفارش سایت ارسال بفرمایید