آموزش مقدماتی Matlab – بخش سوم

آموزش مقدماتی متلب در چند بخش تهیه شده و می توانید در ویلاگ متلبی از آن بهره ببرید.
توابع ریاضی موجود در متلب:

Sin,cos,tan,cot

Log(x)

که همان

ln(x)

است.
Log10(x) که همان log در پایه ی 10 است.
Log2(x) که همان log در پایه ی 2 است.

Exp(x)=e^x

و توابع مثلثاتی بر حسب درجه: sind,cosd,sinh,cosh
اگر بعد از هر plot از Hold on استفاده کنیم ، تصویر plot را نگه می دارد .
اگر بخواهیم یک figure جدید باز کند میتوانیم قبل از plot بنویسیم figure و نام مورد نظر را هم جلوی آن بنویسیم که اگر نام را ننویسیم به صورت پیش فرض با عدد شماره گذاری می شود.
اگر اول برنامه close all بنویسیم، تمام پنجره های قبلی بسته می شود.
اعمالی که میتوان بر روی plot ها انجام داد:

Title(‘onvan’)

عنوان مورد نظر به شکل اضافه می شود.

Xlabel(‘ ‘)

Ylabel(‘ ‘)

برای محور ها برچسب گذاشته میشود.
Axis off & axis on محور های مختصات را خاموش و روشن میکند.
Grid on & grid off شکل را به صورت شبکه ای نمایش می دهد.
Axis equal زمان محور های مختصات x و y را مساوی میگیرد.
Axis normal به حالت عادی بر میگرداند .
Axis tight مختصات را به روی شکل fit میکند.
استفاده از دستور legend برای هر نمودار یک برچسب مشخص می کند .

Legend(‘ ‘,’ ‘)

اگر بخواهیم داخل plot و در مختصات خاصی ه مورد نظر ما است یک متنی نوشته شود:

Text(x,y,’matn’)

که x و y همان مختصات مورد نظرماست.
اگر از دستور gtext(‘matn’) استفاده کنیم ، بر روی figure که می رویم هر جا کلیک کنیم متن را برایمان مینویسد.
Rem reminder باقیمانده ی تقسیم a بر b rem(a,b)
Floor(a) به سمت عدد کوچکتر گرد می کند . همان براکت است.
Fix(a) قسمت اعشار را حذف میکند.
Min(a) مینیموم هر ستون را می دهد.
Max(a) برای هر ستون یک متکسیمم می دهد.
اگر بخواهیم مقادیر ی ماترس را نرمالیزه کنیم برای این کار ابتدا باید max همه ی مقادیر را به دست بیاوریم و بعد تمام مقادیر را تقسیم بر آن max میکنیم.
Sort(a) تمام ستون ها را از کوچک به بزرگ مرتب می کند.
Mean(A) میانگین تمتم ستون ها را به ما می دهد.
Meanz(a) میانگین تمام درایه ها را به ما می دهد.
Dot(a,b) ضرب داخلی که نتیجه ی آن یک عدد است.
Cross(a,b) ضرب خارجی که نتیجه ی آن یک بردار است.

Gcd(a,b) Greatest common divisor

بزرگترین مقسوم علیه مشترک را نمایش می دهد.

Lcm(a,b) least common multiplier

کوچکترین مضرب مشترک دو عدد را نمایش می دهد.
اگر روی یک تابع راست کلیلک کنیم و open selection را بزنیم کل دستورات mfile که نوشته شده تا این تابع انجام پذیرد را می بینیم.
برای اینکه در کار با ماتریس ها بخواهیم ضرب یا تقسیم درایه ها را نظیر به نظیر انجام بدهیم باید از .* و ./ استفاده بکنیم.

Isprime(b)

آیا عدد اول هست یا نه
اگر یک بدهد یعنی عدد مورد نظر اول بوده است و اگر صفر بدهد یعنی عدد اول نبوده است.
مثال:
اعداد اول 1 تا 1000 را مشخص کنید:

Clc

Clear all

T=1:1000;

A=isprime(t);

r=t.*A;

r’

علامت ‘ میگذاریم تا ستونی نمایش دهد و راحت تر ببینیم.
اعداد مختلط:
اعداد مختلط در متلب به صورت a+b*j و یا a+b*i نمایش داده میشوند. (باید i و j به عنوان متغیر قبلاً استفاده نشده باشند)
Z=complex(a,b) عدد مختلط را می خواند.
Real(z) برای مشاهده ی قسمت حقیقی
Imag(z) برای مشاهده و قسمت موهومی
Abs(z) اندازه ی عدد مختلط را به ما می دهد.
Angle(z) زاویه ی عدد مختلط را به ما می دهد . بر حسب زاویه
X*(180/pi) رادیان را به زاویه میبرد.
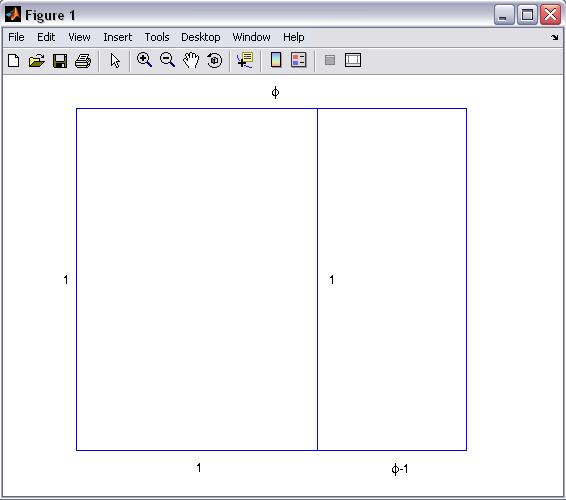
مثال:رسم مستطیل طلایی: golden rectangle
این مستطیل برای معماری کاربرد دارد.در این مستطیل نسبت طول به عرض برابر است با:

1+sqrt(5))/2)

که حاصل آن برابر است با تقریبا 1/6
اگر بنا ها با این نسبت ساخته شوند خیلی زیبا تر به چشم می آیند.
اگر از مستطیل طلایی یک مربع جدا کنیم، شکل باقیمانده خود یک مستطیل طلایی است.
طریقه ی ایجاد :
یک مربع میکشیم و وسط یک ضلع را مییابیم به اندازه ی فاصله ی این نقطه ی وسط تا ضلع روبرویش یک کمان میزنیم و سپس ادامه می دهیم
ابتدا یک mfile باز می کنیم:

clc

clear all

phi=(1+sqrt(5))/2;

x=[0 phi phi 0 0]

y=[0 0 1 1 0]

plot(x,y)

x1=[1 1]

y1=[0 1]

hold on

plot(x1,y1)

axis off

text(-0.05,0.5,’1′)

text(0.5,-0.05,’1′)

text(phi/2,1.05,’\phi’)

text(1+(phi-1)/2,-0.05,’\phi-1′)

text(1.05,0.5,’1′)

set(gcf,’color’,’w’)

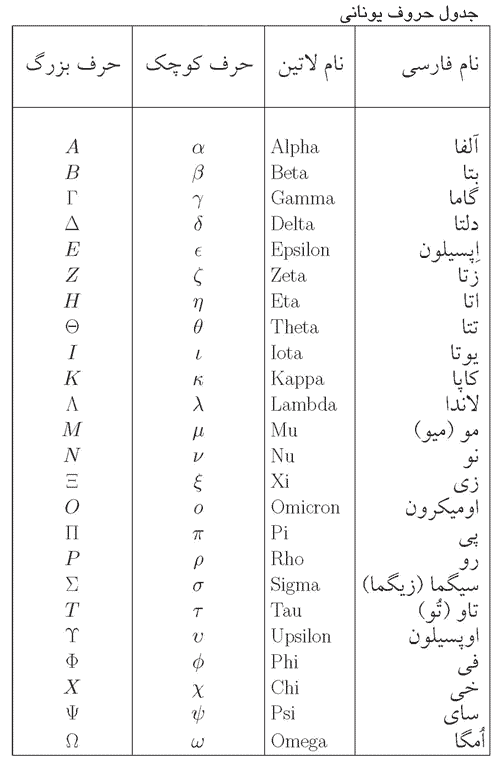
برای نمایش حروف یونانی در متلب فقط در plot ها میتوانیم با استفاده از نام انگلیسی آن ها به همراه \ این کار را انجام دهیم.
مطابق phi در رسم مستطیل بالا.

رسم چند plot در یک figure :

Subplot(n,m,x)

که در این جا n تعداد سط ها ، m تعداد ستون ها x شماره ی plot است.
برای title و یا label گذاشتن در اینجا باید بعد از هر plot این کار را انجام بدهیم.
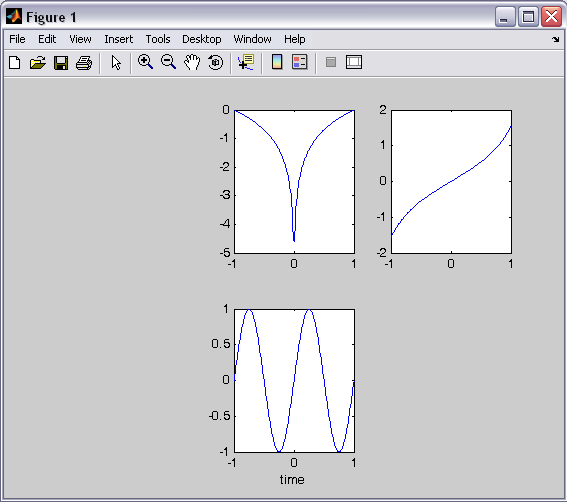
در یک figure 6 قسمتی، در plot پنجم سینوسی و در plot دوم لگاریتمی و در plot سوم tan رسم کنید:

clc

clear all

close all

fs=100;

t=-1:1/fs:1;

y1=sin(2*pi*t);

subplot(2,3,5)

plot(t,y1),xlabel(‘time’)

y2=log(t)

subplot(2,3,2)

plot(t,y2)

y3=tan(t)

subplot(2,3,3)

plot(t,y3)

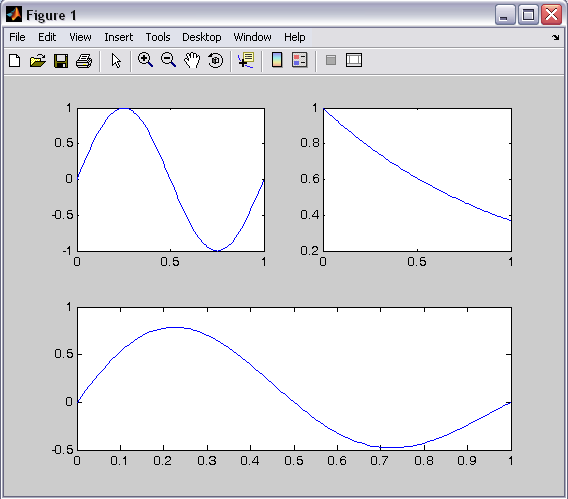
اگر بخواهیم یکی از subplot ها مثلا به اندازه ی 2 subplot باشد یعنی بزرگتر از subplot های دیگر باشد، از روش زیر استفاده میکنیم.در مثال پایین plot سومی در دو جایگاه سوم و چهارم قرار میگیرد و به اندازه ی دو برابر سایر plot هاست.

clc

clear all

close all

fs=100;

t=0:1/fs:1;

x1=sin(2*pi*t);

x2=exp(-t);

x3=(x1.*x2);

subplot(2,2,1)

plot(t,x1)

subplot(2,2,2)

plot(t,x2)

subplot(2,2,3:4)

plot(t,x3)

نمودار میله ای:
bar(x,f(x))

نمودار گسسته:

Stem(x,f(x))

نمودار پلکانی:

Stairs(x,f(x))

نمودار هیستوگرام:

Hist(f(x),x)

توابع سمبولیک یا آنالوگ:
چندجمله ای: polynomial
A=[2 4 6 8] معرف چند جمله ای درجه 3 است.

A=[an,a(n-1),a(n-2),…,a0]

معرف ضرایب چند جمله ای درجه n است.
X=roots(a) که در آن a یک بردار است، ریشه ها را به ما می دهد.
Poly(x) ضرایب را به ما میدهد.
به طوری که roots و poly برعکس هم عمل میکنند.
هر گاه از poly استفاده کنیم، همیشه ضریب an را 1 میگیرد و بقیه را تقسیم بر ضریب an میکند تا ضریب an 1 شود.

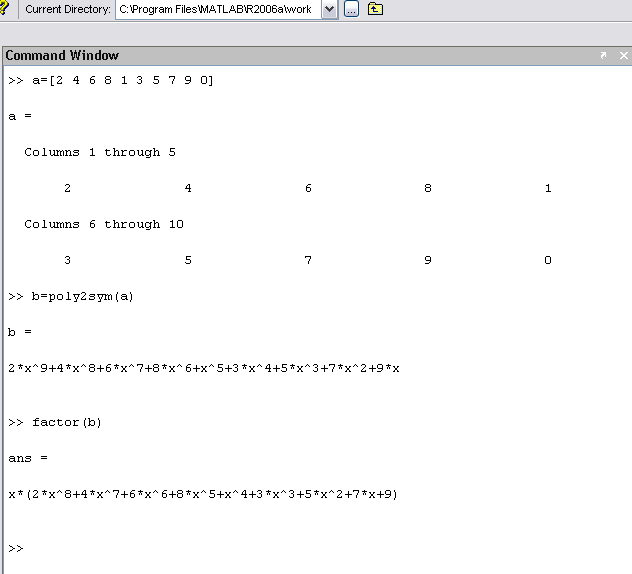
برای تبدیل polynomial به سمبولیک:
poly2sym()

A=[2 4 6 8]

Poly2sym(a)

Ans=

2*x^3+4*x^2+6*x+8

Syms x بعد از نوشتن این عبارت enter میزنیم و x را به عنوان یک سمبل در نظر میگیرد.
حالا میتوان از این سمبل استفاده کرد و سمبل های دیگر ساخت.

Y=sin(x)

رسم توابع سمبولیک:

Ezplot(y)

که در اینجا y و یا هر عبارت داخل پرانتز باید سمبولیک باشد.

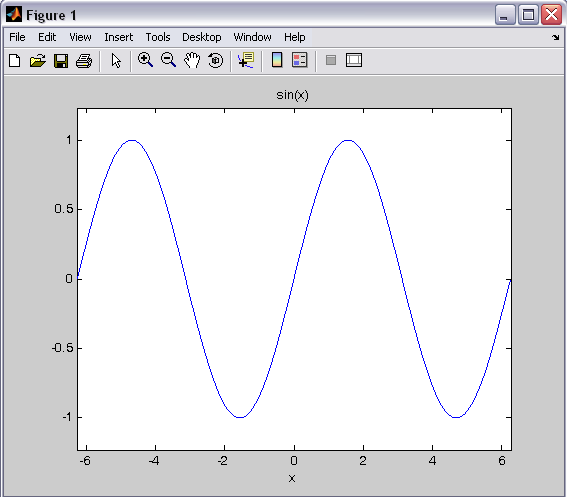
Syms x

Y=sin(x)

Ezplot(y)

به صورت پیش فرض بین -2pi و 2pi رسم میکند.
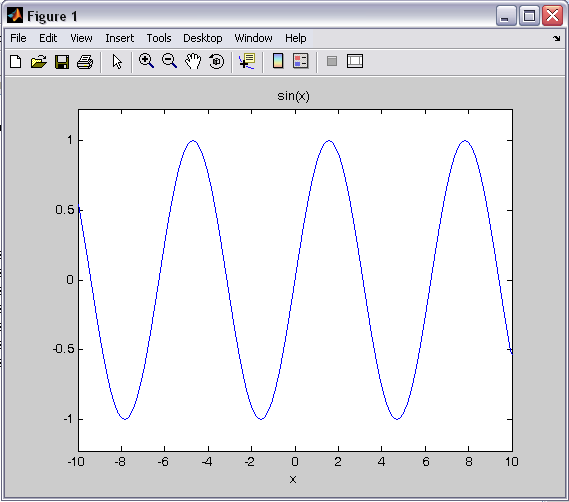
اگر بخواهیم پیش فرضش را تغییر بدهیم:

Ezplot(y,[-10,10])

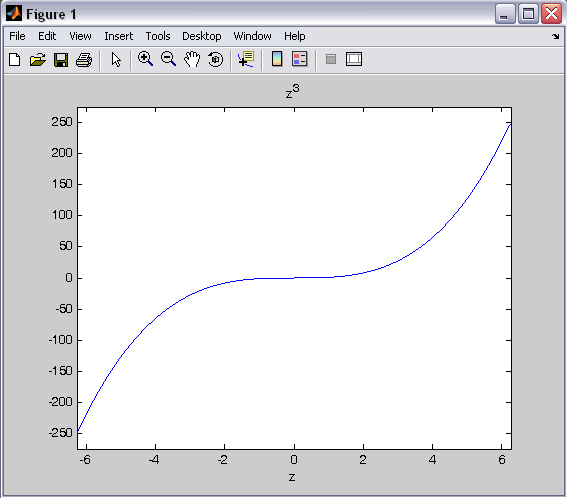
اگر متغیر قبلا سمبولیک نشده باشد میتوانیم داخل ” قرار بدهیم.

Ezplot(‘z^3’)

که در این حالت میتوانیم برای y هم مختصات تعریف بکنیم.

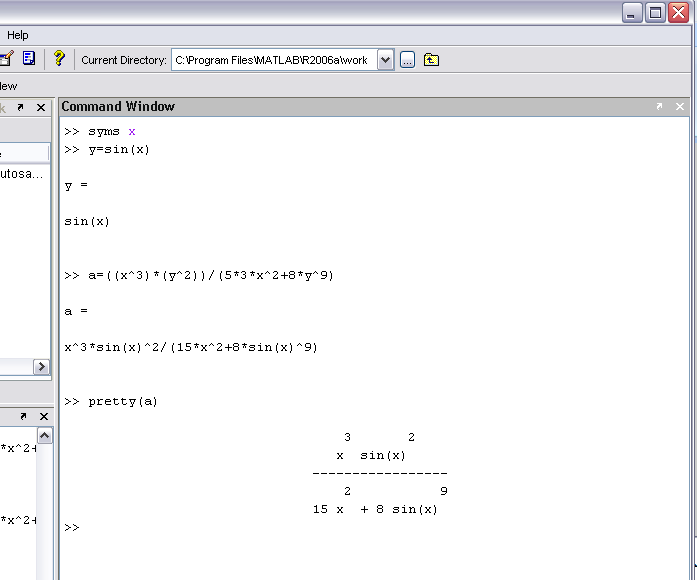
Pretty(a)

به حالت دست نویس نشان میدهد.

Simple(y) بسط ها را نشان می دهد.
Factor(a) اگر سمبلی قابل فاکتور گرفتن باشد از آن فاکتور میگیرد.

Conv(a,b) که در آن a و b ضرائب چند جمله ای هستند، ضرب convolution انجام می دهد.
Convolution وقتی به حوزه ی فرکانس برود به ضرب تبدیل میشود. برای فیلتر کاربرد دارد.
Deconv(a,b) تقسیم است.
مشتق چند جمله ای در بحث چند جمله ای:
Polyder(a)
که در این جا a ضرایب چند جمله ای ست.

Polyder(a,b)

مشتق ضرب چند جمله ای است.

[A B]=polyder(a,b)

مشتق تقسیم چند جمله ای است.
ارزیابی چند جمله ای ها:

Polyval(a,x0)

عدد با بردار x0 را در چند جمله ای a مقدار دهی میکند.

مقدار دهی در حالت سمبولیک:

Subs(f,’x’,a)

عدد a را در تابع f به جای x قرار می دهد.

می توانیم به جای یک متغیر چند مقدار مختلف بگذاریم:
مثلا :

F=x^z-sin(x+z)

Subs(f,'[x y z]’,[1 pi/2 2])