مدل فرایند گاورنر 4درجه آزادی جهت کنترل سرعت توربین

مدل فرایند گاورنر 4درجه آزادی جهت کنترل سرعت توربین

مدل فرایند گاورنر جهت کنترل سرعت توربین به فرم زیر درنظر گرفته شده است.
همچنین برای جبرانسازی افت فرکانس سیستم از یک دروپ کنترل کننده انتگرالی برای حذف خطای حالت ماندگار استفاده می گردد.

کد نوشته شده در نرم افزار متلب به صورت زیر می باشد. (Parameters.m)
 

clc

% Dynamic Model Parameters:

Tt = 0.3;

Th = 0.1;

Fs = 60;

R  = 0.05*Fs;

H  = 3;

D  = 1.2125;

% Dynamic Model;

s = tf(‘s’);

Gdroop = (-1/(R*s))

Tfgov  = (1/(Th*s+1));

Tftur  = (1/(Tt*s+1));

Tfgen  = (Fs/(2*H*s+D));

Plant  = Tfgen*Tftur*Tfgov*Gdroop;

t=0:0.1:20;

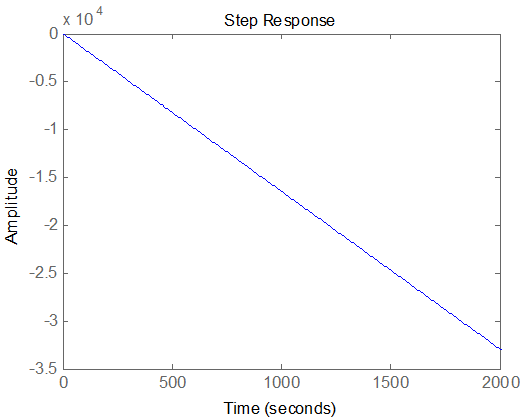
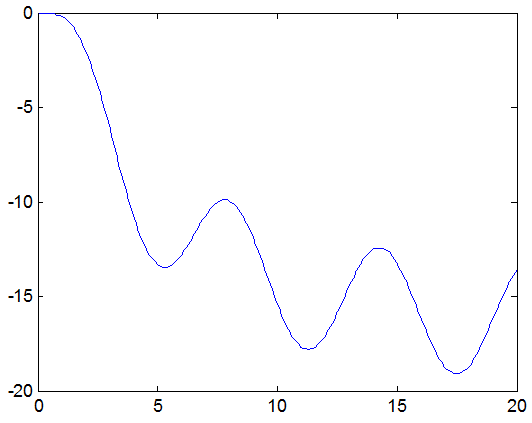
با تعریف ورودی پله و سیگنال سینوسی به صورت زیر نتایج به فرم زیر قابل نمایش است.
 

t=0:0.1:20;

u=sin(t);

step(Plant);

y = lsim(Plant,u,t);

شکل 1- پاسخ پله سیستم

شکل 2 – پاسخ سیستم به ورودی سینوسی

بر اساس روش های کنترل کلاسیک در اینجا PID به طراحی کنترل کننده مناسب جهت پایدارازی سیستم و ردیابی ورودی مرجع پرداختیم که کنترل کننده حاصل به شکل زیر می باشد.

• شبیه سازی سیستم درایو کرامر استاتیکی با متلب
• پروژه شناسایی سیستم با متلب
• طراحی و پیاده سازی OCR دست نویس فارسی با استفاده از عناصر ابتدایی تشکیل دهنده حروف
• الگوریتم ملخ ها
• دانلود نرم افزار متلب Mathworks Matlab 2017a
• دانلود نرم افزار متلب MATHWORKS MATLAB R2018B

اساس تنظیم این روش مبتنی بر طراحی زیگلر- نیکولز می باشد.

شکل 3- شبیه سازی سیستم با کنترل کنندهPID

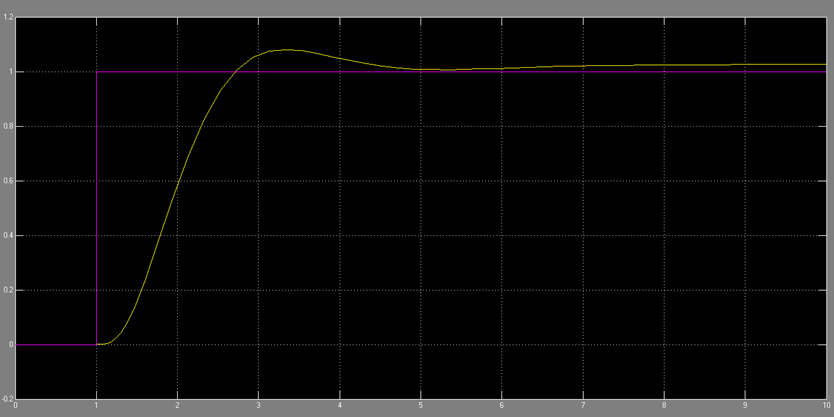
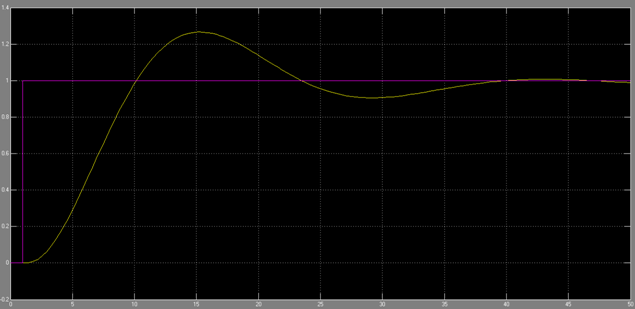
شکل 4 – پاسخ سیستم به ووردی پله در حضور کنترل کننده PID

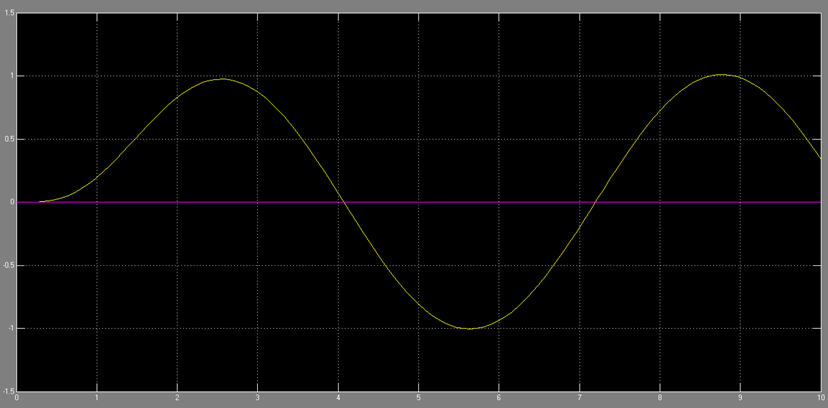
شکل 5 – پاسخ سیستم به ووردی سینوسی در حضور کنترل کننده PID

جهت طراحی مناسبترین کنترل کننده ، جبران ساز پیش فاز – پس فاز را بکار برده ایم.
همچنین جهت تنظیم پارامترهای این کنترل کننده از IMC استفاده کرده ایم.
با توجه به نتایج نشان داده شده در شکل زیر کنترلر به عنوان تنظیم کننده عملرد بهتری نسبت به حالت ردیابی دارد.

شکل 6- شبیه سازی سیستم با جبران ساز پیش فاز – پس فاز

شکل 7 – پاسخ سیستم به ووردی پله در حضور جبران ساز پیش فاز – پس فاز

شکل 8 – پاسخ سیستم به ورودی سینوسی در حضور جبران ساز پیش فاز – پس فاز

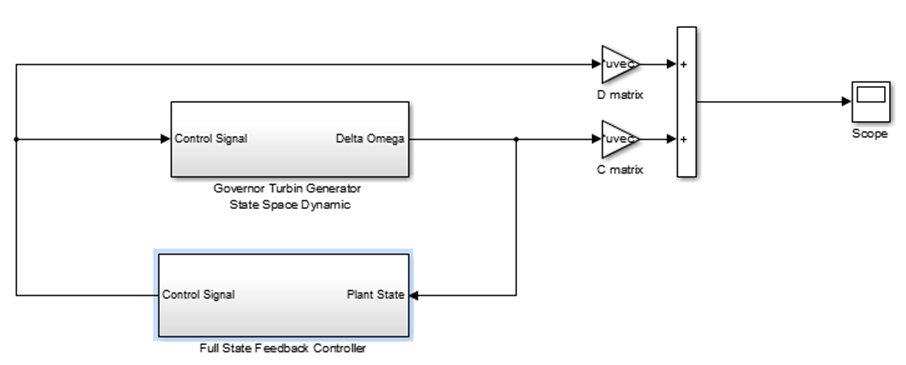
در این قسمت فضای حالت در متلب به صورت زیر تعریف می گردد:

% Convert Plant to State Space ;

Pss = ss(Plant);

[A,B,C,D] = ssdata(Pss)

شکل 9- شبیه سازی سیستم برای طرحی فیدبک حالت

در این حالت با توجه به طراحی انجام شده در فضای حالت در مقایسه با توابع تبدیل توانایی اعمال شرایط اولیه و بررسی پاسخ سیستم نسبت به شرایط اولیه در حالت ورودی صفر را داریم.
این کنترل کننده به لحاظ عملکردی دارای سرعت پاسخ بیشتری می باشد.
همچنین با تنظیم بهره فیدبک حالت کنترلی هرچه قدر گین های بزرگتری انتخاب کنیم قطب های حلقه بسته سیستم در مکان دورتری قرار خواهد گرفت و در نتیجه سیستم پایدار تر خواهد شد.

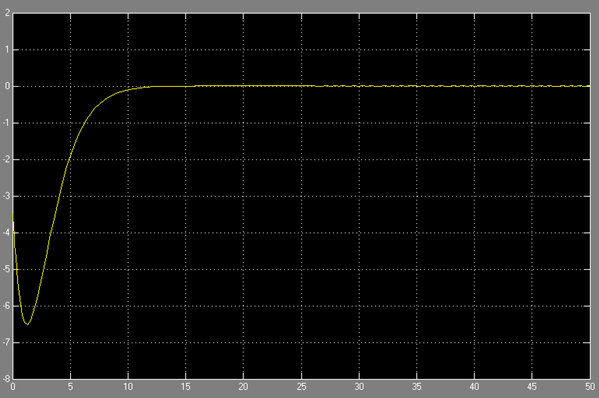
شکل 10 – پاسخ سیستم به شرایط اولیه در حضور کنترل فیدبک حالت کامل

در مرحله بعد بهینه سازی پارامترهای کنترل کننده با تعریف توابع هدف مختلفی در متلب قابل انجام است.
اکثر روشهای بهینه سازی کلاسیک مبتنی بر سیگنال خطای سیستم می باشد .
در روش ITAE با در نظرگیری انتگرال  قدرمطلق خطا پارامترهای k را طوری محاسبه می نماییم که مقدار تابع هدف مورد نظر حداقل گردد. علت استفاده از قدر مطلق در این معیار جلوگیری از صفر شدن اثر سطوح مثبت و منفی می باشد.
با توجه به فایل شبیه سازی که در شکل نمایش داده شده است و  تابع تعریف شده در فایل ITAE.m با اجرای دستور زیر فرایند بهینه سازی ضرایب PID آغاز می گردد.

>> global P I

P = var(1);

I = var(2);

[t,x,y] = sim(‘PIDcontrolTIAE’,50);

[zn,fval,exitflag]=fminsearch(‘ITAE’,[8,8],optimset(‘MaxIter’,100))

شکل 11- شبیه سازی سیستم برای تنظیم ضریب PID به روش ITAE

شکل 12 – پاسخ سیستم به ورودی پله در حضور کنترلPID و کاربرد روش ITAE

میخواهیم بر اساس الگوریتم رگولاتور بهینه خطی درجه دو LQR در متلب بهینه ترین گین ها را جهت فیدبک نمودن حالت های سیستم طراحی نماییم.
از آنجایی که هرچه K را بزرگتر انتخاب کنیم قطبهای حلقه بسته در مکان دورتری از محور موهومی قرار می گیرند اما این مشکل نیز به وجود خواهد آمد که سیگنال های کنترل متناسب با این بهره های بزرگ ، بزرگ خواهند شد و با توجه به محدودیت عملگرهای سیستم امکان ناپایداری وجود خواهد داشت.
بنابراین با روش طراحی کنترلر بهینه بهترین بهره ممکن جهت جایابی قطبهای حلقه بسته سیستم را پیدا می کنیم.

شکل 13-  پاسخ سیستم به شرایط اولیه با در نظ گرفتن کنترل کننده LQR

با توجه به طراحی کنترل کننده فیدبک حالت سیستم نیاز به اندازه گیری همه حالت های سیستم جهت فیدبک نمودن دارد.
اما در عمل تنها تعداد محدودی از خروجی ها قابل اندازه گیری هستند بنابراین با طراح رویت گر حالت به تخمین حالت های سیستم می پردازیم.

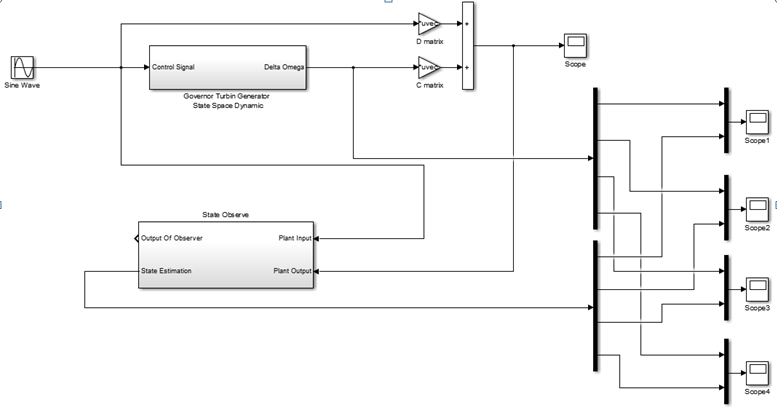
شکل 14 – شبیه سازی رویتگر کامل

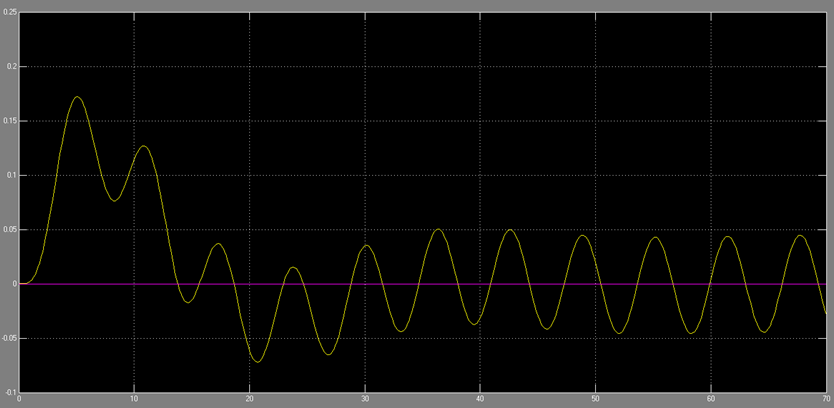
شکل 15- مقایسه حالت های  تخمینی (پایین)  با حالت واقعی سیستم (بالا)

با توجه به طراحی بهره رویتگر قطبهای حلقه بسته سیستم دینامیکی رویتگر می توانند در هر نقطه موردنظر ما قرار گیرند.

در ایجا نیز مانند طراحی فیدبک حالت انتخاب بهره های بزرگ باعث دور شدن قطبهای رویتگر از محور موهومی و سریع شدن پاسخ خمین رویتگر خواهند شد.

اما با توجه به وجود نویز اندازه گیری سنسورها بزرگ بودن مقدار بهره رویتگر باعث تقویت این نویز و کاهش عملکرد حالت های تخمین زده شده می گردد.

بنابراین در اینجا نیز انتخاب بهینه بهره رویتگر مساله مهمی می باشد.

شکل 16- مقایسه حالت های  تخمینی (پایین)  با حالت واقعی سیستم (بالا) – پاسخ واگرا

هدف از طراحی رویگر کاهش یافته ، کاهش مرتبه دینامیکی رویتگر با اجتناب کردن از تخمین حالت یکی از متغیرها که اندازه گیری آن با سنسور و هزینه پایین و بدون نویز مقدور می باشد است.
اما در سیستم در نظرگرفته شده برای دینامیک گاورنر و با توجه به اینکه تنها یک خروجی قابل اندازه گیری برای اعمال به رویتگر و بهبود تخمین حالت های سیستم با بروز کردن مقادیر داریم بنابراین استفاده از رویتگر کاهش یافته به معنای اجتناب کردن از اعمال ورودی سنسور به رویتگر می باشد و این نکته مانع از بهبود عملکرد رویتگر با بروز نمودن پارامترها است.
وجود نویز در سنسور با توجه به فیدبک نمودن خروجی اندازه گیری شده به رویت گر باعث تخمین حالت های سیستم همراه با مقداری نویز و متعاقبا کاهش عملکرد سیستم رویتگر و در نتیجه سیستم کنترل کننده فیدبک حالت خواهد شد.
جهت دانلود برنامه متلب آموزش داده شده اینجا را کلیک کنید
governer_matlabi