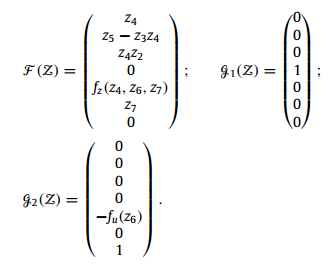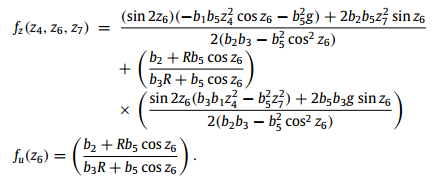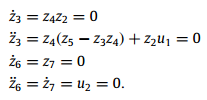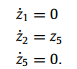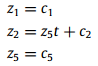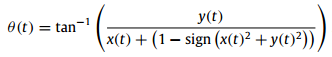توضیحات
Nonlinear control of mobile inverted pendulum
مقاله مربوط به درس کنترل غیر خطی (خطی سازی با فیدبک) را تا آخر بخش 3.2 یعنی homing toward the target با توجه به توضیحات فایل ضمیمه با نرم افزاز سیمولینک متلب انجام شده و تشریح پاسخها انجام شده
گزارش به شرح زیر است:
این شبیه سازی بر اساس درخواستی که در فایل پی دی اف زیر وجود دارد تهیه شده است:
قسمت دوم
1-(X,Y,Z) چارچوب نامی
2-(Xv,Yv,Zv) چارچوب مختصات وسیله است
3- (Xb,Yb,Zb) مختصات پاندول
4-(Xa,Ya,Za) مختصات موازی مختصات (X,Y,Z) است به مرکز سیستم
همانطور که در شکل اول مقاله مشاهده میشود زاویه مربوط به زاویه پاندول و زاویه مربوط به جهت سیستم میباشد.
قسمت سوم
مدل فضای حالت سیستم MIP به صورت زیر نوشته میشود.
که و x و y مربوط به مختصات مکان سیستم جهت سیستم و سرعت زاویه سیستم ، زاویه پاندول و سرعت زاویه ای پاندول و v سرعت خطی سیستم هستند.
قسمت چهارم
برای طراحی کنترل کننده از تبدیل زیر برای ساده سازی مدل استفاده میشود.
با در نظر گرفتن این تبدیلات معادلات حالت زیر بدست میآید.
ورودی های کنترل را به صورت زیر در نظر بگیرید :
با فرض بالا داریم:
پس داریم:
قسمت پنجم
معادلات خروجی مربوط به سیستم به صورت زیردر نظر گرفته میشود.
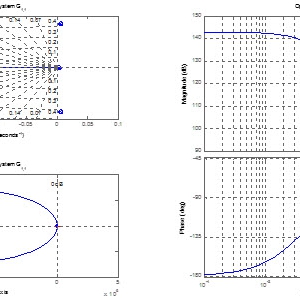
برای محاسبه دینامیکهای صفرسیستم عبارت را محاسبه میکنیم. که نتیجه آن به صورت زیر میباشد.
از این عبارت نتیجه زیر حاصل میشود.
با درنظر گرفتن مقادیر بالا دینامیک های داخلی به صورت زیر بدست میآیند
که با حل آنها داریم:
که نشان دهنده ناپایداری دینامیک های داخلی میباشد.
قسمت ششم
این بخش طراحی از سه قسمت تشکیل شده است. هدف اصلی از کنترل خانه یابی چرخش روبات به موقعیت مورد نظر ، حرکت به سمت موقعیت هدف در راستای یک خط راست بین نقطه اولیه و نقطه انتهایی (نقطه هدف) میباشد که این امر با پایدار سازی حالت z3 بدست می آید.
زمانی این حالت پایدار میشود که مقدار نقطه تعادل خود یعنی صفر میل کند. با صفر قرار دادن این رابطه داریم :
که همان جهت مورد نظر ما در طراحی این کنترل کننده میباشد. حال برای کنترل جهت سیستم باید زیرسیستم زیر پایدار گردد.
که با در نظر گرفتن ورودی کنترلی به صورت زیر این زیر سیستم نیز پایدار میگردد.
فقط چون جهت سیستم برای x=0 و y=0 مبهم است لذا رابطه زیر برای آن تعریف میگردد.
برای پایدار سازی زاویه پاندول نیز از قانون کنترل زیر استفاده میشود
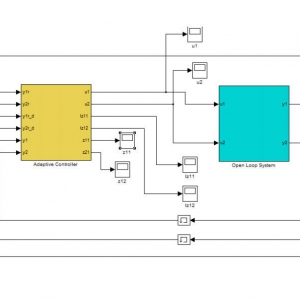
که در این روابط k1 تا k4 همگی مثبت هستند. با در نظر گرفتن این ورودی های کنترلی سیستم حلقه بسته به صورت زیر بدست می آید
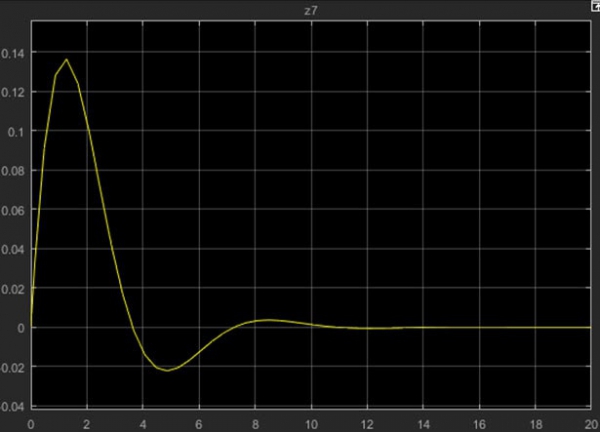
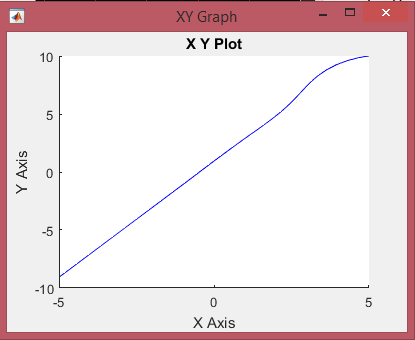
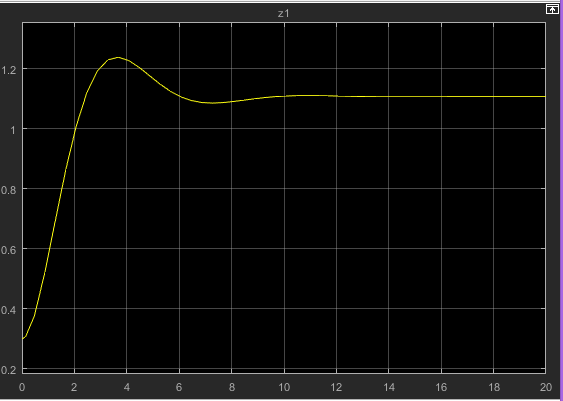
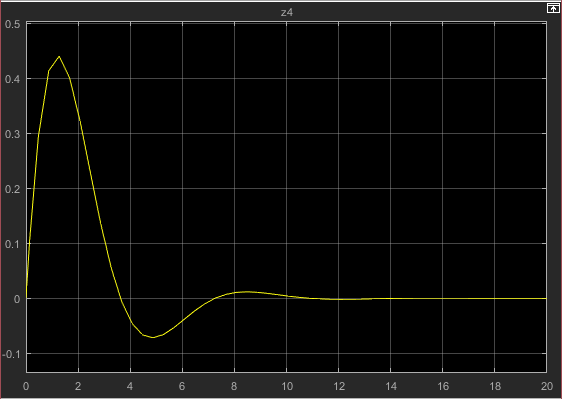
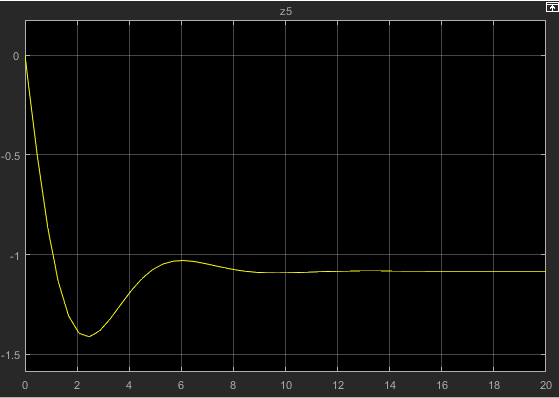
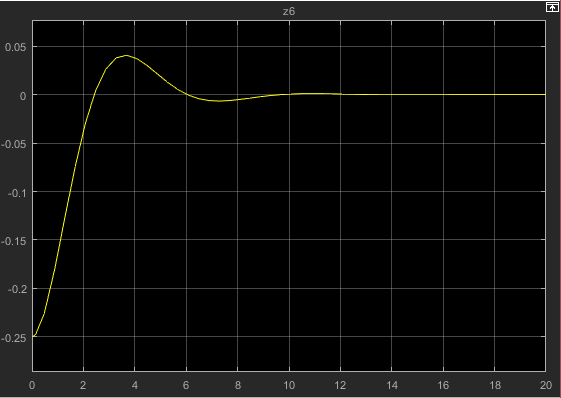
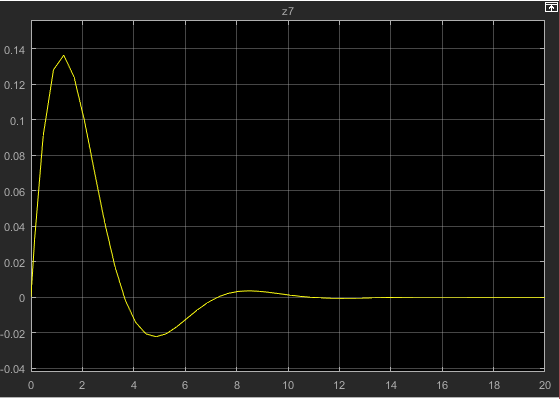
کد مربوط به این سیستم حلقه بسته با توجه به شرایط اولیه x و y در شکل های 4 تا 7 به صورت زیر میباشد. مقادیر درنظرگرفته شده برای زوج (x,y) به ترتیب به صورت (-5,-10),(5,-10),(-5,10),(5,10) میباشد. که 4 ربع مختصات را در برمیگیرد.
function dz=Third_quarter(z1,z2,z3,z4,z5,z6,z7)
…
نتایج حاصل از این شبیه سازی برای ربع اول به صورت زیر میباشد. که به ترتیب شکل 4 میباشد
به همین ترتیب شبیه سازی برای 4 ربع انجام شده است. و نتایج آن قابل مشاهده است.
کلید واژه :
Mobile inverted pendulum (MIP), Nonlinear control, Underactuated system
شبیه سازی
Nonlinear control of mobile inverted pendulum
توسط کارشناسان سایت متلبی تهیه شده و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.