توضیحات
Improved Invasive weed optimization Algorithm (IWO) Based on Chaos Theory for Optimal design of PID controller
شبیه سازی الگوریتم بهینه سازی علفهای هرز مهاجم بهبود یافته بر اساس تئوری آشوب برای طراحی کنترلکننده PID بهینه
دارای شبیه سازی در محیط ام فایل متلب است.
دارای گزارش ورد 45 صفحه ای و همچنین ویدیو نحوه اجرای برنامه متلب است.
توضیحات پروژه
در اینجا توضیحاتی از پروژه قرار داده شده. با خرید این محصول فایل های شبیه سازی و گزارش کامل را دریافت خواهید نمود.
شبیه سازی در 6 پوشه مجزا انجام شده است. مطابق شکل 3 مقاله برای تابع sphere , تابع Rastrigin , تابع Griewank و در بخش D مقاله برای تابع EF10 و بخش E مقاله برای تابع EASOM و در بخش 5 مقاله بهینه سازی کنترلر PID قرار گرفته است.
در هر پوشه IWO ساده, IWO بهبود یافته, IWO آشوب , IWO آشوب بهبود یافته وجود دارد. همچنین امکان مقایسه این روش ها با هم نیز وجود دارد.
در فایل گزارش این پروژه کد متلب کامل توضیح داده شده است.
مقدمه:
علف هرز پدیدهای است که به دنبال بهینگی میرود و بهترین محیط را برای زندگی پیدا میکند و به سرعت خودش را با شرایط محیطی وفق میدهد و در برابر تغییرات مقاومت میکند. با در نظر گرفتن این ویژگیها، یک الگوریتم قدرتمند توسعه مییابد. الگوریتم بهینهسازی علفهای هرز مهاجم (IWO)[1] یک روش بهینهسازی تکاملی مبتنی بر جمعیت است که از رفتار تجمعی علفهای هرز الهام میگیرد. از میان پارامترهای IWO، انحراف استاندارد بطور قابل ملاحظهای بر روی عملکرد الگوریتم اثر میگذارد. بنابراین، نگاشت آشوب میتواند در پارامتر انحراف استاندارد استفاده شود. این امر مبنای توسعه الگوریتم IWO آشوب میباشد. عملکرد روش علف هرز مهاجم آشوب بر روی پنج تابع معیار با استفاده از نگاشت آشوب منطقی مورد بررسی قرار خواهد گرفت. علاوه بر این مسأله تنظیم پارامترهای کنترلکننده PID برای یک موتور DC با استفاده از روش بهبود یافته مورد بحث قرار خواهد گرفت. نتایج آماری بر روی مسائل بهینهسازی نشان میدهند که روش علفهای هرز مهاجم آشوب بهبود یافته نرخ همگرایی سریعتری و دقت بالاتری دارد.
مفاهیم اساسی الگوریتم علفهای هرز مهاجم:
الگوریتم فرا ابتکاری علفهای هرز مهاجم یک الگوریتم بهینهسازی مبتنی بر جمعیت است که مقدار بهینه فراگیر (کلی) یک تابع ریاضی را از طریق قابلیت تقلید و خاصیت تصادفی کلنی علفهای هرز مییابد. علفهای هرز گیاهان مقاومی هستند که رشد تهاجمی آنها تهدید جدی برای محصولات زراعی است. آنها برای تغییرات محیطی بسیار مقاوم و تطبیقپذیرند. بنابراین، با در نظر گرفتن مشخصات آنها یک الگوریتم بهینهسازی مقاوم حاصل میشود. این الگوریتم سعی به تقلید مقاومت، تطبیقپذیری و خاصیت تصادفی تجمع علفهای هرز را دارد. این روش از پدیدهای در کشاورزی بنام کلنیهای علفهای هرز مهاجم الهام میگیرد. مطابق یک تعریف متداول، علف هرز گیاهی است که ناخواسته رشد میکند. اگرچه، اگر همان گیاه در ناحیهای رشد کند که با نیازها و فعالیتهای انسانی در ارتباط باشد ممکن است در برخی نواحی کاربرد و منافعی داشته باشند. در [1] یک الگوریتم بهینهسازی عددی ساده پیشنهاد شده است که الگوریتم بهینهسازی علف هرز مهاجم نام دارد. این الگوریتم ساده اما مؤثر در همگرایی به جوابهای بهینه با استفاده از ویژگیهای پایه مثل کاشت، رشد و رقابت در یک کلنی علف هرز میباشد.
[1] invasive weed optimization algorithm
الگوریتم بهینه سازی علفهای هرز مهاجم آشوب (نامنظم) بهبود یافته:
الگوریتمهای بهینهسازی بر اساس نظریه آشوب از روشهای جستجوی تصادفی استفاده میکنند. این الگوریتمها از الگوریتمهای رقابت تکاملی و الگوریتمهای هوشمند مبتنی بر جمعیت متفاوت هستند. بعلت ماهیت غیر رقابتی نظریه آشوب، جستجوهای کلی در سرعت بیشتری از جستجوهای تصادفی اجرا میشوند که مربوط به احتمالات هستند. بعلاوه تنوع جمعیت بهتر خواهد شد. همچنین اطمینان حاصل میشود که جمعیت اعضا کل ناحیه جستجو را در بر بگیرد. بنابراین، پاسخهای بهینه یا نزدیک به بهینه در میان جمعیت خواهند بود. یکی از نگاشتهای آشوب مشهور، نگاشت آشوب منطقی است. این تابع یک چندجمله ای درجه دوم است.
همگرایی الگوریتم بهینه سازی علف هرز مهاجم آشوب بهبود یافته:
این مطالعات بر روی نشان دادن قابلیت IWO آشوب بهبود یافته در موقعیت کمینه کلی توابع پیوسته تمرکز دارند. Sphere، Griewank و Rastrigin سه نمونه تابع معیار هستند. ویژگی آنها در شکل 3 نشان داده شده است.
نتایج کمینه سازی تابع Sphere با 30 اجرا توسط الگوریتمهای IWO مختلف
| عملکرد | IWO ساده | IWO بهبود یافته | IWO آشوب | IWO آشوب بهبود یافته |
| میانگین هزینه ها | 0648/0 | 0434/0 | 0426/0 | 0238/0 |
| بهترین هزینه ها | 10-16×34/9 | 0 | 10-17×78/4 | 0 |
| بدترین هزینه ها | 9138/681 | 9640/617 | 1232/376 | 4613/301 |
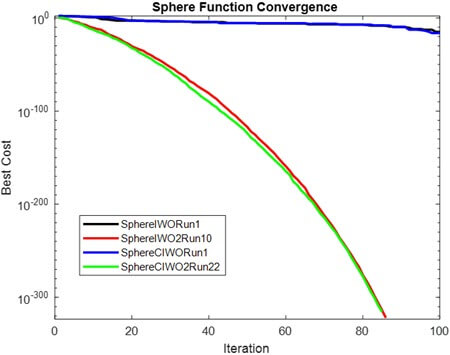
همگرایی روشهای مختلف برای مقدار بهینه تابع Sphere
در اینجا فقط یک نمونه از مقایسه و همگرایی روشهای مختلف آورده شد. ترسیم این نمودار برای همه روش ها انجام شده و در گزارش نیز آمده.
جهت اطلاع از مقادیر عددی هر تابع برای روش های مختلف به صورت زیر داریم:
جدول 5) نتایج کمینه سازی تابع Rastrigin با 30 اجرا توسط الگوریتمهای IWO مختلف
| عملکرد | IWO ساده | IWO بهبود یافته | IWO آشوب | IWO آشوب بهبود یافته |
| میانگین هزینه ها | 0223/0 | 118/0 | 0958/0 | 0797/0 |
| بهترین هزینه ها | 10-14×17/8 | 0 | 0 | 0 |
| بدترین هزینه ها | 5083/177 | 2355/111 | 70/86 | 6520/165 |
جدول 7) نتایج کمینه سازی تابع Griewank با 30 اجرا توسط الگوریتمهای IWO مختلف
| عملکرد | IWO ساده | IWO بهبود یافته | IWO آشوب | IWO آشوب بهبود یافته |
| میانگین هزینه ها | 10-4×85/7 | 10-6×85/8 | 10-4×54/2 | 10-5×61/3 |
| بهترین هزینه ها | 10-16×33/3 | 0 | 0 | 0 |
| بدترین هزینه ها | 4684/0 | 3098/0 | 2745/0 | 4944/0 |
جدول 9) نتایج کمینه سازی تابع EF10 با 30 اجرا توسط الگوریتمهای IWO مختلف
| عملکرد | IWO ساده | IWO بهبود یافته | IWO آشوب | IWO آشوب بهبود یافته |
| میانگین هزینه ها | 10-4×94/6 | 10-۵×۲۳/۵ | ۱۰-۵×۸۵/۶ | 10-۶×۰۲/۵ |
| بهترین هزینه ها | 10-7×86/9 | ۰ | 10-۷×۶۶/۴ | ۰ |
| بدترین هزینه ها | 0276/0 | ۰۲۱۳/۰ | ۰۲۷۵/۰ | ۰۲۱۸/0 |
جدول 11) نتایج کمینه سازی تابع EASOM با 30 اجرا توسط الگوریتمهای IWO مختلف
| عملکرد | IWO ساده | IWO بهبود یافته | IWO آشوب | IWO آشوب بهبود یافته |
| میانگین هزینه ها | 8579/2- | 8869/2- | 8620/2- | 8869/2- |
| بهترین هزینه ها | 9910/2- | 9911/2- | 9910/2- | 9911/2- |
| بدترین هزینه ها | 10-12×50/3- | 10-7×48/1- | 10-8×13/8- | 10-7×48/1- |
جدول 13) نتایج بدست آمده از بهترین مقدار تابع هزینه و تنظیم پارامترهای کنترلکننده PID توسط الگوریتمهای IWO مختلف
| عملکرد | IWO ساده | IWO بهبود یافته | IWO آشوب | IWO آشوب بهبود یافته |
| مقدار تابع هدف | 96/14 | 35/14 | 29/13 | 28/13 |
| Kp | 06/35 | 71/32 | 92/46 | 68/47 |
| Ki | 52/98 | 20/84 | 100 | 81/99 |
| Kd | 35/9 | 94/1 | 73/2 | 76/2 |
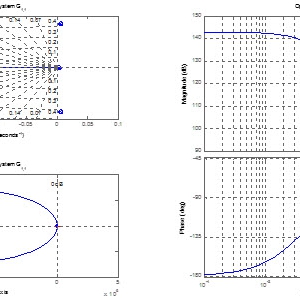
جدول 14) نتایج مشخصههای پاسخ پله بدست آمده توسط الگوریتمهای IWO مختلف
| عملکرد | IWO ساده | IWO بهبود یافته | IWO آشوب | IWO آشوب بهبود یافته |
| میانگین مربعات خطا | 029/0 | 0059/0 | 0046/0 | 0045/0 |
| زمان نشست | 0.382 | 1453/0 | 1049/0 | 1034/0 |
| زمان صعود | 198/0 | 0919/0 | 0660/0 | 0651/0 |
| فراجهش (اورشوت) | 0 | 0408/0 | 0 | 0 |
میتوان مشاهده نمود که سریعترین پاسخ توسط CIWO2 بدست آمده است. پس بازده این روش در تنظیم پارامتر بهینه کنترلکننده PID تایید میشود.
شبیه سازی در محیط متلب 2020a انجام و اجرا شده است.
نتیجه گیری و پیشنهاد:
نتایج شبیهسازی الگوریتمهای IWO ساده، بهبودیافته، آشوب، و آشوب بهبود یافته برای حل مسائل کمینه سازی توابع معیار و تنظیم پارامترهای کنترلکننده PID نشان دادند که تئوری آشوب و رابطه جدید بهبود الگوریتم میتوانند سرعت همگرایی الگوریتم را بیشتر کنند. بنابراین، اثربخشی روش IWO آشوب بهبود یافته تأیید میشود.
[1] A. R. Mehrabian, C. Lucas, 2006. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inf. 1 (4), 355–366.
[2] M. Misaghi, M Yaghoobi, 2019. Improved invasive weed optimization algorithm (IWO) based on chaos theory for optimal design of PID controller, Journal of Computational Design and Engineering. 6(3), 284-295.
کلیدواژه:
شبیه سازی الگوریتم بهینه سازی علفهای هرز مهاجم بهبود یافته بر اساس تئوری آشوب برای طراحی کنترلکننده PID بهینه
طبق توضیحات فوق توسط کارشناسان سایت متلبی تهیه شده است و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،.
با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.






دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.