توضیحات
Auto-tuned, Discrete PID Controller for DC-DC Converter for fast transient response
ترجمه فارسی موضوع مقاله: تنظیم خوکار, کنترل کننده PID گسسته برای مبدل dc-dc برای پاسخ سریع گذرا
طراحی کنترل کننده PIDزمان گسسته خود تنظیم برای بهبود سرعت پاسخ مبدل DC-DC
- چکیده :
عملکرد کنترل کننده های PID تنظیم شده با روش Ziegler-Nichols بطور معمول برای کاربرد های نیازمند کنترل کننده های بسیار دقیق مناسب نمی باشند.
در این مقاله یک کنترل کننده خود تنظیم پیشرفته برای یک مبدل DC-DC با تغییرات بار بزرگ به منظور دستیابی به زمان گذار کوتاه و سرعت بالا طراحی می شود.
الگوریتم شرح داده شده در این مقاله برای طراحی و تنظیم PID کنترلر زمان گسسته، به نحوی است تا پارامتر های آن با حداقل پیچیدگی در محاسبات بدست آیند.
برای بهبود پاسخ حالت گذار و زمان صعود مبدل ، پارامتر های کنترلر بطور متوالی توسط پروسس در حال تغییر و تنظیم می باشند.
در پیاده سازی این مقاله یک مبدل DC buck با المانهای غیر خطی در نرم افزار MATLAB طراحی و شبیه سازی شده است.
همچنین اثرات غیر خطی نظیر S/H ، کوانتیزاسیون ، تاخیر و اشباع در مدل حلقه بسته در نظر گرفته شده اند.
نتایج بدست آمده اثر بخشی الگوریتم مورد استفاده را در بهبود پارامتر های مورد نظر بیان خواهند ساخت.
- معرفی
مبدل های سوئیچینگ DC-DC سیستم هایی مبتنی بر الکترونیک قدرت هستند که توسط عملیات سوئیچینگ، یک سطح از ولتاژ را به سطح دیگر تبدیل می نمایند.
این ادوات به دلیل عملکرد خوب، اثر بخشی زیاد و سایز کوچک بسیار رایج و مشهور می باشند و بنابراین بصورت وسیعی در کامپیوتر های شخصی، مخابرات، مهندسی پزشکی و آداپتور های وسایل الکترونیکی استفاده می شوند.
این گستردگی استفاده مهندسین و طراحان را بر این وا می دارد تا عملکرد این مبدل ها را برای استفاده های گوناگون بهبود بخشند. مبدل های سوئیچینگ در حالت کلی سیستم های دینامیک غیر خطی متغیر با زمان می باشند.
اصولا غیر خطی بودن این سیستم ها ناشی از سوئیچینگ، ادوات الکترونیک قدرت و المان های Passive آنها نظیر سلف ها و خازن ها می باشد.
بنابراین تکنیک های سنتی کنترل خطی را نمی توان برای آنالیز و کنترل این تجهیزات بکار برد.
برای طراحی جبرانساز فیدبک در کنترل خطی یک مدل دینامیک از مبدل سوئیچینگ مورد نیاز است که این مد باید رفتار فرکانس پایین سیستم را مدل نماید ولی از رفتار سیستم در فرکانس های ناچیز و همچنین رفتار آن در فرکانس های بالاتر از فرکانس سوئیچینگ صرفنظر نماید.
بنابر این مدل کردن سیستم باعث وقوع تقریب در سیستم خواهد شد.
عملیات سوئیچینگ به صورت ذاتی موجب این می شود که ادوات مدار با یکدیگر بصورت پریودیک ارتباط داشته باشند این امر موجب تغییرات در پیکره بندی مدار در هر سیکل سوئیچینگ خواهد شد.
هر نوع از این پیکره بندی ها با مجموعه ای از معادلات حالت خطی مدلسازی می شود.
بنابراین برای آنالیز حالت گذار و طراحی کنترلر بایستی تعداد بسیار زیادی از معادلات حل شوند که این امر بسیار مشکل می باشد.
در اینجاست که تکنیک میانگین گیری باعث ساده تر شدن مساله می شود بدین صورت که برای مجموعه از سیکل های کاری یک معادله تقریبی برای سیستم ارائه می نماید.
بدین منظور به عنوان مثال می توان از یک فیلتر L-C برای صرفنظر کردن از فرکانس های بوجود آمده در سوئیچ استفاده نمود.
در شبیه سازی سیستم در MATLAB استفاده از مدل بدست آمده توسط این تکنیک نتایجی بسیار سریعتر و ساده تری در اختیار خواهد گذاشت.
امروزه با وجود پیشرفت های بسیار زیادی که در زمینه process control بدست آمده است.
هنوز کنترل کننده های PID در کنترل لوپ های بسته بسیار مشهور و پرکاربرد می باشند.
بطوریکه 97 درصد کنترل کننده های صنعتی از این ساختار استفاده می نمایند که این امر به دلیل سادگی ، عملکرد خوب و سادگی در پیاده سازی آن می باشد.
اگر روش های متعددی برای تنظیم این کنترلگر ها تا کنون معرفی شده است ولی اکثر این روش ها عملکرد کنترلر برای یکی از پارامترهای کنترلی ضعیف می باشد. تنظیم توسط روش ساده ZN یک روش معمولترین و مشهورترین روش های تنظیم کنترل کننده های PID می باشد.
به دلیل ساده بودن و مشهور بودن این روش یک روش مناسب برای کنترلگر های مرتبه اول شناخته می شود.
اما در تنظیم پارامترهای کنترلگر های مرتبه بالاتر و نیز کنترلگر های غیر خطی این روش کاربرد خود را از دست می دهد و موجب بوجود آمدن Overshoot زیاد در سیستم یا موارد نامطلوب دیگر می شود.
به منظور غلبه بر این موارد روش های متعددی برای تنظیم کنترلگر ارائه شده که برای سیستم های خطی حیاتی می باشند.
امروزه خود تنظیم بودن (Auto tuning) یک ویژگی دلخواه و مورد نیاز برای کنترل سیستم های غیر خطی می باشد.
در یک کانورتور با کنترلگر دیجیتال یک مزیت کلیدی آن است که قابلیت تنظیم خودکار پارامترها به منظور دستیابی به سطح مطلوب وجود دارد.
عملکرد و بازده خوب، مقاوم بودن ، پایداری و پیاده سازی ساده یک کنترل دیجیتال با قابلیت تنظیم خودکار می تواند یک پیشرت قابل توجه در کنترل دیجیتال د حوزه الکترونیک قدرت باشد.
یک کنترلر خود تنظیم در ابتدا بایستی دو ویژگی زیر را فراهم سازد:
- اول اینکه نبایستی اثری روی عملکرد مبدل در شرایط نامی داشته باشد.
- بایستی بر اساس الگوریتمی ساده و مقاوی باشد تا پیچیدگی محاسبات در آن به طرز قابل توجه افزایش نیابد و در پیاده سازی مدار آن مشکلی بوجود نیاورد.
از آنجا که رگولاتور های PID به طور گسترده ای در میکروکنترلر ها ، FPGA و DSP کاربرد دارند امروزه این کنترلگر ها جایگاه خود را در کاربردهای الکترونیک صنعتی نیز پیدا کرده اند.
استخدام برنامه نویس متلب در سایت متلبی
در مراجع [5] و [18] مقاله مربوطه، نتایج بدست آمده از یک مبدل DC-DC با کنترلگر PID تنظیم شده با روش Ziegler-Nichols جهت بهبود سرعت پاسخ حالت گذار با تغییرات بار و set point آورده شده است.
در این مقاله یک کنترلگر PID نوعی مطرح شده در مراجع [5] و[18] برای یک میدل dc-dc تطبیق داده شده است که در آن ضرایب گین های مشتق گیر، انتگرالگیر و گین تناسبی به صورت پیوسته با توجه به پروسه کنترل در حال تنظیم و تغییر می باشند.
در این مقاله اثرات این کنترلگر در بهبود شرایط این مبدل بررسی خواهد شد.
- طراحی Buck Convertor
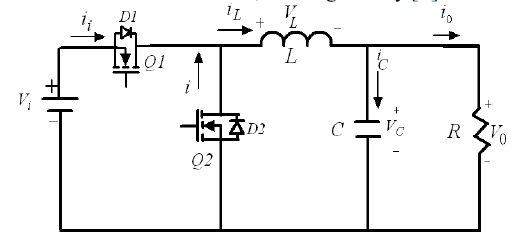
برای مبدل Buck نشان داده شده در شکل 1 ، رابطه بین ولتاژ خروجی (Vo) و ولتاژ ورودی (Vi) بصورت زیر است :
شکل1- طبقه قدرت یک مبدل Buck DC-DC
که در این رابطه بوده و دوره زمانی سوئیچینگ و زمان روشن بودن سوئیچ می باشد.
شرایط مرزی CCM و DCM مقدار مرزی L را طبق رابطه ذیل بیان می کند:
…
که در این رابطه R مقاومت بار و فرکانس سوئیچینگ می باشد. مقدار اندوکتانس سلفی می بایستی بیشتر از باشد.
در حالت کلی ریپل مجاز برای طراحی تا 30درصد میانگین خروجی جریان در نظر گرفته می شود[19],[20].
بنابر این طراحی صحیح و قابل قبول مقدار L را از رابطه زیر بدست آورد:
…
مقدار اولیه C با استفاده از رنج مجاز برای تعیین می شود که معمولا برابر با 2% ولتاژ خروجی در نظر گرفته می شود.
ریپل کلی ولتاژ خروجی ناشی از دو مساله ESR خازن خروجی و شارژ و دشارژ این خازن می باشد.
و طبق [20] از رابطه زیر بدست می آید:
…
مقدار خازن مورد استفاده به عواملی نظیر تغییرات بار، سرعت حلقه و میزان سلف بستگی داشته و طبق رابطه زیر بدست می آید:
…
که در این رابطه و جریان های خروجی تحت بار های زیاد و کم و و به ترتیب ولتاژهای پیک نهایی و اولیه خازن می باشند.
برای طراحی کانورتور پارامترهای زیر را در نظر می گیریم
R=1~2Ω I0=1.25amp ,
output ripple of 25 mV , output load response of 0.25 , , ,
, of , fs=195KHz , L=10μH , C=47μf
- مدلسازی کانورتور DC-DC در MATLAB
بعد از طراحی می توان مبدل سوئیچینگ را توسط روش های عددی و با استفاده از معادلات سیستم شبیه سازی نمود.
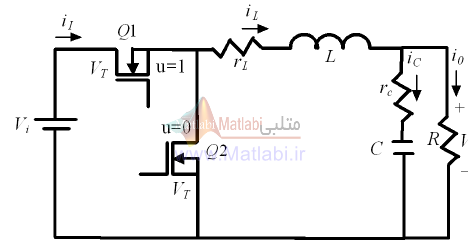
شکل 2- کانورتور باک با المان های غیر ایده آل
دینامیک های این کانورتور در CCM را میتوان با تحلیل مدار شکل2 وضعیت هدایت سوئیچ Q1 وQ2 و بدست آورد.
عملیات سوئیچینگ توسط تابع u نشان داده می شود که این تابع متواند مقادیر 0 و 1 را شامل شود.
برای حالتی که سوئیچ Q1 اکتیو است داریم و و برای اکتیو بودن سوئیچ Q2 برعکس این حالت اتفاق خواهد افتاد.
برای یک کانورتور ایده آل غیر ایزوله داریم :…
(برای زمان روشن بودن) و برای زمان خاموش بودن :…
معادلات دینامیک و نیز معادلات خروجی کانورتور باک عبارتند از :
پس از ساده سازی های ریاضی معادلات فوق معادلات دینامیک و خروجی سیستم جهت شبیه سازی در محیط سیمولینک بدست می آید.
شکل 3 و شکل 4 نشان دهنده مدل این مبدل در محیط SIMULINK می باشند :
…
شکل 3 مدل سیمولینک مبدل Buck DC-DC
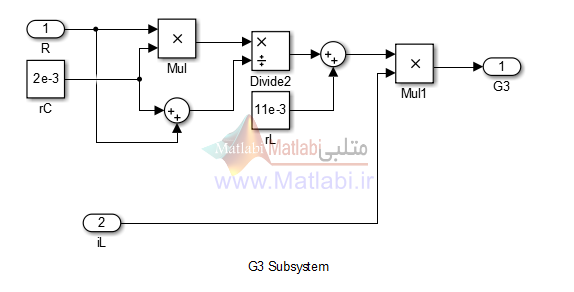

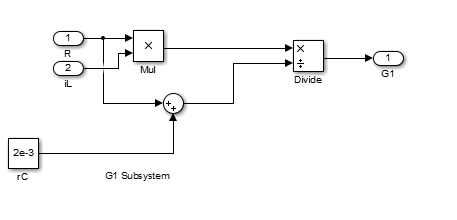
شکل 4- زیر سیستم های G1,G2,G3,G4 مربوط به مدل SIMULINK کانورتور
- سیستم کنترل حلقه بسته برای مبدل DC-DC
شکل5 شمای کلی سیستم کنترل حلقه بسته را برای یک مبدل DC-DC با فیدبک بر اساس کنترلر PID نشان می دهد.
در اینجا هدف آنست که اختلاف میان و مینیمم شود.
همانطور که در شکل 5 دیده می شود 4 عدد Function Block اصلی در این بلوک دیاگرام دیده می شود :
ADC ( تبدیل کننده آنالوگ به دیجیتال) ، COMPENSATOR (جبرانساز خطا) ، DPWM ( مدلاتور پهنای باند دیجیتال) و DC-DC CONVERTOR که مدل بدست آمده برای مبدل می باشد.
ADC سیگنال آنالوگ را نمونه برداری می کند و DPWM برای تولید سیگنال درایور بر طبق قوانین کنترلی متناظر بکار برده می شود و همچنین جبرانساز وظیفه تولید سیگنال کنترلی با جبرانسازی سیگنال خطا ( را بر عهده دارد.
شکل 5 بلوک دیاگرام یک مبدل سوئیجینک با جبرانسازPID فیدبک
خطای بین ولتاژ خروجی و ولتاژ مرجع توسط جبرانساز دارای PID پردازش می شود تا سیگنال کنترلی متناسب تولید گردد.
برای کنترل دیجیتال مبدل های سوئیچینگ dc-dc می توان توسط بلوک compensator به وجود کنترلر PID پی برد.
سیگنال کنترلی به صورت قابل ملاحظه ای روی خواص کانورتور تاثیر مسقیم خواهد داشت.
بنابراین مهم است که یک راه مناسب برای ساخت یک کنترلگر دیجیتال مناسب در نظر گرقته شود تا موجب فراهم آمدن عملکرد بهتر در مبدل dc-dc گردد.
در مبدل های dc-dc کنترلگر PID به منظور محاسبه duty cycle متناسب با میزان خطا استفاده می شود.
سیگنال خروجی کنترلر به DPWM رفته تا پالس سوئیجیگ کانورتور را تولید کند.
- الگوریتم پیاده سازی کنترلر PID زمان گسسته
به صورت کلی یک کنترلگر PID در فیدبک موجب جبرانسازی در فیدبک می شود.
معادله کلی کنترلگر PID زمان پیوسته بصورت زیر می باشد :
که در آن u(t) سیگنال خروجی (سیگنال کنترلی) ، گین تناسبی ، زمان انتگرالی یا همان زمان reset ، زمان مشتقی یا همان rate time و e سیگنال خطای بین ورودی مرجع و خروجی می باشد.
تابع تبدیل یک کنترلگر PID به صورت زیر است:
که در این رابطه : و گین های انتگرالی و مشتق گیر می باشند.
از روش معادله دیفرنس بازگشتی میتوان رابطه (14) را به حوزه زمان گسسته انتقال داد.
روابط (15) تا (17) نحوه تبدیل معادله زمان پیوسته کنترلگر را به حوزهz نشان می دهد.
شکل 6 نیز نمایشگر پیاده سازی یک کنترلگر PID زمان گسسته درMATLAB SIMULINK می باشد.
…
شکل 6 – شمای یک کنترلگر PID زمان گسسته کلی در MATLAB SIMULINK
بطور مشابه برای یک کنترلگر دیجیتال PID با زمان نمونه برداری با نوشتن معادلات مشتق گیر و انتگرالگیر به صورت معادلات دیفرنس بازگشتی معادله دیفرنس کنترل کننده به صورت زیر بدست می آید :
که در این رابطه اندیس های n و j به ثابت های زمانی اشاره می نماید.
می توان معادله کنترل کننده را بصورت زیر ساده نمود:
که در این رابطه ثابت انتگرالی دیجیتال و ثابت مشتق گیر دیجیتال و گین تناسبی دیجیتال می باشد.
برای محاسبه حاصل جمع میزان خطا ها، مقادیر تمامی خطاها در زمان های قبلی ذخیره می شود.
به این روش Positioning algorithm میگویند.
- کنترلر PID با تیونینگ اتوماتیک
بلوک دیاگرام کنترل کننده خود تنظیم PID در شکل 7 قابل مشاهده است.
همانطور که پیداست فاکتور β(k) به طور پیوسته گین های کنترل کننده را تنظیم می نماید.
این فاکتور تابعی از خطا e(k) و میزان تغییرات آن می باشد.
بنابراین نقطه شروع برای تنظیم کنترل کننده خود کنترل کننده می باشد.
پارامترهای کنترل کننده را می توان توسط هر یک از روش های استاندارد بدست آورد.
لذا در این مقاله پارامترهای اولیه کنترل کننده از روش ZN بدست آمده است.
که هر کدام از این پارامترها توسط فاکتور β(k) بصورت آنلاین در حال تنظیم می باشند.
معادله تفاضلی کنترل کننده PID را میتوان به صورت زیر بیان نمود :
که در این رابطه u(k) سیگنال کنترلی در k امین نمونه زمانی می باشد.
ضرایب ، و بر طبق سیکل تنظیم نهایی ZN محاسبه شده اند.
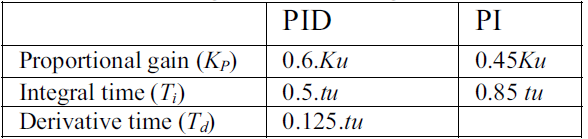
سیکل نهایی Ziegler-Nichols یا تظیم حلقه بسته کنترلر به عنوان یکی از دقیق ترین و معمول ترین روش های تنظیم کنترلر های PID و PI برای رنج وسیعی از کاردهای صنعتی شناخته می شود.
روش و پارامتر های تنظیمی Ziegler-Nichols بر اساس اطلاعات عملی برای گین نهایی و دوره نهایی در جدول 1 نشان داده شده است :
جدول1- فرمول تنظیم بر اساس قاعده Ziegler-Nichols
برای مبدل DC-DC مطرح شده در این مقاله سیگنال خطا و تغییرات خطا به صورت زیر بیان می شود
ضریب تنظیم پارمترها β(k) نیز به صورت زیر در نظر گرفته می شود :
در اینجا و مقادیر نرمالیزه شده خطا و تغییرات خطا می باشند.
از معادله (23) میتوان در نظر گرفت که ضریب تغییرات β مقداری در بازه [-1,1] می باشد.
در این روش گین های تناسبی، مشتق گیر و انتگرال گیر توسط این ضریب به صورت پیوسته در حال تنظیم شدن می باشند.
تنظیم این ضرایب برطبق معادلات تجربی زیر در نظر گرفته می شوند :
با استفاده از معادله (14) تابع تبدیل کنترلر PID با تنظیم اتوماتیک بصورت زیر خواهد شد :
با استفاده از معادله(15) تابع تبدیل کنترلر در حوزه Z بدین صورت خواهد شد:
بصورت مشابه برای کنترلر PID دیجیتال با زمان نمونه برداری Ts معادله تفاضلی برابر است با :
که در این معادله ، و ضرایب تنظیم شده تناسبی ، انتگرال گیر و مشتق گیر در k امین نمونه زمانی بوده و سیگنال کنترلی متناظر در آن نمونه می باشد.
K1 ، K2 و K3 سه ثابت مثبت می باشند که برای ساختن ، و از مقادیر اولیه متناظر استفاده شده اند تا جواب مورد نظر بدست آید.
این پارامترها بصورت پیوسته با انتخاب مقادیر مناسب K1، K2 و K3 در حال تنظیم می باشند.
انجام پروژه متلب را به متلبی بسپارید.
در اینجا هدف این است که با هر تغییر منبع ولتاژ و یا تغییرات و نوسانات بار ، ضرایب ، و توسط عامل غیر خطی β بصورت پیوسته به گونه ای تنظیم شوند تا مبدل با سرعت قابل قبولی به شرایط کاری عادی بازگردد و نیز تناوب در آن زیاد نباشد.
معادلات (24) و (25) نشان می دهد که و در طول سیکل کاری در حال افزایش هستند هر چند که میزان افزایش آنها به دلیل یکسان نبودن ضرایب K1 و K3 یکسان نخواهد بود.
این در حالی است که ضریب انتگرالی بسته به علامت خطا ممکن است زیاد یا کم شود.
یک ویژگی مهم این کنترلر آن است که ساختاری بسیار شبیه با ساختار کنترلر های PID سنتی داشته و یک PID معمولی را به این روش می توان با اعمال عامل β به یک کنترل کننده خودتنظیم تبدیل نمود.
همچنین مدل ارائه شده یک مدل ناوابسته می باشد زیرا عامل β تنها به شرایط اخیر پورسس، خطای نرمالیزه شده و تغییرات نرمالیزه شده خطا بستگی دارد.
- پیاده سازی کنترلر PID زمان گسسته با تنظیم اتوماتیک برای یک Buck Converter
مقادیر اولیه کنترلر با استفاده از روش Ziegler-Nichols تنظیم شده است.
در تنظیم این پارامترها معیار پایداری به نسبت پاسخ پله دارای اهمیت بیشتری بوده است.
بصورت خلاصه روش تجربی تنظیم عملی به شرح زیر است:
- کنترلر را در مد تناسبی قرار دهید
- KP را به عنوان متغیر در نظر بگیرید Ti برابر بینهایت و Td صفر در نظر گرفته می شود.
- Kd از صفر تا نقطه بحرانی افزایش داده می شود به عنوان مثال تا حدی که سیستم در شرایط پایداری مرزی قرار گیرد.
- در این شرایط Kd ثبت می شود این مقدار برابر با گین نهایی یا Ku خواهد بود و زمان متناسب با این شرایط دوره نهایی tu می باشد.
- از جدول 1 فرمول های روش Ziegler-Nichols بر حسب مقادیر تجربی Ku و tu مشخص می باشد.
- این مقادیر برای بدست آوردن مقادیر مورد نیاز برای تنظیم پارامتر ها استفاده می شود.
مقادیر بدست آمده از روش فوق پارامترهای اولیه کنترلر می باشد.
با سعی و خطا می توان مقادیر نهایی گین های تناسبی ، مشتق گیر و انتگرال گیر را بدست آورد.
در شکل 6 ساختار کنترلر PID با پارامتر های تنظیم شده قابل مشاهده می باشد.
برای بدست آوردن تبدیل z تابع تبدیل کنترلر PID خود تنظیم با معادله (28) روابط تجربی زیر استفاده می شوند :
با استفاده و جایگذاری پارامتر های تنظیم شده معادلات تجربی کنترلر برای اعمال روی مبدل Buck به شرح زیر می باشد :
مدل پیاده شده در MATLAB SIMULINK برای کنترلر PID خود تنظیم دیجیتال در شکل 7 قابل مشاهده است.
همچنین پارامترهای تنظیم شده کنترلر در شکل 8 نشان داده شده است.
….
شکل 7- ساختار کنترلر PID زمان گسسته خود تنظیم برای DC-DC Convertor
…
شکل 8- گین های تنظیم شده تناسبی، مشتق گیر و انتگرال گیر در سیمولینک
همانطور که ذکر شد مقادیر دقیق پارامتر های تنظیم شده کنترلر از معادلات (33)، (34) و (35) بدست می آید.
- نتایج شبیه سازی با متلب
تا اینجا مدل مبدل و مدل کنترل کننده برای شبیه سازی و پیاده سازی در MATLAB SIMULINK طراحی شد.
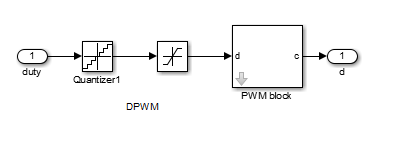
برای راه اندازی موتور نیاز به یک مدولاتور PWM دیجیتال یا DPWM می باشد که سیگنال پالسی متناظر با Duty cycle برای کنترل کننده تولید می کند و دارای رزولوشن 9 بیتی می باشد.
این بلاک شامل قسمت های کوانتیزر ، محدود کننده ضریب سیکل کاری و بلوک گین می باشد.
شکل 9 مدل ارائه شده برای شبیه سازی این قسمت را نشان می دهد.
شکل9- مدل شبیه سازی شده برای DPWM
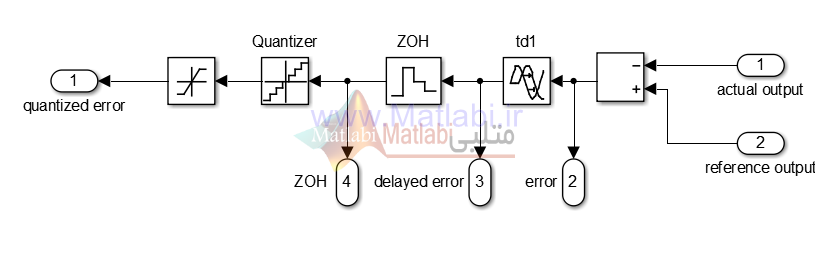
همچنین بلوک A/D Convertor به گونه ای طراحی شده است تا اختلاف ولتاژ خروجی و ولتاژ مرجع را همواره محاسبه کرده و آن را به صورت زمان گسسته با عنوان خطای کوانتیزه شده تحویل می دهد.
در این بلوک اثرات اشباع و تاخیر زمانی نیز در نظر گرفته شده است.
شکل 10 نشان دهنده مدل شبیه سازی شده برای این بلوک در سیمولینک می باشد.
در اینجا طراحی به گونه ای صورت گرفته است تا علاوه بر خطای کوانتیزه شده بتوان خطای با تاخیر (delayed error) خطای آنالوگ (error) و خطای دیجیتال شده توسط ZOH را مشاهده نمود.
شکل 10- مدل شبیه سازی شده برای ADC در MATLAB SIMULINK
در شکل 11 شبیه سازی مدار کنترل ولتاژ خروجی توسط یک کنترلر PID خود تنظیم برای یک مبدل Buck DC-DC در محیط SIMULINK را نشان می دهد.
در این شبیه سازی و تغییرات بار بین 1 تا 2 اهم می باشد.
….
شکل11- مدل یک مبدل باک با کنترل کننده PID دیجیتال خود تنظیم در SIMULINK
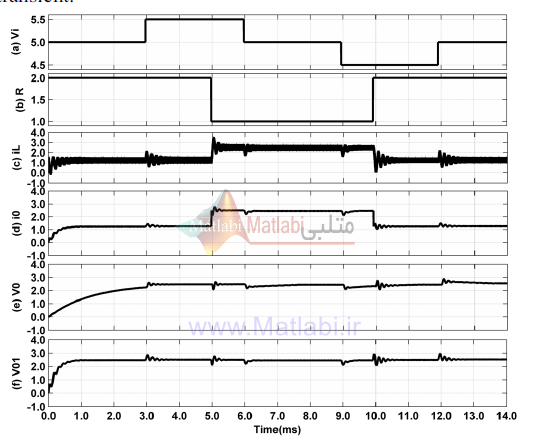
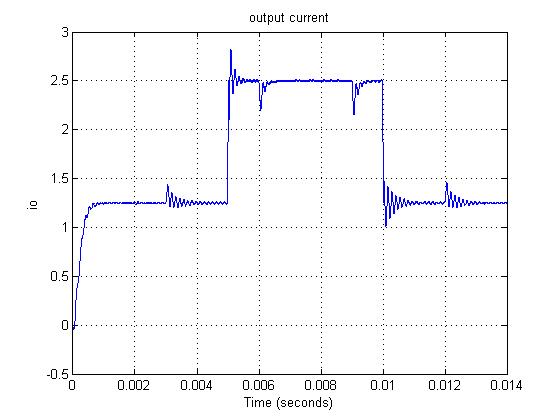
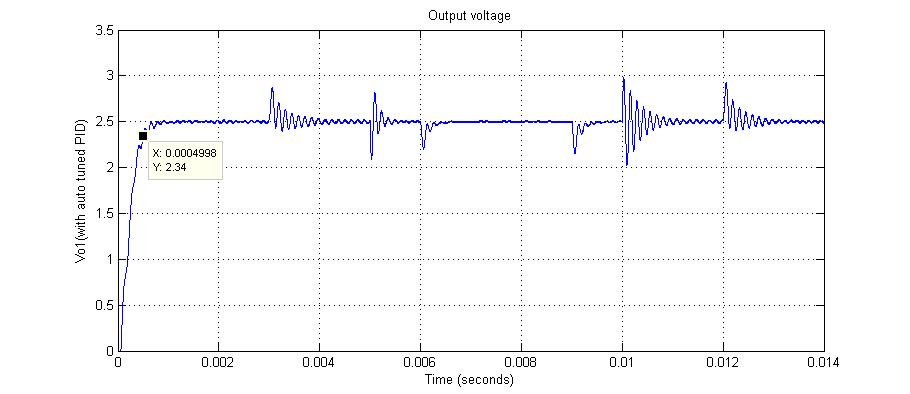
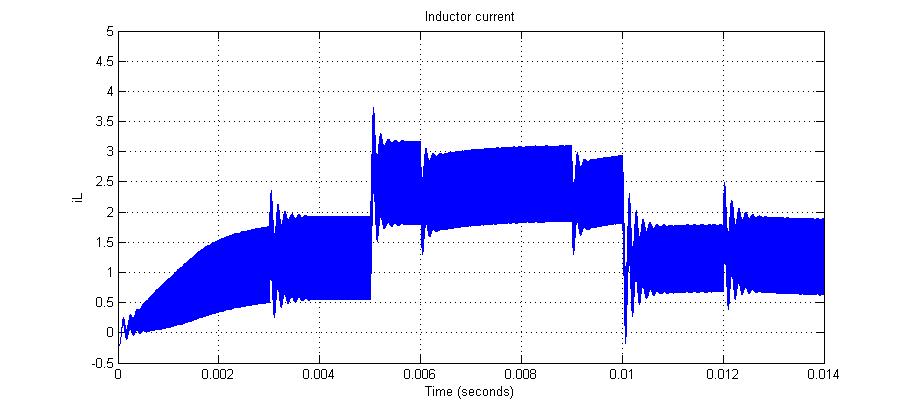
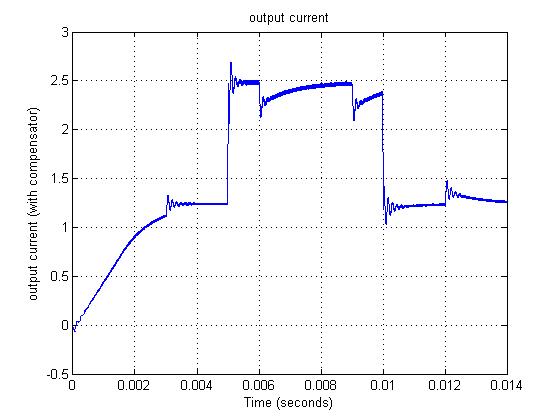
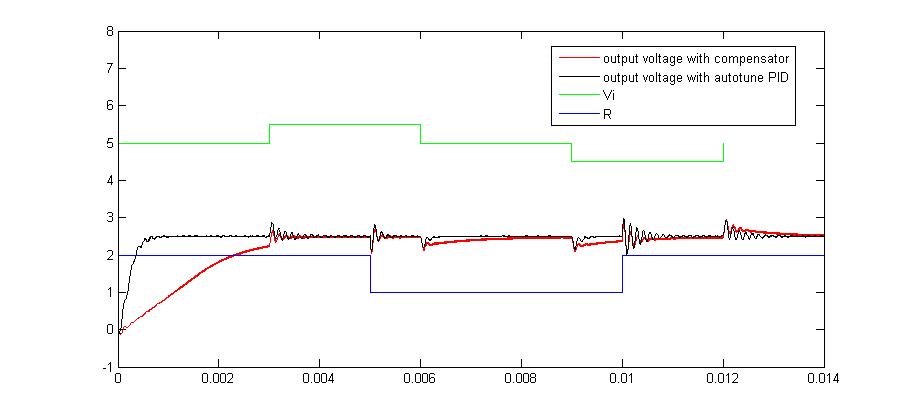
نتایج شبیه سازی برای جریان خروجی io ، جریان سلف iL ، ولتاژ خروجی Vo1 (در حضور PID خود تنظیم) و ولتاژ خروجی Vo ( با PID) در شکل 12 آورده شده است.
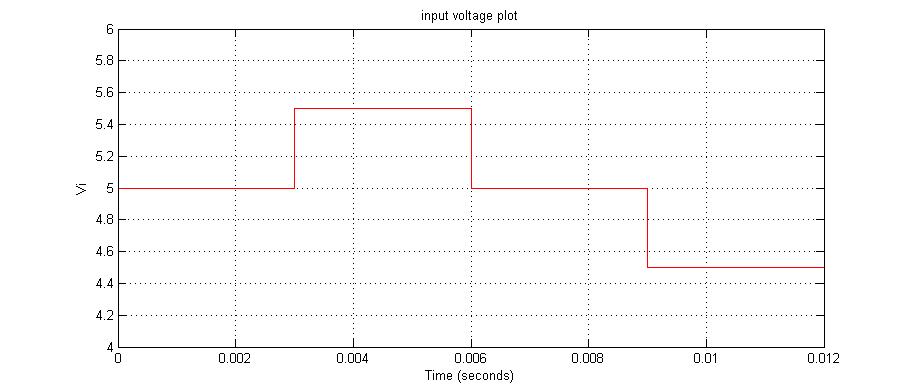
نمودار اول نمایشگر ولتاژ ورودی به کانورتور می باشد که بین مقادیر 4.5 5 5.5 نوسان میکند .
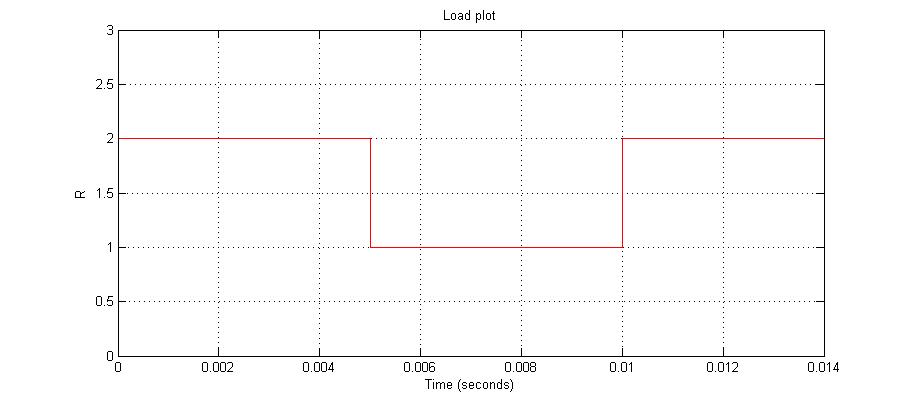
نمودار دوم نشان دهنده تغییرات بار می باشد که بین مقادیر 1-2 اهم با دوره زمانی 10 میلی ثانیه نوسان می نماید.
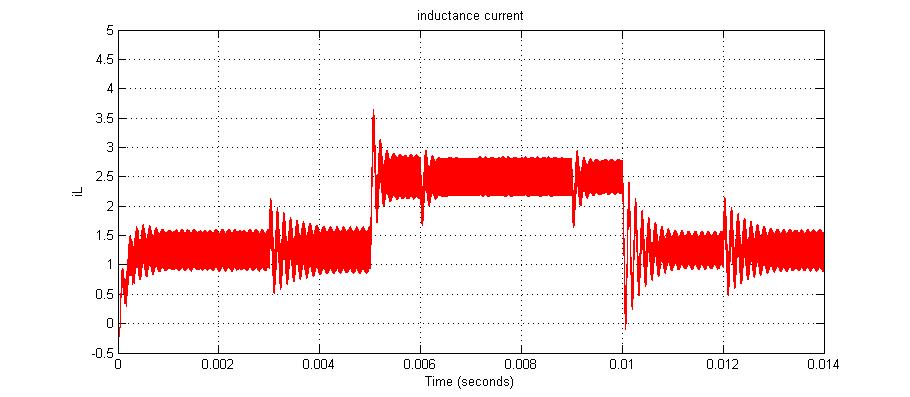
شکل سوم جریان سلف را نشان می دهد واضح است که متوسط این جریان با تغییر بار تغییر خواهد کرد.
جریان خروجی در شکل چهارم قابل مشاهده می باشد.
ملاحظه می شود که این مقدار با تغییر بار بین 1.5 تا 2.5 تغییر می کند همچنین تغییرات ولتاژ ورودی در آن موجب بالازدگی و نوسان می گردد.
تغییرات ولتاژ خروجی کانورتور در نمودار پنجم مشاهده میگردد.
همانطور که در شکل مشخص است زمان صعود برابر با 0.5 msec است که هدف طراحی را برآورده می سازد.
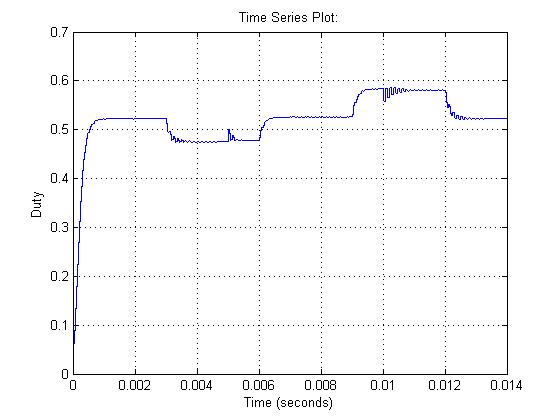
شکل 12- a) ولتاژ ورودی b) تغییرات بارc)جریان سلف d) جریان خروجی e) ولتاژ خروجی d) سیکل وظیفه
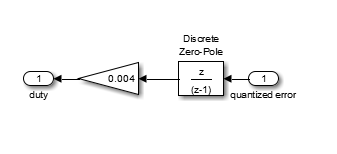
( این کار در مقاله اصلی انجام نشده و تنها به مرجعی دیگر رجوع داده شده است ولی در اینجا بمنظور درک بهتر عملکرد کنترل کننده طراحی شده این مطلب اضافه گردیده است ) شکل زیر نشان دهنده ساختار این جبرانساز می باشد.
فایل سیمولینک مربوطه با عنوان Buck convertor controlling by compensator ضمیمه شده است.
شکل 13- جبرانساز طراحی شده برای کانورتور باک
نتایج بدست آمده از شبیه سازی، در شکل های زیر قابل مشاهده می باشد.
…
شکل 14- ساختار پیاده شده برای کنترل کانورتور باک با یک جبرانساز PI
شکل 15- a)ولتاژ خروجی در حضور جبرانسازb) جریان القاگر در حضور جبرانسازc) جریان خروجی در حضور جبرانساز
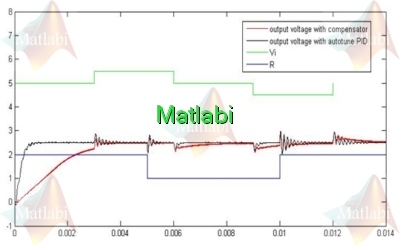
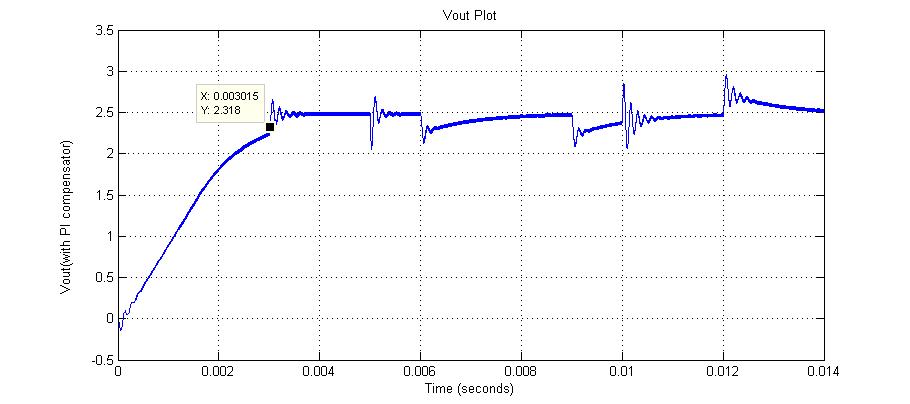
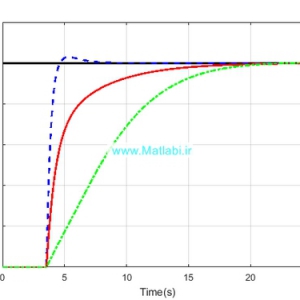
در شکل 16 ولتاژ خروجی حاصل از دو روش کنترل با جبرانساز PI و کنترل با کنترلر PID خود تنظیم مقایسه شده است.
با توجه به شکل می توان دید که زمان صعود برای حالت کنترلر خود تنظیم برابر با 0.5 msec بوده در حالی که این زمان برای حالت کنترل با جبرانساز برابر با 3 msec می باشد.
لذا هدف طراحی که رسیدن به پاسخ سریعتر بود در اینجا محقق شده است.
شکل 16 مقایسه نتایج دو روش برای ولتاژ خروجی
شکل 17- نتایج بدست آمده درمقاله اصلی
جدول 2 مشخصات پاسخ را برای حالت استفاده از کنترلر PID خود تنظیم نشان می دهد.
این جدول با بررسی شکل 16 برای دو پاسخ بدست آمده است.
دقت شود مقادیر بدست آمده در این جدول نسبت به مقادیر مقاله اصلی دارای کمی اختلاف می باشد.
که این امر ممکن است ناشی از تفاوت در بلوک های DPWM و یا ADC و یا گین های استفاده شده در سیستم باشد که در مقاله اصلی ساختار و مقدار آنها مشخص نبوده و طراحی آن بر اساس مراجع مذکور در مقاله انجام شده است.
لیکن در حالت کلی نتایج بدست آمده در شبیه سازی شباهت بسیار زیادی با نتایج مقاله اصلی دارد.
| Performance parameters | Type of Transient | % | Compensator | Auto tuned PID |
| Transient response | Input transient | Overshoot | 6 | 13 |
| Undershoot | 16 | 12.5 | ||
| Load transient | Overshoot | 14 | 16 | |
| Undershoot | 17 | 17 | ||
| Rise time(ms) | — | 3 | 0.5 | |
| Settling time (ms) after |
Input transient | — | 0.8 | 0.3 |
| Load transient | — | 0.5 | 0.35 |
جدول 2 مشخصات ولتاژ خروجی بدست آمده
طبق جدول 2 زمان صعود با طراحی کنترلر PID خود تنظیم برای کنترل ولتاژ خروجی از 3 میلی ثانیه در حالت جبرانساز PI و 2.5 میلی ثانیه در PID در مقاله اصلی به 0.5 میلی ثانیه کاهش یافته است.
همچنین زمان نشست از 0.8 میلی ثانیه (در تغییرات ولتاژ ورودی) و 0.5 (در تغییرات بار) در حالت جبرانساز و کنترلر PID معمولی به 0.3 و 0.35 میلی ثانیه در حالت کنترلر PID خود تنظیم کاهش یافته است.
- نتیجه
در این مقاله یک مدل ساده از یک کنترل کننده دیجیتال با تنظیم اتوماتیک برای یک Buck DC-DC Converter به منظور بهبود بخشی به سرعت پاسخ حالت گذار سیستم طراحی گردید.
در این سیستم گین های کنترلر به صورت پیوسته و داخلی توسط عامل غیر خطی β که بستگی به شرایط پروسس و خطای سیستم بستگی دارد تنظیم می شود.
ساختار ارائه شده را می توان به هر کنترلر PID معمولی دیگر نیز اعمال نمود.
کارایی این کنترلر توسط شبیه سازی سیستم در SIMULINK بررسی گردید.
در این بررسی کارایی کنترلر طراحی شده با یک کنترلر PID معمولی و یک جبرانساز PI مقایسه گردید.
در این بررسی ها کنترلر دیجیتال خود تنظیم هم در شرایط گذرا و هم در حالت ماندگار از خود عملکرد بهتری نشان داد.
همچنین این کنترلر را از آنجایی که تنها به میزان خطای نرمالیزه شده و تغییرات آن وابسته است می توان یک کنترل مستقل و نابسته به سیستم معرفی نمود.
کلید واژه: DC-DC Converter, PID Controller, Autotuned PID controller, modeling and simulation
شبیه سازی مقاله Auto-tuned, Discrete PID Controller for DC-DC Converter for fast transient response
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

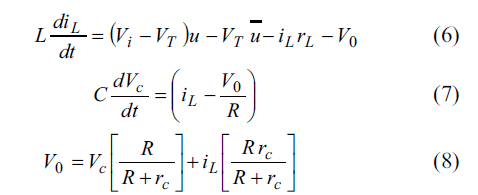
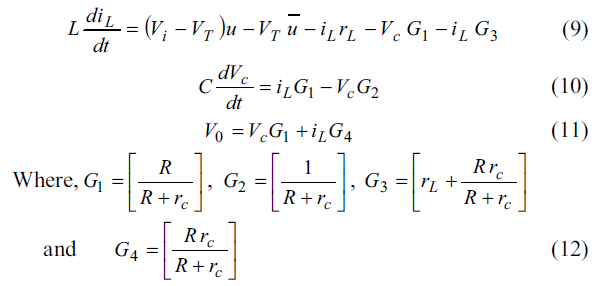
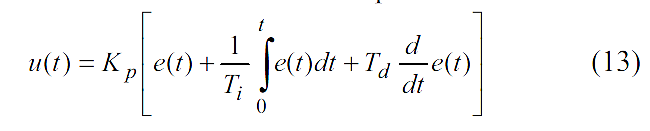
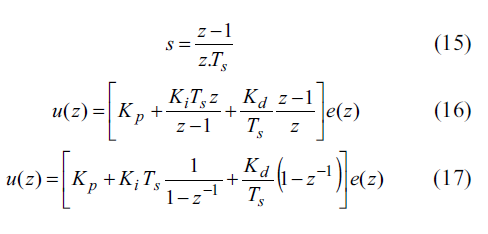
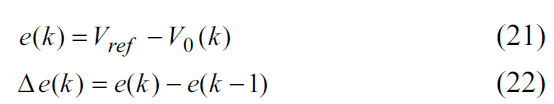
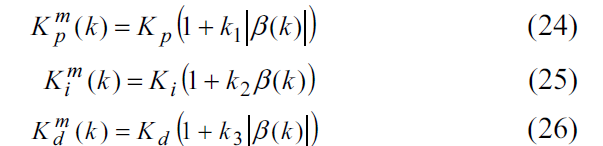
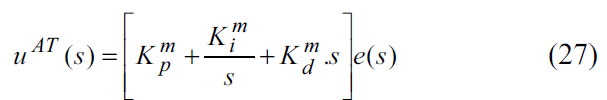
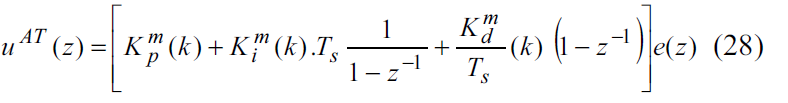
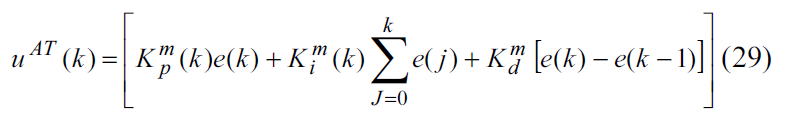
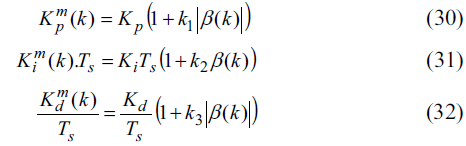
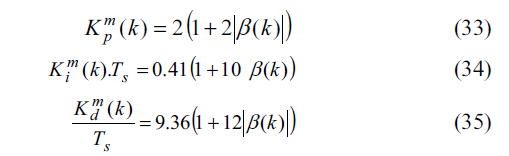




دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.