توضیحات
Least squares based and gradient based iterative identification for Wiener nonlinear systems
ترجمه فارسی موضوع مقاله: شناسایی تکراری مبتنی بر حداقل مربعات و گرادیانی برای سیستم های غیر خطی وینر
مقدمه:
مدلهای غیر خطی مانند سیستمهای وینر و همرشتاین برای تقریب بسیاری از فرآیندهای دینامیکی غیر خطی مورد استفاده قرار میگیرند.
یک سیستم وینر از یک بلوک دینامیکی خطی و یک بلوک غیر خطی استاتیک تشکیل میشود.
در این پروژه بر اساس کارهای تا به حال انجام شده، یک روش گرادیان نزولی تکراری و یک روش کمترین مریعات تکراری برای شناسایی سیستمهای وینر ارائه میشود.
برای این کار یک تابع هزینه تعریف میشود و از اصول شناسایی سلسله مراتبی برای مینیمم سازی آن استفاده میشود.
تعریف مساله:…
سیستم وینر زیر را یا نویز رنگی در نظر بگیرید:…
که در آن u و y ورودی و خروجی سیستم، v یک نویز سفید با متوسط صفر، و توابع معلوم غیر خطی هستند. با تعریف:
معادله (1) به صورت زیر قابل بازنویسی است:…
فرض کنید:…
تقریبهایی از و در تکرار k باشند. اگر L طول دادهها باشد، با فرض
تابع هزینه به صورت زیر تعریف میشود:…
تابع هزینه بالا را به روش کمترین مربعات تکراری بهینه سازی میکنیم.
روش کمترین مربعات تکراری
تعاریف زیر را در نظر بگیرید:
در معادلات بالا متغیرهای دارای علامت نشان دهنده تقریب متغیر مربوطه توسط الگوریتم است.
با دقت در رابطه (16) میبینیم که مقادیر نویز در زمانهای مختلف در اختیار نیست.
بنابراین باید تخمین آن را در الگوریتم به کار ببریم. این کار در هر تکرار با رابطه زیر انجام میشود:…
با استفاده از تعاریف بالا رابطة تخمین پارامترها در تکرار k به صورت زیر میباشد:…
برای این الگوریتم موارد زیر را در نظر میگیریم:…
- مقدار اولیه پارامترها یعنی را غیر صفر و تصادفی و به نحوی تعیین میشود که و همچنین به صورت تصادفی تعیین میشود.
- بعد از به روز کردن پارامترها قرار میدهیم:…
- در هر مرحله بعد از به روز رسانی آنرا با رابطة زیر نرمالیزه میکنیم:…
- شرط توقف الگوریتم را رسیدن نرم بردار اختلاف با به مقداری کوچک (مثل ) قرار میدهیم.
روش گرادیان نزولی تکراری
این روش مشابه روش قبل است، فقط در آن تغییرات زیر را انجام میدهیم:…
- بعد از محاسبه در الگوریتم، پارامترهای زیر تعیین میشوند:…
- بعد از محاسبه نرخهای آموزش بالا، پارامترهای مدل توسط روابط زیر به روز میگردد:…
مثال شبیه سازیها
در شبیه سازیهای این دو الگوریتم سیستم وینر زیر را در نظر میگیریم:…
همچنین ورودی u(t) به صورت نویز سفید با متوسط صفر و واریانس 1 که برای پایداری سیستم فیلتر شده است میباشد و خروجی آغشته به نویز سفید با واریانس و متوسط صفر شده است.
پیاده سازی در Matlab
ابتدا برنامه data.m برای تولید زوج ورودی-خروجیهای سیستم اصلی را نوشتیم. توضیحات این برنامه به صورت زیر است:
N=4998;
تعداد نمونه های مورد نیاز برای زوجهای ورودی-خروجی تعیین میشود
a=[0.25; 0.28];
b=[-0.3; 1];
f=0.05;
d=[0.8; -.5;-.3317];
پارامترهای سیستم مورد نظر تعیین میشوند.
u1=random(‘normal’,0,1,1,N);
ورودی به صورت نویز سفید با واریانس 1 و متوسط 0 تولید میشود.
Hd=filt;
یک فیلتر دیجیتال میان گذر با پاسخ فرکانسی به صورت زیر برای فیلتر کردن نویز تولید میشود. تابع filt با استفاده ار جعبه ابزار طراحی فیلتر، فیلتر مورد نظر را میسازد.
در اینجا فقط بخشی از گزارش آمده است.
نتایج شبیه سازی با متلب :
با اجرای برنامه هابرای L=1000 و L=2000، چهار جدول زیر را در متغیر res خواهیم داشت:
تخمین پارامترها با کمترین مربعات و خطای مربوطه (L=1000)
| 1 | -0.00659 | 0.0005 | -0.35612 | 0.842653 | -0.04111 | 0.474574 | -0.78084 | -0.40629 | 40.72967 |
| 2 | 0.154543 | 0.176225 | -0.32833 | 0.881719 | 0.152848 | 0.662354 | -0.61221 | -0.43184 | 19.71598 |
| 3 | 0.197432 | 0.247887 | -0.31733 | 0.921543 | 0.130958 | 0.712575 | -0.57606 | -0.40049 | 12.51208 |
| 4 | 0.207314 | 0.264988 | -0.31346 | 0.946817 | 0.10301 | 0.749594 | -0.54252 | -0.37918 | 8.0493 |
| 5 | 0.215027 | 0.273288 | -0.30997 | 0.964384 | 0.084515 | 0.775435 | -0.51488 | -0.36551 | 5.093975 |
| 6 | 0.222152 | 0.279542 | -0.30683 | 0.976933 | 0.071305 | 0.79234 | -0.49532 | -0.35617 | 3.337294 |
| 7 | 0.227552 | 0.283808 | -0.30435 | 0.985651 | 0.062306 | 0.803188 | -0.48218 | -0.34985 | 2.635786 |
| 8 | 0.231306 | 0.286534 | -0.30256 | 0.991498 | 0.0564 | 0.810087 | -0.47357 | -0.34568 | 2.598231 |
| 9 | 0.233813 | 0.288249 | -0.30132 | 0.995322 | 0.052602 | 0.814449 | -0.46802 | -0.34298 | 2.774719 |
| 10 | 0.235446 | 0.289324 | -0.30051 | 0.997782 | 0.050188 | 0.817193 | -0.46448 | -0.34126 | 2.956975 |
تخمین پارامترها با کمترین مربعات و خطای مربوطه (L=2000)
| ?1 | ?2 | ?1 | ?2 | ? | ?1 | ?2 | ?3 | ?(%) | |
| 1 | -0.12378 | -0.15659 | -0.37986 | 0.718368 | -0.01946 | 0.224634 | -0.85179 | -0.47328 | 63.32758 |
| 2 | 0.16214 | 0.128481 | -0.3344 | 0.821934 | 0.171885 | 0.527587 | -0.69167 | -0.4932 | 31.05914 |
| 3 | 0.165024 | 0.205151 | -0.33136 | 0.870575 | 0.22273 | 0.589767 | -0.67422 | -0.44453 | 25.7137 |
| 4 | 0.179799 | 0.221803 | -0.33065 | 0.896862 | 0.162889 | 0.654561 | -0.6349 | -0.41042 | 18.71005 |
| 5 | 0.19552 | 0.236471 | -0.32443 | 0.921744 | 0.130853 | 0.709119 | -0.58773 | -0.38952 | 12.94386 |
| 6 | 0.209639 | 0.249532 | -0.31943 | 0.942771 | 0.104242 | 0.746711 | -0.55013 | -0.37387 | 8.538585 |
| 7 | 0.221747 | 0.259759 | -0.31491 | 0.959246 | 0.08364 | 0.772148 | -0.52218 | -0.3621 | 5.35917 |
| 8 | 0.231521 | 0.267292 | -0.31098 | 0.971804 | 0.068458 | 0.78937 | -0.50193 | -0.35349 | 3.24434 |
| 9 | 0.239039 | 0.272656 | -0.30778 | 0.981075 | 0.057619 | 0.801027 | -0.48756 | -0.34733 | 2.169286 |
| 10 | 0.244608 | 0.276397 | -0.30531 | 0.987744 | 0.050042 | 0.80891 | -0.47751 | -0.343 | 2.044393 |
تخمین پارامترها با گرادیان نزولی و خطای مربوطه (L=1000)
| k | ?1 | ?2 | ?1 | ?2 | ? | ?1 | ?2 | ?3 | ?(%) |
| 1 | 0.060423 | -0.46704 | -0.209 | 0.879689 | 0.748747 | 0.017448 | -0.88734 | 0.460787 | 105.7037 |
| 5 | 0.161963 | 0.217067 | -0.30752 | 0.923394 | 0.162982 | 0.67578 | -0.62516 | -0.39051 | 17.05378 |
| 10 | 0.196779 | 0.254839 | -0.31579 | 0.94987 | 0.138575 | 0.719452 | -0.58344 | -0.37681 | 11.50424 |
| 20 | 0.212716 | 0.273908 | -0.30988 | 0.974279 | 0.099798 | 0.773771 | -0.5218 | -0.35917 | 5.429514 |
| 40 | 0.230141 | 0.287089 | -0.30278 | 0.99437 | 0.062726 | 0.809767 | -0.47521 | -0.34418 | 2.60174 |
| 50 | 0.23383 | 0.289045 | -0.30114 | 0.997945 | 0.055127 | 0.815508 | -0.46729 | -0.34144 | 2.823231 |
| 80 | 0.237545 | 0.290725 | -0.29943 | 1.001313 | 0.047502 | 0.820773 | -0.45992 | -0.33883 | 3.255796 |
تخمین پارامترها با گرادیان نزولی و خطای مربوطه (L=2000)
| k | ?1 | ?2 | ?1 | ?2 | ? | ?1 | ?2 | ?3 | ?(%) |
| 1 | 0.229276 | -0.25464 | 0.259441 | 1.122352 | 0.895597 | 0.713679 | 0.693677 | 0.097339 | 114.8429 |
| 5 | 0.299212 | 0.020519 | -0.19999 | 0.938966 | -0.05262 | 0.989968 | -0.01319 | -0.14067 | 42.50849 |
| 10 | 0.34821 | 0.284299 | -0.24011 | 1.058301 | -0.00516 | 0.917718 | -0.28817 | -0.2734 | 19.13994 |
| 20 | 0.301631 | 0.30444 | -0.27697 | 1.043023 | -0.01531 | 0.876599 | -0.37334 | -0.30362 | 12.08278 |
| 40 | 0.271638 | 0.29123 | -0.29252 | 1.015934 | 0.010476 | 0.843966 | -0.42786 | -0.32351 | 6.580074 |
| 50 | 0.26602 | 0.288597 | -0.29525 | 1.010733 | 0.019144 | 0.836839 | -0.43873 | -0.32744 | 5.415227 |
| 80 | 0.259572 | 0.285414 | -0.29829 | 1.004635 | 0.030262 | 0.828073 | -0.45168 | -0.33208 | 4.046975 |
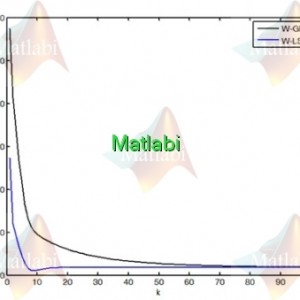
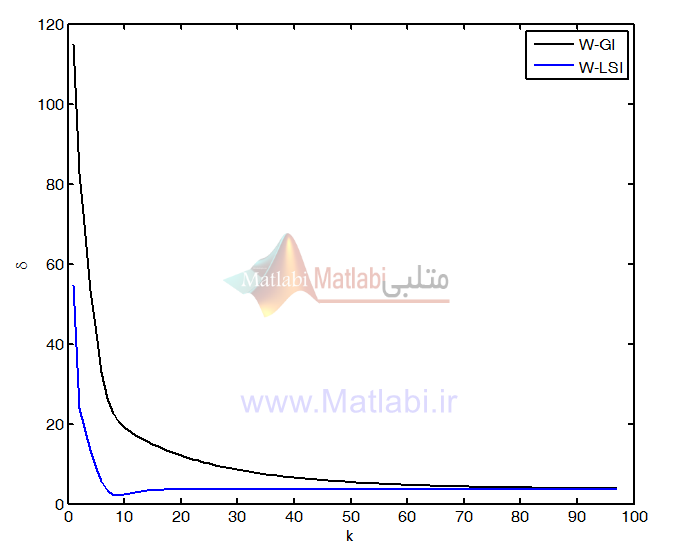
برای مقایسه دو الگوریتم، در برنامه plots.m روند کاهش خطا در هر دو الگوریتم توسط نتایج ذخیره شده درفایلها رسم میشود که با اجرای برنامه شکل زیر قابل مشاهده است:
با توجه به جداول بالا و شکل فوق نتایج زیر را میتوان گرفت:
- خطای هر دو الگوریتم با تکرارهای بیشتر کاهش مییابد
- افزایش طول دادهها درالگوریتم کمترین مربعات خطا را کاهش و در الگوریتم گرادیان نزولی خطا را افزایش داده است.
- الگوریتم کمترین مربعات همگرایی سریعتری نسیت به الگوریتم گرادیان نزولی دارد؛ به طوریکه در اولین تکرارها به مقدر بهینه پارامترها نزدیک میگردد.
- انجام پروژه با قیمت مناسب
نتیجه گیری
دو الگوریتم ارائه شده عملکرد قابل قبولی در شناسایی سیستمهای وینر داشته اند.
روش کمترین مربعات خطا همگرایی سریعتری نسبت به روش گرادیان نزولی دارد، اما نیاز به عملیات معکوس ماتریس گیری دارد.
گرچه ایده این الگوریتم برای سیستمهای وینر داده شده، اما میتوان آن را برای سیستمهای همرشتاین-وینر تعمیم داد.
روشهای کمترین مربعات و گرادیان نزولی مانند روشهای ماکزیمم شباهت عمل میکنند و میتواند برای سیستمهای غیر یکنواخت نمونه برداری شده مورد استفاده قرار گیرد.
دارای 11 صفحه گزارش در قالب ورد است.
برچسب ها:
شناسایی تکراری گرادیانی و کمترین مربعات خطا برای سیستمهای غیر خطی وینر
Signal processing, Least squares, Parameter estimation, Iterative identification, Recursive identification, Stochastic gradient, Wiener nonlinear models, Hammerstein nonlinear models
شبیه سازی مقاله Least squares based and gradient based iterative identification for Wiener nonlinear systems
توسط کارشناسان سایت متلبی تهیه شده است و به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

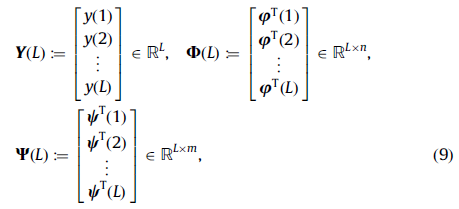
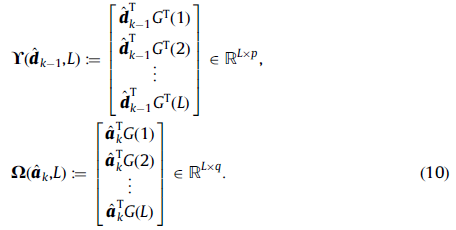

دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.