توضیحات
An autopilot design methodology for bank-to-turn missiles
ترجمه فارسی موضوع مقاله: طراحی اتوپایلوت موشک BTT با کنترل پیش بین تعمیم یافته(GPC)
دارای گزارش 26 صفحه ای در قالب ورد است.
بخشی از گزارش:
معادلات موشک شامل سه معادله نیرو وسه معادله گشتاور است:
معادلات نیرو
… معادلات گشتاور:
شکل 1- پارامترهای مدل موشک
…
زوایه حمله زوایه سرش جانبینرخ رول ، پیچ و یاو ممان اینرسی
معادله (4)(5)(6) به صورت ماتریسی بصورت زیر خواهد بود:
…
- معادلات غیر خطی بدنه:
با صرف نظر از نیروی تراست خواهیم داشت:
…
نیروی وزن بصورت زیر بیان خواهد شد:
…
از (2) و (3) و (11) و (12) رابطه زیر حاصل میشود:
…
زوایای اویلر هستند که برای تبدیل از مختصات بدنی به مختصات مرجع استفاده میشود:
در طول پرواز کوچک خواهند بود در نتیجه:
سرعت کلی موشک به صورت زیر خواهد بود:
از آنجا که سرعت موشک تقریبا ثابت است و بزرگترین جزء سرعت در امتداد محورx است تقریب زیر میتواند در نظر گرفته شود:
در نتیجه:
در نهایت معادله نیرو (25)و (24) بر حسب ضرایب آیرودینامیکی بصورت بیان میشود:
معادله (7) بصورت زیر باز نویسی میشود
معادلات گشتاور بر حسب ضرایب آیرودینامیکی بصورت زیر نیز بیان میشوند:
(32)
بردار حالت به صورت زیر خواهد بود:
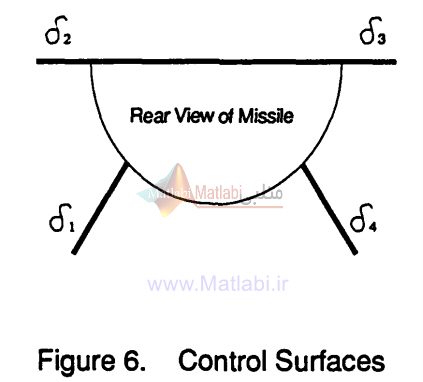
بردار کنترلی δr,δq,δp: به ترتيب زاويه شهپر(Aileron)، بالابر(Elevator)، سکان(Rudder)

بررسی دقیقتر در معادلات (28) تا (33) کوپلینگ اینرسی و آیرودینامیکی نشان میدهد. مدلی که معرفی شد مدلی است که برای طراحی اتوپایلوت استفاده خواهدشد.
برخی از پیش فرضهایی است که میتواند به منظورکاهش منظورمدل مورد استفاده قرارگیرد.
به طوری که دینامیک ها تجزیه شوند بصورت مدل pitch و roll/yaw در اینجا بیان شده اند.
این اطلاعات مربوط به موشک EMRAAT است و معادلات (26) (27) (31) (32) (33) جملاتی ندارند که دینامیکهای Pitch را به roll یا yaw کوپل کنند.
این معادلات نشان می دهد که کوپلینگ بین دینامیکهای roll و yaw وجود دارد. دو مدل ساده شده برای pitch و roll/yaw خواهیم داشت.
معادلات نیرو ابتدا ساده میشوند.
معادله (28) کوپلینگ بین دینامیکهای رول و یاو را به پیچ و معادله (29) کوپلینگ از دینامیکهای پیچ و رول به یاو را نشان می دهد.
برای حذف دینامیکهای roll/yaw از معادله (28) جمله با فرض ناچیز بودن قابل صرف نظر است چون که تقریبا صفر فرض میشود.
برای حذف دینامیکهای pitch از معادله (29) جمله به تغییر میابد چون که یک ثابت است مبتنی بر این فرض که تغییرات آرامی دارد.
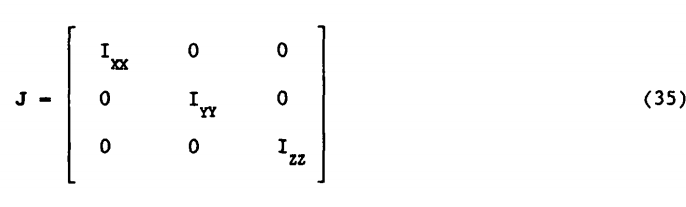
با این فرض که ساختار موشک تقریبا متقارن است ماتریس اینرسی بصورت (35) خواهد بود
این یک روش ممکن برای ساده سازی خواهد بود.
در روشهای دیگر مدل به دینامیکهای roll و pitch/yaw تجزیه میشود.در راهکارهای کلاسیک مدل به دینامیکهای roll,pitch and yaw تجزیه میشوند
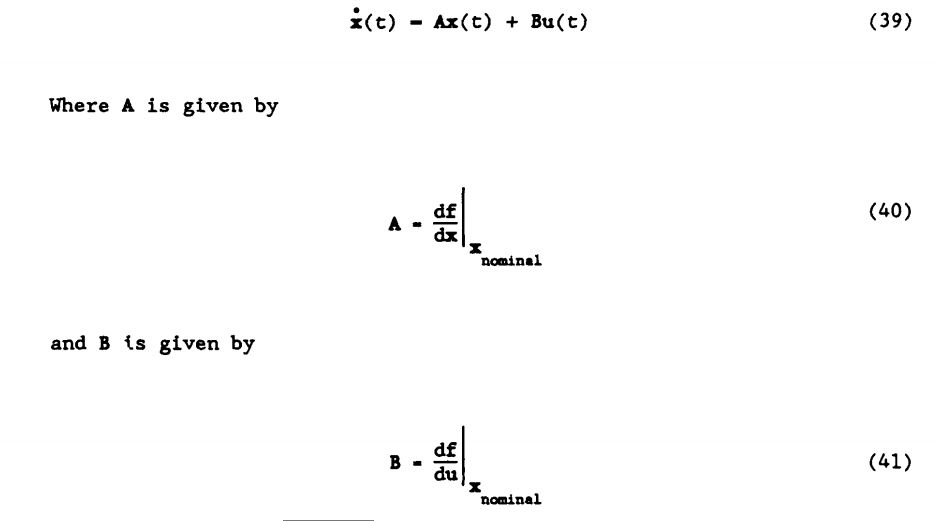
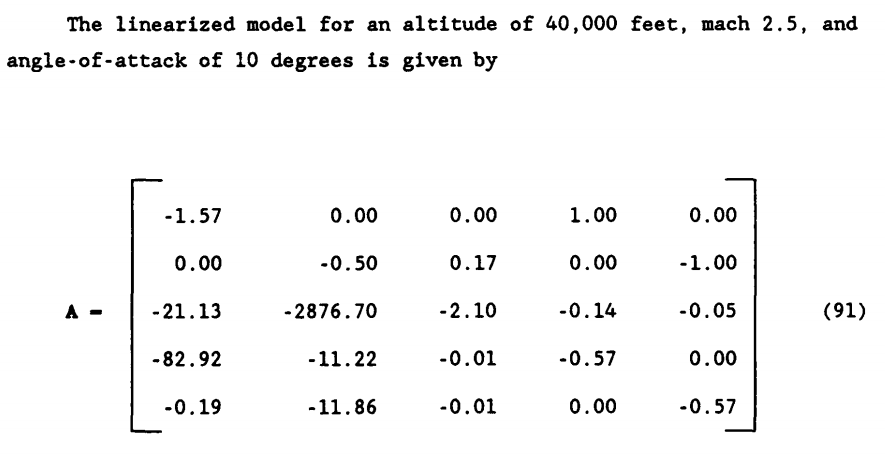
خطی سازی:
با تغییر متغیر زیر معادلات زیر حاصل میشود:
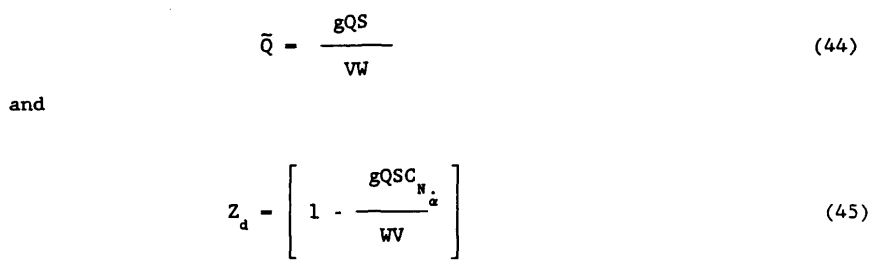
با مشتق رابطه (25) نسبت به داریم:
بدست آوردن ماتریس B
مانند روابط فوق برای معادله(29) تکرار میشود
گام بعدی خطی سازی معادلات گشتاور خواهد بود:
از خطی سازی معادله (62) ماتریسهای M ,N بصورت زیر حاصل میشوند:
با داشتن روابط (9) که H رابیان میکند و (31] و (32) و (33) که I, m, n رابیان میکنند ماتریسهای فوق حاصل میشوند:
و شامل مشتق جزئی معادله (32) خواهند بود:

و در نهایت خواهیم داشت:

ورودی کنترلر میباشد.که از طریق ژیرسکوپ و شتاب سنج در اختیار سیستم کنترل و هدایت قرار می گیرد.
….
شکل 2 – شبیه سازی سیستم غیر خطی
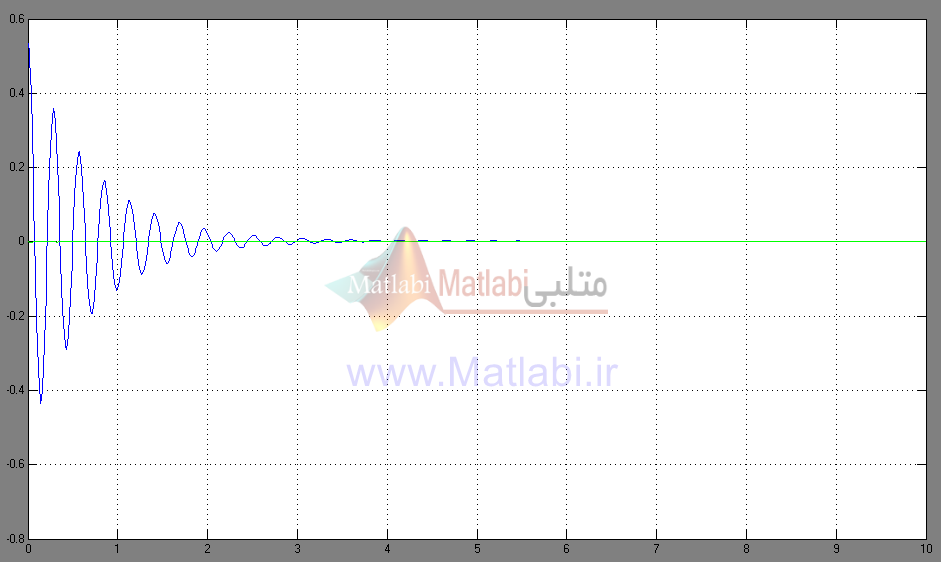
شکل 3 – پاسخ پله خروجی دوم سیستم غیرخطی
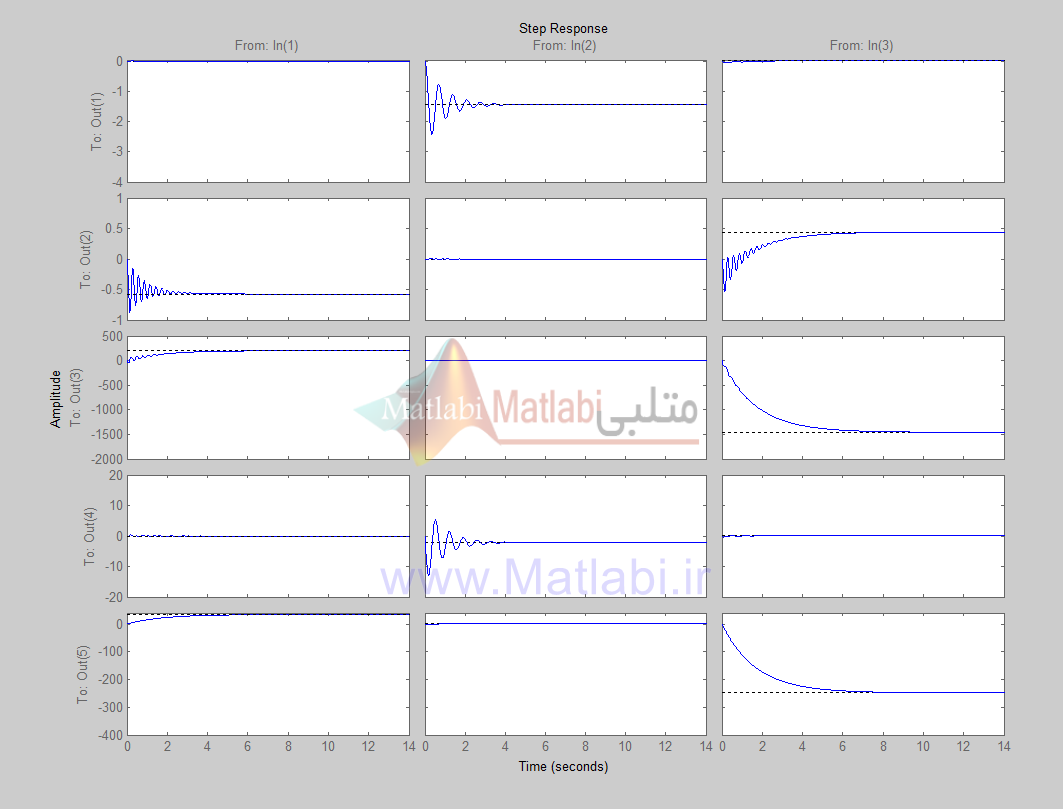
کد شماره 1 جهت تعریف سیستم خطی بکار گرفته شده است. پارامترها با توجه به روند خطی سازی بدست آمده اند . با توجه به وجود 5 حالت در دینامیک سیستم ، پاسخ پله برای 5 خروجی و سه ورودی (ذکر شده در بخش قبل) در شکل 2 به نمایش درآمده است.
کد 1 – تعریف سیستم خطی
شکل 4 – پاسخ پله برای سیستم حلقه باز خطی
با توجه به چند متغیره بودن سیستم ، قبل از طراحی کنترلر سیستم توسط تابع زیر تجزیه حالت می گردد. در واقع خروجی تابع زیر به جای یک سیستم سه خروجی ، سه ورودی سه حلقه تک ورودی تک خروجی مجزا را ارائه می دهد.
تابع Decoupler بعد از تعریف سیستم به صورت کد3 فراخوانی می شود.
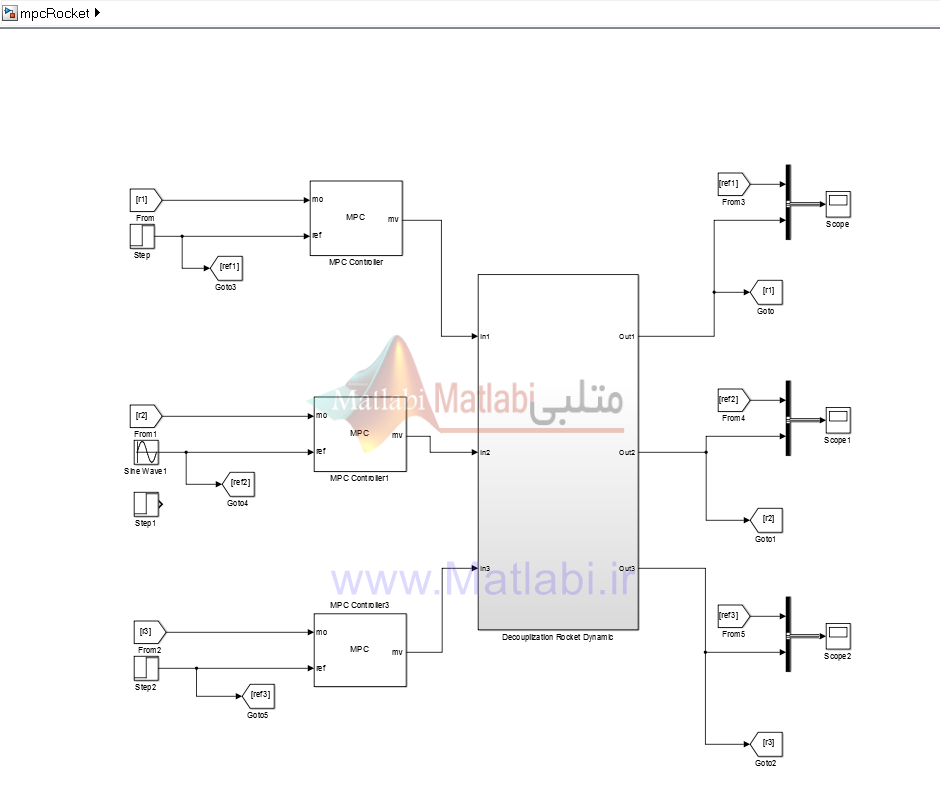
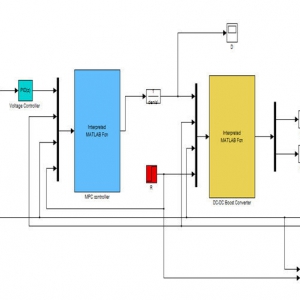
جهت شبیه سازی سیستم در سیمولینک از بلوک Decouplization Rocket Dynamic برای نمایش سیستم و از بلوک MPC مطابق با شکل 5 برای فراخوانی کنترلر استفاده شده است.
همانطور که در شکل مشخص گردیده است برای سه حلقه موجود سه کنترل کننده به صورت مجزا کار می کنند.
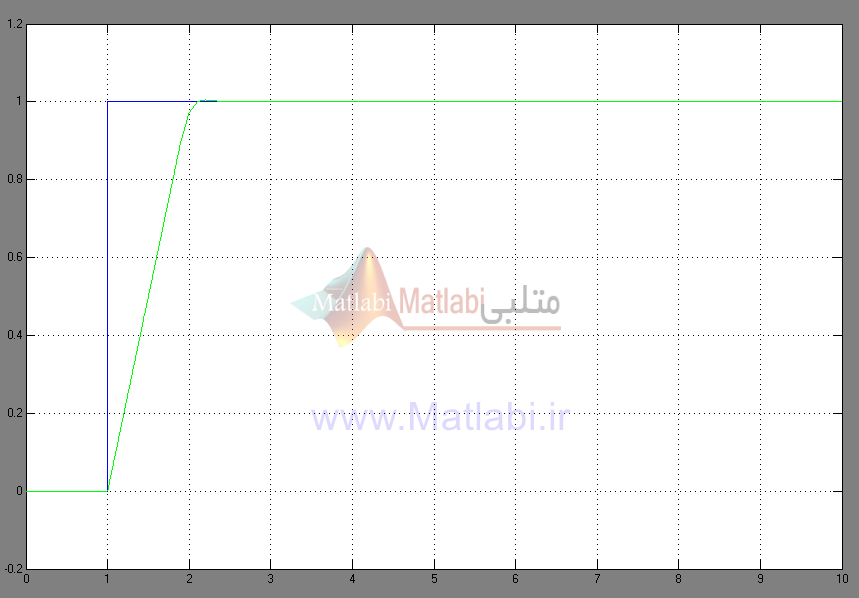
ورودی یک سیگنال پله می باشد و در انتها پاسخ پله سیستم حلقه بسته بدست آمده است. شکل 6 پاسخ تک تک خروجی ها را به ازای ورودی پله نشان می دهد.
همچنین بهره بدست آمده از decoupler به صورت فیدبک در ساختن مدل خطی سیستم بکار رفته است.
در الگوريتم GPC از مدل ARIMAX جهت پيش بيني مقادير خروجي و اغتشاش آينده استفاده مي شود.
اين كنترل كننده داراي عملكرد خوب، فهم راحت، فرموله كردن آسان، كاهش پارامترهاي لازم جهت مدل كردن فرآيند مي باشد و به همين دليل هميشه مورد توجه بوده است.
طراحی کنترل کننده MPC با توجه به توضیحات داده شده و ابزار Matlab در طراحی کنترل کننده های پیش بین در کد شماره 4 انجام گرفته است. فایل ایجاد شده در سیمولینک قابل فراخوانی می باشد.
کد 4 – کنترل کننده MPC
شکل 5 – شبیه سازی سیستم حلقه بسته با کنترل کننده پیش بین
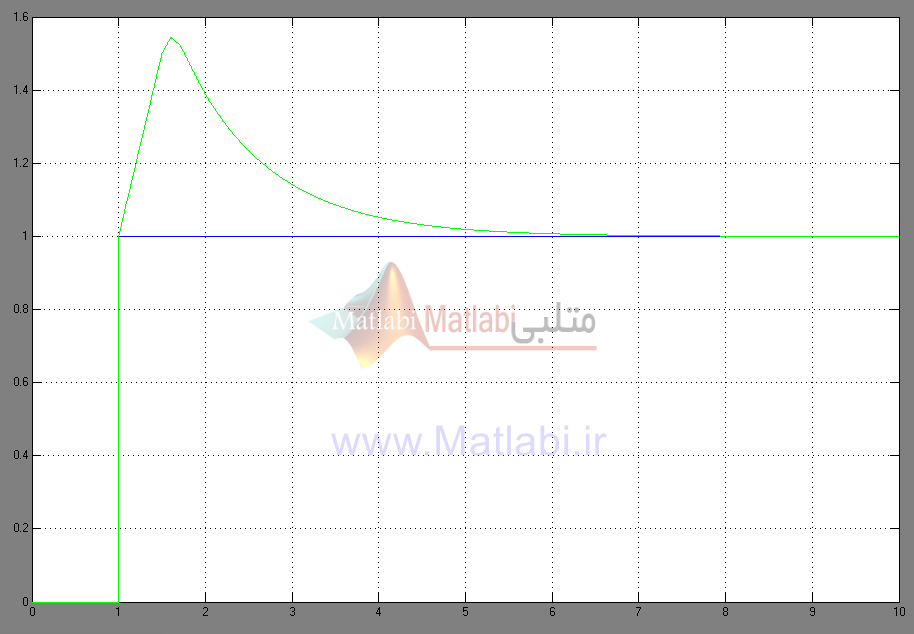
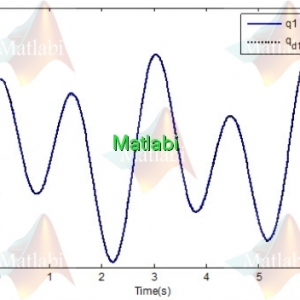
شکل 6 – پاسخ پله خروجی اول با اعمال ورودی اول (α)
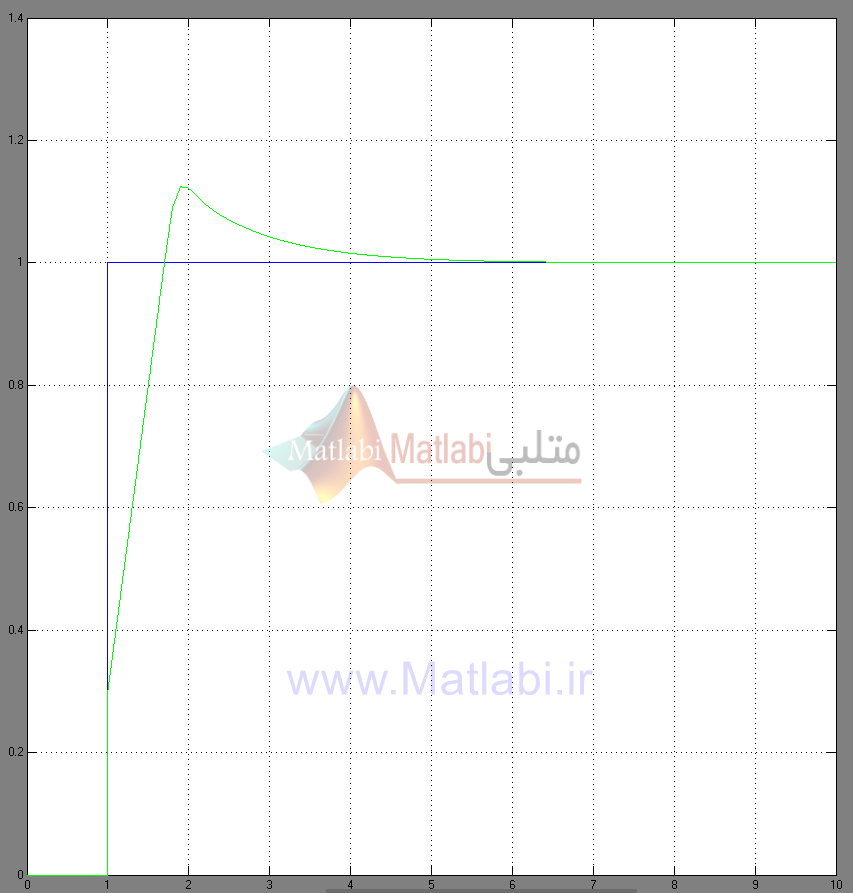
شکل 7 – پاسخ پله خروجی دوم با واعمال ورودی دوم (β)
شکل 8 – خروجی دوم در حضور اغتشاش خروجی (β)
شکل 9 – خروجی سوم در حضور اغتشاش در خروجی (P)
شکل 10- ورودی کنترلی کنترلر پیش بین p)δ(
تعقیب سیگنال حمله:
…
تعقیب سیگنال زاویه سرش جانبی:
…
تغییرات نرخ رول ، پیچ و یاو
…
رسم دستورات کنترلی:
….
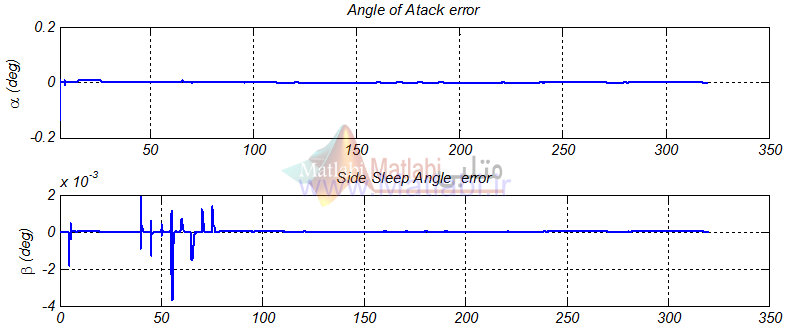
رسم خطا در ردیابی سیگنال
برخورد موشک به هدف:
- بررسی اثر اغتشاش
- بررسی پایداری
شبیه سازی An autopilot design methodology for bank-to-turn missiles
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.

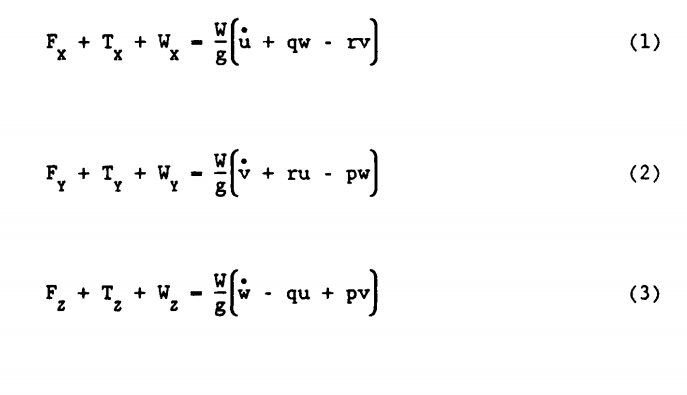
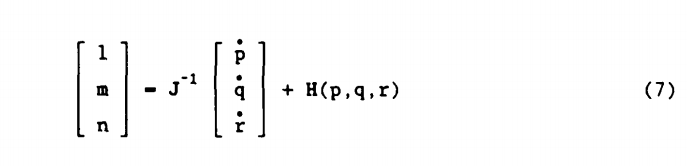
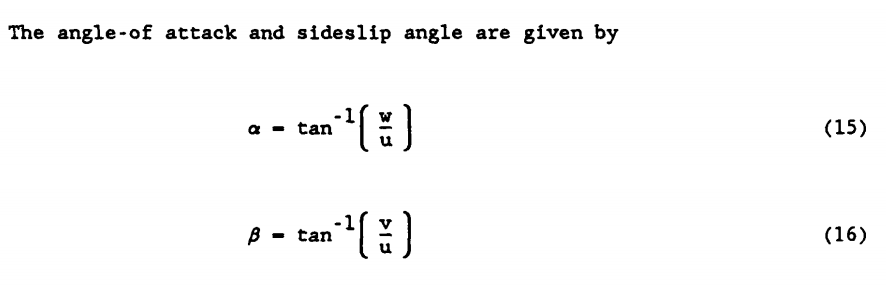





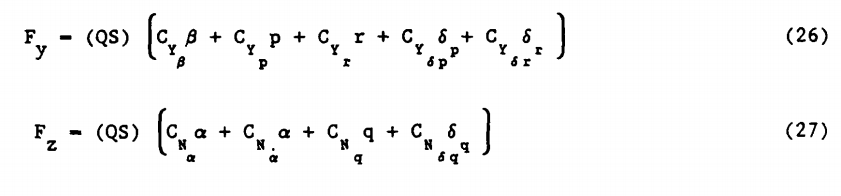
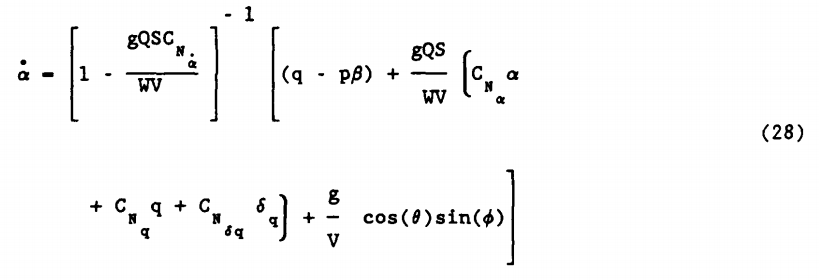

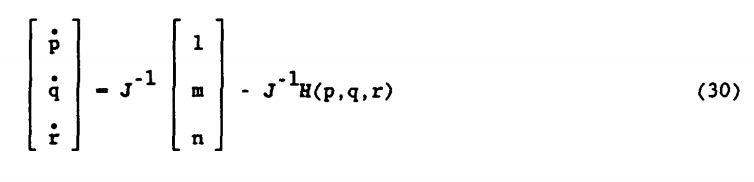
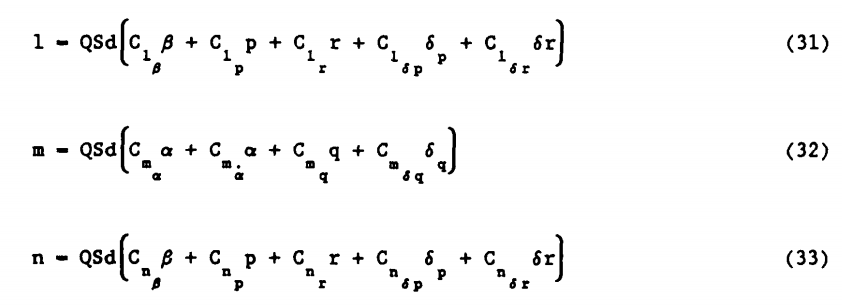
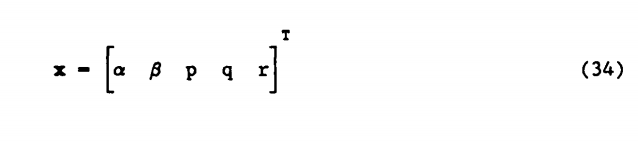



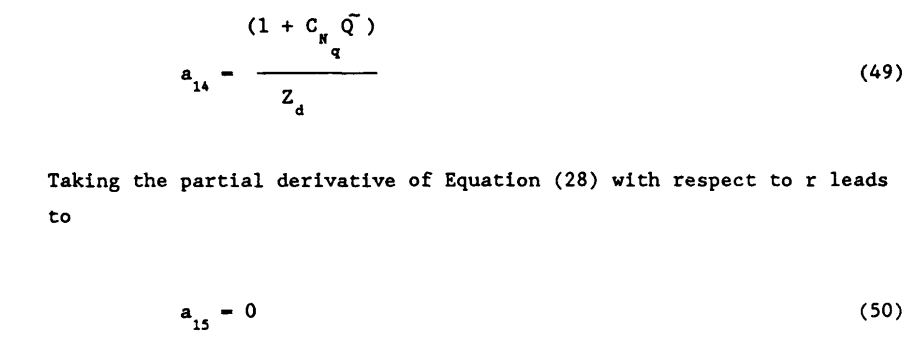

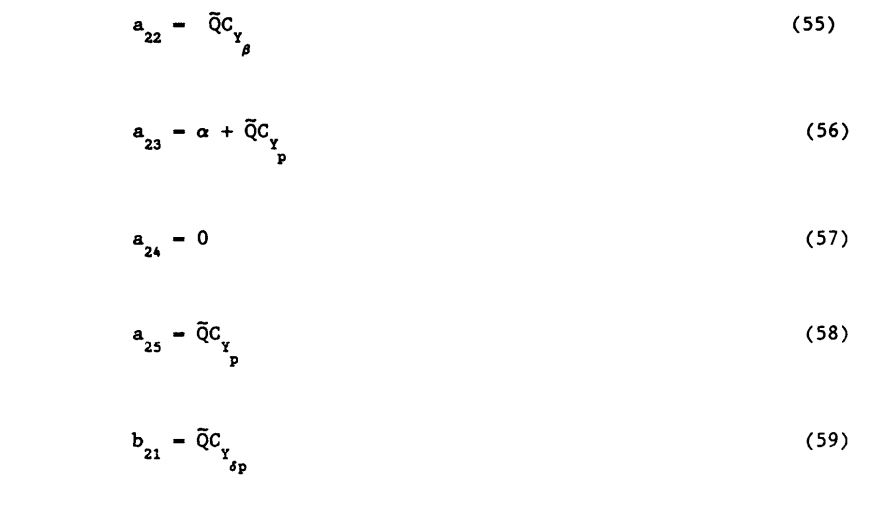



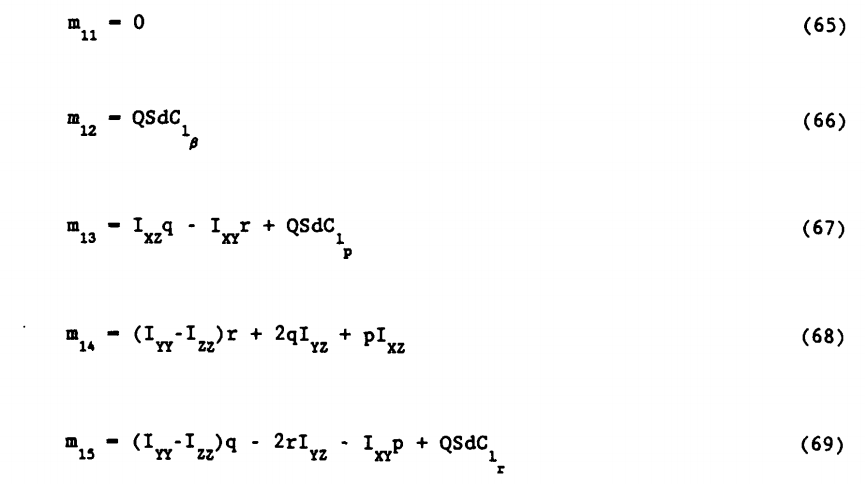







دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.