توضیحات
ایجاد اعداد تصادفی و مقایسه با نمودار چگالی احتمال
موضوع: ایجاد اعداد تصادفی یکنواخت به روش داده گرایی
برای ایجاد اعداد تصادفی یکنواخت از یک حافظه آماده که شامل اعداد تصادفی می باشد استفاده می کنیم
– که باعث افزایش سرعت می شود
– و اعداد تصادفی ایجاد شده کمتر تکراری می باشد
شبیه سازی با 1000 بار تکرار و عمق از 1 تا 10 برای تولید اعداد تصادفی یکنواخت انجام شده است
- یک آرایه شامل اعداد 1 تا 9 و حدوداٌ 100 بارتکرار هر عدد و ترتیب قرار گیری به صورت تصادفی باشد(این آرایه به عنوان حافظه ایجاد اعداد تصادفی می باشد)
- و یک آرایه شامل اعداد 1- (00)با انتخاب این گزینه اعداد داخل حافظه چرخش به چپ
2- (01)با انتخاب این اعداد داخل حافظه جابجایی یک تایی
3- (10)چرخش به راست
4- (11) جابجایی دو تایی
- حال نتایج در آرایه ای به طول 11 که رقم اول ثابت 0.(صفر ممیز) و بقیه بسته به طول ایجاد اعداد تصادفی از 1 تا 10 رقمی ایجاد می شود
ورودی برابر n = که کاربر تعداد تولید ارقام احتمالی بین 1تا10 را انتخاب می کند که n<=10
ورودی دوم برابر m می باشد که در ان کاربر اعمال انجام شده در شمارنده دو بیتی را انتخاب می کند یعنی یا (00) یا (01) یا (10) و یا (11) برای هر عدد کاربر باید دو بار شمارنده انتخاب کند
یعنی اگر طول ارقام تصادفی که انتخاب شده از طرف کاربر 4 باشد 8 بار اعمال (1 تا 4) به طور تصادفی انجام می شود و هر دو بار یک بار یک رقم عدد تصادفی ایجاد شده چاپ می شود
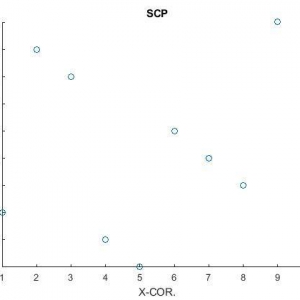
شبیه سازی در محیط متلب و نتایج نموداری باشد که نشان دهد اعداد تولید شده به روش بالا انطباق زیادی با نمودار توزیع یکنواخت دارد.این دو با شبیه سازی مقایسه شود.
اگر تابع چگالی احتمال متغیر تصادفی X به صورت (fX(x) داده شده باشد، میتوان(ولی معمولا غیر ضروری است، زیر را مشاهده کنید) تابع چگالی احتمال متغیری مانند (Y = g(X را محاسبه کرد. به این کار “تغییر متغیر” میگویند و در عمل برای تولید متغیر تصادفی با شکل دلخواه fg(X) = fY با استفاده از مولد عدد تصادفی شناخته شده(برای مثال یکنواخت)، مورد استفاده قرار میگیرد.
اگر تابع g یکنواخت باشد، در آنصورت تابع چگالی حاصل به صورت زیر است:
در اینجا منظور از g−1، تابع معکوس و منظور از ‘g، تابع مشتق است.
این به دنبال این حقیقت ناشی میشود که احتمال در ناحیه مشتق گیری تحت تاثیر تغییر متغیر، باید ثابت بماند. یعنی:
یا
گزارش شبیه سازی با متلب:
دارای 10صفحه گزارش در قالب ورد است.
پروژه تهیه شده حاوی سه فایل MATLAB است. ام فایل برنامه نویسی شده random_gen_m.m و فانکشن random_gen_fun.m مطابق با الگوریتم ارایه شده برنامه نویسی شده و دقیقا مانند هم هستند.
فقط در نحوه دریافت اطلاعات ورودی و چگونگی نمایش اطلاعات خروجی با یکدیگر متفاوت هستند.
ام فایل Test.m هم برای رسم منحنی توزیع نرمال به کار می رود.
ساختار برنامه
ساختار برنامه random_gen_fun.m
همانگونه که در بالا ذکر شد, این فایل, یک فانکشن است و ساختار ورودی-خروجی آن مطابق زیر است.
RANDOM = random_gen_fun(n)
n: تعداد ارقام تصادفی مورد نظر است که کاربر باید وارد کند. n یک صحیح بین 1 و 10 است (مانند 8).
RANDOM: هم برداری است که حاوی اعداد تصادفی ایجاد شده است.
مثال زیر گویای طریقه ی کار با فانکشن random_gen_fun است, که برای تولید 10 عدد تصادفی بین به کار برده شده است.
>> RANDOM = random_gen_fun(10)
RANDOM =
0 4 1 8 7 1 1 7 2 9 1
>>
اطلاعات بیشتر را با خرید این پروژه دریافت نمایید.
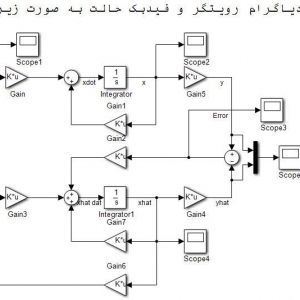
شبیه سازی ایجاد اعداد تصادفی و مقایسه با نمودار چگالی احتمال
به تعداد محدودی قابل فروش می باشد.
سفارش انجام پروژه مشابه
درصورتیکه این محصول دقیقا مطابق خواسته شما نمی باشد،. با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.




دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.